Anti-strong Jamming Polar Coding Optimization Method with Multiobjective Reinforcement Learning
-
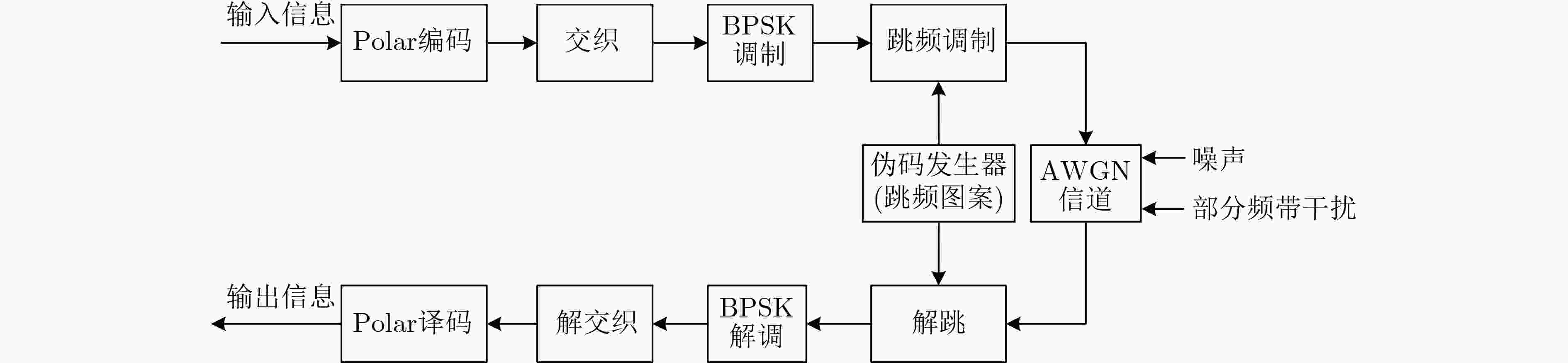
摘要: 为提升跳频(FH)通信系统信息传输的可靠性和抗干扰能力,该文基于新型Polar编码的慢跳频抗干扰通信系统模型,提出一种适应强干扰环境的Polar编码构造优化方法。首先,面向包含常态和干扰态的混合信道设计多目标强化学习算法,然后优化编码过程中的信息位比特信道序列,提升码字的纠错性能,并通过初始化预处理和理论计算回报值降低算法执行复杂度。仿真结果表明,在包含强干扰的混合信道条件下,所提编码优化方法的全局误码性能优于传统编码构造方法,相比于第5代移动通信系统(5G)第3代合作伙伴计划(3GPP) 标准方案全局编码增益达0.5 dB,有效改善Polar编码跳频通信高可靠抗干扰传输性能。Abstract: In order to improve the reliability and anti-jamming ability of information transmission for the Frequency-Hopping (FH) communication system, a Polar coding construction optimization method is proposed to adapt to the strong-jamming environment, which is based on a novel Polar coded slow FH communication system model. Firstly, the multi-objective reinforcement learning algorithm is designed for the hybrid channel containing normal state and jamming state, and then the information bit-channel sequence in the coding process is optimized. Consequently the error correction performance of the designed Polar codewords is improved. In addition, the complexity of algorithm is reduced by preprocessing the initialization and theoretically calculating the reward values. The simulation results show that the overall error performance of the proposed coding optimization method is better than those of conventional coding construction methods in the hybrid channel containing strong jamming. Compared with the 3rd Generation Partnership Project (3GPP) standard scheme in Fifth-Generation (5G) mobile communication systems, the obtained overall coding gain is up to 0.5 dB. Therefore the high-reliability and anti-jamming performance of Polar coded FH transmission is effectively improved.
-
Key words:
- Channel coding /
- Anti-jamming /
- Polar codes /
- Reinforcement learning /
- Reliability performance
-
表 1 初始化预处理后的动作空间占比结果 $ \left| {{\mathbb{T}_{{\mathrm{act}}}}} \right|/K $
N $ {\rho _j} $ 0.1 0.2 0.3 0.4 0.6 256 0.05 0.09 0.12 0.18 0.25 512 0.03 0.05 0.08 0.10 0.16 1024 0.10 0.12 0.15 0.17 0.20 算法1 基于多目标强化学习的Polar编码优化构造算法 (1) 初始化设置Polar码长N, 信息比特长度 K, 干扰因子 $ \{ {\rho _j},1 \le j \le J - 1\} $; (2) 对未干扰接收序列和对应干扰因子 ${\rho _j} $的S个不同干扰样式pi的接收序列,分别重构信息位序列 $ \left\{{\mathcal{A}}_{N}^{\text{GA}},{\mathcal{A}}_{N,1}^{\text{GA}},{\mathcal{A}}_{N,2}^{\text{GA}},\cdots,{\mathcal{A}}_{N,S}^{\text{GA}}\right\} $; (3) 确定初始动作空间 $ {\mathbb{T}}_{{\mathrm{act}}}=\left\{{\mathcal{A}}_{N}^{\text{GA}}\cup {\mathcal{A}}_{N,1}^{\text{GA}}\cup \cdots\cup {\mathcal{A}}_{N,S}^{\text{GA}}\right\}\Bigr\backslash \left\{{\mathcal{A}}_{N}^{\text{GA}}\cap {\mathcal{A}}_{N,1}^{\text{GA}}\cap \cdots\cap {\mathcal{A}}_{N,S}^{\text{GA}}\right\} $,初始状态的信息位序列
$ s:{\mathcal{A}}_{N,in}^{o}=\left\{{\mathcal{A}}_{N}^{\text{GA}}\cap {\mathcal{A}}_{N,1}^{\text{GA}}\cap \cdots\cap {\mathcal{A}}_{N,S}^{\text{GA}}\right\} $;若J > 2,则对每个 ${\rho _j} $获得的 ${\mathcal{A}}_{N,{\mathrm{in}}}^{o} $, ${\mathbb{T}_{{\mathrm{act}}}} $相互间取交集。设周期(episode)数的最大值为E;(4) 随机初始化 $TQ(s,{a^N}) $; (5) 对于每个周期e( $1 \le e \le E $),重复下述(6)~(15)操作; (6) 初始化状态 $s $; (7) 对于每个周期的阶段k,重复下述操作; (8) 选取动作 $a_k^N $,估计误块率值 $ {{\mathrm{bler}}_{j,k}} $,计算回报值 $r_{j,k}^N $,获得 $r_{1,k}^N,r_{2,k}^N,\cdots,s' $; (9) 对于 $ j = 0,1,\cdots,J - 1 $,根据 $r_{1,k}^N,r_{2,k}^N,\cdots,s' $依次计算对应接收序列 ${c_j} $的Q值
${Q_j}(s,{a^N}) = (1 - \alpha ){Q_j}(s,{a^N}) + \alpha ({r_j} + \mathop {\max }\limits_{{a^{N'}}} {Q_j}(s',{a^{N'}})) $;(10) 计算对应接收序列簇 $ c_k^N = \{ {c_0},{c_1},\cdots,{c_{J - 1}}\} $的综合Q值 $TQ(s,{a^N}) $; (11) 基于 $TQ(s,{a^N}) $确定动作 $ a_k^N $; (12) 更新 $\mathcal{A}_{N,k + 1}^o = a_k^N \cup \mathcal{A}_{N,k}^o $, $ {\mathbb{T}_{{\mathrm{act}}}} \leftarrow {\mathbb{T}_{{\mathrm{act}}}}\backslash a_k^N $; (13) 状态转移: $ s \leftarrow s' $; (14) 判断当前状态s是否截止,否,则转到第7步;是,则继续执行下一步; (15) 判断是否满足e=E,否,转到第(5)步;是,继续执行下一步; (16) 输出构造的最优信息位序列 $\mathcal{A}_{N,K}^o $。 表 2 混合信道中所提优化方案与对比方案的全局性能增益差 (dB)
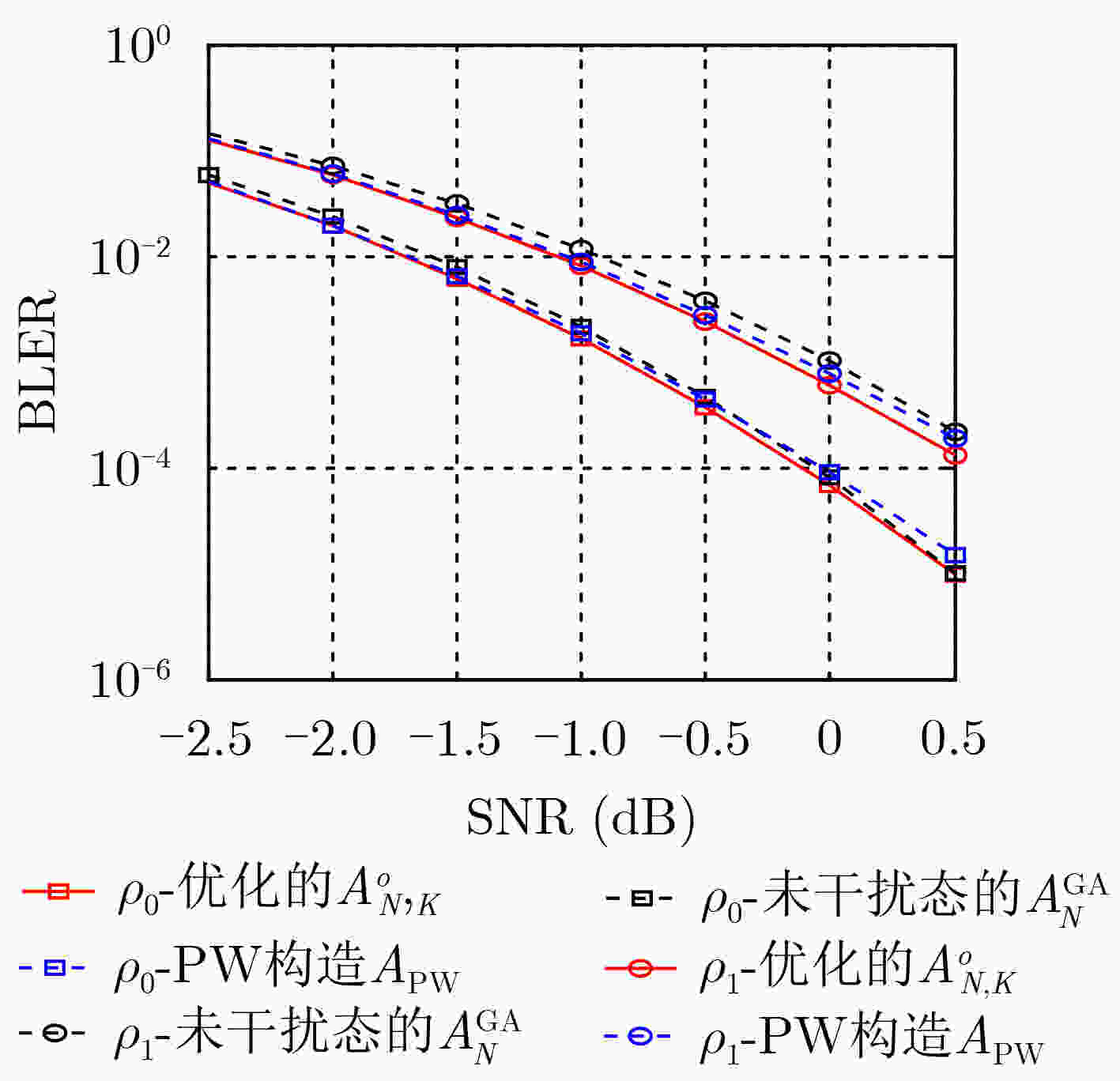
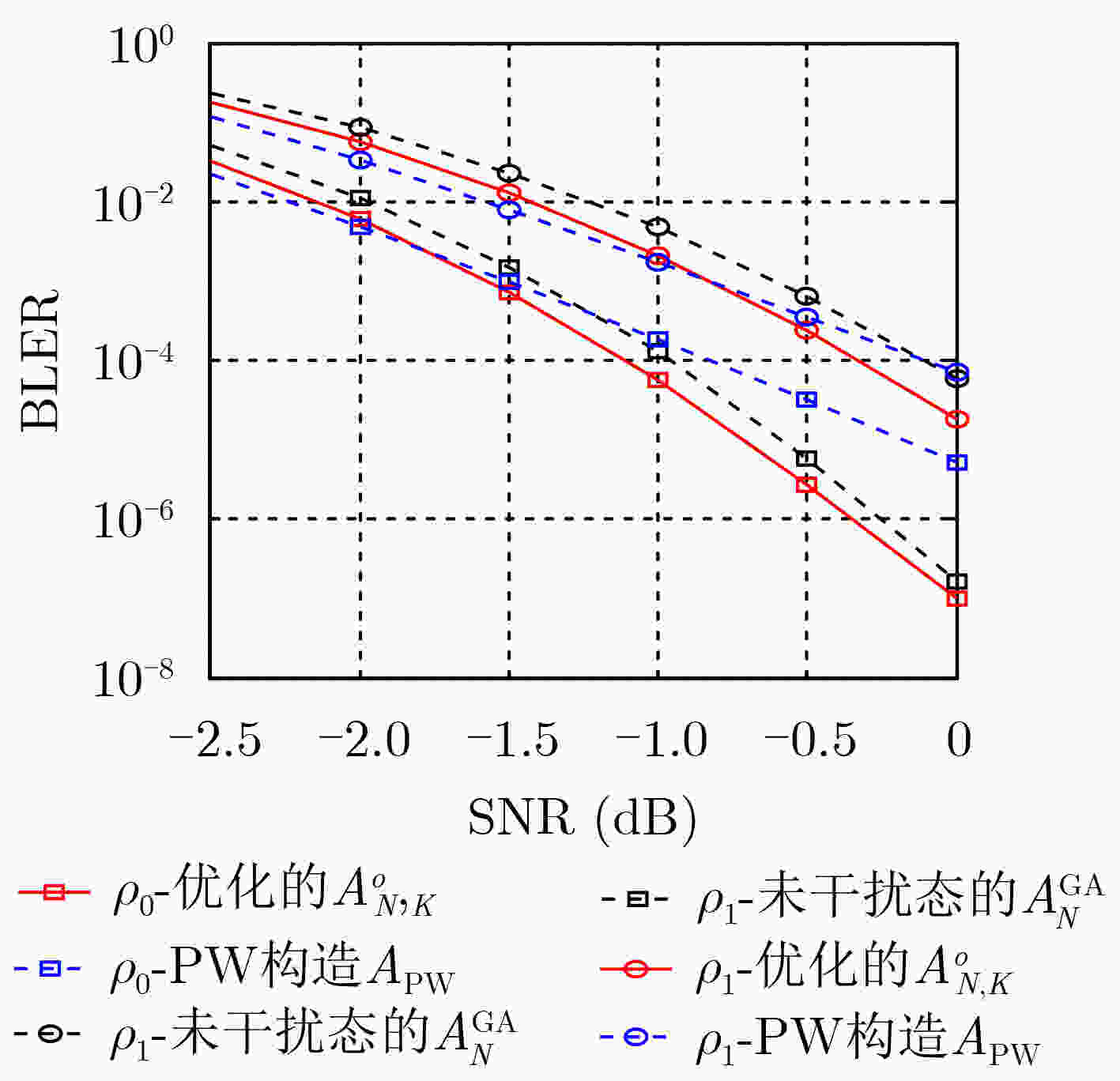
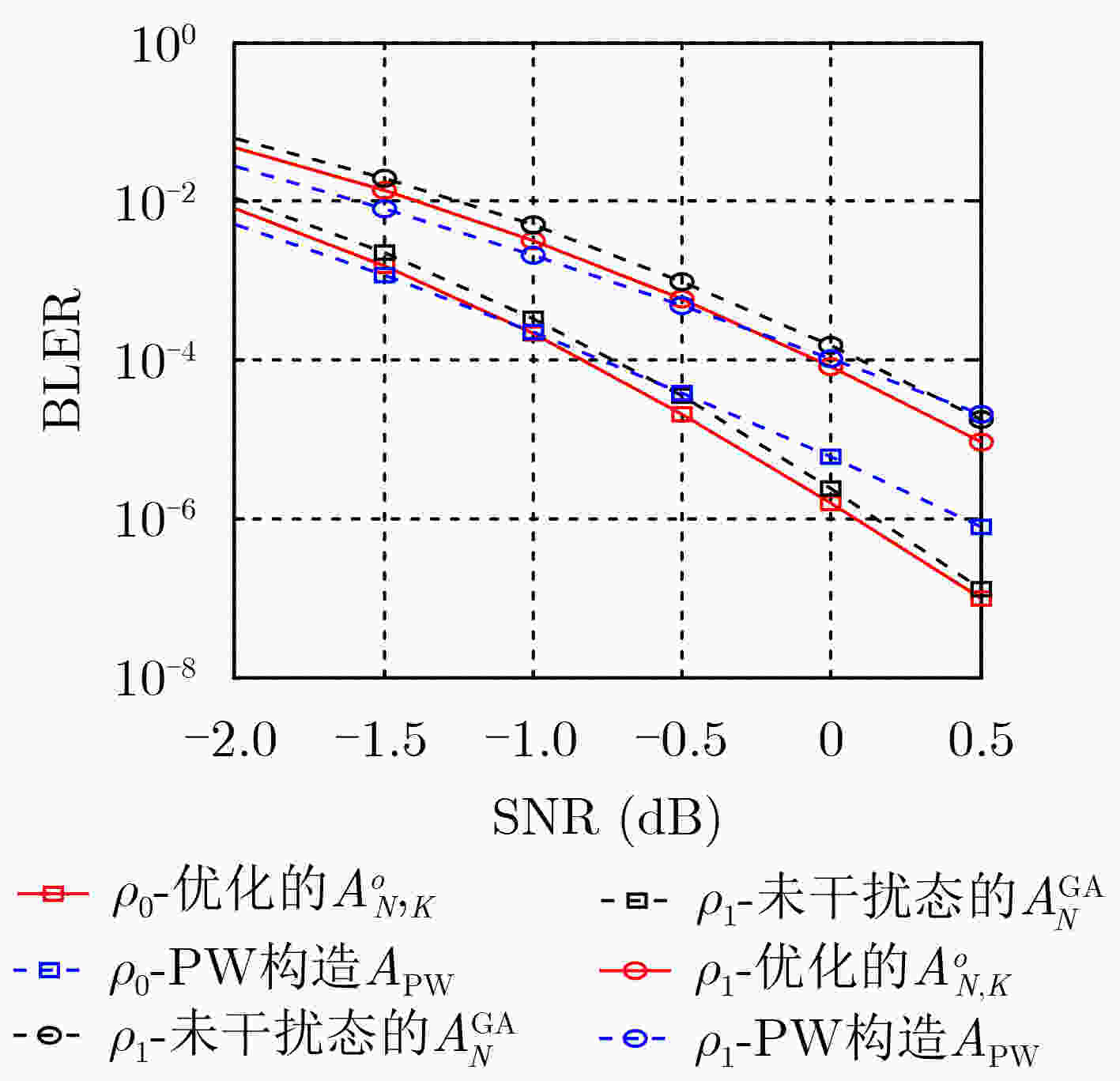
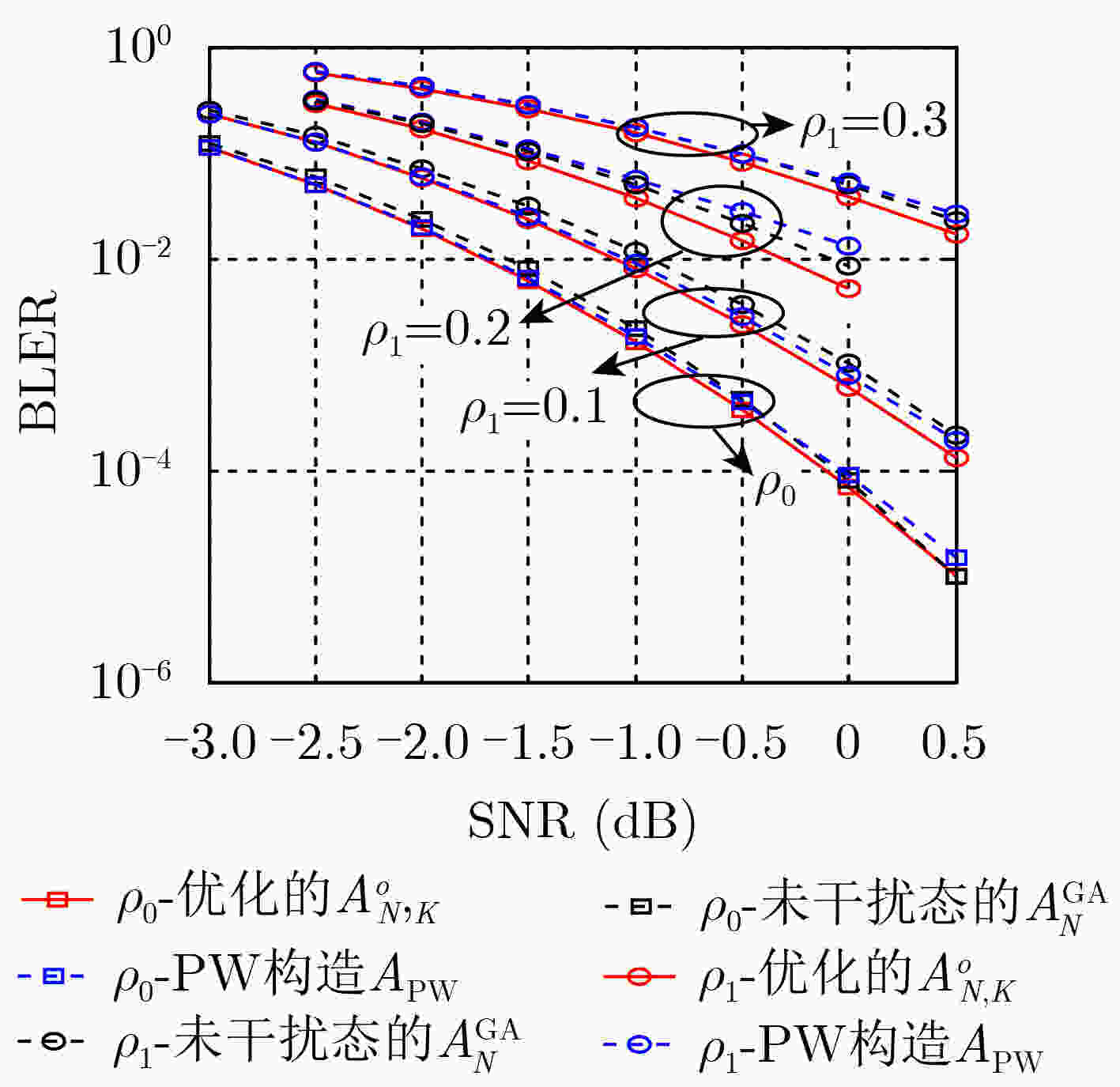
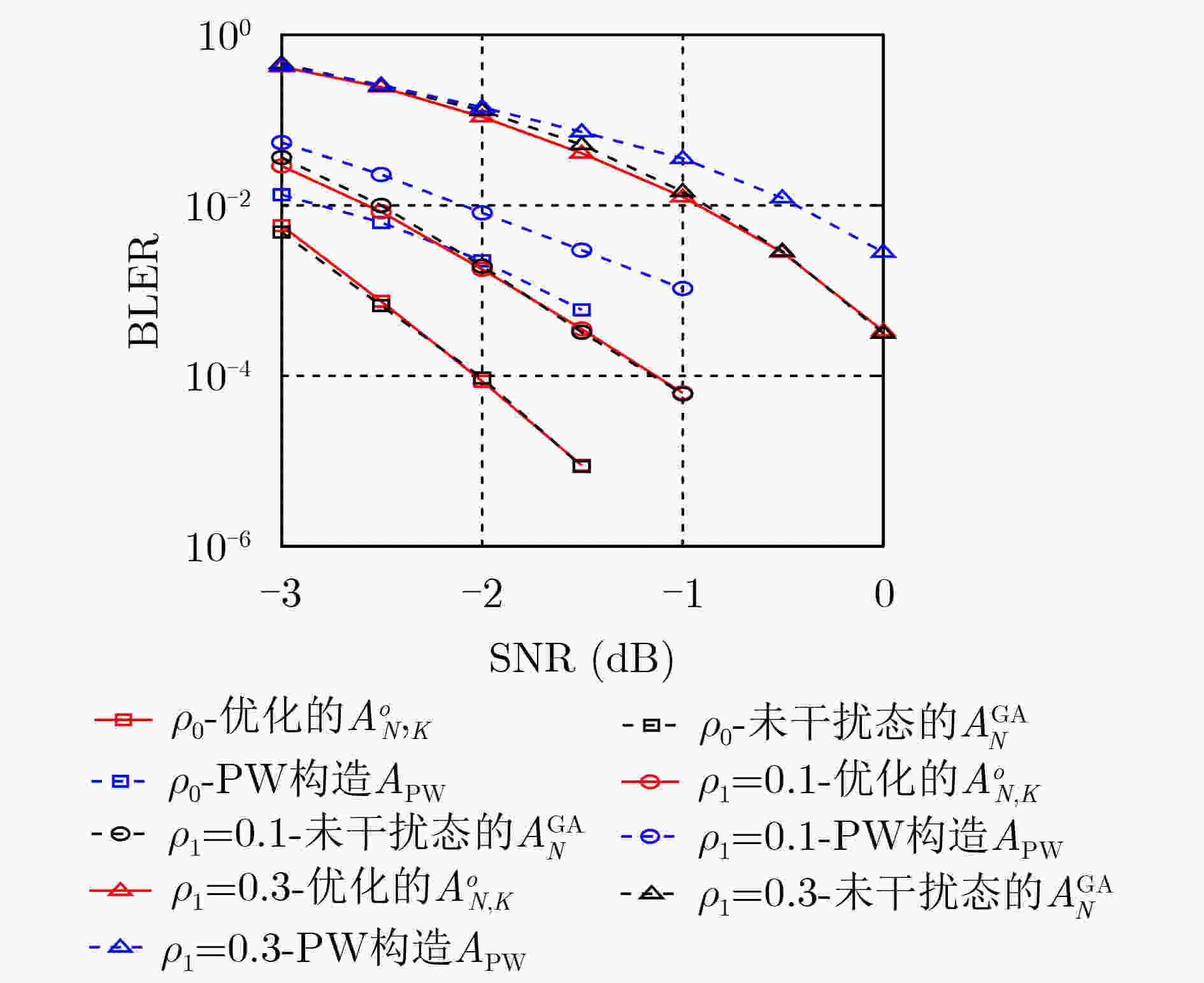
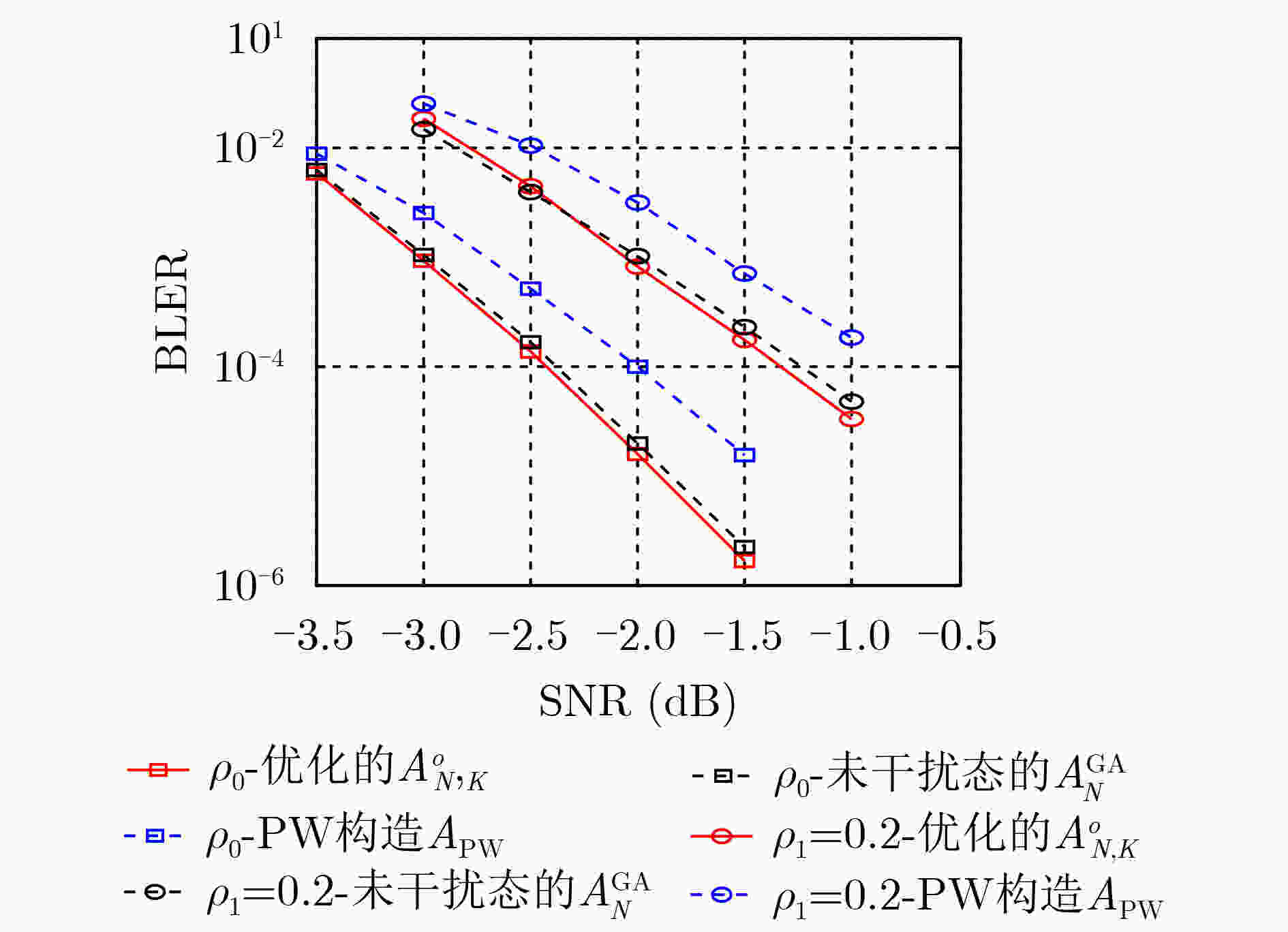
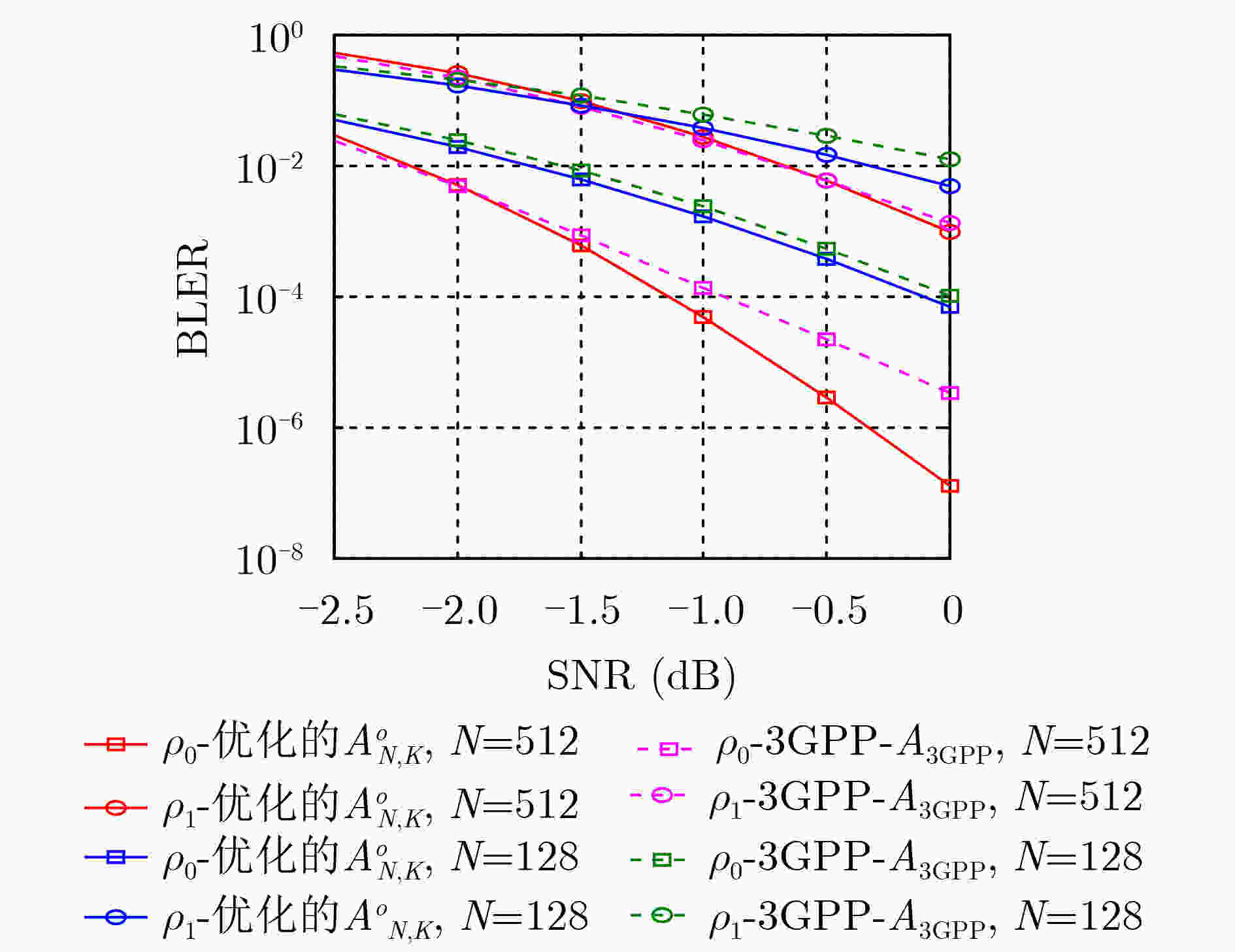
码长N 全局增益差 $ {G_{{\text{dB}}}} $ $ {{\mathrm{BLER}}^{{\text{th}}}} $ $ {10^{ - 2}} $ $ {10^{ - 3}} $ $ {10^{ - 4}} $ 128 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,\mathcal{A}_N^{{\text{GA}}}]}_{{\rho _j}}}} $ 0.27 0.28 0.18 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,{\mathcal{A}^{{\text{PW}}}}]}_{{\rho _j}}}} $ 0.08 0.13 0.27 256 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,\mathcal{A}_N^{{\text{GA}}}]}_{{\rho _j}}}} $ 0.26 0.28 0.26 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,{\mathcal{A}^{{\text{PW}}}}]}_{{\rho _j}}}} $ –0.34 –0.16 0.13 512 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,\mathcal{A}_N^{{\text{GA}}}]}_{{\rho _j}}}} $ 0.32 0.35 0.37 $ \displaystyle\sum\nolimits_j^{J - 1} {{G_{{\text{dB}}}}{{[\mathcal{A}_{N,K}^o,{\mathcal{A}^{{\text{PW}}}}]}_{{\rho _j}}}} $ –0.17 0.08 0.45 -
[1] ARIKAN E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 [2] ETSI. ETSI TS 38 212 V15.2. 0 5G; NR; Multiplexing and channel coding[S]. 2018. [3] NIU Kai, ZHANG Ping, DAI Jincheng, et al. A golden decade of polar codes: From basic principle to 5G applications[J]. China Communications, 2023, 20(2): 94–121. doi: 10.23919/JCC.2023.02.015 [4] 白宝明, 马啸, 陈文, 等. 面向B5G/6G的信息传输与接入技术专题序言[J]. 西安电子科技大学学报, 2020, 47(6): 1–4. doi: 10.19665/j.issn1001-2400.2020.06.001BAI Baoming, MA Xiao, CHEN Wen, et al. Editorial: Introduction to the special issue on information transmission and access technologies for B5G/6G[J]. Journal of Xidian University, 2020, 47(6): 1–4. doi: 10.19665/j.issn1001-2400.2020.06.001 [5] DONG Yanfei, DAI Jincheng, NIU Kai, et al. Joint source-channel coding for 6G communications[J]. China Communications, 2022, 19(3): 101–115. doi: 10.23919/JCC.2022.03.007 [6] 魏浩, 张梦洁, 王东明. 6G极化码低时延译码方案[J]. 移动通信, 2022, 46(6): 64–71. doi: 10.3969/j.issn.1006-1010.2022.06.010WEI Hao, ZHANG Mengjie, and WANG Dongming. Low-latency decoding algorithm of polar codes for 6G wireless systems[J]. Mobile Communications, 2022, 46(6): 64–71. doi: 10.3969/j.issn.1006-1010.2022.06.010 [7] 王任之, 潘克刚, 赵瑞祥. 跳频抗干扰通信系统中LDPC码的编码优化设计[J]. 系统工程与电子技术, 2022, 44(11): 3548–3555. doi: 10.12305/j.issn.1001-506X.2022.11.31WANG Renzhi, PAN Kegang, and ZHAO Ruixiang. Optimal design of LDPC Codes in frequency hopping anti-jamming communication system[J]. Systems Engineering and Electronics, 2022, 44(11): 3548–3555. doi: 10.12305/j.issn.1001-506X.2022.11.31 [8] 孙康宁, 马林华, 茹乐, 等. 混合信道下LDPC码稳定条件分析及度序列优化[J]. 通信学报, 2016, 37(9): 168–174. doi: 10.11959/j.issn.1000-436x.2016188SUN Kangning, MA Linhua, RU Le, et al. Analysis of stability condition for LDPC codes and optimizing degree sequences over mixed channel[J]. Journal on Communications, 2016, 37(9): 168–174. doi: 10.11959/j.issn.1000-436x.2016188 [9] 刘士平, 马林华, 孙康宁, 等. 阻塞式干扰环境下LDPC编码跳频通信优化方案[J]. 火力与指挥控制, 2019, 44(2): 32–36,40. doi: 10.3969/j.issn.1002-0640.2019.02.007LIU Shiping, MA Linhua, SUN Kangning, et al. Optimizing of LDPC coded frequency-hopping communication over blocking interference[J]. Fire Control & Command Control, 2019, 44(2): 32–36,40. doi: 10.3969/j.issn.1002-0640.2019.02.007 [10] MORI R and TANAKA T. Performance of polar codes with the construction using density evolution[J]. IEEE Communications Letters, 2009, 13(7): 519–521. doi: 10.1109/LCOMM.2009.090428 [11] TRIFONOV P. Efficient design and decoding of Polar codes[J]. IEEE Transactions on Communications, 2012, 60(11): 3221–3227. doi: 10.1109/TCOMM.2012.081512.110872 [12] HE Gaoning, BELFIORE J C, LAND I, et al. Beta-expansion: A theoretical framework for fast and recursive construction of Polar codes[C]. Proceedings of 2017 IEEE Global Communications Conference, Singapore, 2017: 1–6. [13] LI Jianxiu and CHENG Wenchi. Stacked denoising autoencoder enhanced Polar codes over Rayleigh fading channels[J]. IEEE Wireless Communications Letters, 2020, 9(3): 354–357. doi: 10.1109/LWC.2019.2954907 [14] LIAO Yun, HASHEMI S A, CIOFFI J M, et al. Construction of polar codes with reinforcement learning[J]. IEEE Transactions on Communications, 2022, 70(1): 185–198. doi: 10.1109/TCOMM.2021.3120274 [15] TENG C F and WU A Y A. Convolutional neural network-aided tree-based bit-flipping framework for polar decoder using imitation learning[J]. IEEE Transactions on Signal Processing, 2021, 69: 300–313. doi: 10.1109/TSP.2020.3040897 [16] LU Yang, ZHAO Mingmin, LEI Ming, et al. Deep learning aided SCL decoding of polar codes with shifted-pruning[J]. China Communications, 2023, 20(1): 153–170. doi: 10.23919/JCC.2023.01.013 [17] KORADA S B and URBANKE R L. Polar codes are optimal for lossy source coding[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1751–1768. doi: 10.1109/TIT.2010.2040961 [18] LIU Chunming, XU Xin, and HU Dewen. Multiobjective reinforcement learning: A comprehensive overview[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45(3): 385–398. -





 下载:
下载:



 下载:
下载:
