Dice系数前向预测的快速正交正则回溯匹配追踪算法

陈平平; 陈家辉; 王宣达; 方毅; 王锋

doi:10.11999/JEIT230558

Dice系数前向预测的快速正交正则回溯匹配追踪算法

doi: 10.11999/JEIT230558

1.
福州大学先进制造学院泉州 362251
2.
广东工业大学信息工程学院广州 510006
3.
泉州师范学院信息工程学院泉州 362200

基金项目: 国家自然科学基金(62171135,62071131)，福建省杰青项目(2022J06010)，省教育厅重点攻关项目(2023XQ004)，泉州市科技计划项目(2021N050)

详细信息

作者简介:
陈平平：男，博士，教授，研究方向为压缩感知、无线通信、信道编码调制、多用户接入

陈家辉：男，硕士生，研究方向为压缩感知、无线通信、多用户接入

王宣达：男，硕士生，研究方向为压缩感知、无线通信、多用户接入

方毅：男，博士，教授，研究方向为信道纠错编码与调制、无线通信

王锋：男，博士，教授，研究方向为电子与通信技术

通讯作者:
方毅　fangyi@gdut.edu.cn

中图分类号: TN911.23
计量
- 文章访问数: 347
- HTML全文浏览量: 240
- PDF下载量: 60
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-10
- 修回日期: 2023-09-22
- 网络出版日期: 2023-10-18
- 刊出日期: 2024-04-24

Regular Backtracking Fast Orthogonal Matching Pursuit Algorithm Based on Dice Coefficient Forward Prediction

1.
School of Advanced Manufacturing, Fuzhou University, Quanzhou 362251, China
2.
School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China
3.
School of Information Engineering, Quanzhou Normal University, Quanzhou 362200, China

Funds: The National Natural Science Foundation of China (62171135, 62071131), Fujian Distinguished Talent Project (2022J06010), The Key Project of Education Department (2023XQ004), Quanzhou Sci-Tech Project (2021N050)

摘要

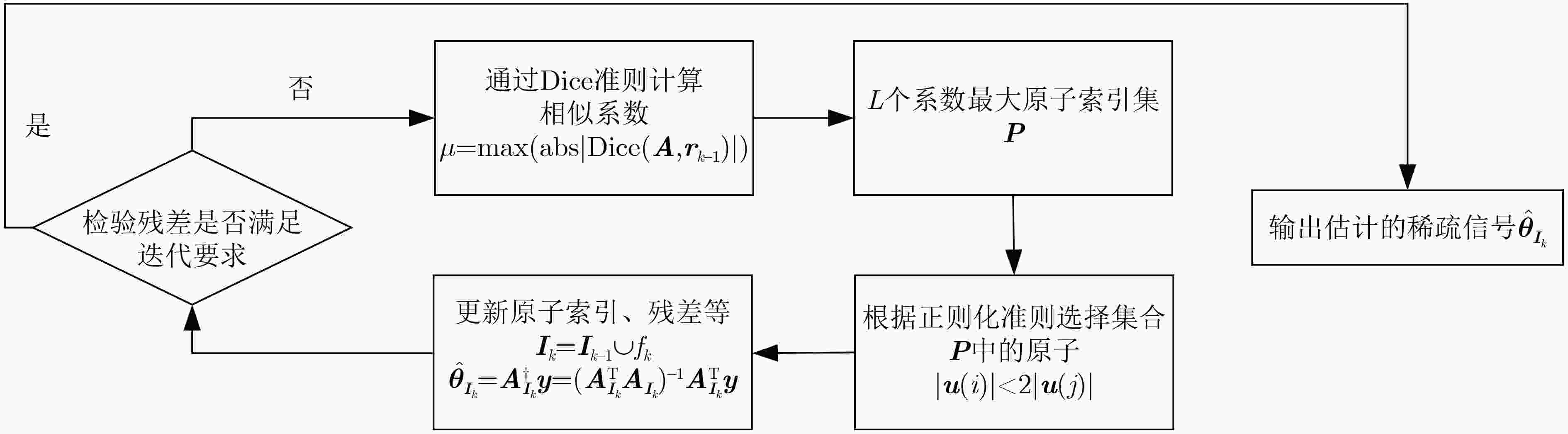
摘要: 为了提高压缩感知重构算法的成功率与重构精度，该文提出基于Dice前向预测的正交正则回溯匹配追踪算法 (DLARBOMP)。在该算法中，首先从匹配准则与预选阶段原子选取的角度，利用Dice系数代替原子内积计算相关度，保留原始信号信息的特性，以此选择与残差最匹配的原子，提高算法的重构精度。同时，针对信号重构过程回溯算法的时间过长问题，在每次原子迭代过程中，该文利用正则化选择多个原子而非单个原子，实现重构精度与重构时间的平衡。最后，通过稀疏1维信号与2维图像信号重构的实验结果，显示了所提DLARBOMP算法在1维信号重构时兼顾了性能与效率，在2维压缩图像信号重构时提高其峰值信噪比(PSNR)，优于正交匹配追踪(OMP)及其最新改进贪婪类算法。
- 信号重构 /
- 压缩感知 /
- Dice系数 /
- 正则回溯 /
- 贪婪类算法
Abstract: In order to improve the success rate and reconstruction accuracy of the compressed sensing reconstruction algorithm, the Look Ahead and Regular Backtracking Orthogonal Matching Pursuit based on Dice coefficient (DLARBOMP) is proposed. In this algorithm, from the perspective of matching criteria and atom selection in the pre-selection stage, the Dice coefficient is used to replace the atomic inner product to calculate the correlation value and preserve the characteristics of the original signal, to select the atom that best matches the residual and improve the reconstruction accuracy. At the same time, to reduce backtracking time in the reconstruction process, regularization is used to select multiple atoms instead of a single atom in each iteration, achieving a balance between reconstruction accuracy and time. Finally, the experimental results of sparse one-dimensional signal and two-dimensional image signal reconstruction show that the proposed DLARBOMP algorithm considers both performance and efficiency when reconstructing one-dimensional signal, and enhances the Peak Signal-to-Noise Ratio (PSNR) when reconstructing two-dimensional compressed image signal, as compared to Orthogonal Matching Pursuit (OMP) and the state-of-the-art greedy algorithms.
- Signal reconstruction /
- Compressed sensing /
- Dice coefficient /
- Regular backtracking /
- Greedy algorithms

HTML全文

图 1 压缩感知过程

下载: 全尺寸图片幻灯片

图 2 DLARBOMP算法流程

下载: 全尺寸图片幻灯片

图 3 N = 256, K = 20, M=80残差值随迭代次数的变化关系

下载: 全尺寸图片幻灯片

图 4 维信号重构实验

下载: 全尺寸图片幻灯片

图 5 重构概率随稀疏度K变化曲线

下载: 全尺寸图片幻灯片

图 6 重构概率随观测次数M变化曲线

下载: 全尺寸图片幻灯片

图 7 重构时间对比

下载: 全尺寸图片幻灯片

图 8 压缩比为0.5时的压缩重构图像

下载: 全尺寸图片幻灯片

表 1 压缩比${M \mathord{\left/ {\vphantom {M N}} \right. } N}$分别为0.3,0.5和0.7时算法重构性能比较

算法	0.3		0.5		0.7
算法	PSNR(dB)	$\sigma $	PSNR(dB)	$\sigma $	PSNR(dB)	$\sigma $
OMP^[10]	20.1031	0.1394	26.3683	0.0902	29.9089	0.0574
LAOMP^[14]	21.9710	0.1377	26.8765	0.0847	30.3367	0.0559
LABOMP^[15]	21.9811	0.1370	27.0628	0.0835	30.3590	0.0554
MMP-IIPMC^[28]	22.0009	0.1318	27.1078	0.0812	31.0811	0.0511
MPSP^[27]	21.9251	0.1301	26.8977	0.0841	30.3806	0.0557
DWBMP^[23]	21.8674	0.1335	26.9524	0.0836	30.3441	0.0552
本文DLARBOMP	22.0072	0.1296	27.2606	0.0810	31.7642	0.0473

下载: 导出CSV

参考文献(30)

[1]	金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2): 470–475. doi: 10.3724/SP.J.1146.2009.00497. JIN Jian, GU Yuantao, and MEI Shunliang. An introduction to compressive sampling and its applications[J]. Journal of Electronics & Information Technology, 2010, 32(2): 470–475. doi: 10.3724/SP.J.1146.2009.00497.
[2]	尹建平, 王志军. 弹药学[M]. 北京: 北京理工大学出版社, 2014: 132–139. YIN Jianping and WANG Zhijun. Ammunition Theory[M]. Beijing: Beijing Institute of Technology Press, 2014: 132–139.
[3]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582.
[4]	CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083.
[5]	CANDÈS E J. Compressive sampling[C]. International Congress of Mathematicians, Madrid, Spain, 2006: 1433–1452.
[6]	HIRSCH L, GONZALEZ M G, and REY VEGA L. A comparative study of time domain compressed sensing techniques for optoacoustic imaging[J]. IEEE Latin America Transactions, 2022, 20(6): 1018–1024. doi: 10.1109/TLA.2022.9757745.
[7]	杨凯. 基于压缩感知的信道估计技术的研究[D]. [硕士论文], 电子科技大学, 2018: 22–23. YANG Kai. Research on channel estimation based on compressed sensing[D]. [Master dissertation], University of Electronic Science and Technology of China, 2018: 22–23.
[8]	DAVE P and JOSHI A. Prediction based method for faster compressive sensing reconstruction using OMP[C]. The 2019 2nd IEEE Middle East and North Africa Communications Conference (MENACOMM), Manama, Bahrain, 2019: 1–4. doi: 10.1109/MENACOMM46666.2019.8988557.
[9]	MALLAT S G and ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082.
[10]	TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108.
[11]	DAI Wei and MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230–2249. doi: 10.1109/TIT.2009.2016006.
[12]	NEEDELL D and VERSHYNIN R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317–334. doi: 10.1007/s10208-008-9031-3.
[13]	NEEDELL D and TROPP J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301–321. doi: 10.1016/j.acha.2008.07.002.
[14]	CHATTERJEE S, SUNDMAN D, and SKOGLUND M. Look ahead orthogonal matching pursuit[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 4024–4027. doi: 10.1109/ICASSP.2011.5947235.
[15]	曾春艳. 匹配追踪的最佳原子选择策略和压缩感知盲稀疏度重建算法改进[D]. [博士论文], 华南理工大学, 2013. ZENG Chunyan. Improvements on optimal atom selection strategies of matching pursuit and blind sparsity reconstruction algorithms in compressed sensing[D]. [Ph. D. dissertation], South China University of Technology, 2013.
[16]	LI Yuanjun and CHEN Wendong. A correlation coefficient sparsity adaptive matching pursuit algorithm[J]. IEEE Signal Processing Letters, 2023, 30: 190–194. doi: 10.1109/LSP.2023.3252469.
[17]	WANG Linyu, YE Pengfei, and XIANG Jianhong. A modified algorithm based on smoothed L0 norm in compressive sensing signal reconstruction[C]. The 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 2018: 1812–1816. doi: 10.1109/ICIP.2018.8451799.
[18]	KILIÇ B, GÜNGÖR A, KALFA M, et al. Sensing matrix design for compressive sensing based direction of arrival estimation[C]. The 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 2020: 1–4. doi: 10.1109/SIU49456.2020.9302073.
[19]	ZEHNG Baifu, ZENG Cao, LI Shidong, et al. Joint sparse recovery for signals of spark-level sparsity and MMV tail-ℓ_{2, 1} minimization[J]. IEEE Signal Processing Letters, 2021, 28: 1130–1134. doi: 10.1109/LSP.2021.3084517.
[20]	ZHONG Xudong, YIN Hao, HE Yuanzhi, et al. Joint downlink power and time-slot allocation for distributed satellite cluster network based on Pareto optimization[J]. IEEE Access, 2017, 5: 25081–25096. doi: 10.1109/ACCESS.2017.2767061.
[21]	CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33–61. doi: 10.1137/S1064827596304010.
[22]	ZHU Mingdong, LI Mingyu, GENG Zhen, et al. Dice coefficient matching-based sparsity adaptive matching pursuit algorithm for the digital predistortion model pruning[C]. The 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 2018: 1032–1035. doi: 10.1109/ICCT.2018.8599901.
[23]	季策, 王金芝, 耿蓉. 基于Dice系数的弱选择回溯匹配追踪算法[J]. 东北大学学报:自然科学版, 2021, 42(2): 189–195. doi: 10.12068/j.issn.1005-3026.2021.02.006. JI Ce, WANG Jinzhi, and GENG Rong. Weak-selection backtracking matching pursuit algorithm based on dice coefficient[J]. Journal of Northeastern University:Natural Science, 2021, 42(2): 189–195. doi: 10.12068/j.issn.1005-3026.2021.02.006.
[24]	刘素娟, 崔程凯, 郑丽丽, 等. 基于压缩感知的贪婪类重构算法原子识别策略综述[J]. 电子与信息学报, 2023, 45(1): 361–370. doi: 10.11999/JEIT211297. LIU Sujuan, CUI Chengkai, ZHENG Lili, et al. A review of atom recognition strategies for greedy class reconstruction algorithms based on compressed sensing[J]. Journal of Electronics & Information Technology, 2023, 45(1): 361–370. doi: 10.11999/JEIT211297.
[25]	刘浩强, 赵洪博, 冯文权. 基于CS的正则化稀疏度变步长自适应匹配追踪算法[J]. 北京航空航天大学学报, 2017, 43(10): 2109–2117. doi: 10.13700/j.bh.1001-5965.2016.0830. LIU Haoqiang, ZHAO Hongbo, and FENG Wenquan. Regularized sparsity variable step-size adaptive matching pursuit algorithm for compressed sensing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2109–2117. doi: 10.13700/j.bh.1001-5965.2016.0830.
[26]	BAIG A, MOINUDDIN A A, and KHAN E. PSNR of highest distortion region: An effective image quality assessment method[C]. 2019 International Conference on Electrical, Electronics and Computer Engineering (UPCON), Aligarh, India, 2019: 1–4. doi: 10.1109/UPCON47278.2019.8980171.
[27]	BLANCHARD J D and TANNER J. Performance comparisons of greedy algorithms in compressed sensing[J]. Numerical Linear Algebra with Applications, 2015, 22(2): 254–282. doi: 10.1002/nla.1948.
[28]	WU Menghang, WU Feiyun, YANG Kunde, et al. A multipath matching pursuit algorithm based on improved-inner product matching criterion[C]. 2020 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Macau, China, 2020: 1–5. doi: 10.1109/ICSPCC50002.2020.9259501.
[29]	焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651–1662. JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Development and prospect of compressive sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651–1662.
[30]	LIU Guangcan, ZHANG Zhao, LIU Qingshan, et al. Robust subspace clustering with compressed data[J]. IEEE Transactions on Image Processing, 2019, 28(10): 5161–5170. doi: 10.1109/TIP.2019.2917857.