A Multi-user Computation Offloading Optimization Model and Algorithm Based on Deep Reinforcement Learning
-
摘要: 在移动边缘计算(MEC)密集部署场景中,边缘服务器负载的不确定性容易造成边缘服务器过载,从而导致计算卸载过程中时延和能耗显著增加。针对该问题,该文提出一种多用户计算卸载优化模型和基于深度确定性策略梯度(DDPG)的计算卸载算法。首先,考虑时延和能耗的均衡优化建立效用函数,以最大化系统效用作为优化目标,将计算卸载问题转化为混合整数非线性规划问题。然后,针对该问题状态空间大、动作空间中离散和连续型变量共存,对DDPG深度强化学习算法进行离散化改进,基于此提出一种多用户计算卸载优化方法。最后,使用该方法求解非线性规划问题。仿真实验结果表明,与已有算法相比,所提方法能有效降低边缘服务器过载概率,并具有很好的稳定性。Abstract: In Mobile Edge Computing (MEC) intensive deployment scenarios, the uncertainty of edge server load can easily cause edge server overload, leading to a significant increase in delay and energy consumption during the computation offloading process. In response to this issue, a multi-user computation offloading optimization model and algorithm based on Deep Deterministic Policy Gradient (DDPG) is proposed. Firstly, considering the balance optimization of delay and energy consumption, a utility function is established to maximize system utility as the optimization objective, and the computational offloading problem is transformed into a mixed integer nonlinear programming problem. Then, in response to the problem of large state space and coexistence of discrete and continuous variables in the action space, the DDPG deep reinforcement learning algorithm is discretized and improved. Based on this, a multi-user computation offloading optimization method is proposed. Finally, this method is used to solve nonlinear programming problems. The simulation experimental results show that compared with existing algorithms, the proposed method can effectively reduce the probability of edge server overload and has good stability.
-
表 1 变量符号及其含义
变量符号 含义 变量符号 含义 ${U_i}$ 用户设备编号 ${P_i}$ ${U_i}$的传输功率 ${M_j}$ MEC服务器编号 ${\sigma ^2}$ 环境高斯白噪声 $t$ 时隙编号 ${v_i}$ ${U_i}$的移动速度 ${f_i}$ ${U_i}$的CPU总频率 ${x_{i,j}}$ ${U_i}$的关联策略 $\varphi $ ${U_i}$的功率系数 $\lambda _i^t$ 任务$\varOmega _i^t$的卸载率 $ D_i^t $ 任务大小 $F_i^t$ ${U_i}$分配到的计算资源 $s$ 单位任务所需计算资源 ${F_{\max }}$ 单个边缘服务器总频率 ${L_j}$ ${M_j}$的工作负载量 算法1 状态归一化算法 输入: Unnormalized variables: ${{\boldsymbol{s}}_t} = ({\boldsymbol{p}}_1^t,\cdots ,{\boldsymbol{p}}_N^t,D_1^t,\cdots ,D_N^t,L_1^t,\cdots ,L_M^t)$, Scale factors: $\rho = ({\rho _x},{\rho _y},{\rho _w},{\rho _l})$ 输出: Normalized variables: $ ({{\boldsymbol{p}}'}_1^t,\cdots ,{{\boldsymbol{p}}'}_N^t,{D'}_1^t,\cdots ,{D'}_N^t,{L'}_1^t,\cdots ,{L'}_M^t) $ (1) ${x'}_i^t = x_i^t*{\rho _x},\forall i$, ${y'}_i^t = y_i^t*{\rho _y},\forall i$, ${D'}_i^t = D_i^t*{\rho _w},\;\forall i$, ${L'}_j^t = L_j^t*{\rho _l},\:\forall j$ //*对状态进行归一化处理 (2) return ${\hat s_t} = ({{\boldsymbol{p}}'}_1^t,\cdots ,{{\boldsymbol{p}}'}_N^t,{D'}_1^t,\cdots ,{D'}_N^t,{L'}_1^t,\cdots ,{L'}_M^t)$ 算法2 动作编码算法 输入: $a$ //*连续动作 输出: ${a_{{\text{dis}}}}$ //*对应的离散编码 (1) ${a_{{\text{num}}}} = K$ (2) ${a_{\min }} = 0,{a_{\max }} = 1$ (3) $ {\varDelta _a} = ({a_{\max }} - {a_{\min }})/({a_{{\text{num}}}} - 1) $ (4) for each $a$ do (5) $a' = \left\lfloor {\dfrac{{a - {a_{\min }}}}{{{\varDelta _a}}}} \right\rfloor $ //*动作编码 (6) ${a_{{\text{dis}}}} = \max (0,\min ({a_{{\text{num}}}} - 1,a'))$ (7) end for (8) return ${a_{{\text{dis}}}}$ 算法3 多用户计算卸载优化方法 输入: Actor learning rate ${\alpha _{{\mathrm{Actor}}}}$, critic learning rate ${\alpha _{{\mathrm{Critic}}}}$, Soft update factor $\tau $. 输出:$a,Q$ //*卸载决策(任务卸载率、分配的计算资源和关联策略),卸载效用 (1) $\mu ({s_t}|{\theta _\mu })$$ \leftarrow $${\theta _\mu }$ and $Q({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}|{\theta _Q})$$ \leftarrow $${\theta _Q}$, ${\theta '_\mu } \leftarrow {\theta _\mu }$ and ${\theta '_Q} \leftarrow {\theta _Q}$ //*初始化主网络和目标网络 Initialize the experience replay buffer ${B_m}$ //*初始化经验重放缓冲区暂存经验元组 (2) for episode=1 to $L$do (3) Initialize system environment (4) for slot=1 to $T$do (5) ${\hat {\boldsymbol{s}}_t} \leftarrow $ SN(${{\boldsymbol{s}}_t},\rho $) //*调用算法1对状态${{\boldsymbol{s}}_t}$预处理 (6) Get the action from equation 式(25) (7) ${{\boldsymbol{a}}'_t} \leftarrow $AE(${{\boldsymbol{a}}_t}$) //*调用算法2离散化动作 (8) perform action ${{\boldsymbol{a}}'_t}$and observer next state ${{\boldsymbol{s}}_{t + 1}}$, Get reward with equation 式(19) (9) ${\hat {\boldsymbol{s}}_{t + 1}} \leftarrow $SN(${{\boldsymbol{s}}_{t + 1}},\rho $) //*调用算法1对状态${{\boldsymbol{s}}_{t + 1}}$预处理 (10) if ${B_m}$is not full then (11) Store transition $({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t},{r_t},{\hat {\boldsymbol{s}}_{t + 1}})$ in replay buffer ${B_m}$ (12) else (13) Randomly sample a mini-batch from ${B_m}$ (14) Calculate target value ${y_t}$ with equation 式(21) (15) Use equation 式(20) to minimize the loss and update the ${\theta _Q}$ (16) Update the ${\theta _\mu }$ by the sampled policy gradient with equation 式(22) (17) Soft update the $ {\theta '_\mu } $ and ${\theta '_Q}$ according to equation 式(23) and 式(24) (18) end if (19) end for (20) Use equation 式(15) to get offloading utility $Q$ (21) end for (22) return $a,Q$ 表 2 仿真参数设置
符号 值 定义 $B$ 40 信道总带宽(MHz) $N$ {5,10,20,30,40} 用户设备数 $K$ 5 MEC服务器个数 ${v_i}$ [0,5] ${U_i}$的移动速度(m/s) ${P_i}$ 100 ${U_i}$的传输功率(mW) ${\sigma ^2}$ –100 环境高斯白噪声(dBm) ${f_i}$ 0.5 ${U_i}$的CPU总频率(GHz) ${F_{\max }}$ 10 单个MEC服务器总频率(GHz) $\varphi $ 10–26 功率系数 $D_i^t$ (1.5,2) 任务$\varOmega _i^t$的大小(Mbit) $s$ 500 所需计算资源(cycle/bit) 表 3 不同${\beta _{\mathrm{t}}}$和${\beta _{\mathrm{e}}}$下的实验结果
${\beta _{\rm t}}$和${\beta _{\rm e}}$的取值 时延(s) 能耗(J) 平均卸载效用 ${\beta _{\rm t}} = 0.1,{\beta _{\rm e}} = 0.9$ 369 394 0.528 ${\beta _{\rm t}} = 0.2,{\beta _{\rm e}} = 0.8$ 343 412 0.534 ${\beta _{\rm t}} = 0.3,{\beta _{\rm e}} = 0.7$ 337 431 0.544 ${\beta _{\rm t}} = 0.4,{\beta _{\rm e}} = 0.6$ 321 441 0.549 ${\beta _{\rm t}} = 0.5,{\beta _{\rm e}} = 0.5$ 308 456 0.554 ${\beta _{\rm t}} = 0.6,{\beta _{\rm e}} = 0.4$ 293 464 0.575 ${\beta _{\rm t}} = 0.7,{\beta _{\rm e}} = 0.3$ 277 479 0.578 ${\beta _{\rm t}} = 0.8,{\beta _{\rm e}} = 0.2$ 256 488 0.613 ${\beta _{\rm t}} = 0.9,{\beta _{\rm e}} = 0.1$ 245 511 0.628 -
[1] ZHOU Zhi, CHEN Xu, LI En, et al. Edge intelligence: Paving the last mile of artificial intelligence with edge computing[J]. Proceedings of the IEEE, 2019, 107(8): 1738–1762. doi: 10.1109/JPROC.2019.2918951. [2] GERARDS M E T, HURINK J L, and KUPER J. On the interplay between global DVFS and scheduling tasks with precedence constraints[J]. IEEE Transactions on Computers, 2015, 64(6): 1742–1754. doi: 10.1109/TC.2014.2345410. [3] SADATDIYNOV K, CUI Laizhong, ZHANG Lei, et al. A review of optimization methods for computation offloading in edge computing networks[J]. Digital Communications and Networks, 2023, 9(2): 450–461. doi: 10.1016/j.dcan.2022.03.003. [4] SUN Jiannan, GU Qing, ZHENG Tao, et al. Joint optimization of computation offloading and task scheduling in vehicular edge computing networks[J]. IEEE Access, 2020, 8: 10466–10477. doi: 10.1109/ACCESS.2020.2965620. [5] LIU Hui, NIU Zhaocheng, DU Junzhao, et al. Genetic algorithm for delay efficient computation offloading in dispersed computing[J]. Ad Hoc Networks, 2023, 142: 103109. doi: 10.1016/j.adhoc.2023.103109. [6] ALAMEDDINE H A, SHARAFEDDINE S, SEBBAH S, et al. Dynamic task offloading and scheduling for low-latency IoT services in multi-access edge computing[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(3): 668–682. doi: 10.1109/JSAC.2019.2894306. [7] BI Suzhi, HUANG Liang, and ZHANG Y J A. Joint optimization of service caching placement and computation offloading in mobile edge computing systems[J]. IEEE Transactions on Wireless Communications, 2020, 19(7): 4947–4963. doi: 10.1109/TWC.2020.2988386. [8] YI Changyan, CAI Jun, and SU Zhou. A multi-user mobile computation offloading and transmission scheduling mechanism for delay-sensitive applications[J]. IEEE Transactions on Mobile Computing, 2020, 19(1): 29–43. doi: 10.1109/TMC.2019.2891736. [9] MITSIS G, TSIROPOULOU E E, and PAPAVASSILIOU S. Price and risk awareness for data offloading decision-making in edge computing systems[J]. IEEE Systems Journal, 2022, 16(4): 6546–6557. doi: 10.1109/JSYST.2022.3188997. [10] ZHANG Kaiyuan, GUI Xiaolin, REN Dewang, et al. Optimal pricing-based computation offloading and resource allocation for blockchain-enabled beyond 5G networks[J]. Computer Networks, 2022, 203: 108674. doi: 10.1016/j.comnet.2021.108674. [11] TONG Zhao, DENG Xin, MEI Jing, et al. Stackelberg game-based task offloading and pricing with computing capacity constraint in mobile edge computing[J]. Journal of Systems Architecture, 2023, 137: 102847. doi: 10.1016/j.sysarc.2023.102847. [12] 张祥俊, 伍卫国, 张弛, 等. 面向移动边缘计算网络的高能效计算卸载算法[J]. 软件学报, 2023, 34(2): 849–867. doi: 10.13328/j.cnki.jos.006417.ZHANG Xiangjun, WU Weiguo, ZHANG Chi, et al. Energy-efficient computing offloading algorithm for mobile edge computing network[J]. Journal of Software, 2023, 34(2): 849–867. doi: 10.13328/j.cnki.jos.006417. [13] YAO Liang, XU Xiaolong, BILAL M, et al. Dynamic edge computation offloading for internet of vehicles with deep reinforcement learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(11): 12991–12999. doi: 10.1109/TITS.2022.3178759. [14] SADIKI A, BENTAHAR J, DSSOULI R, et al. Deep reinforcement learning for the computation offloading in MIMO-based Edge Computing[J]. Ad Hoc Networks, 2023, 141: 103080. doi: 10.1016/j.adhoc.2022.103080. [15] TANG Ming and WONG V W S. Deep reinforcement learning for task offloading in mobile edge computing systems[J]. IEEE Transactions on Mobile Computing, 2022, 21(6): 1985–1997. doi: 10.1109/TMC.2020.3036871. [16] CHENG Nan, LYU Feng, QUAN Wei, et al. Space/aerial-assisted computing offloading for IoT applications: A learning-based approach[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(5): 1117–1129. doi: 10.1109/JSAC.2019.2906789. [17] ZHOU Huan, JIANG Kai, LIU Xuxun, et al. Deep reinforcement learning for energy-efficient computation offloading in mobile-edge computing[J]. IEEE Internet of Things Journal, 2022, 9(2): 1517–1530. doi: 10.1109/JIOT.2021.3091142. [18] WANG Yunpeng, FANG Weiwei, DING Yi, et al. Computation offloading optimization for UAV-assisted mobile edge computing: A deep deterministic policy gradient approach[J]. Wireless Networks, 2021, 27(4): 2991–3006. doi: 10.1007/s11276-021-02632-z. [19] ALE L, ZHANG Ning, FANG Xiaojie, et al. Delay-aware and energy-efficient computation offloading in mobile-edge computing using deep reinforcement learning[J]. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(3): 881–892. doi: 10.1109/TCCN.2021.3066619. [20] DAI Yueyue, XU Du, ZHANG Ke, et al. Deep reinforcement learning for edge computing and resource allocation in 5G beyond[C]. The IEEE 19th International Conference on Communication Technology, Xian, China, 2019: 866–870. doi: 10.1109/ICCT46805.2019.8947146. [21] 3GPP. TR 36.814 v9.0. 0. Further advancements for E-UTRA physical layer aspects[S]. 2010. [22] WANG Yanting, SHENG Min, WANG Xijun, et al. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling[J]. IEEE Transactions on Communications, 2016, 64(10): 4268–4282. doi: 10.1109/TCOMM.2016.2599530. [23] ZHANG Ke, MAO Yuming, LENG Supeng, et al. Energy-efficient offloading for mobile edge computing in 5G heterogeneous networks[J]. IEEE Access, 2016, 4: 5896–5907. doi: 10.1109/ACCESS.2016.2597169. [24] ZHANG Lianhong, ZHOU Wenqi, XIA Junjuan, et al. DQN-based mobile edge computing for smart Internet of vehicle[J]. EURASIP Journal on Advances in Signal Processing, 2022, 2022(1): 45. doi: 10.1186/s13634-022-00876-1. [25] WANG Jin, HU Jia, MIN Geyong, et al. Dependent task offloading for edge computing based on deep reinforcement learning[J]. IEEE Transactions on Computers, 2022, 71(10): 2449–2461. doi: 10.1109/TC.2021.3131040. [26] SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. 2nd ed. Cambridge: A Bradford Book, 2018: 47–50. [27] LIU Y C and HUANG Chiyu. DDPG-based adaptive robust tracking control for aerial manipulators with decoupling approach[J]. IEEE Transactions on Cybernetics, 2022, 52(8): 8258–8271. doi: 10.1109/TCYB.2021.3049555. [28] HU Shihong and LI Guanghui. Dynamic request scheduling optimization in mobile edge computing for IoT applications[J]. IEEE Internet of Things Journal, 2020, 7(2): 1426–1437. doi: 10.1109/JIOT.2019.2955311. -





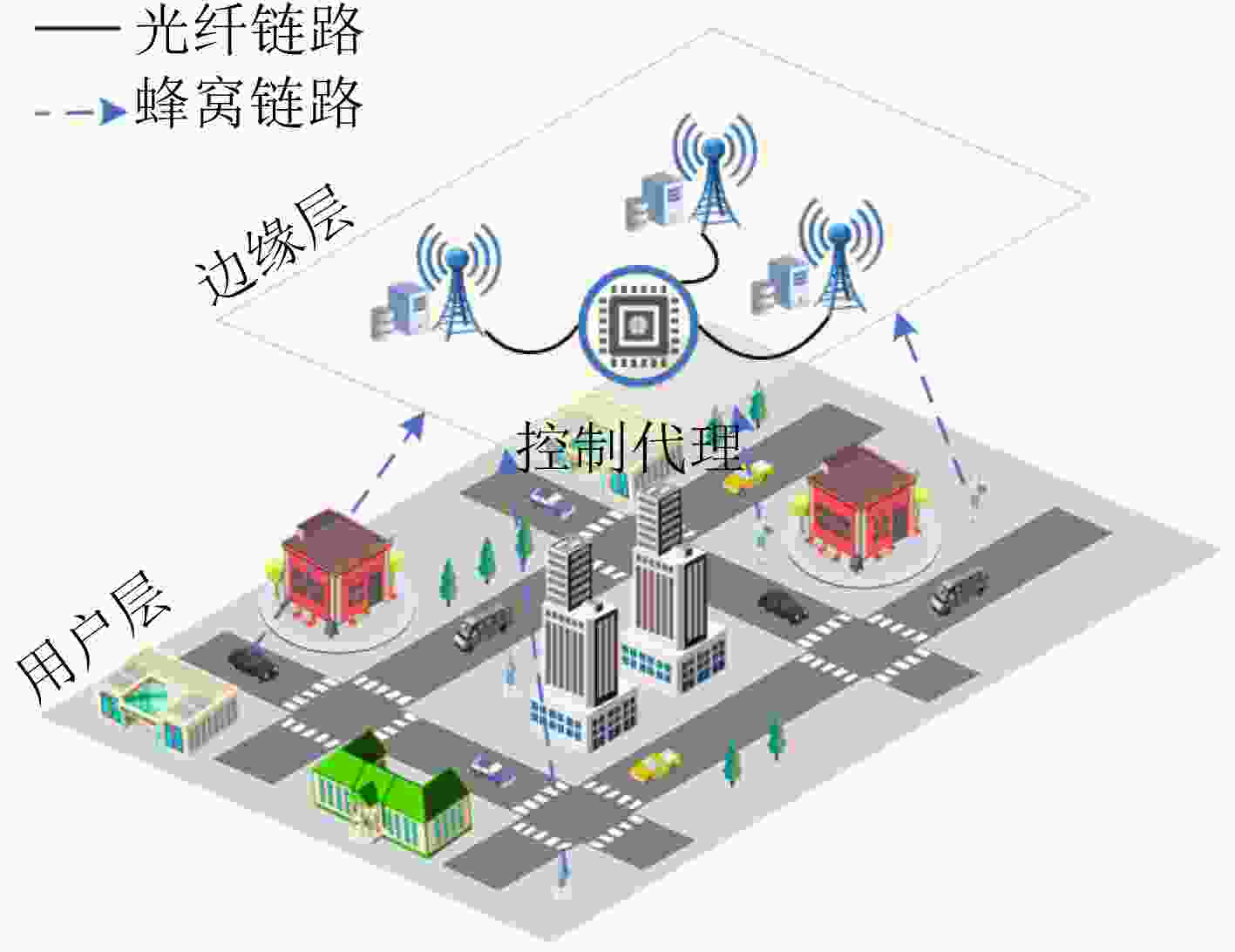
 下载:
下载:
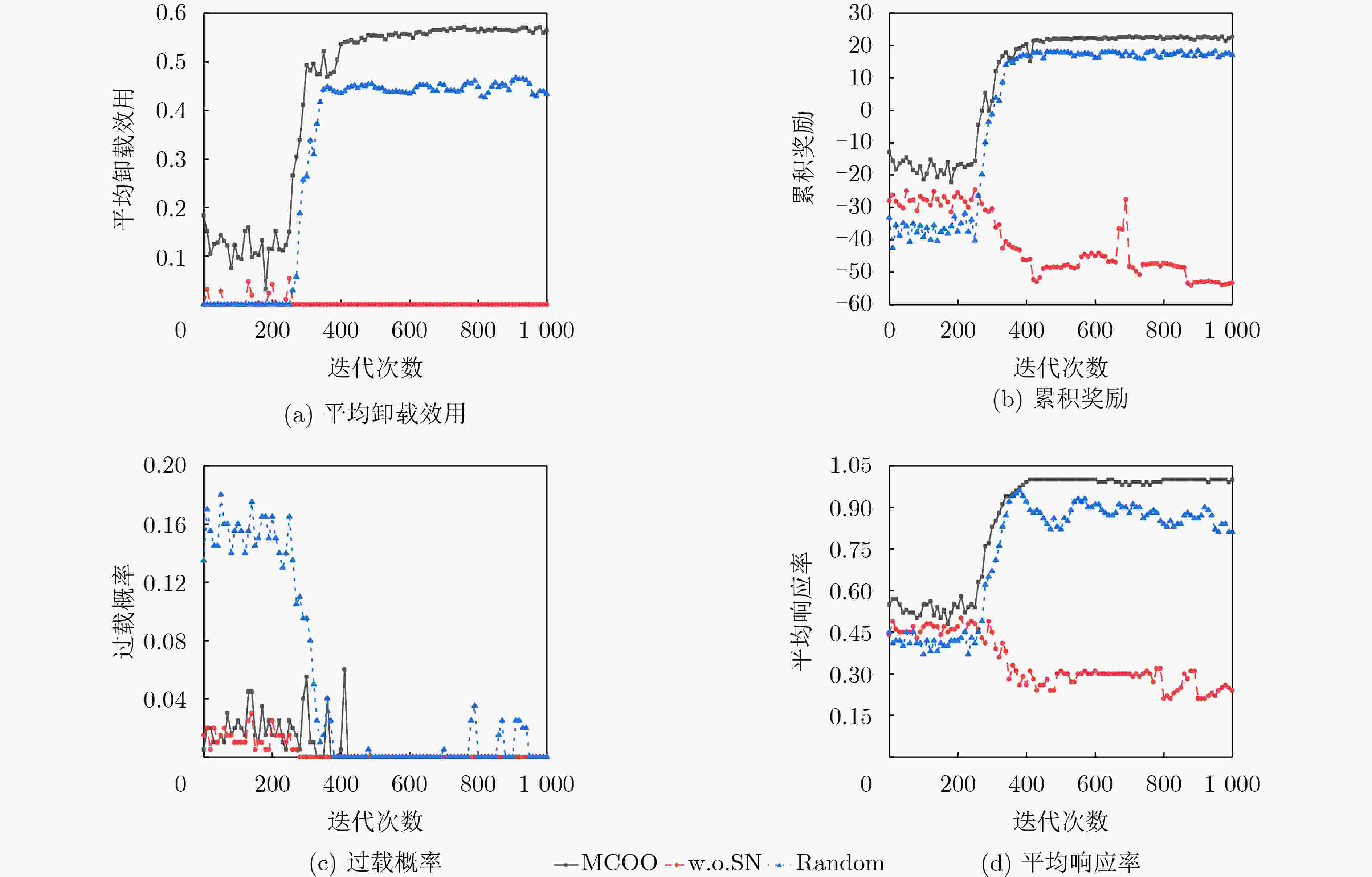
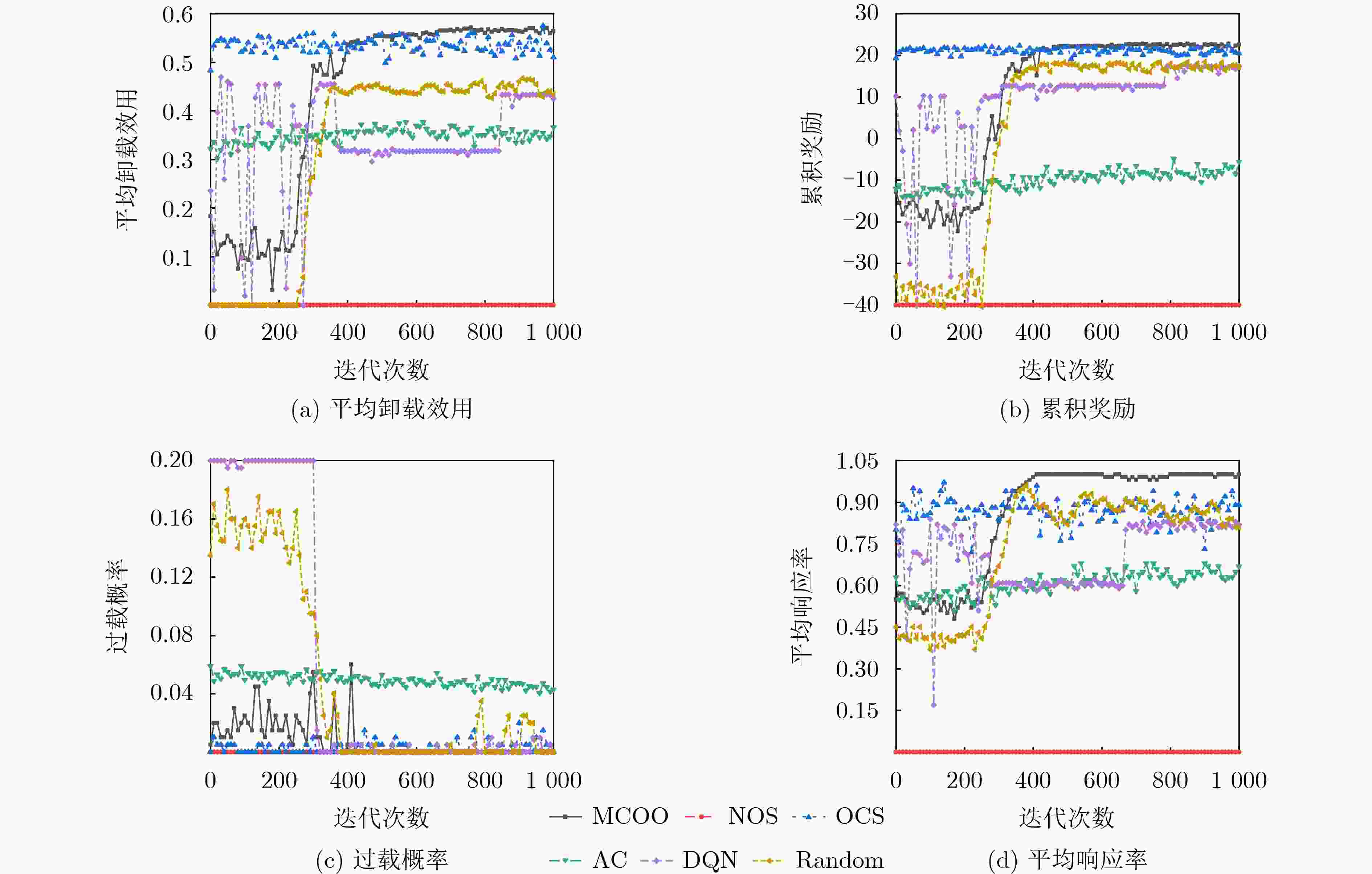
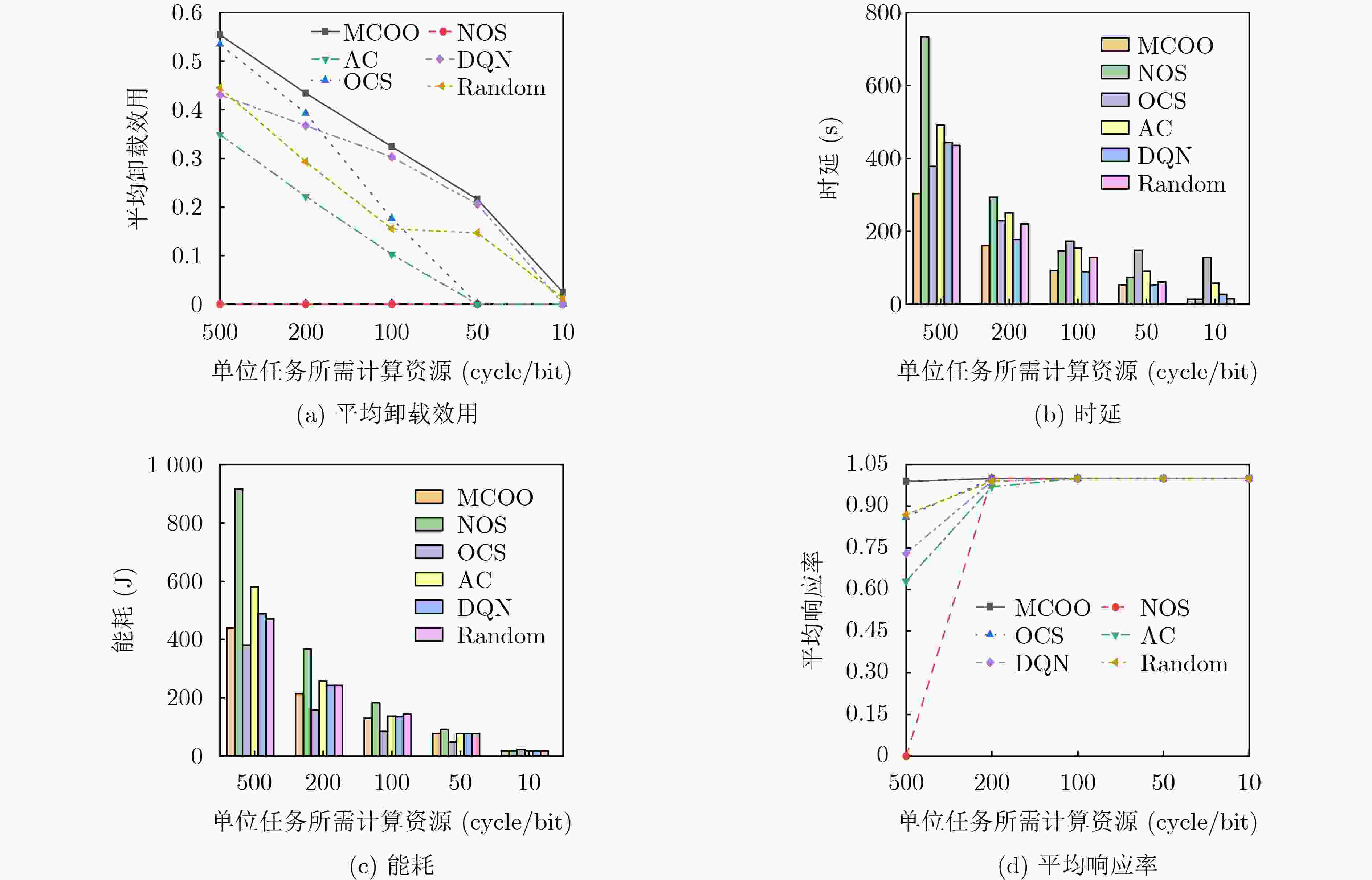
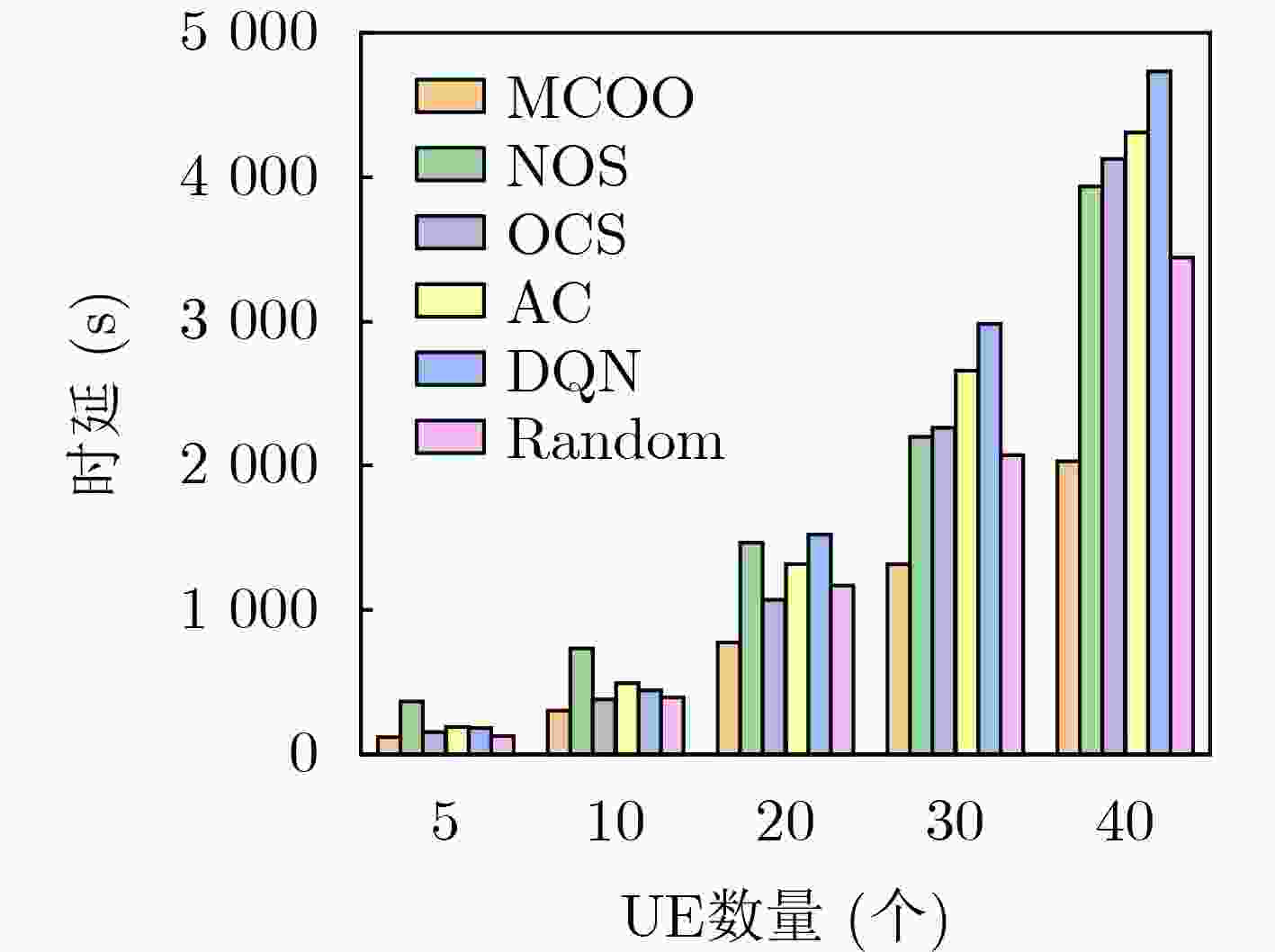
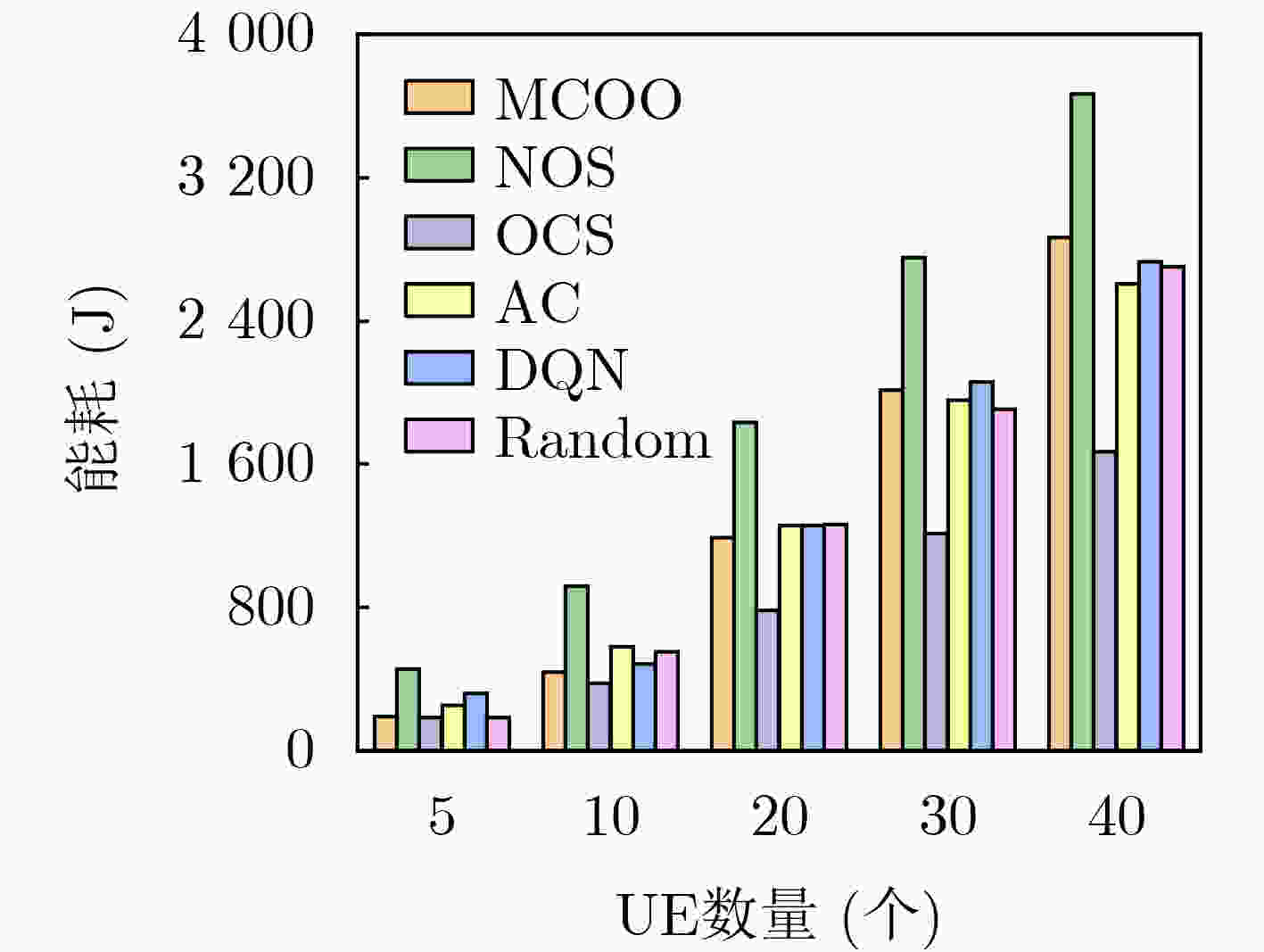
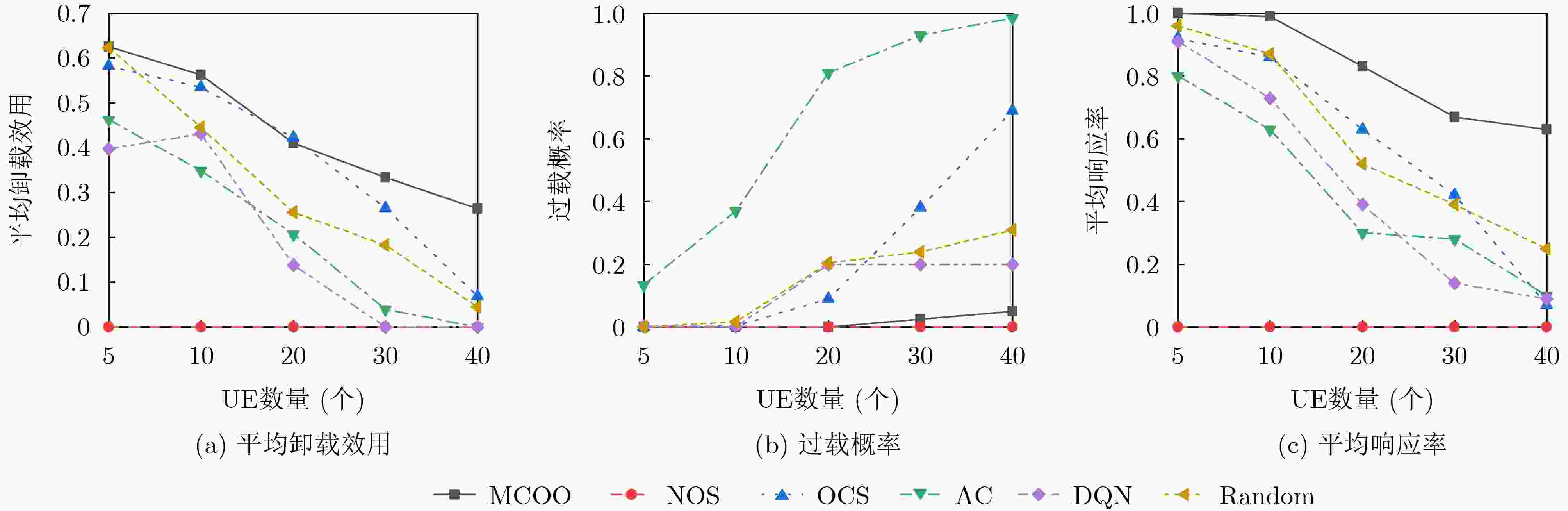


 下载:
下载:
