Angle-only Maneuvering Target Tracking Using Primal-dual Gaussian Particle Filtering
-
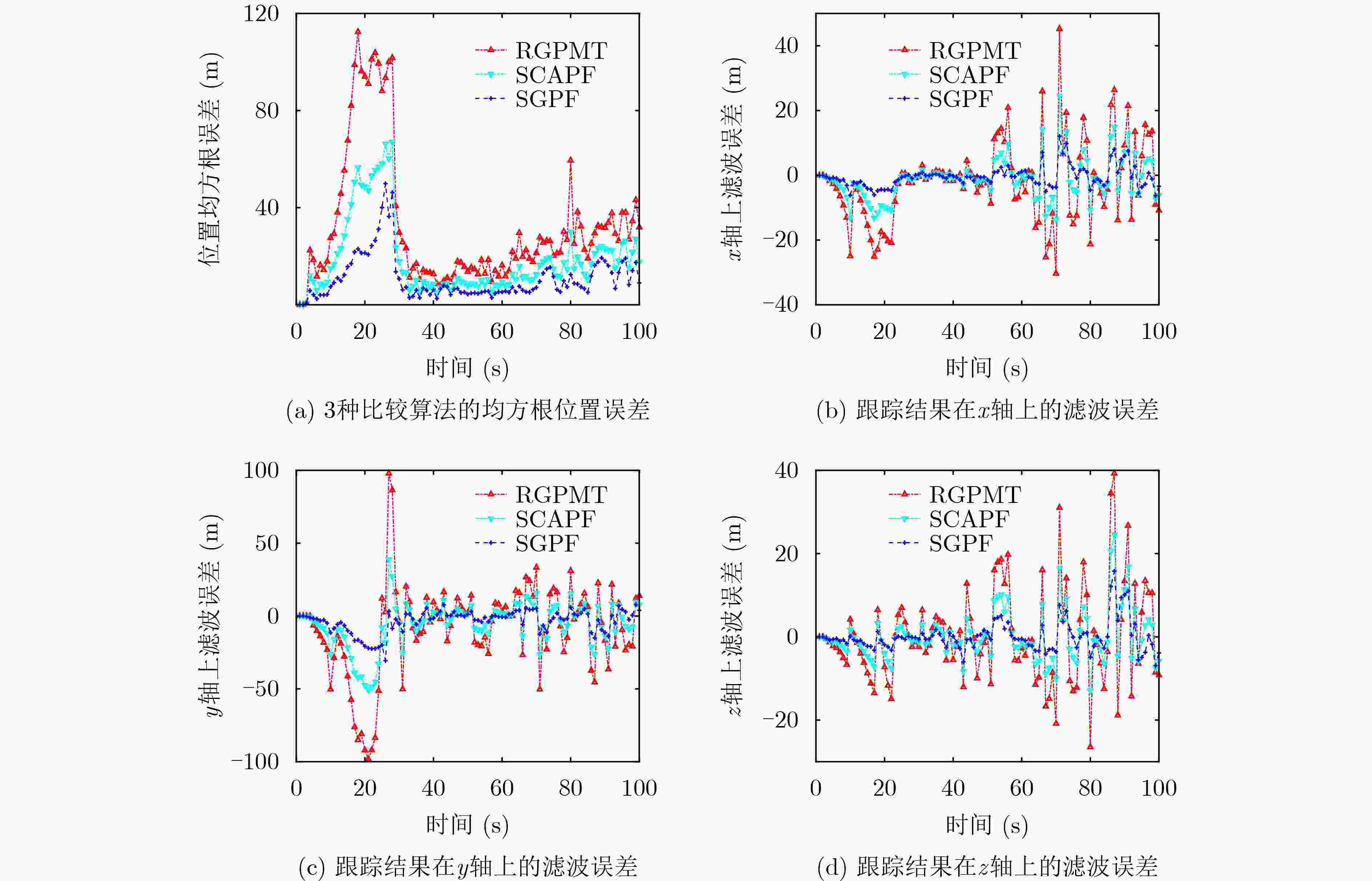
摘要: 为消减仅测角机动目标跟踪系统中由时空不一致引起的投影基点偏移和高斯截断两类误差,该文采用映射表示和$ {\ell _1} $-$ {\ell _{2,1}} $稀疏正则表征时空因果一致约束,引入模糊综合贴近度建立次优建议分布,构建因果不变结构传递粒子集合以近似目标后验高斯积分,推导原始对偶高斯粒子滤波(PDGPF)算法。实验结果表明,相比交会测量最小二乘法,PDGPF算法定位旋翼无人机(UAV)的精度提升了18.4%~69.6%。相比于软约束辅助粒子滤波(SCAPF)算法,PDGPF算法在时空映射一致约束下能够自适应地修正粒子的权值,从而更为准确、稳定地跟踪机动点目标,整体计算负担减小了12.9%。Abstract: To reduce the mapping basepoint offset and Gaussian truncation errors caused by spatiotemporal inconsistency in angle-only maneuvering target tracking systems, mapping representation and $ {\ell _1} $-$ {\ell _{2,1}} $ sparse regularization to represent spatiotemporal causal consistency constraints are used, the fuzzy comprehensive closeness is introduced to establish the suboptimal proposal distribution, the particle set in a causal invariant structure to approximate the Gaussian integration for target posterior is propagated, and the Primal-Dual Gaussian Particle Filtering (PDGPF) algorithm is derived. Simulation results show that, compared to the intersection measurement method with least squares, the accuracy for the PDGPF to locate a rotor Unmanned Aerial Vehicle (UAV) has improved by 18.4%~69.6%. Compared to the Soft Constrained Auxiliary Particle Filtering (SCAPF) algorithm, the PDGPF algorithm can adaptively correct the particle weights under the spatiotemporal mapping consistent constraints, obtaining more accurate and stable state estimation for tracking a maneuvering point target, reducing the overall computational burden by 12.9%.
-
Key words:
- Maneuvering target tracking /
- Angle-only /
- Spatiotemporal inconsistency /
- Primal-dual /
- Causal invariant
-
表 1 交会测量最小二乘法和PDGPF算法定位旋翼无人机在3轴上的投影误差
交会测量最小二乘法 PDGPF算法 最大值 (m) 方差 (m2) 最大值(m) 方差 (m2) $ x $轴 4.85 1.18 4.51 1.10 $ y $轴 11.86 4.12 6.04 1.60 $ z $轴 9.33 3.95 3.35 1.20 表 2 100轮蒙特卡罗实验统计滤波误差(均值、协方差)和1轮蒙特卡罗实验运行时间
算法 位置均方根误差 $ x $轴上滤波误差 $ y $轴上滤波误差 $ z $轴上滤波误差 运行时间 (s) 均值 (m) 协方差 (m2) 最大值 (m) 协方差 (m2) 最大值 (m) 协方差 (m2) 最大值 (m) 协方差 (m2) RGPMT 32.32 27.74 45.25 12.71 98.00 31.99 39.28 11.42 0.118 SCAPF 18.82 15.59 24.50 6.53 –50.53 15.76 24.58 6.16 1.442 PDGPF 10.72 9.14 12.06 3.33 –30.61 7.76 15.76 3.65 1.278 -
[1] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part I. Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333–1364. doi: 10.1109/TAES.2003.1261132. [2] BAR-SHALOM Y, LI X R, and KIRUBARAJAN T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software[M]. New York: John Wiley & Sons, 2002. [3] 何友, 王国宏, 陆大䋮, 等. 多传感器信息融合及应用[M]. 2版. 北京: 电子工业出版社, 2007: 7–10.HE You, WANG Guohong, LU Dajin, et al. Multisensor Information Fusion with Applications[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2007: 7–10. [4] 韩飞, 刘付成, 王兆龙, 等. 多空间机器人协同的多视线仅测角相对导航[J]. 航空学报, 2021, 42(1): 524174. doi: 10.7527/S1000-6893.2020.24174.HAN Fei, LIU Fucheng, WANG Zhaolong, et al. Multiple line-of-sight angles-only relative navigation by multiple collaborative space robots[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(1): 524174. doi: 10.7527/S1000-6893.2020.24174. [5] 王昱淇, 卢宙, 蔡云泽. 基于一致性的分布式变结构多模型方法[J]. 自动化学报, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091.WANG Yuqi, LU Zhou, and CAI Yunze. Consensus-based distributed variable structure multiple model[J]. Acta Automatica Sinica, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091. [6] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part V. Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255–1321. doi: 10.1109/TAES.2005.1561886. [7] 王常虹, 张大力, 夏红伟, 等. GEO混合推力机动目标跟踪IMM算法[J]. 宇航学报, 2023, 44(3): 443–453. doi: 10.3873/j.issn.1000-1328.2023.03.013.WANG Changhong, ZHANG Dali, and XIA Hongwei, et al. An IMM algorithm for tracking GEO maneuvering target with hybrid thrust[J]. Journal of Astronautics, 2023, 44(3): 443–453. doi: 10.3873/j.issn.1000-1328.2023.03.013. [8] ASFIA U, RADHAKRISHNAN R, and SHARMA S N. Three-dimensional bearings-only target tracking: Comparison of few sigma point Kalman filters[M]. GU J, DEY R, and ADHIKARY N. Communication and Control for Robotic Systems. Singapore: Springer, 2022: 273–289. [9] 杜荣华, 廖文和, 张翔. 基于自适应均方根EKF的惯性辅助航天器仅测角导航方法[J]. 中国惯性技术学报, 2022, 30(2): 210–217,223. doi: 10.13695/j.cnki.12-1222/o3.2022.02.011.DU Ronghua, LIAO Wenhe, ZHANG Xiang. Inertial-aided spacecraft angles-only navigation method based on adaptive square-root EKF[J]. Journal of Chinese Inertial Technology, 2022, 30(2): 210–217,223. doi: 10.13695/j.cnki.12-1222/o3.2022.02.011. [10] 龚柏春, 金鑫, 张仁勇, 等. 基于相对角动量的空间非合作目标机动仅测角检测方法[J]. 系统工程与电子技术, 2023, 45(3): 814–821. doi: 10.12305/J.issn.1001-506X.2023.03.23.GONG Baichun, JIN Xin, ZHANG Renyong, et al. Angle-only measurement maneuver detecting method for space non-cooperative target based on relative angular momentum[J]. Systems Engineering and Electronics, 2023, 45(3): 814–821. doi: 10.12305/J.issn.1001-506X.2023.03.23. [11] AFTAB W and MIHAYLOVA L. A Gaussian process regression approach for point target tracking[C]. 2019 22th International Conference on Information Fusion (FUSION), Ottawa, Canada, 2019: 1–8. [12] AFTAB W and MIHAYLOVA L. A learning Gaussian process approach for maneuvering target tracking and smoothing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 278–292. doi: 10.1109/TAES.2020.3021220. [13] 张小虎, 曹勇. 贝叶斯序贯重要性积分滤波器[J]. 电子学报, 2022, 50(4): 82–831. doi: 10.12263/DZXB.20210716.ZHANG Hong-wei, ZHANG Xiao-hu, CAO Yong. Bayesian Sequential Importance Quadrature Filter[J]. Acta Electonica Sinica, 2022, 50(4): 823–831. [14] VAN DER MERWE R, DOUCET A, DE FREITAS N, et al. The unscented particle filter[C]. The 13th International Conference on Neural Information Processing Systems, Denver, USA, 2000: 563–569. [15] DECHTER R. Constraint Processing[M]. Amsterdam: Elsevier, 2003: 34–35. [16] LI Baibing, LIU Cunjia, and CHEN Wenhua. An auxiliary particle filtering algorithm with inequality constraints[J]. IEEE Transactions on Automatic Control, 2017, 62(9): 4639–4646. doi: 10.1109/tac.2016.2624698. [17] LIU Cunjia, LI Baibing, and CHEN Wenhua. Particle filtering with soft state constraints for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3492–3504. doi: 10.1109/TAES.2019.2908292. [18] SIMON D. Kalman filtering with state constraints: a survey of linear and nonlinear algorithms[J]. IET Control Theory &Applications, 2010, 4(8): 1303–1318. doi: 10.1049/iet-cta.2009.0032. [19] ZHANG Hongwei, YE Xiaoyu, and HU Qi. Spatiotemporal learning via mixture importance Gaussian filtering with sparse regularization[J]. IEEE Signal Processing Letters, 2023, 30: 279–283. doi: 10.1109/LSP.2023.3258861. [20] 章涛, 张亚娟, 孙刚, 等. 稀疏贝叶斯字典学习空时机动目标参数估计算法[J]. 电子与信息学报, 2022, 44(8): 2884–2892. doi: 10.11999/JEIT210567.ZHANG Tao, ZHANG Yajuan, SUN Gang, et al. Maneuvering target parameter estimation based on sparse Bayesian dictionary learning in space-time adaptive processing[J]. Journal of Electronics &Information Technology, 2022, 44(8): 2884–2892. doi: 10.11999/JEIT210567. [21] GARCÍA-FERNÁNDEZ Á F, MORELANDE M R, and GRAJAL J. Mixture truncated unscented Kalman filtering[C]. 2012 15th International Conference on Information Fusion, Singapore, Singapore, 2012: 479–486. [22] LIM J, KIM H S, and PARK H M. Minimax particle filtering for tracking a highly maneuvering target[J]. International Journal of Robust and Nonlinear Control, 2020, 30(2): 636–651. doi: 10.1002/rnc.4785. [23] 胡小丽, 唐明刚, 蔡文泽, 等. 一种靶场关键段姿态交会测量优化布站分析方法[J]. 弹箭与制导学报, 2022, 42(5): 38–41. doi: 10.15892/j.cnki.djzdxb.2022.05.008.HU Xiaoli, TANG Minggang, CAI Wenze, et al. An optimal station layout analysis method for pose rendezvous measurement in key sections of shooting range[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2022, 42(5): 38–41. doi: 10.15892/j.cnki.djzdxb.2022.05.008. [24] LI X R. Compatibility and modeling of constrained dynamic systems[C]. 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 2016: 240–247. [25] DE GEETER J, VAN BRUSSEL H, DE SCHUTTER J, et al. A smoothly constrained Kalman filter[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(10): 1171–1177. doi: 10.1109/34.625129. [26] SÄRKKÄ S. Bayesian Filtering and Smoothing[M]. Cambridge: Cambridge University Press, 2013: 19. [27] CRASSIDIS J L and JUNKINS J L. Optimal Estimation of Dynamic Systems[M]. 2nd ed. New York: CRC Press, 2011: 261–262. [28] LI Kan and PRÍNCIPE J C. Functional Bayesian filter[J]. IEEE Transactions on Signal Processing, 2021, 70: 57–71. doi: 10.1109/TSP.2021.3132277. [29] 张宏伟. 双站纯方位空时软约束无迹粒子滤波算法[J]. 系统工程与电子技术, 2023, 45(5): 1261–1269. doi: 10.12305/j.issn.1001-506X.2023.05.01.ZHANG Hongwei. Dual-station unscented particle filter algorithm with spatiotemporal soft constraint[J]. Systems Engineering and Electronics, 2023, 45(5): 1261–1269. doi: 10.12305/j.issn.1001-506X.2023.05.01. [30] BECKERS S. Equivalent causal models[C]. The 35th AAAI Conference on Artificial Intelligence, Vancouver, Canada, 2021: 6202–6209. [31] 刘宗香, 谢维信, 黄敬雄, 等. 被动传感器网基于模糊综合贴近度的航迹起始[J]. 电子学报, 2007, 35(8): 1476–1480. doi: 10.3321/j.issn:0372-2112.2007.08.011.LIU Zongxiang, XIE Weixin, HUANG Jingxiong, et al. Fuzzy track initiation algorithm in the passive sensor network[J]. Acta Electronica Sinica, 2007, 35(8): 1476–1480. doi: 10.3321/j.issn:0372-2112.2007.08.011. [32] IZANLOO R, FAKOORIAN S A, YAZDI H S, et al. Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise[C]. 2016 Annual Conference on Information Science and Systems (CISS), Princeton, USA, 2016: 500–505. -





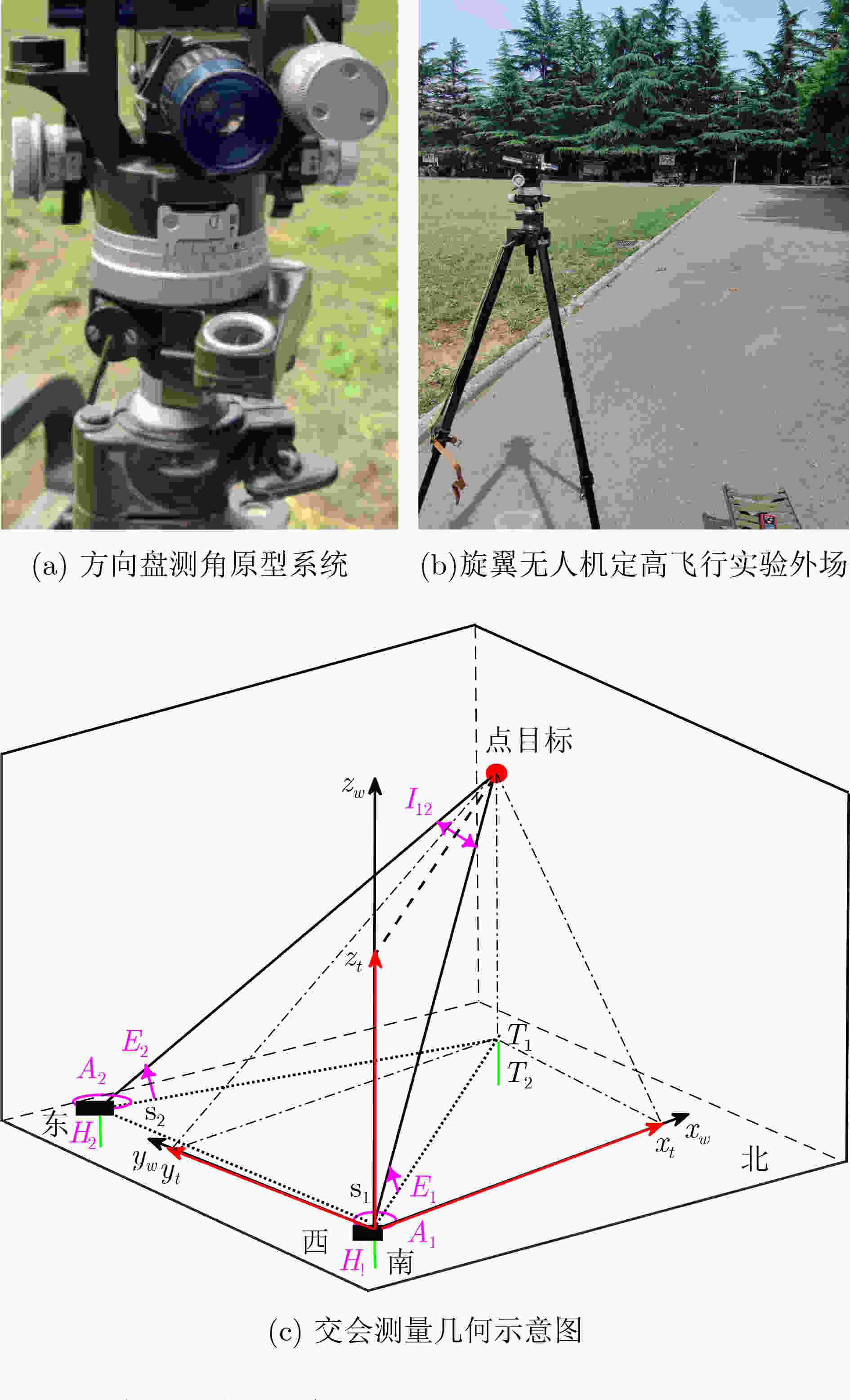
 下载:
下载:
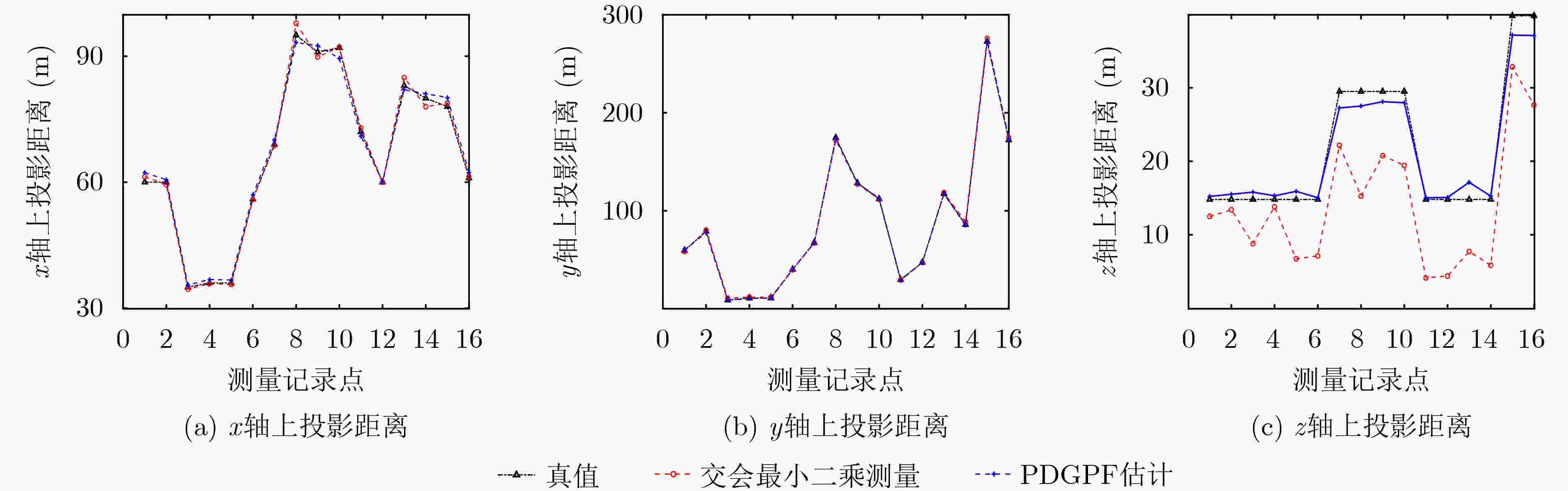
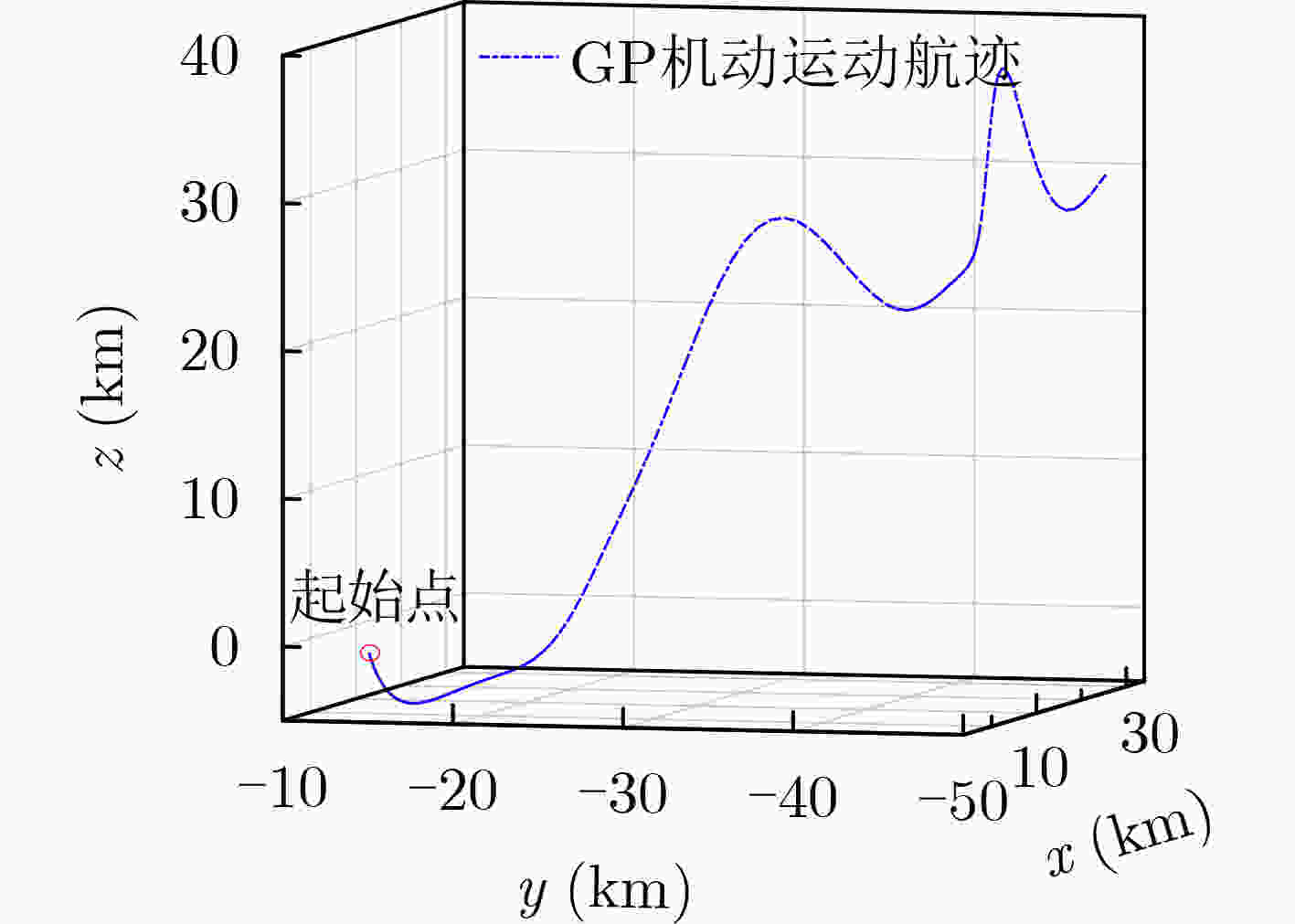
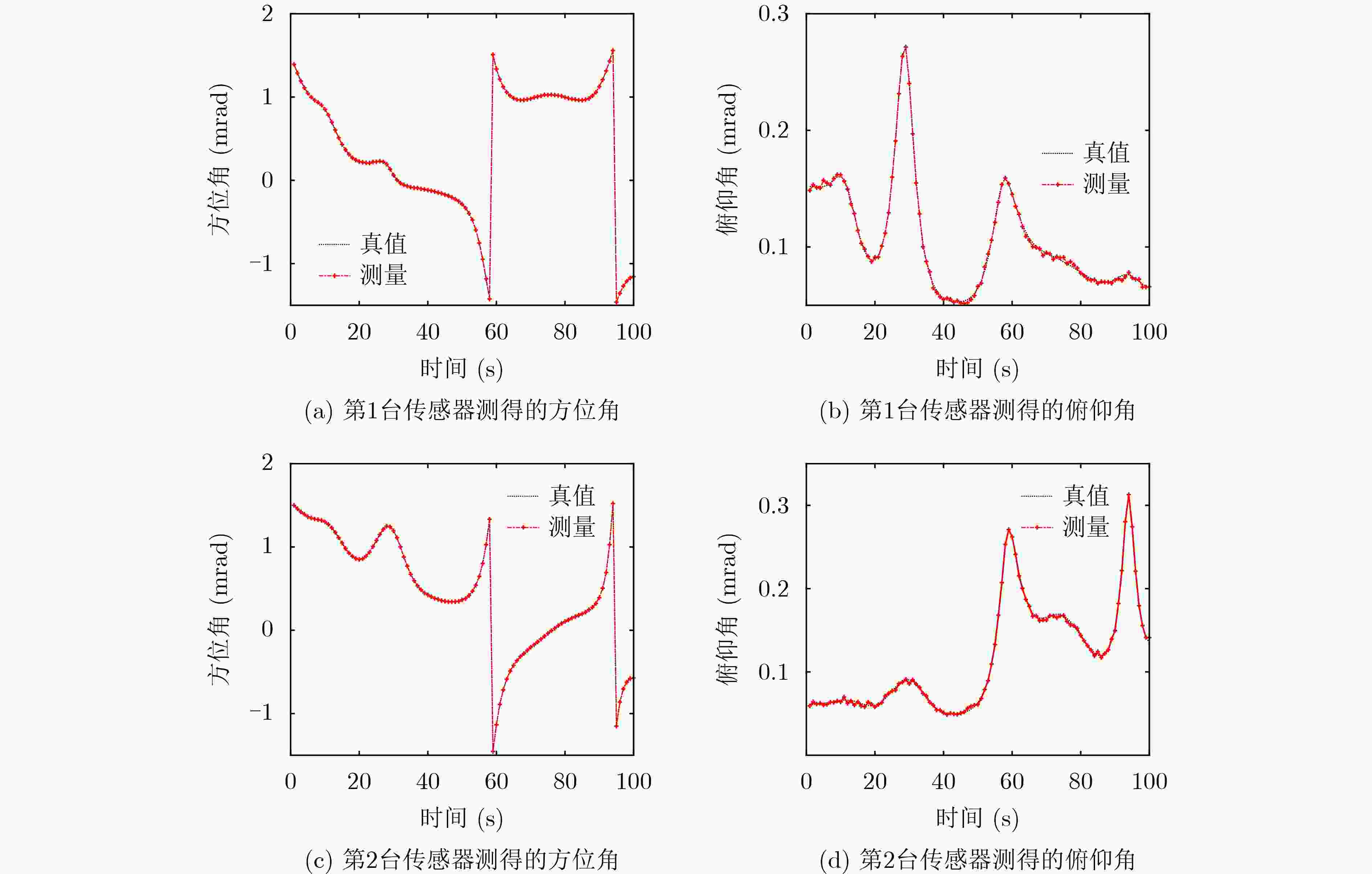


 下载:
下载:
