Efficient Parameters Estimation of Multi-target Based on Space-Time Cascaded Monopulse
-
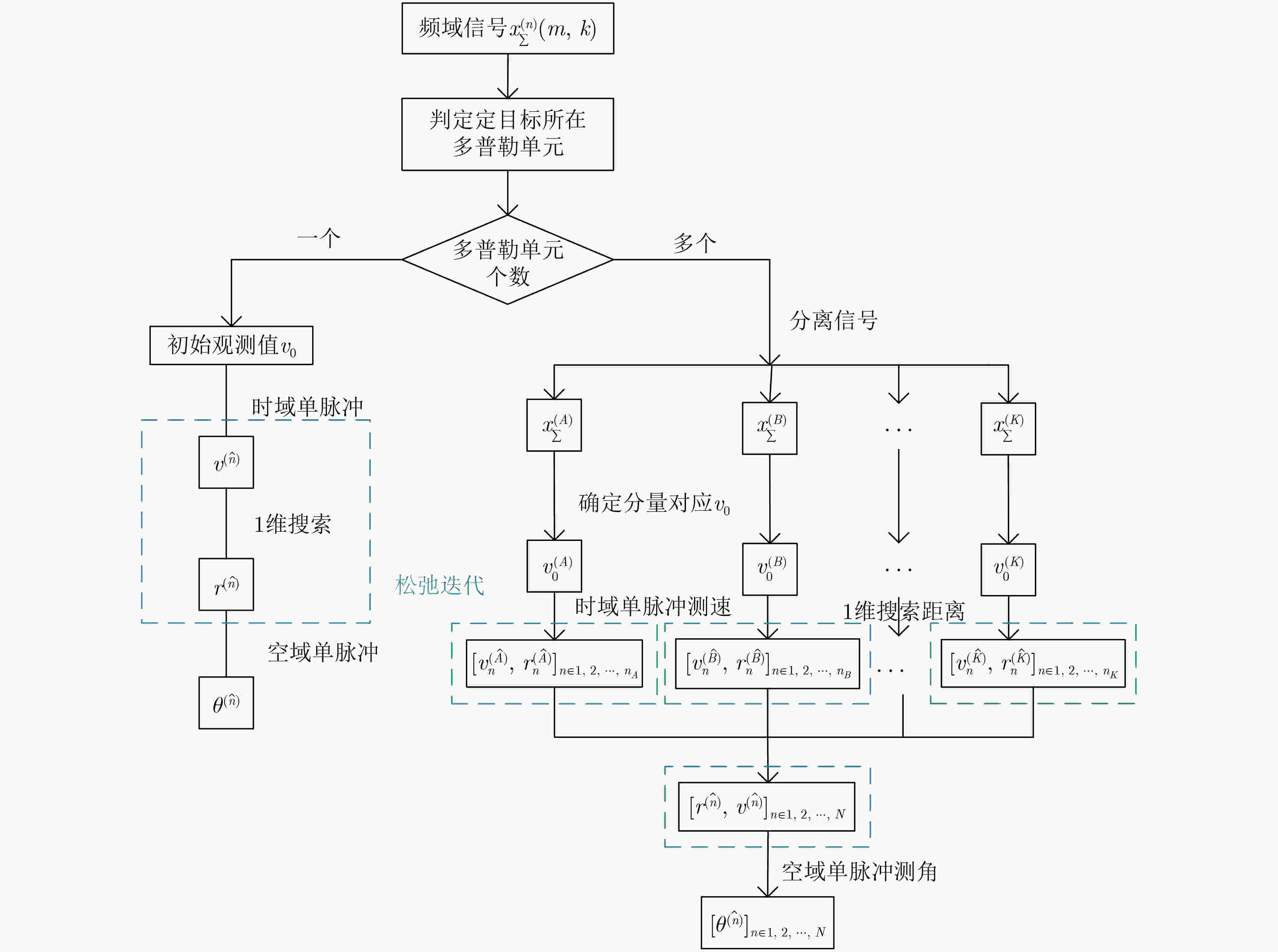
摘要: 比幅单脉冲最大似然算法(ACM-ML)在进行目标参数估计时需要进行距离与速度的2维松弛迭代搜索,导致了计算效率低、运算量大的问题。针对上述问题,该文提出一种基于空时级联单脉冲的高效多目标参数估计算法(M-STCMP算法)。该算法将单脉冲概念引入脉冲域,利用时域单脉冲计算目标速度,避免了ACM-ML算法中对速度的迭代搜索,将2维松弛迭代搜索降为1维搜索,有效降低了计算复杂度。考虑时域单脉冲无法同时匹配分布在不同时域主波束的速度各异的多个检测目标,进一步利用目标信号的多普勒信息,在各多普勒单元分别进行时域单脉冲测速,并搜索目标距离值。最后为抑制目标间的信号泄露,将所有目标的估计参数进行级联迭代获得高精度参数估计值。理论分析和仿真结果验证了M-STCMP算法的有效性。Abstract: An ACM-ML (Amplitude Comparison Monopulse-Maximum Likelihood) algorithm that employs a two-dimensional relaxation iterative search for range and velocity inevitably leads to low computational speeds and large amount calculation. Focusing on the problems mentioned above, a method for efficient Multi-target parameter estimation based on a Space-Time Cascaded MonoPulse algorithm (M-STCMP) is proposed in the paper. The algorithm introduces the monopulse technique to the pulse domain for target velocity computing with temporal monopulse, which results in a one-dimensional search for range and significantly reducing the computational burden of a two-dimensional iterative search within the ACM-ML algorithm. Because the temporal monopulse cannot simultaneously match multiple targets of varying velocities across main beams, the M-STCMP algorithm is improved by estimating the velocity in each Doppler cell with the Doppler information of received signals. To suppress energy leakage between targets, estimations produced in the main beams are cascaded and iterated for each target, that results in greater accuracy. Theoretical analysis and simulation verify the effectiveness of the proposed algorithm.
-
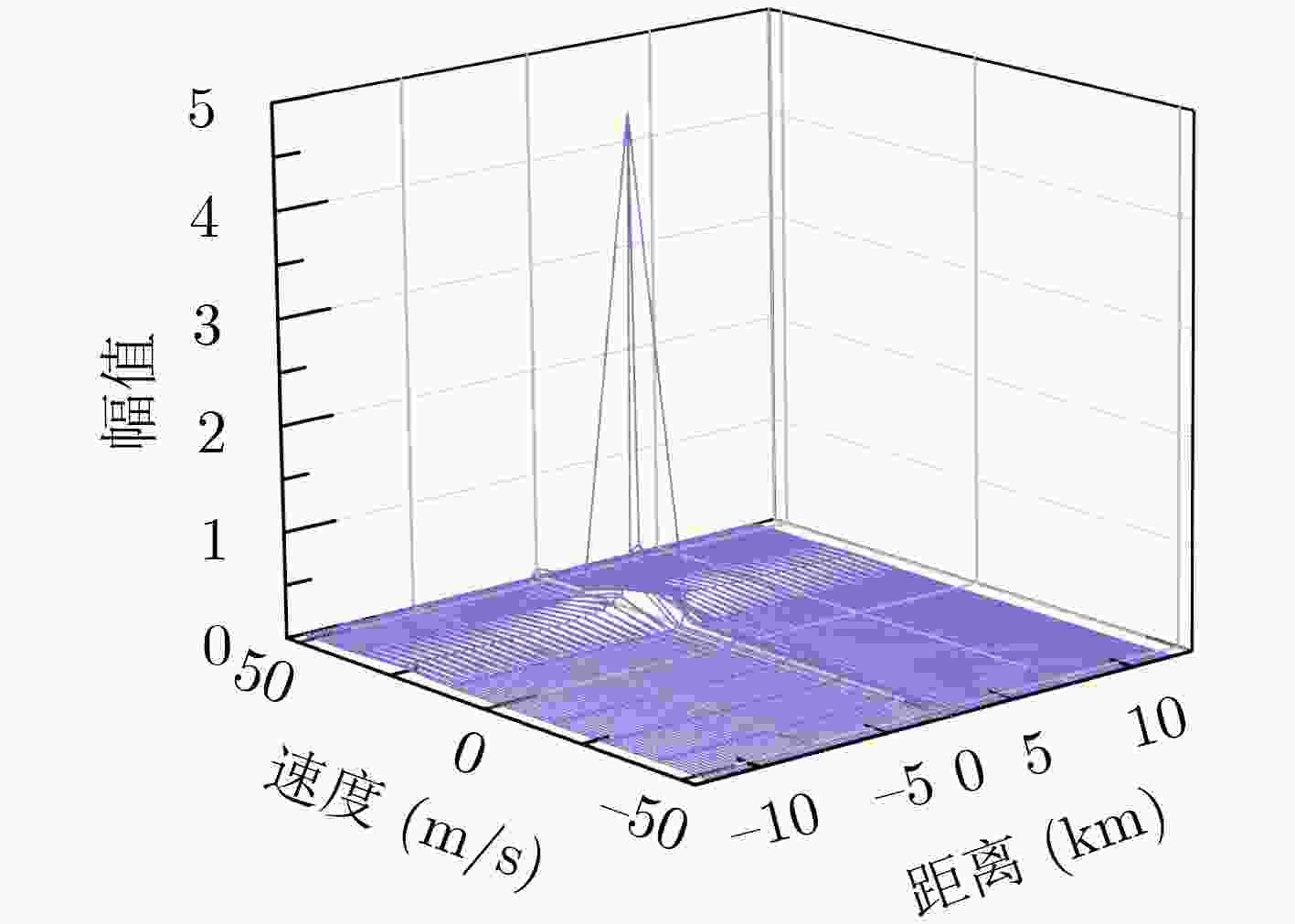
表 1 仿真1的目标参数信息
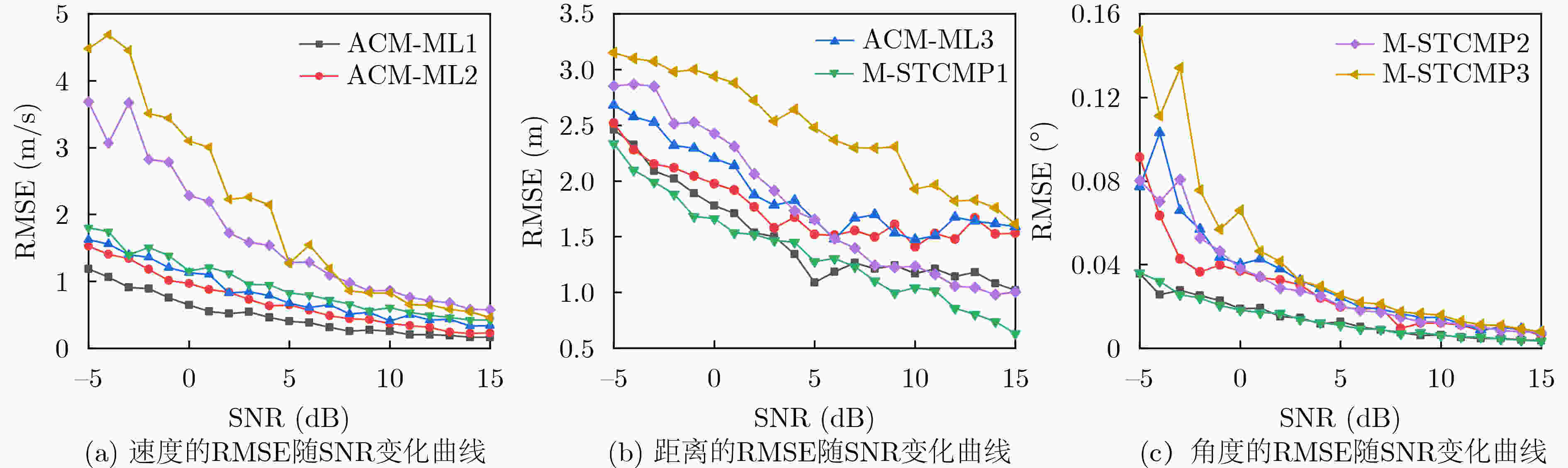
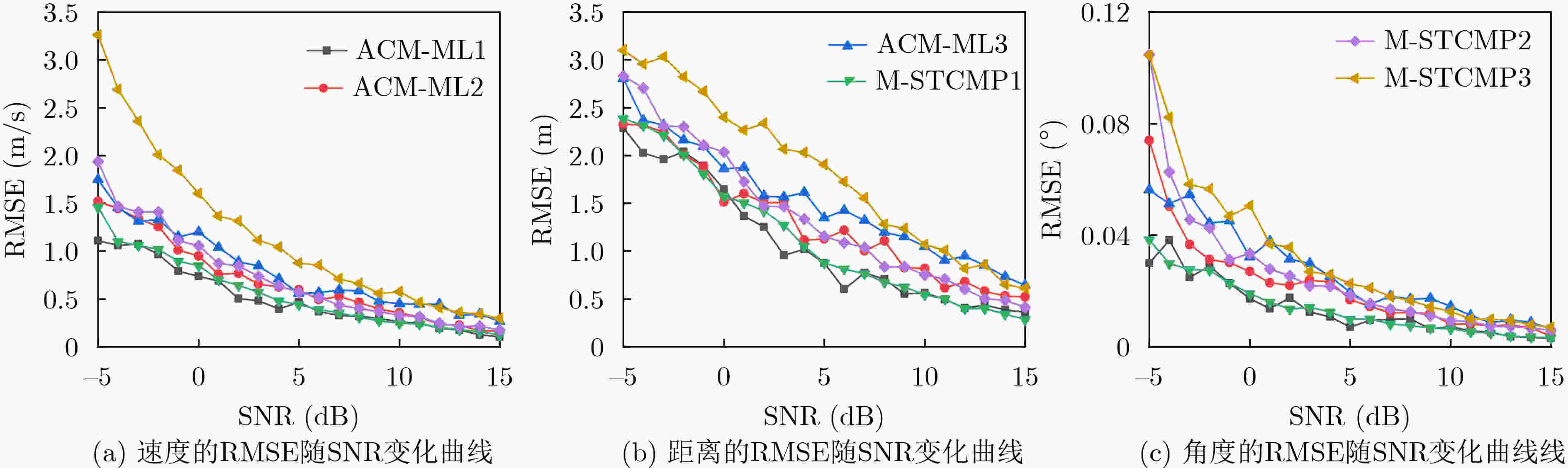
目标序号 1 2 3 速度(m/s) 27.9 25.6 23.7 多普勒单元 7 7 7 距离(m) 351.2 379.4 400.3 角度(°) 0.1 0.15 0.12 表 2 仿真2的目标参数信息
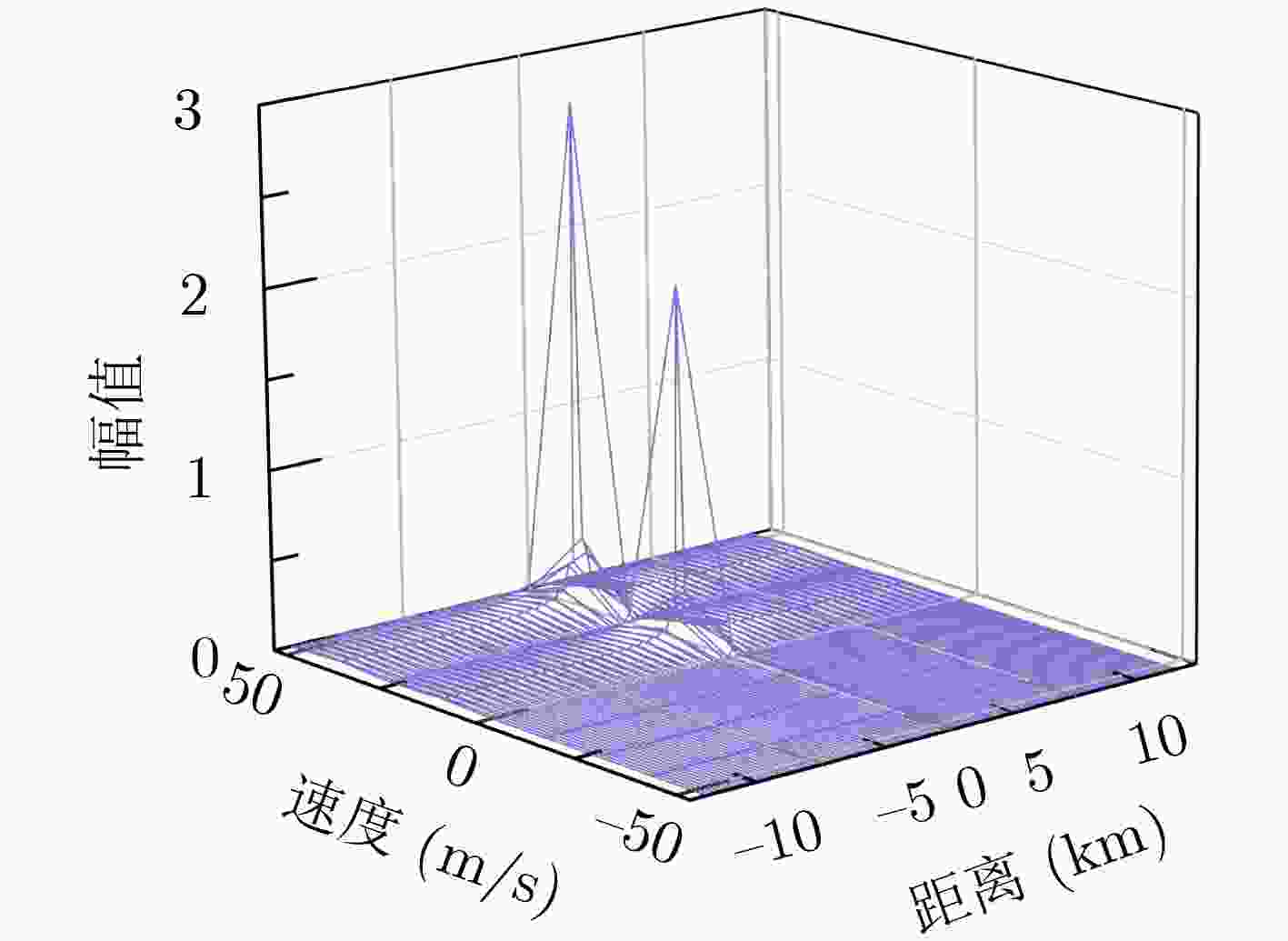
目标序号 1 2 3 速度(m/s) 11.9 41.3 13.8 多普勒单元 6 8 6 距离(m) 350.2 379.4 401.1 角度(°) 0.10 0.15 0.12 表 3 ACM-ML算法与M-STCMP算法单次运行时间对比
M-STCMP ACM-ML 运行时间(s) 315.0809 31392.9259 -
[1] BLAIR W D and BRANDT-PEARCE M. Unresolved Rayleigh target detection using monopulse measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(2): 543–552. doi: 10.1109/7.670335. [2] 吴迪, 杨成杰, 朱岱寅, 等. 一种用于单脉冲成像的自聚焦算法[J]. 电子学报, 2016, 44(8): 1962–1968. doi: 10.3969/j.issn.0372-2112.2016.08.027.WU Di, YANG Chengjie, ZHU Daiyin, et al. An autofocusing algorithm for monopulse imaging[J]. Acta Electronica Sinica, 2016, 44(8): 1962–1968. doi: 10.3969/j.issn.0372-2112.2016.08.027. [3] 周万幸. 空间导弹目标的捕获和处理[M]. 北京: 电子工业出版社, 2013: 15–18.ZHOU Wanxing. Acquisition and Processing of Space Missile Targets[M]. Beijing: Publishing House of Electronics Industry, 2013: 15–18. [4] HAN K and HONG S. MIMO Monopulse radar for detecting human targets with I/Q curve-length estimations[J]. IEEE Microwave and Wireless Components Letters, 2022, 32(3): 214–217. doi: 10.1109/LMWC.2022.3142322. [5] 王罗胜斌, 曾晖, 徐振海. 阵列雷达单脉冲群目标分辨方法[J]. 现代雷达, 2021, 43(9): 6–13. doi: 10.16592/j.cnki.1004-7859.2021.09.002.WANG Luoshengbin, ZENG Hui, and XU Zhenhai. Target resolution method of array radar via monopulse processing[J]. Modern Radar, 2021, 43(9): 6–13. doi: 10.16592/j.cnki.1004-7859.2021.09.002. [6] 黄倩兰, 蔡飞, 范红旗, 等. 密集假信号存在下单脉冲雷达未分辨目标DOA估计[J]. 系统工程与电子技术, 2023, 45(9): 2727–2734. doi: 10.12305/j.issn.1001-506x.2023.09.10.HUANG Qianlan, CAI Fei, FAN Hongqi, et al. DOA estimation of unresolved targets in the presense of dense false signals with monopulse radar[J]. Systems Engineering and Electronics, 2023, 45(9): 2727–2734. doi: 10.12305/j.issn.1001-506x.2023.09.10. [7] 李亚超, 王家东, 张廷豪, 等. 弹载雷达成像技术发展现状与趋势[J]. 雷达学报, 2022, 11(6): 943–973. doi: 10.12000/JR22119.LI Yachao, WANG Jiadong, ZHANG Tinghao, et al. Present situation and prospect of missile-borne radar imaging technology[J]. Journal of Radars, 2022, 11(6): 943–973. doi: 10.12000/JR22119. [8] 周克强. 针对无人机集群目标的舰炮对空射击方法[J]. 火力与指挥控制, 2021, 46(10): 84–88,95. doi: 10.3969/j.issn.1002-0640.2021.10.013.ZHOU Keqiang. Naval gun's anti-air firing method for UAV cluster target[J]. Fire Control & Command Control, 2021, 46(10): 84–88,95. doi: 10.3969/j.issn.1002-0640.2021.10.013. [9] SHERMAN S M. Complex indicated angles applied to unresolved radar targets and multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, AES-7(1): 160–170. doi: 10.1109/TAES.1971.310264. [10] LEE S P, CHO B L, LEE S M, et al. Unambiguous angle estimation of unresolved targets in monopulse radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1170–1177. doi: 10.1109/TAES.2014.140178. [11] BLAIR W D and BRANDT-PEARCE M. Unresolved Rayleigh target detection using monopulse measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(2): 543–552. doi: 10.1109/7.670335. [12] BLAIR W D and BRANDT-PEARCE M. Monopulse DOA estimation of two unresolved Rayleigh targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 452–469. doi: 10.1109/7.937461. [13] SINHA A, KIRUBARAJAN T and BAR-SHALOM Y. Maximum likelihood angle extractor for two closely spaced targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 183–201. doi: 10.1109/7.993239. [14] ZHENG Yibin, TSENG S M and YU K B. Closed-form four-channel monopulse two-target resolution[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 1083–1089. doi: 10.1109/TAES.2003.1238760. [15] GINI F, GRECO M, and FARINA A. Multiple radar targets estimation by exploiting induced amplitude modulation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1316–1332. doi: 10.1109/TAES.2003.1261131. [16] GRECO M, GINI F, and FARINA A. Joint use of sum and delta channels for multiple radar target DOA estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1146–1154. doi: 10.1109/TAES.2007.4383604. [17] FU Maozhong, GAO Chunxian, LI Yuhan, et al. Monopulse-radar angle estimation of multiple targets using multiple observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(2): 968–983. doi: 10.1109/TAES.2020.3035434. [18] XU Jia, YU Ji, PENG Yingning, et al. Radon-fourier transform for radar target detection, I: generalized doppler filter bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1186–1202. doi: 10.1109/TAES.2011.5751251. [19] TAO Ding, ANFINSEN S N, and BREKKE C. Robust CFAR detector based on truncated statistics in multiple-target situations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 117–134. doi: 10.1109/TGRS.2015.2451311. [20] BRADLEY E L. The equivalence of maximum likelihood and weighted least squares estimates in the exponential family[J]. Journal of the American Statistical Association, 1973, 68(341): 199–200. doi: 10.1080/01621459.1973.10481364. [21] 王旭东, 张迪, 闫贺. 基于Relax算法的星载高分宽幅成像方法研究[J]. 电子与信息学报, 2019, 41(5): 1077–1083. doi: 10.11999/JEIT180596.WANG Xudong, ZHANG Di, and YAN He. Research on spaceborne high resolution wide swath imaging method based on relax algorithm[J]. Journal of Electronics & Information Technology, 2019, 41(5): 1077–1083. doi: 10.11999/JEIT180596. [22] WARD J. Maximum likelihood angle and velocity estimation with space-time adaptive processing radar[C]. Conference Record of the Thirtieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1996: 1265–1267. doi: 10.1109/ACSSC.1996.599148. [23] ZOU Zegang, HAO Ming, and HE Qiang. An unambiguous angle estimation method based on multiple subarray division in DCAR[C]. 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 2021: 1561–1565. doi: 10.1109/ITNEC52019.2021.9587203. -





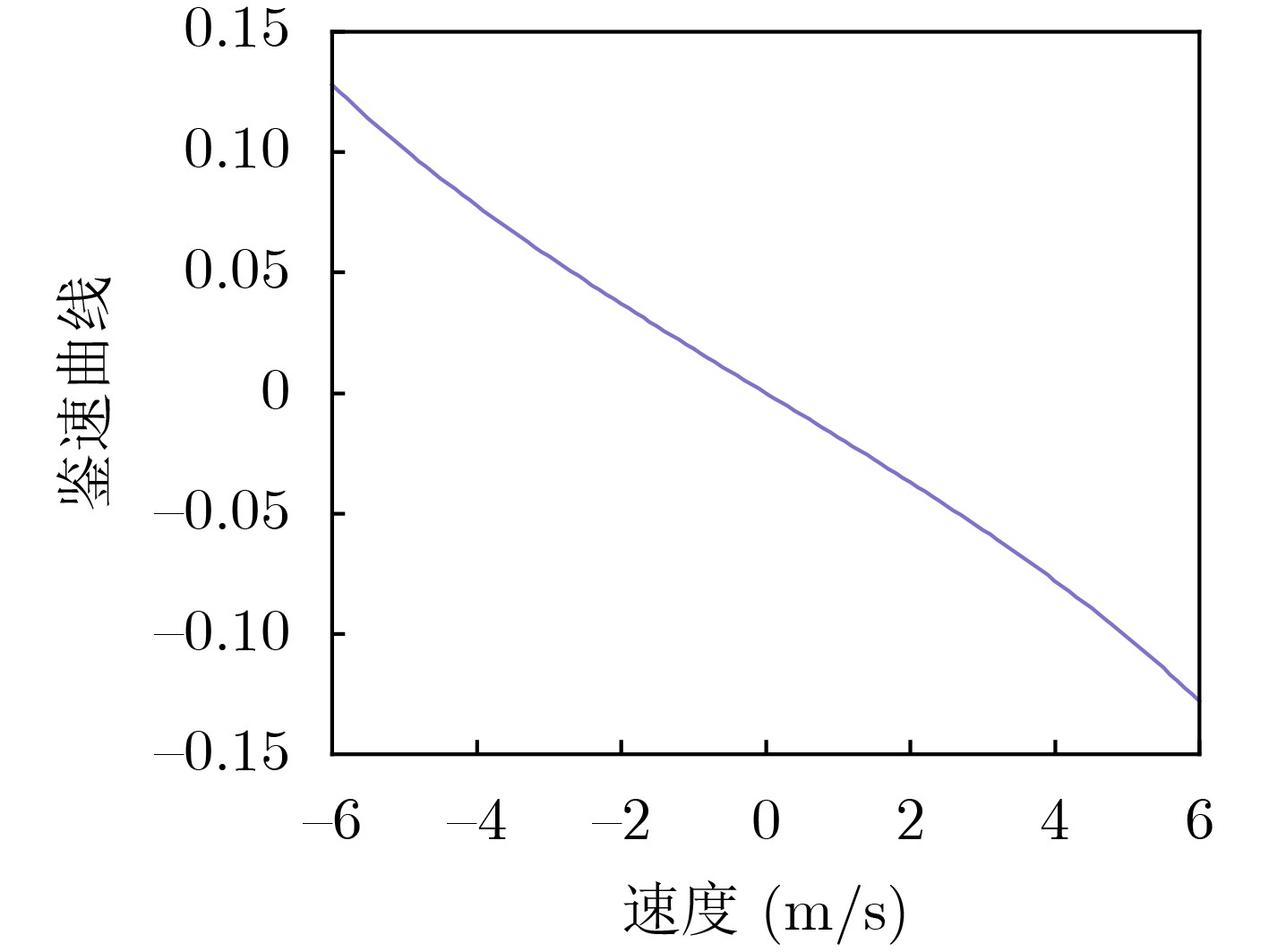
 下载:
下载:


 下载:
下载:
