High Accuracy Carrier Frequency Estimation of Multi-band Communication Signals Based on Undersampling
-
摘要: 为根本解决当前主流的基于调制宽带转化器(MWC )的欠采样频率估计方法存在的3个问题,即采样通道数目多、载频估计精度低、信源频带分布稀疏度条件高,该文提出基于互素谱相位差校正的通信信号载频估计方法。通过将两路互素欠采样取代多路调制宽带转化器欠采样,克服了其耗费欠采样通道数目多的缺陷;基于此,既推导出全景谱谱峰位置与两路互素输出IDFT支路序号对的映射关系,又推导出相邻快拍下该序号对的IDFT相位差与载频值的解析关系,从而克服了主流方法的载频估计精度低的缺陷;通过将最小尺寸全相位滤波器对半分解方法融入原型滤波器设计,构造出两路并行互素谱分析器,还彻底克服了对信源频带分布稀疏度条件高的依赖。仿真表明,相比于主流方法,该文方法仅需耗费不足其1/2的样本数量,载频估计的相对误差降至其1/20以下。Abstract: To essentially overcome the 3 deficiencies of the mainstream Modulation Wideband Converter (MWC )-based undersampling frequency estimator (i.e., over-consumption of undersampling channels, low accuracy of carrier frequency estimation, high sparsity of the source distribution), this paper proposes the phase-difference corrector based on coprime spectral analysis for the carrier frequency estimation of multi-band communication signals. Specifically, by substituting the multi-path MWC undersampling with the 2-path coprime undersampling, the consumption of undersampling channels is greatly reduced; Further, by developing the mapping relationship between the panoramic spectrum peak indices and the IDFT index pairs of coprime analyzers, the phase difference of the adjacent snapshots’ IDFT outputs corresponding to these index pairs can be analytically extracted, thus achieving much higher estimation accuracy compared to the mainstream MWC method. Meanwhile, by means of incorporating the minimum-sized half-decomposition based all-phase filter design into the prototype filter design, a two-path paralleled coprime spectral analyzer can be constructed, which thoroughly gets rid of the dependency of the high sparsity of the source distribution. Numerical results show that, compared to the mainstream MWC method, the proposed spectral corrector’s estimation error is no more than 1/20 of the former, while only consuming less than half of the sample amount.
-
1 多频带通信信号载频估计流程
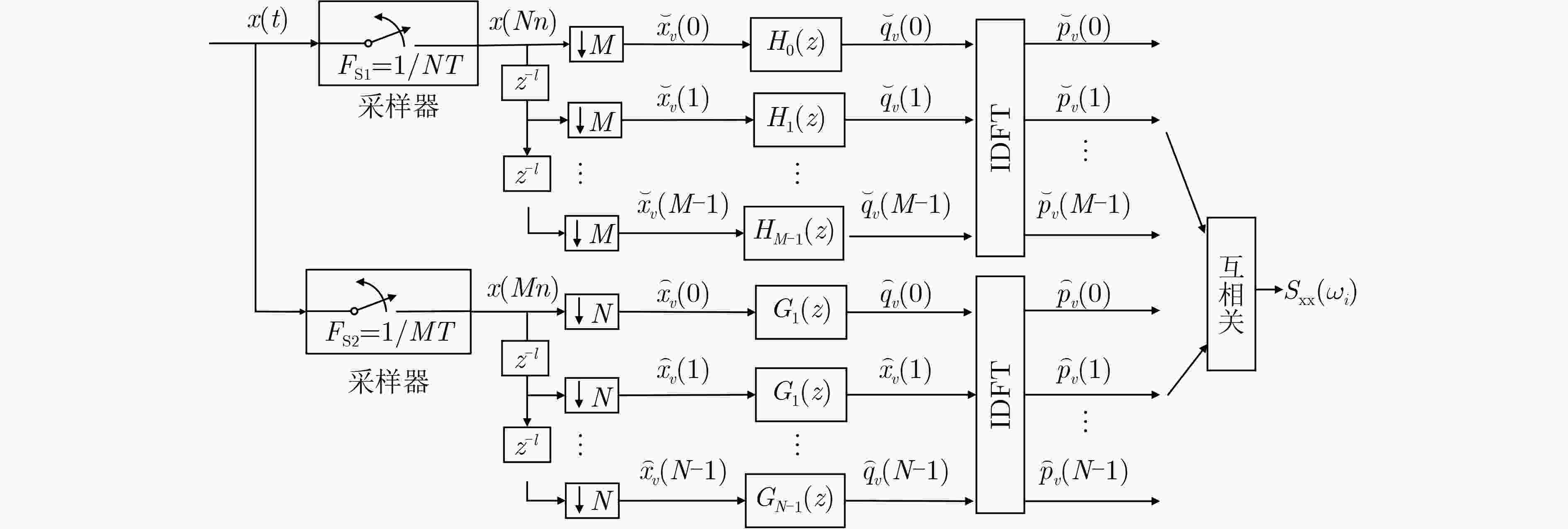
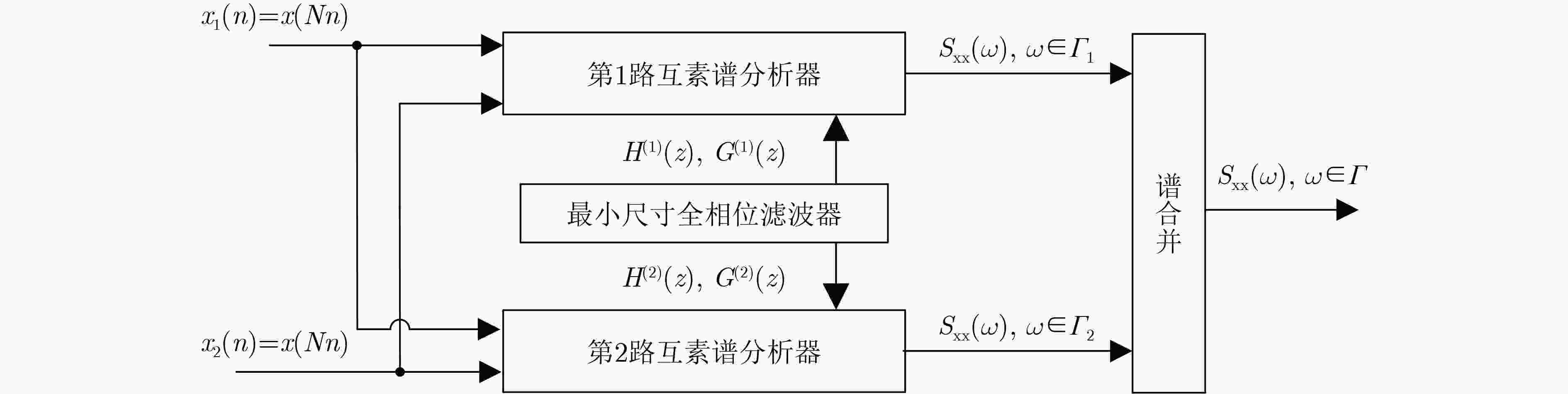
初始化 给定谱分析检测上限$ {F_N} $,设定互素整数对$ M,\;N $,依据式(17)设计两路并行互素谱分析器的原型滤波器;确定欠采样速率$ {F_{{{\mathrm{S}}}1}} = {{{F_{N}}} \mathord{\left/ {\vphantom {{{F_{N}}} N}} \right. } N} $, $ {F_{\rm{S}2}} = {{{F_{N}}} \mathord{\left/ {\vphantom {{{F_{N}}} M}} \right. } M} $,给定持续L+1个快拍时段的互素欠采样样本$ {x_1}(n) = x(Nn) $, $ {x_2}(n) = x(Mn) $; 步骤1 将$ {x_1}(n) $, $ {x_2}(n) $馈入两路并行互素谱分析器,获得全景谱,扫描其$[0,{F_{N}}/2)$范围内的所有谱峰; 步骤2 对于每个谱峰,依据式(18)的频点集合$ {\varGamma _1} $和$ {\varGamma _2} $,确定其所隶属的互素谱分析器以及所对应的谱序号i,将i代入式可得余数对k, l; 步骤3 在该互素谱分析器内,依据式(22)–式(24)分别计算上、下通道中第k路、第l路IDFT输出的L个相邻快拍相位差$ {\widehat{\delta }}_{v,k},{\widehat{\delta }}_{v,l},v=1,2,\cdots,L $,将其代入式(25)算出高精度的频偏估计值$ \hat \delta $; 步骤4 将谱序号i, $ \hat \delta $代入式可得该谱峰的估计值$ {\hat f_i} $; 步骤5 重复步骤 2~4,直至全景谱$[0,{F_{N}}/2)$范围内的全部谱峰估计完毕。 -
[1] ALI A and HAMOUDA W. Advances on spectrum sensing for cognitive radio networks: Theory and applications[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1277–1304. doi: 10.1109/COMST.2016.2631080. [2] ARJOUNE Y and KAABOUCH N. A comprehensive survey on spectrum sensing in cognitive radio networks: Recent advances, new challenges, and future research directions[J]. Sensors, 2019, 19(1): 126. doi: 10.3390/s19010126. [3] ZHANG Ling, WEI Zhiqing, WANG Lin, et al. Spectrum sharing in the sky and space: A survey[J]. Sensors, 2023, 23(1): 342. doi: 10.3390/s23010342. [4] LI Xiaowei, LIANG Hong, and XIA Xianggen. A robust Chinese remainder theorem with its applications in frequency estimation from undersampled waveforms[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4314–4322. doi: 10.1109/TSP.2009.2025079. [5] WANG Wenjie and XIA Xianggen. A closed-form robust Chinese remainder theorem and its performance analysis[J]. IEEE Transactions on Signal Processing, 2010, 58(11): 5655–5666. doi: 10.1109/TSP.2010.2066974. [6] LIU Shang, WANG Lulu, LIN Weibin, et al. Digital instantaneous frequency measurement with wide bandwidth for real-valued waveforms using multiple sub-Nyquist channels[J]. Measurement Science and Technology, 2023, 34(2): 025101. doi: 10.1088/1361-6501/ac97b. [7] SU Yu and JIANG Defu. Digital instantaneous frequency measurement of a real sinusoid based on three sub-Nyquist sampling channels[J]. Mathematical Problems in Engineering, 2020, 2020: 5089761. doi: 10.1155/2020/5089761. [8] MISHALI M and ELDAR Y C. From theory to practice: Sub-Nyquist sampling of sparse wideband analog signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 375–391. doi: 10.1109/JSTSP.2010.2042414. [9] 郑仕链, 杨小牛. 用于调制宽带转换器压缩频谱感知的重构失败判定方法[J]. 电子与信息学报, 2015, 37(1): 236–240. doi: 10.11999/JEIT140127.ZHENG Shilian and YANG Xiaoniu. A reconstruction failure detection scheme for modulated wideband converter based compressed spectrum sensing[J]. Journal of Electronics & Information Technology, 2015, 37(1): 236–240. doi: 10.11999/JEIT140127. [10] HE Jiai, CHEN Wei, JIA Lu, et al. An effective reconstruction algorithm based on modulated wideband converter for wideband spectrum sensing[J]. IEEE Access, 2020, 8: 152239–152247. doi: 10.1109/ACCESS.2020.3017729. [11] JIANG Siyi, FU Ning, WEI Zhiliang, et al. Joint spectrum, carrier, and DOA estimation with beamforming MWC sampling system[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 8001415. doi: 10.1109/TIM.2022.3147893. [12] SOBHANI G, PEZESHK A M, BEHNIA F, et al. Joint detection of carrier frequency and direction of arrival of wide-band signals using sub-Nyquist sampling and interferometric direction finding[J]. AEU-International Journal of Electronics and Communications, 2021, 139: 153926. doi: 10.1016/j.aeue.2021.153926. [13] 张展, 魏平, 高林, 等. 以欠采样速率实现盲谱感知及二维DOA估计[J]. 电子科技大学学报, 2022, 51(3): 357–362.ZHANG Zhan, WEI Ping, GAO Lin, et al. Achieving blind spectrum sensing and two-dimensional DOA estimation with sub-Nyquist sampling rate[J]. Journal of University of Electronic Science and Technology of China, 2022, 51(3): 357–362. [14] VAIDYANATHAN P P and PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682. [15] HUANG Xiangdong, HAN Yiwen, YAN Ziyang, et al. Resolution doubled Co-prime spectral analyzers for removing spurious peaks[J]. IEEE Transactions on Signal Processing, 2016, 64(10): 2489–2498. doi: 10.1109/TSP.2016.2526964. [16] 黄翔东, 单宇轩, 王健. 基于并行全相位点通滤波的高性能互素谱分析方法[J]. 电子与信息学报, 2020, 42(3): 613–620. doi: 10.11999/JEIT190317.HUANG Xiangdong, SHAN Yuxuan, and WANG Jian. High-performance co-prime spectral analysis method based on parallelled all-phase point-pass filtering[J]. Journal of Electronics & Information Technology , 2020, 42(3): 613–620. doi: 10.11999/JEIT190317. [17] 黄翔东, 韩溢文, 闫子阳, 等. 基于全相位滤波的互素谱分析的高效设计[J]. 系统工程与电子技术, 2017, 39(1): 27–33. doi: 10.3969/j.issn.1001-506X.2017.01.05.HUANG Xiangdong, HAN Yiwen, YAN Ziyang, et al. Efficient design of co-prime spectral analysis based on all-phase filtering[J]. Systems Engineering and Electronics, 2017, 39(1): 27–33. doi: 10.3969/j.issn.1001-506X.2017.01.05. -





 下载:
下载:


 下载:
下载:
