Orthogonal Time Sequency Multiplexing Waveform Framework Based on Multi-dimensional Extension and Its Performance Analysis
-
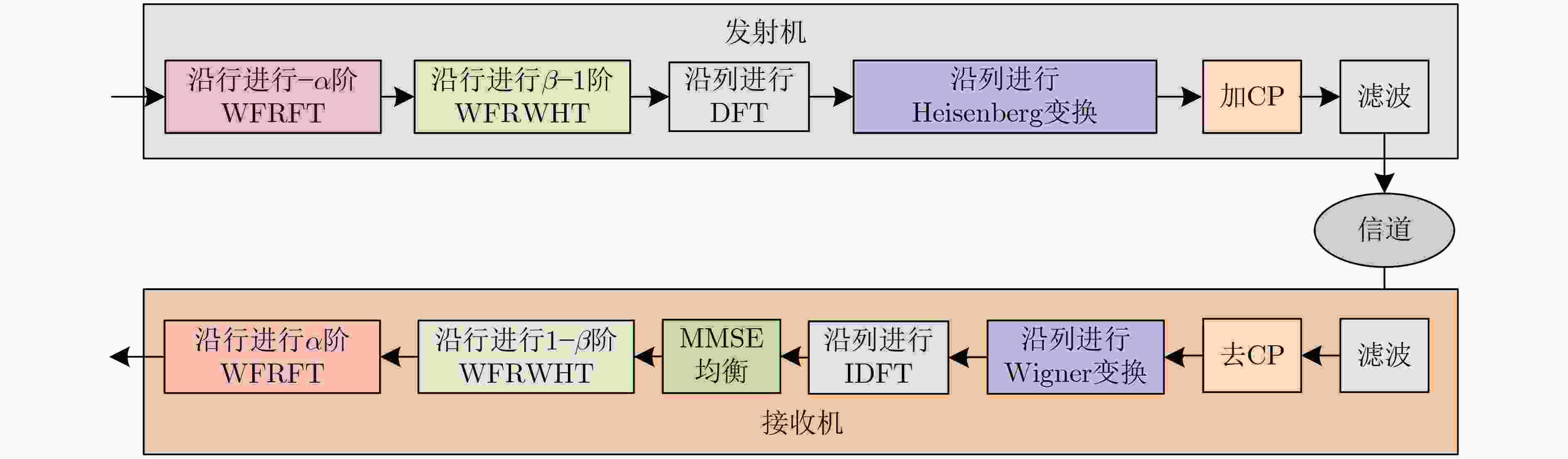
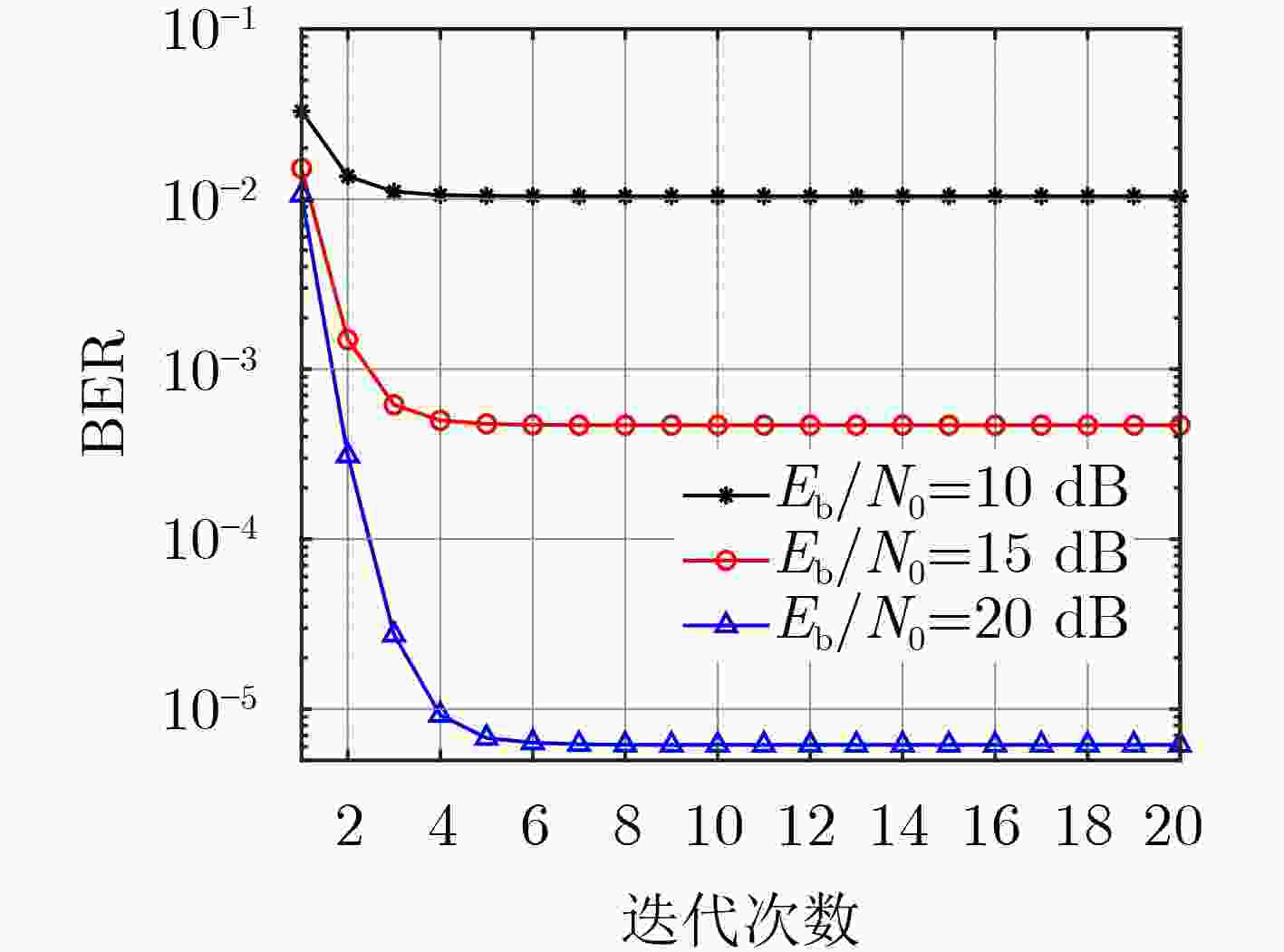
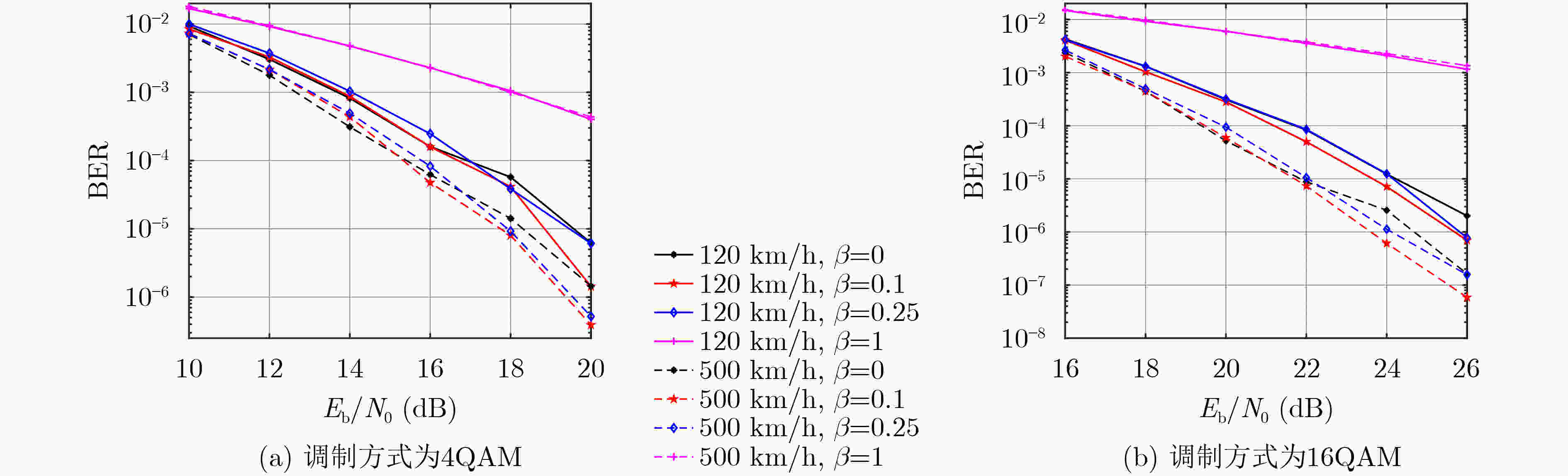
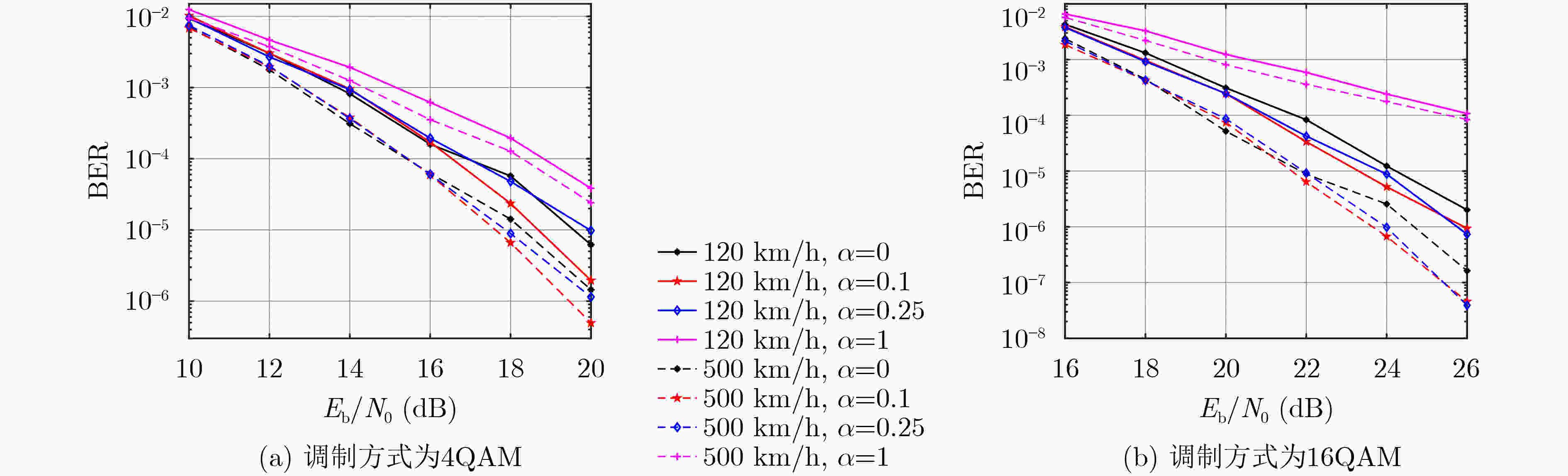
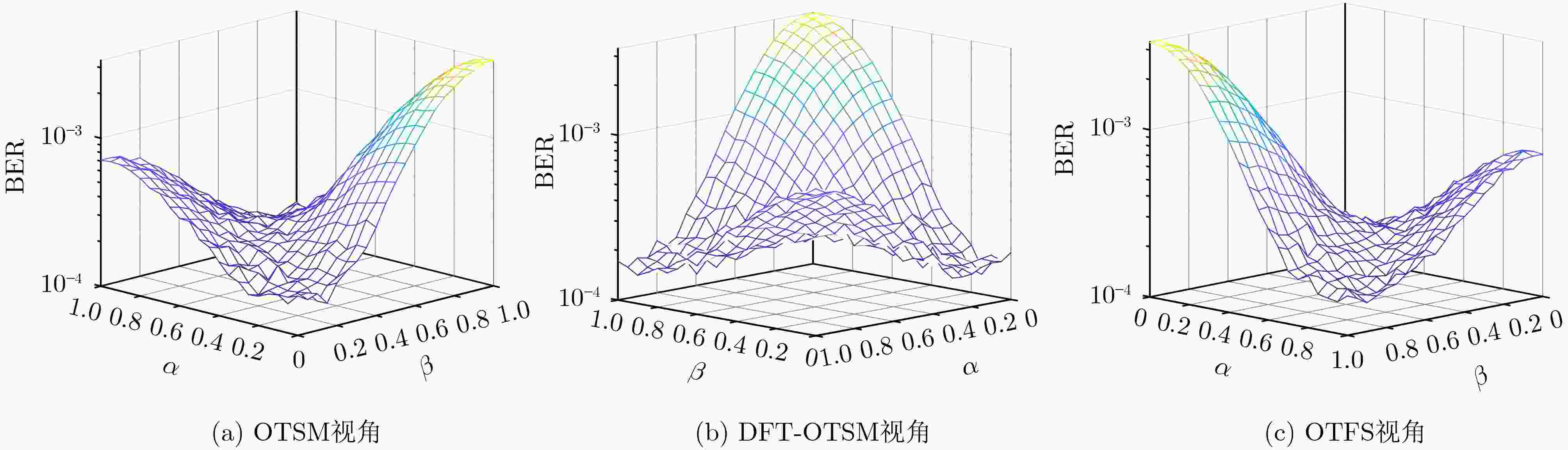
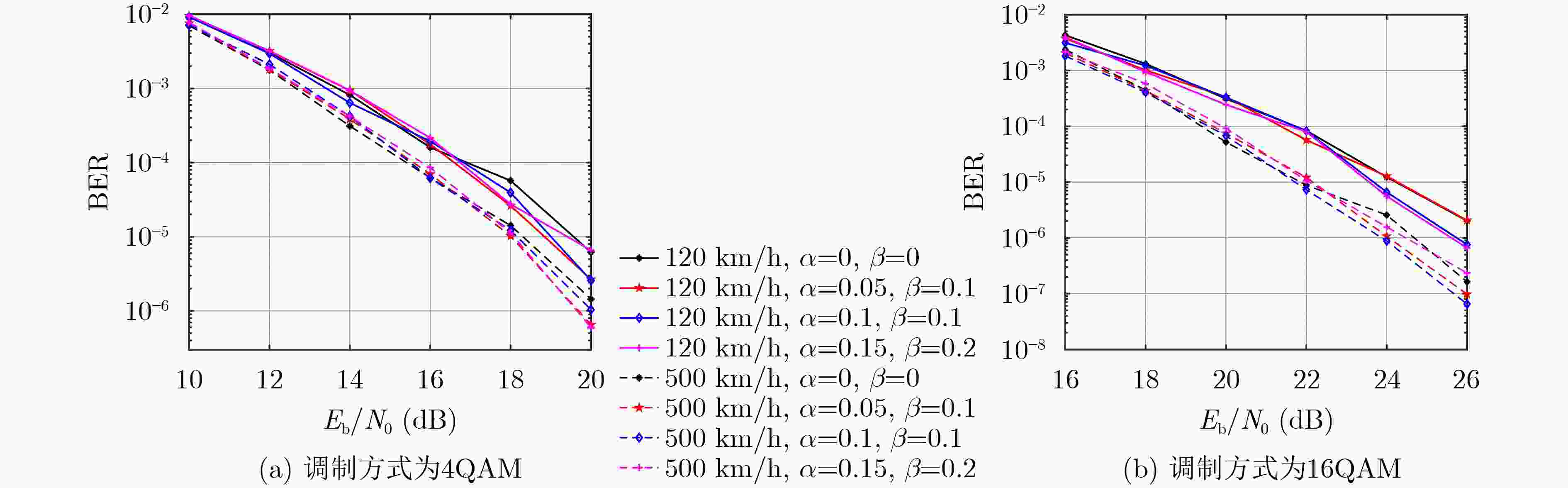
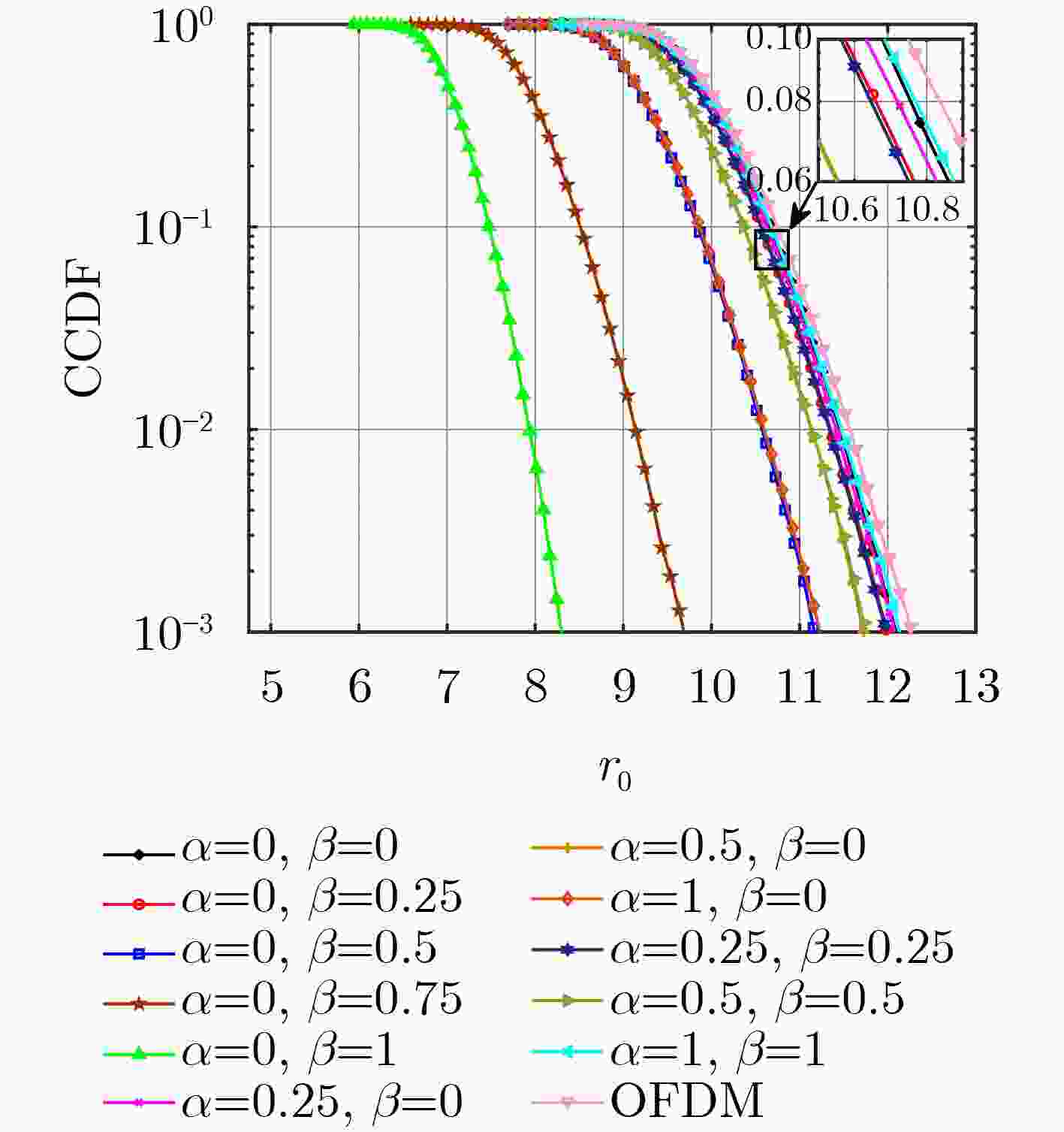
摘要: 正交时序复用(OTSM)是一种适用于高速移动场景的低复杂度调制方法。然而,单一的波形设计方法难以满足多样化的应用需求和性能需求。因此,该文基于加权分数傅里叶变换(WFRFT)提出了加权分数沃尔什-哈达玛变换(WFRWHT),并提出了多维扩展的一体化的加权分数傅里叶变换-加权分数沃尔什哈达玛变换-正交时序复用(WFRFT-WFRWHT-OTSM)波形框架。通过对2维参数的灵活配置,该框架可退化为OTSM、正交时频空、混合载波、正交频分复用和单载波等波形,同时研究了采用高斯-赛德尔(GS)迭代均衡时一体化WFRFT-WFRWHT-OTSM波形在时延-多普勒信道下的误码率(BER)性能以及峰均功率比(PAPR)性能。仿真结果表明,在不同时延-多普勒信道下,该框架可通过改变WFRFT和WFRWHT阶次实现更优的BER和PAPR性能。
-
关键词:
- 加权分数沃尔什变换 /
- 加权分数傅里叶变换 /
- 正交时序复用 /
- 正交频分复用 /
- 高斯-赛德尔迭代均衡
Abstract: Orthogonal Time Sequency Multiplexing (OTSM) is a low-complexity modulation method suitable for high-speed mobile scenarios. However, a single waveform design method is difficult to meet diverse application requirements and performance demands. Therefore, on basis of Weighted FRactional Fourier Transform (WFRFT), a Weighted FRactional Walsh-Hadamard Transform (WFRWHT) is proposed and an integrated WFRFT-WFRWHT-OTSM waveform framework based on multidimensional extensions is put forward. Through the flexible configuration of two-dimensional parameters, this framework can be degraded to different waveforms such as OTSM, orthogonal time-frequency-space, hybrid carrier, orthogonal frequency division multiplexing and single carrier. In addition, Bit Error Rate (BER) and Peak-to-Average Power Ratio (PAPR) performances of the integrated WFRFT-WFRWHT-OTSM framework over delay-Doppler channels are studied with Gauss-Seidel (GS) iteration equalization. Simulation results show that the proposed framework achieves better BER and PAPR performances through changing the order of WFRFT and WFRWHT over different delay-Doppler channels. -
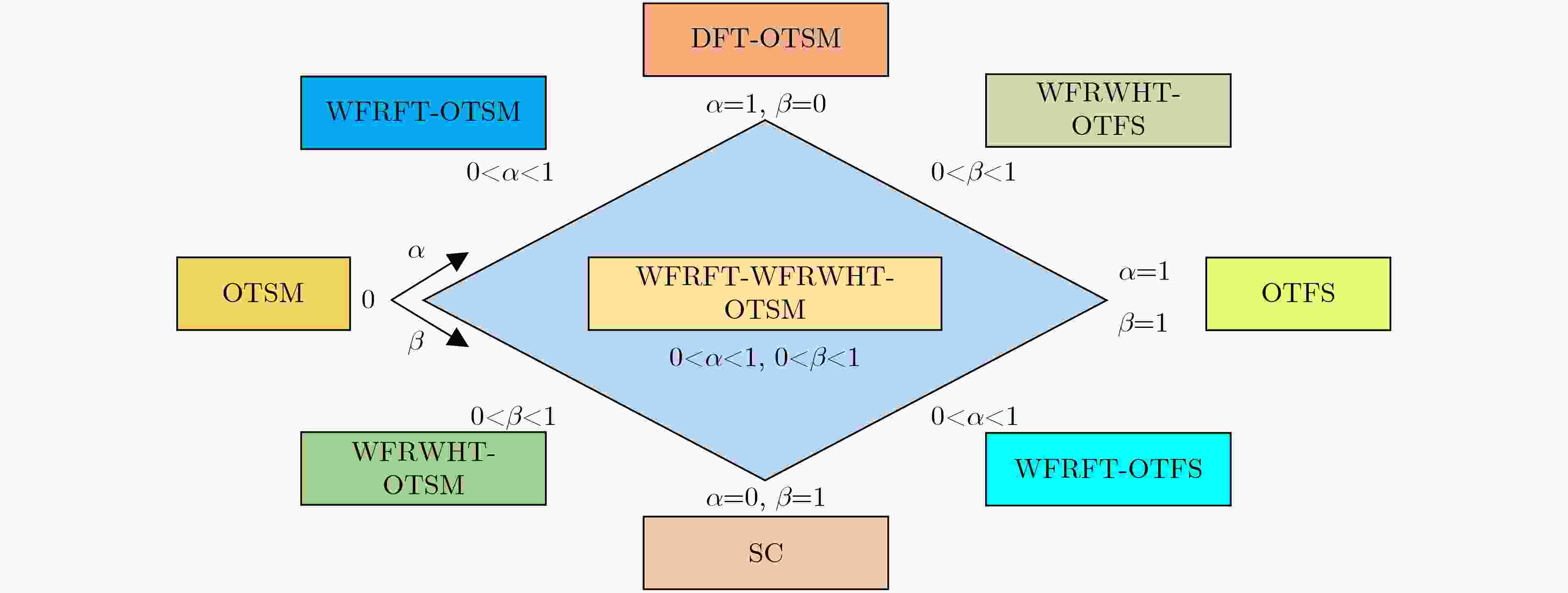
表 1 WFRFT-WFRWHT-OTSM的参数与表征波形关系
变量参数 载波体制 $\alpha = 0$, $\beta = 0$ OTSM $\alpha = 0$, $0 < \beta < 1$ WFRWHT-OTSM $\alpha = 0$, $\beta = {\text{1}}$ SC $0 < \alpha < {\text{1}}$, $\beta = 0$ WFRFT-OTSM $0 < \alpha < {\text{1}}$, $0 < \beta < 1$ WFRFT-WFRWHT-OTSM $0 < \alpha < {\text{1}}$, $\beta = {\text{1}}$ WFRFT-OTFS $\alpha = {\text{1}}$, $\beta = 0$ DFT-OTSM $\alpha = {\text{1}}$, $0 < \beta < 1$ WFRWHT-OTFS $\alpha = {\text{1}}$, $\beta = {\text{1}}$ OTFS -
[1] LIU An, HUANG Zhe, LI Min, et al. A survey on fundamental limits of integrated sensing and communication[J]. IEEE Communications Surveys & Tutorials, 2022, 24(2): 994–1034. doi: 10.1109/COMST.2022.3149272. [2] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. 2017 IEEE Wireless Communications and Networking Conference, San Francisco, USA, 2017: 1–6. [3] RAVITEJA P, HONG Yi, VITERBO E, et al. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 957–961. doi: 10.1109/TVT.2018.2878891. [4] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Orthogonal time-frequency space modulation: A promising next-generation waveform[J]. IEEE Wireless Communications, 2021, 28(4): 136–144. doi: 10.1109/MWC.001.2000408. [5] WANG Zhenduo, LIU Zhipeng, SUN Zhiguo, et al. BER performance analysis of OTFS systems with power allocation[J]. China Communications, 2023, 20(1): 24–35. doi: 10.23919/JCC.2023.01.003. [6] ZOU Tingting, XU Wenjun, GAO Hui, et al. Low-complexity linear equalization for OTFS systems with rectangular waveforms[C]. 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, Canada, 2021: 1–6. [7] 蒋占军, 刘庆达, 张鈜, 等. 高速移动通信系统中OTFS分数多普勒信道估计加窗研究[J]. 电子与信息学报, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561.JIANG Zhanjun, LIU Qingda, ZHANG Hong, et al. Study on OTFS fractional Doppler channel estimation and windowing in high-speed mobile communication systems[J]. Journal of Electronics &Information Technology, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561. [8] 蒋占军, 刘庆达. 高速移动通信系统中OTFS信道估计算法研究[J]. 电子与信息学报, 2021, 43(10): 2878–2885. doi: 10.11999/JEIT200683.JIANG Zhanjun and LIU Qingda. Study on OTFS channel estimation algorithms in high-speed mobile communication systems[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2878–2885. doi: 10.11999/JEIT200683. [9] WANG Zhenduo, CHEN Xingyu, SUN Zhiguo, et al. On the performance of nonlinear corrective active constellation expansion in OTFS systems[J]. IEEE Communications Letters, 2022, 26(6): 1418–1422. doi: 10.1109/LCOMM.2022.3165191. [10] QU Huiyang, LIU Guanghui, ZHANG Lei, et al. Low-complexity symbol detection and interference cancellation for OTFS system[J]. IEEE Transactions on Communications, 2021, 69(3): 1524–1537. doi: 10.1109/TCOMM.2020.3043007. [11] THAJ T, VITERBO E, and HONG Yi. Orthogonal time sequency multiplexing modulation: Analysis and low-complexity receiver design[J]. IEEE Transactions on Wireless Communications, 2021, 20(12): 7842–7855. doi: 10.1109/TWC.2021.3088479. [12] 李国军, 龙锟, 叶昌荣, 等. 高速移动环境下低复杂度OTSM迭代rake均衡方法[J]. 通信学报, 2022, 43(10): 86–93. doi: 10.11959/j.issn.1000-436x.2022203.LI Guojun, LONG Kun, YE Changrong, et al. Iterative rake equalization method for low-complexity OTSM in high-speed mobile environment[J]. Journal on Communications, 2022, 43(10): 86–93. doi: 10.11959/j.issn.1000-436x.2022203. [13] 李国军, 龙锟, 叶昌荣, 等. 高速移动环境下OTSM迭代检测算法研究[J]. 电子与信息学报, 2023, 45(6): 2098–2104. doi: 10.11999/JEIT220541.LI Guojun, LONG Kun, YE Changrong, et al. Research on OTSM iterative detection algorithm in high-speed mobile environment[J]. Journal of Electronics &Information Technology, 2023, 45(6): 2098–2104. doi: 10.11999/JEIT220541. [14] MEI Lin, SHA Xuejun, and ZHANG Naitong. The approach to carrier scheme convergence based on 4-weighted fractional Fourier transform[J]. IEEE Communications Letters, 2010, 14(6): 503–505. doi: 10.1109/LCOMM.2010.06.092413. [15] MEI Lin, XIAO Jiang, FANG Xiaojie, et al. Hybrid carrier and STBC based impulsive noise suppression for substation communications[C]. 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, Canada, 2020: 1–5. [16] MEI Lin, FANG Xiaojie, LIN Xu, et al. A WFRFT-based cyclic prefix-free hybrid-carrier FDE scheme[C]. 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 2020: 1–6. [17] WANG Zhenduo, CHEN Xingyu, and NING Xiaoyan. BER analysis of integrated WFRFT-OTFS waveform framework over static multipath channels[J]. IEEE Communications Letters, 2021, 25(3): 754–758. doi: 10.1109/LCOMM.2020.3040822. [18] MALLAIAH R and MANI V V. A novel OTFS system based on DFrFT-OFDM[J]. IEEE Wireless Communications Letters, 2022, 11(6): 1156–1160. doi: 10.1109/LWC.2022.3159534. [19] LIN Xu, MEI Lin, LABEAU F, et al. Efficient fast-convolution based hybrid carrier system[J]. IEEE Transactions on Wireless Communications, 2022, 21(5): 3508–3522. doi: 10.1109/TWC.2021.3122880. [20] VAN LOAN C F. The ubiquitous Kronecker product[J]. Journal of Computational and Applied Mathematics, 2000, 123(1/2): 85–100. doi: 10.1016/S0377-0427(00)00393-9. [21] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276. -





 下载:
下载:


 下载:
下载:
