基于深度学习的下行大规模MIMO OFDM系统的1比特预编码算法

周宸颢; 温利嫄; 钱骅; 康凯

doi:10.11999/JEIT230239

基于深度学习的下行大规模MIMO OFDM系统的1比特预编码算法

doi: 10.11999/JEIT230239

周宸颢^{1, 2},
温利嫄^{1, 2, 3},
钱骅¹,
康凯^1, ,

1.
中国科学院上海高等研究院上海 201210
2.
中国科学院大学北京 100049
3.
上海科技大学信息科学与技术学院上海 201210

基金项目: 国家重点研究发展计划(2020YFB2205603) ，国家自然科学基金(61971286)

详细信息

作者简介:
周宸颢：男，博士生，研究方向为无线通信

温利嫄：女，博士生，研究方向为无线通信

钱骅：男，研究员，研究方向为无线通信、非线性信号处理、大数据信号处理

康凯：男，正高级工程师，研究方向为无线通信、通信系统设计、物联网技术

通讯作者:
康凯　kangk@sari.ac.cn

中图分类号: TN929.5; TP181
计量
- 文章访问数: 537
- HTML全文浏览量: 242
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2023-07-18
- 修回日期: 2023-10-23
- 网络出版日期: 2023-10-27
- 刊出日期: 2024-03-27

1-bit Precoding Algorithm for Massive MIMO OFDM Downlink Systems with Deep Learning

ZHOU Chenhao^{1, 2},
WEN Liyuan^{1, 2, 3},
QIAN Hua¹,
KANG Kai^{1
, ,}

1.
Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201210, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
School of Information Science and Technology, ShanghaiTech University, Shanghai 201210, China

Funds: The National Key Research and Development Program of China (2020YFB2205603),The National Natural Science Foundation of China (61971286)

摘要

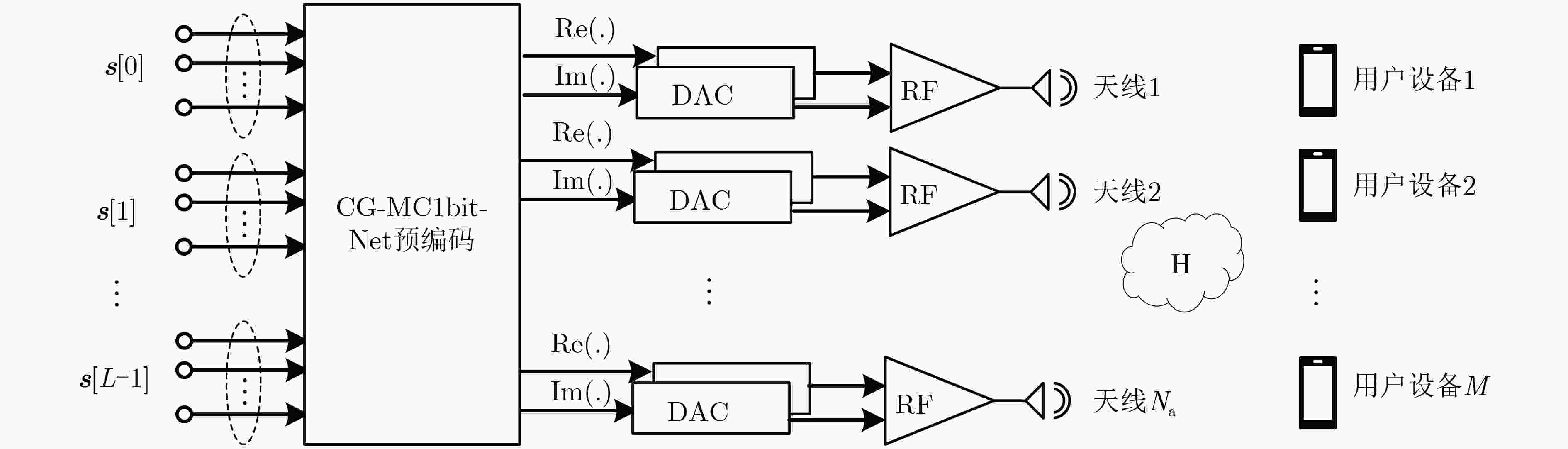
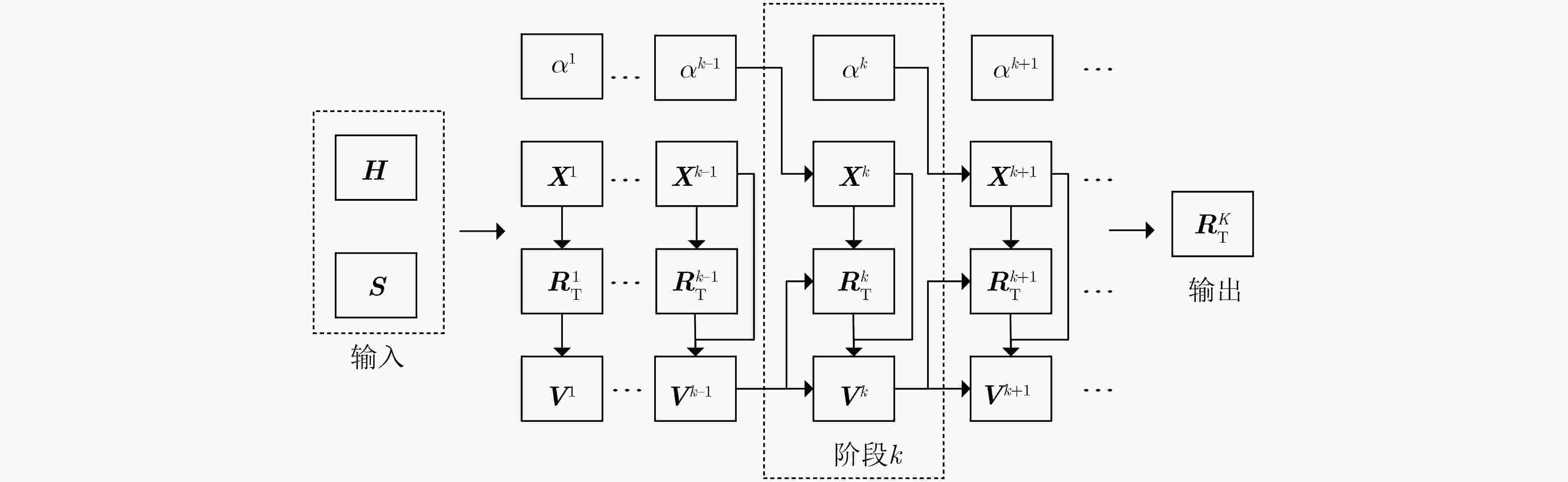
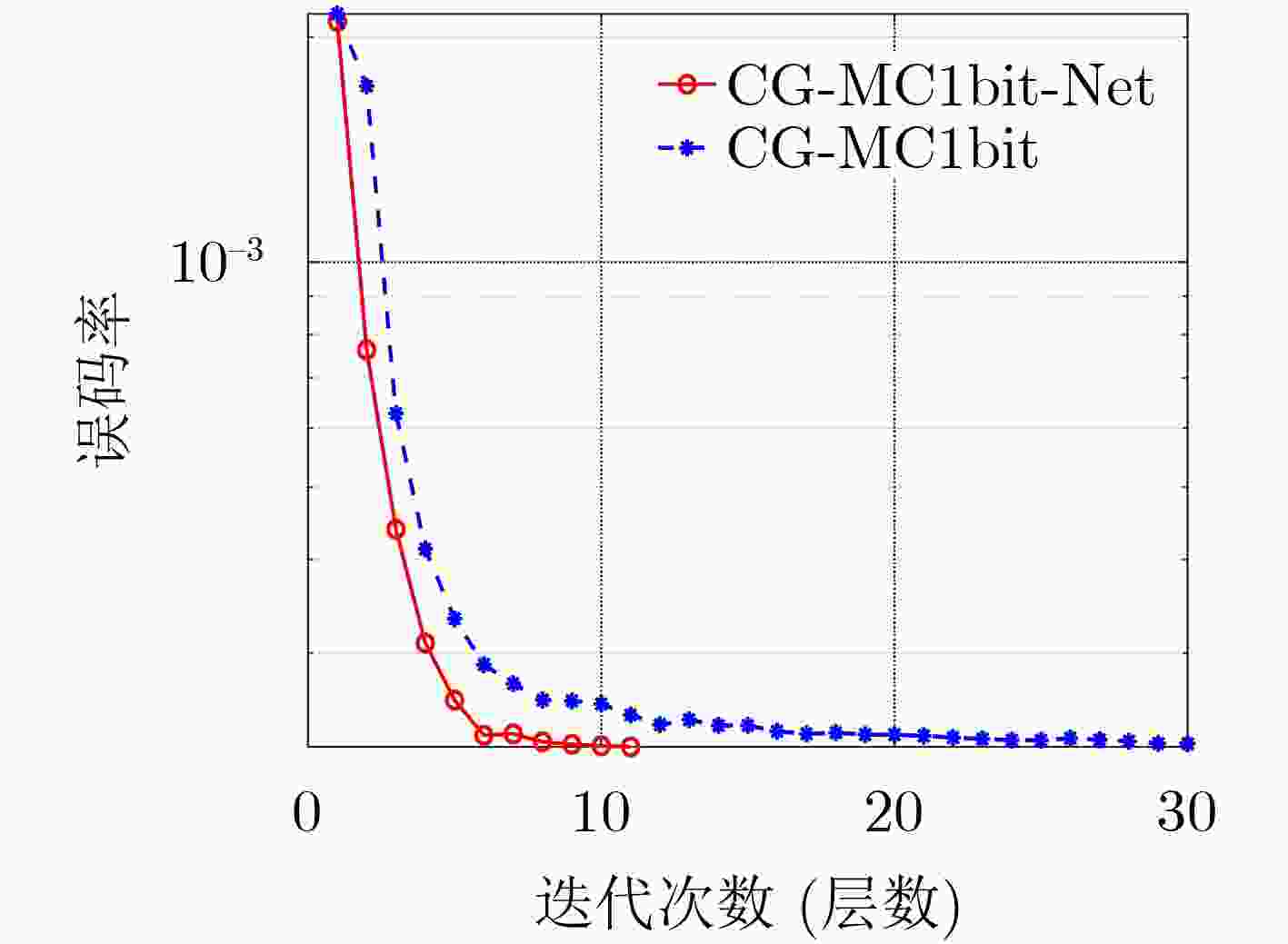
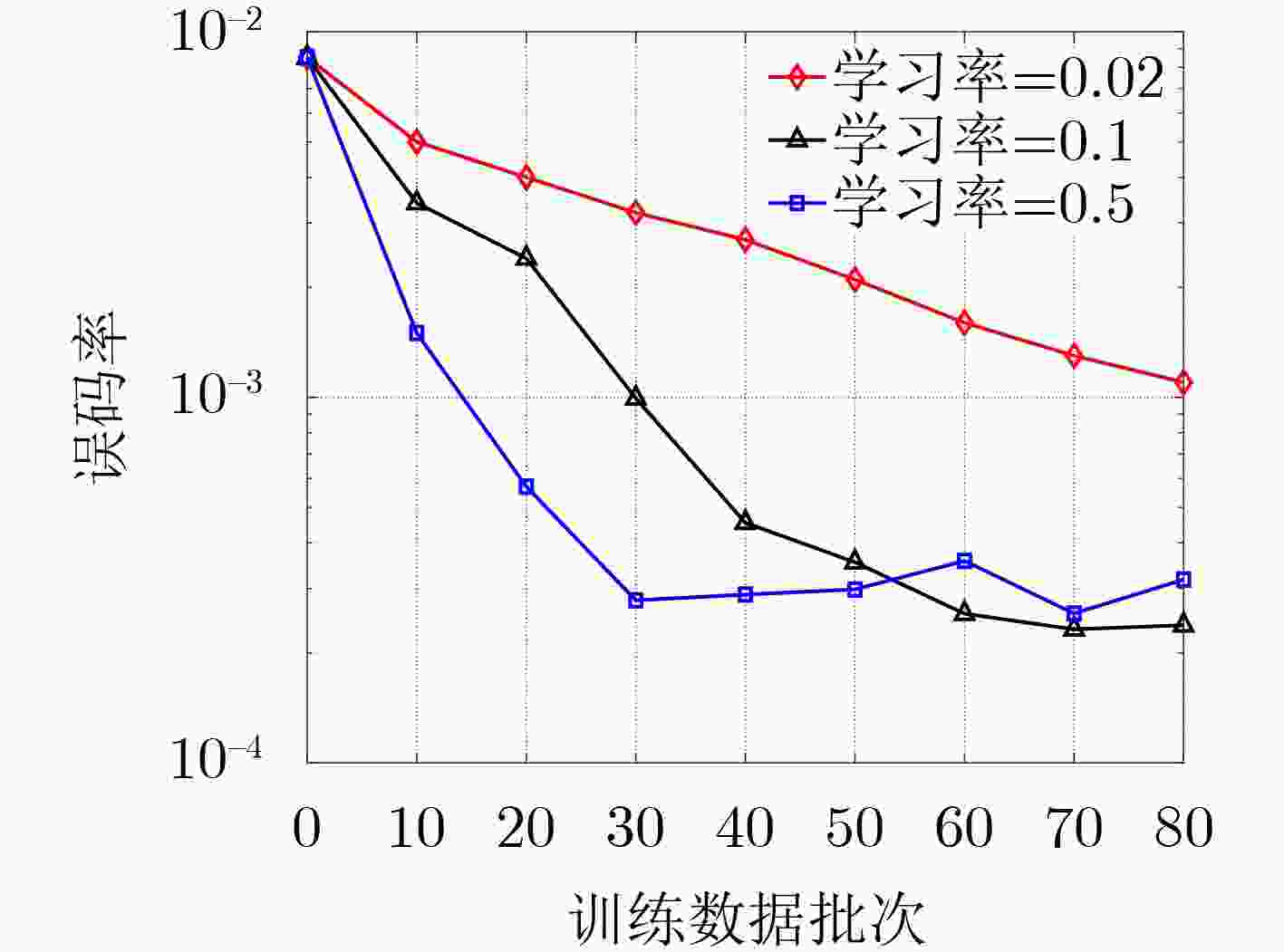
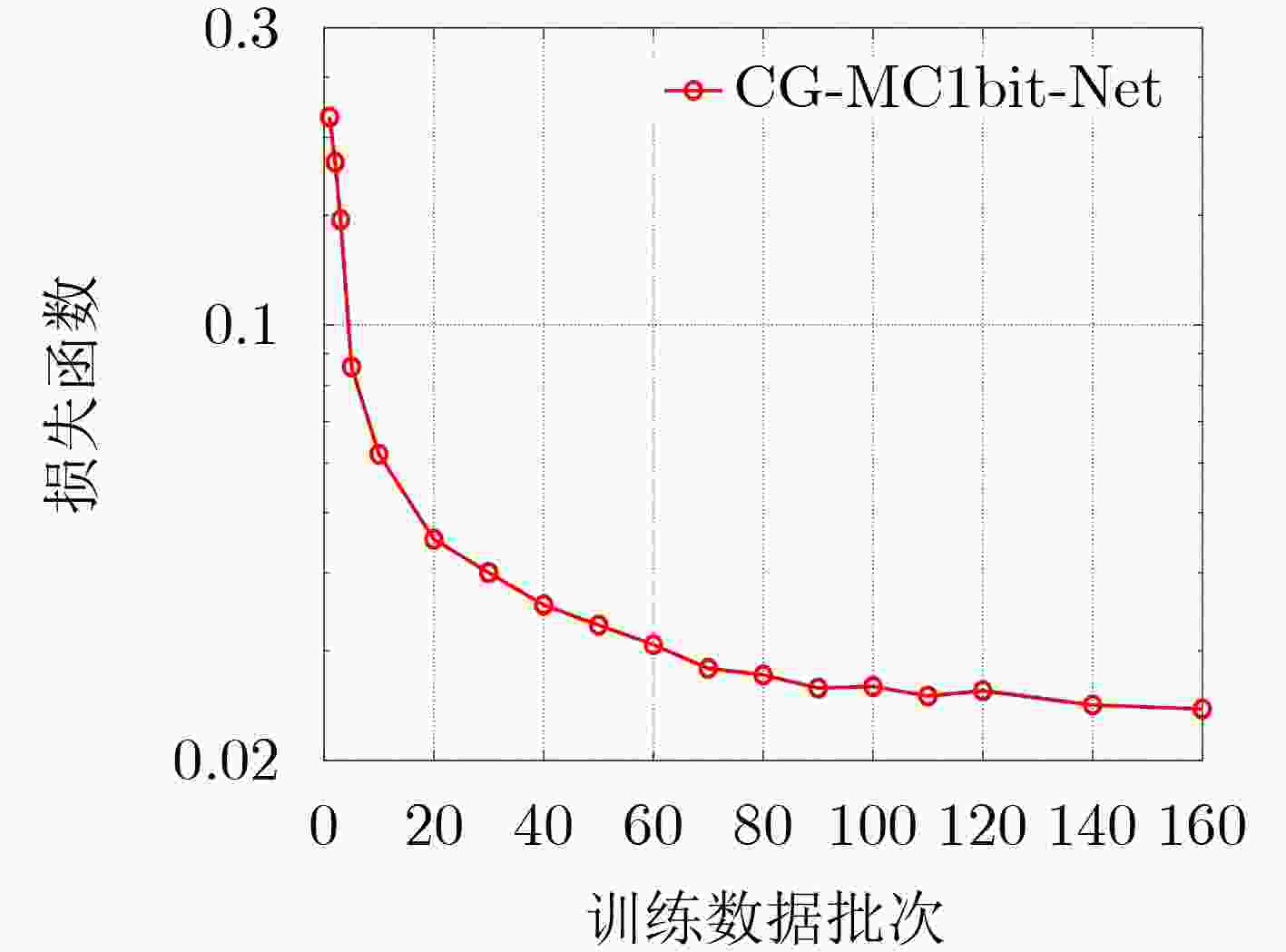
摘要: 大规模多输入多输出(MIMO)系统中通过在基站端配备数百根天线，在提高频谱利用效率的同时，也带来了系统成本的增加。本课题组之前提出了一种适用于下行大规模MIMO正交频分复用(OFDM)系统的收敛保证的多载波1比特预编码算法(CG-MC1bit)，能够获得较优的系统性能，但相应的计算复杂度较高，阻碍了其在实时系统中的应用。为进一步解决大规模MIMO系统中的成本和功耗问题，该文提出了一个模型驱动的神经网络，在CG-MC1bit算法的基础上迭代展开(Unfolding)得到了一种更加高效的CG-MC1bit-Net算法。具体而言，将迭代算法展开为一个神经网络，并引入可训练的参数来替代前向传播中的高复杂性操作。实验结果表明，该方法能够自动更新参数，与传统的预编码算法相比，收敛速度更快，计算复杂度更低。
- 大规模多输入多输出 /
- 预编码 /
- 正交频分复用(OFDM) /
- 迭代展开 /
- 神经网络
Abstract: The base station of a massive Multiple-Input Multiple-Output (MIMO) system is equipped with hundreds of antennas, enhancing the spectral efficiency of the system and increasing the system costs. To address this problem, our research group proposed a Convergence-Guaranteed Multi-Carrier one-bit precoding (CG-MC1bit) iterative algorithm suitable for Orthogonal Frequency-Division Multiplexing (OFDM) downlink massive MIMO systems, which can ensure superior system performance. However, the corresponding computational complexity is high, hindering the practical application of the algorithm in real-time systems. To address this issue, we propose a model-driven, unfolding neural network, which is based on the CG-MC1bit iterative algorithm and introduces trainable parameters to replace high-complexity operations in forward propagation. In particular, we unfold the iterative algorithm into a neural network and introduce trainable parameters to replace high-complexity operations in forward propagation. Simulation results reveal that this method can automatically update parameters. In addition, compared with the traditional precoding algorithms, the proposed method has a higher convergence speed and lower computational complexity.
- Massive MIMO /
- Precoding /
- Orthogonal Frequency-Division Multiplexing(OFDM) /
- Unfolding /
- Neural Network

HTML全文

图 1 系统模型

下载: 全尺寸图片幻灯片

图 2 数据流图

下载: 全尺寸图片幻灯片

图 3 CG-MC1bit与CG-MC1bit-Net算法收敛性对比

下载: 全尺寸图片幻灯片

图 4 不同学习率下的收敛速度

下载: 全尺寸图片幻灯片

图 5 损失函数的下降趋势

下载: 全尺寸图片幻灯片

图 6 当$ M = {\text{8 , }}{N_{\text{a}}} = {\text{128}} $时各算法的误码率性能对比

下载: 全尺寸图片幻灯片

图 7 当$ M = {\text{8 , }}{N_{\text{a}}} = {\text{512}} $时各算法的误码率性能对比

下载: 全尺寸图片幻灯片

图 8 当$ {\text{ }}{N_{\text{a}}} = {\text{128}} $时不同用户数的误码率性能对比

下载: 全尺寸图片幻灯片

1 CG-MC1bit-Net算法

已知：传输信号矩阵$ {{\boldsymbol{S}}} $，信道矩阵$ {{\boldsymbol{H}}} $，神经网络层数$ K $
1) 初始化 $ {\boldsymbol{X}}^{\text{0}}={{\bf{1}}},\;{\boldsymbol{R}}^{\text{0}}\text{=}{{\bf{1}}},\;{\boldsymbol{V}}^{\text{0}}={{ {\textit{0}}}},\;\alpha =\text{0}\text{.1} $
2) for 数据集中的每个样本 do
3) 　初始化$k = {\text{0}}$
4) 　while $k < K$ do
5) 　　${\tilde {\boldsymbol{H}}} = {\alpha ^k}{{\boldsymbol{H}}}$
6) 　　初始化$l = {\text{0}}$
7) 　　for $l < L$ do
8) 　　　根据式(4)更新$ {{{\boldsymbol{x}}}^{k + 1}}[l] $，$ l = l + {\text{1}} $
9) 　　end for
10) 　 $ {{\boldsymbol{R}}}_{\text{T}}^{k + 1} = \eta \tanh \left[ {\delta \dfrac{1}{L}\left( {{{{\boldsymbol{X}}}^{k + 1}} + \dfrac{1}{\lambda }{{{\boldsymbol{V}}}^k}} \right){{\boldsymbol{F}}}_L^{\text{H}}} \right] $
11) 　 $ {{{\boldsymbol{R}}}^{k + 1}} = {{\boldsymbol{R}}}_{\text{T}}^{k + 1}{{{\boldsymbol{F}}}_L} $
12) 　 $ {{{\boldsymbol{V}}}^{k + 1}} = {{{\boldsymbol{V}}}^k} + \lambda \left( {{{\boldsymbol{X}}}_{\text{T}}^{k + 1} - {{{\boldsymbol{R}}}^{k + 1}}} \right) $
13) 　 $ k = k + {\text{1}} $
14) 　end while
15) 　输出$ {{\boldsymbol{R}}}_{\text{T}}^K $，并根据式(11)计算损失函数$ {\text{los}}{{\text{s}}_{{\text{MSE}}}} $
16) 　执行会话
17) 　for 隐藏层或输出层的每个神经元 do
18) 　更新网络中的每一个权值和偏差
19) 　end for
20) end for

下载: 导出CSV

表 1 运行速度对比

预编码算法	天线数128	天线数512
CG-MC1bit-Net	0.429 s	2.127 s
CG-MC1bitx	3.47 s	10.33 s

下载: 导出CSV

参考文献(22)

[1]	BJÖRNSON E, SANGUINETTI L, HOYDIS J, et al. Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer?[J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3059–3075. doi: 10.1109/TWC.2015.2400437.
[2]	LU Lu, LI G Y, SWINDLEHURST A L, et al. An overview of massive MIMO: Benefits and challenges[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 742–758. doi: 10.1109/jstsp.2014.2317671.
[3]	RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: Opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40–60. doi: 10.1109/msp.2011.2178495.
[4]	SAXENA A K, FIJALKOW I, MEZGHANI A, et al. Analysis of one-bit quantized ZF precoding for the multiuser massive MIMO downlink[C]. 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2016: 758–762. doi: 10.1109/ACSSC.2016.7869148.
[5]	SWINDLEHURST A L, SAXENA K A, MEZGHANI A, et al. Minimum probability-of-error perturbation precoding for the one-bit massive MIMO downlink[C]. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, USA, 2017: 6483–6487. doi: 10.1109/ICASSP.2017.7953405.
[6]	CHU Lei, WEN Fei, LI L, et al. Efficient nonlinear precoding for massive MIMO downlink systems with 1-bit DACs[J]. IEEE Transactions on Wireless Communications, 2019, 18(9): 4213–4224. doi: 10.1109/TWC.2019.2920125.
[7]	CHEN Zhenhui, WANG Yajun, LIAN Zhuxian, et al. Low-complexity constant envelope precoding with one-bit DAC for massive MU-MIMO systems[J]. IEEE Wireless Communications Letters, 2021, 10(12): 2805–2809. doi: 10.1109/LWC.2021.3118202.
[8]	HAQIQATNEJAD A, KAYHAN F, SHAHBAZPANAHI S, et al. Finite-alphabet symbol-level multiuser precoding for massive MU-MIMO downlink[J]. IEEE Transactions on Signal Processing, 2021, 69: 5595–5610. doi: 10.1109/TSP.2021.3113803.
[9]	JACOBSSON S, CASTAÑEDA O, JEON C, et al. Nonlinear precoding for phase-quantized constant-envelope massive MU-MIMO-OFDM[C]. 2018 25th International Conference on Telecommunications (ICT), Saint-Malo, France, 2018: 367–372. doi: 10.1109/ICT.2018.8464896.
[10]	TSINOS C G, DOMOUCHTSIDIS S, CHATZINOTAS S, et al. Symbol level precoding with low resolution DACs for constant envelope OFDM MU-MIMO systems[J]. IEEE Access, 2020, 8: 12856–12866. doi: 10.1109/ACCESS.2019.2963857.
[11]	WEN Liyuan, QIAN Hua, HU Yunbo, et al. One-bit Downlink precoding for massive MIMO OFDM system[J]. IEEE Transactions on Wireless Communications, 2023, 22(9): 5914–5926. doi: 10.1109/TWC.2023.3238380.
[12]	ZHANG Shangwei, LIU Jiajia, RODRIGUES T K, et al. Deep learning techniques for advancing 6G communications in the physical layer[J]. IEEE Wireless Communications, 2021, 28(5): 141–147. doi: 10.1109/MWC.001.2000516.
[13]	LIU Zhenyu, DEL ROSARIO M, and DING Zhi. A Markovian model-driven deep learning framework for massive MIMO CSI feedback[J]. IEEE Transactions on Wireless Communications, 2022, 21(2): 1214–1228. doi: 10.1109/TWC.2021.3103120.
[14]	ZHANG Xinliang and VAEZI Mojtaba. Multi-objective DNN-based precoder for MIMO communications[J]. IEEE Transactions on Communications, 2021, 69(7): 4476–4488. doi: 10.1109/TCOMM.2021.3071536.
[15]	HE Hengtao, ZHANG Mengjiao, JIN Shi, et al. Model-driven deep learning for massive MU-MIMO with finite-alphabet precoding[J]. IEEE Communications Letters, 2020, 24(10): 2216–2220. doi: 10.1109/LCOMM.2020.3002082.
[16]	BALATSOUKAS-STIMMING A, CASTAÑEDA O, JACOBSSON S, et al. Neural-network optimized 1-bit precoding for massive MU-MIMO[C]. 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2019: 1–5. doi: 10.1109/SPAWC.2019.8815519.
[17]	HU Qiyu, CAI Yunlong, SHI Qingjiang, et al. Iterative algorithm induced deep-unfolding neural networks: Precoding design for multiuser MIMO systems[J]. IEEE Transactions on Wireless Communications, 2021, 20(2): 1394–1410. doi: 10.1109/TWC.2020.3033334.
[18]	蒋伊琳, 尹子茹, 宋宇. 基于卷积神经网络的低截获概率雷达信号检测算法[J]. 电子与信息学报, 2022, 44(2): 718–725. doi: 10.11999/JEIT210132. JIANG Yilin, YIN Ziru, and SONG Yu. Low probability of intercept radar signal detection algorithm based on convolutional neural networks[J]. Journal of Electronics & Information Technology, 2022, 44(2): 718–725. doi: 10.11999/JEIT210132.
[19]	ZHANG Kai, VAN GOOL L, and TIMOFTE R. Deep unfolding network for image super-resolution[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 2020: 3214–3223. doi: 10.1109/CVPR42600.2020.00328.
[20]	SAMUEL N, DISKIN T, and WIESEL A. Deep MIMO detection[C]. 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 2017: 1–5. doi: 10.1109/SPAWC.2017.8227772.
[21]	HUBARA I, COURBARIAUX M, SOUDRY D, et al. Binarized neural networks[C]. Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook, USA, 2016: 4114–4122.
[22]	QIN Haotong, GONG Ruihao, LIU Xianglong, et al. Forward and backward information retention for accurate binary neural networks[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 2247–2256. doi: 10.1109/CVPR42600.2020.00232.