Satellite Image Encryption Algorithm Based on Chaos Theory and DNA Dynamic Coding
-
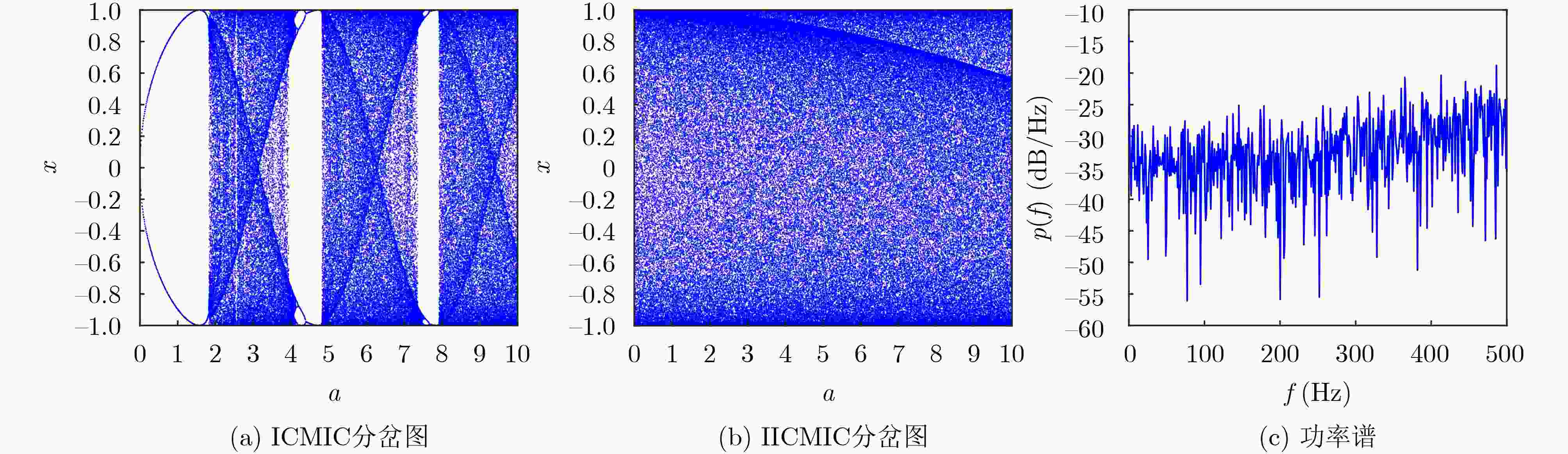
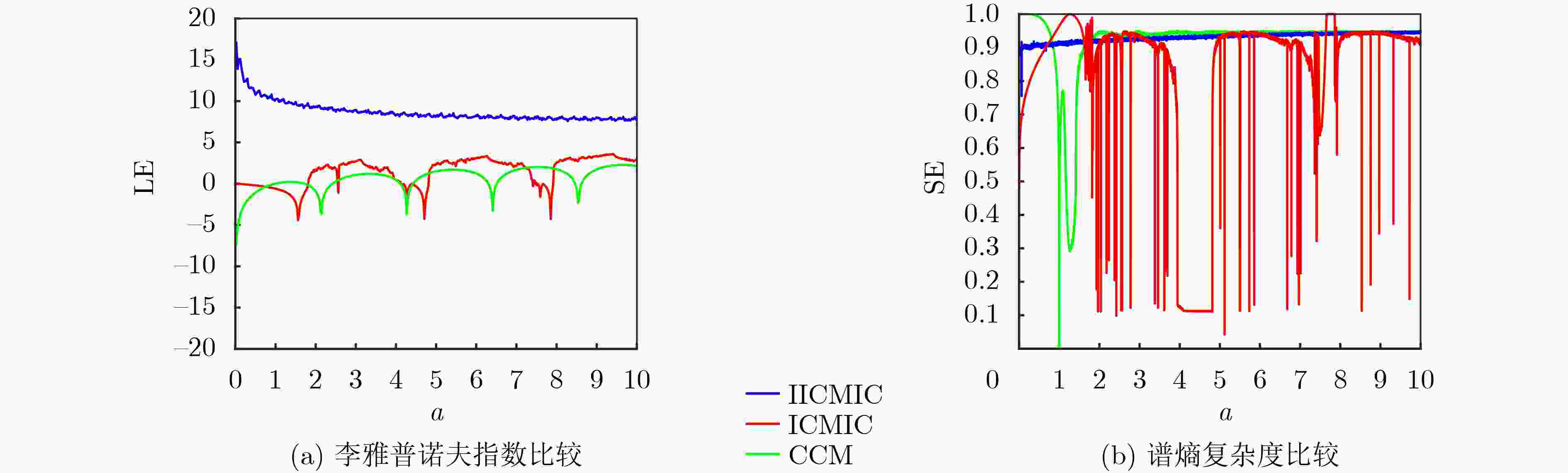
摘要: 针对卫星图像在传输、存储过程中涉及的信息安全问题,该文提出一种新型的基于混沌理论与DNA动态编码的卫星图像加密算法。首先,提出一种改进型无限折叠混沌映射,拓宽了原有无限折叠混沌映射的混沌区间。之后,结合改进型Chebyshev混沌映射与SHA-256哈希算法,生成加密算法的密钥流,提升算法的明文敏感性。然后,利用混沌系统的状态值对Hilbert局部置乱后的像素进行DNA编码,实现DNA动态编码,解决了DNA编码规则较少所带来的容易受到暴力攻击的弱点。最后,使用混沌序列完成进一步混沌加密,从而彻底混淆原始像素信息,增加加密算法的随机性与复杂性,得到密文图像。实验结果表明,该算法具有较好的加密效果和应对各种攻击的能力。Abstract: Considering the information security problems involved in the transmission and storage of satellite images, a new satellite image encryption algorithm based on chaos theory and DNA dynamic coding is proposed. Firstly, an improved infinite folding chaotic map is proposed, which broadens the chaotic interval of the original infinite folding chaotic map. Then, combined with the improved Chebyshev chaotic map and SHA-256 hash algorithm, the key stream of the encryption algorithm is generated to improve the plaintext sensitivity of the algorithm. Then, the state value of the chaotic system is used to encode the pixels after Hilbert local scrambling to realize DNA dynamic coding, which solves the weakness of being vulnerable to violent attacks caused by fewer DNA coding rules. Finally, the chaotic sequence is used to complete further chaotic encryption, to completely confuse the original pixel information, increase the randomness and complexity of the encryption algorithm, and obtain the ciphertext image. The experimental results show that the algorithm has a better encryption effect and the ability to deal with various attacks.
-
Key words:
- Satellite image encryption /
- Chaos theory /
- DNA dynamic coding /
- Hash algorithm
-
表 1 本文算法与部分数字图像加密算法分析对比
表 2 本文算法与部分卫星图像加密算法分析对比
表 3 相关系数分析
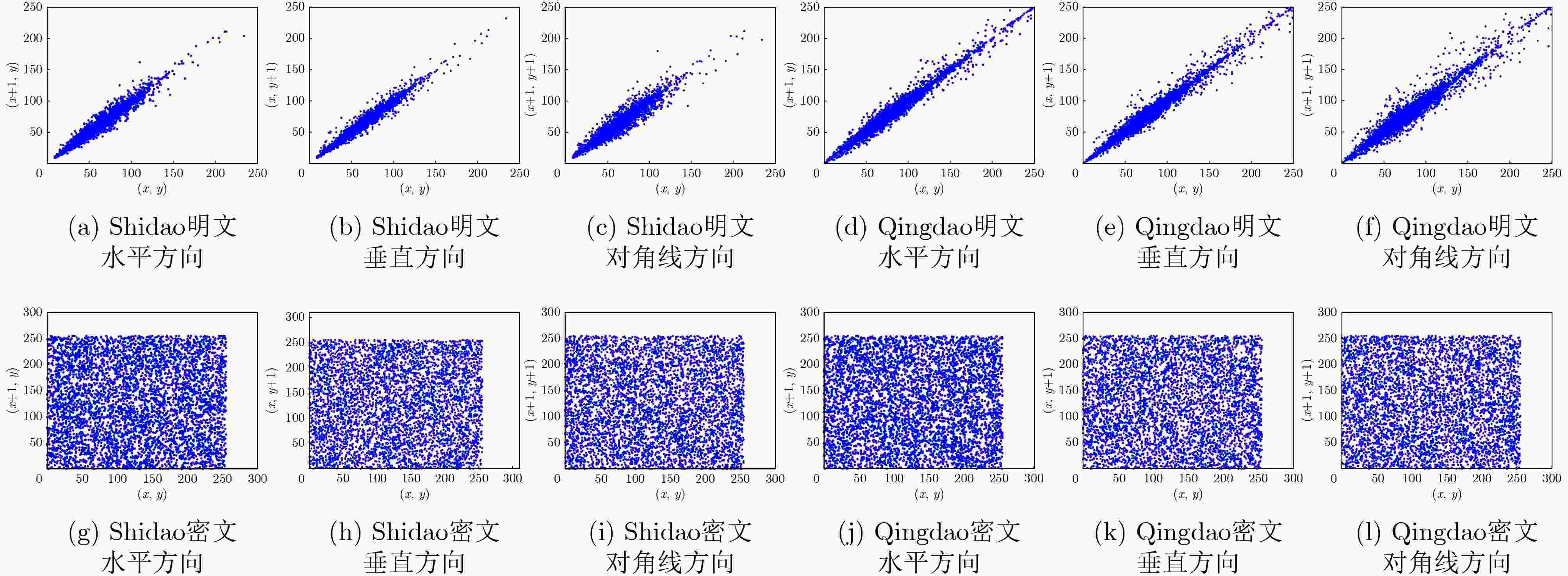
卫星图像 明文图像 密文图像 水平方向 垂直方向 对角线方向 水平方向 垂直方向 对角线方向 Shidao 0.990 2 0.987 6 0.977 1 0.019 7 –0.004 8 –0.003 5 Qingdao 0.986 1 0.989 9 0.974 1 0.010 4 –0.010 8 –0.016 5 表 4 信息熵分析
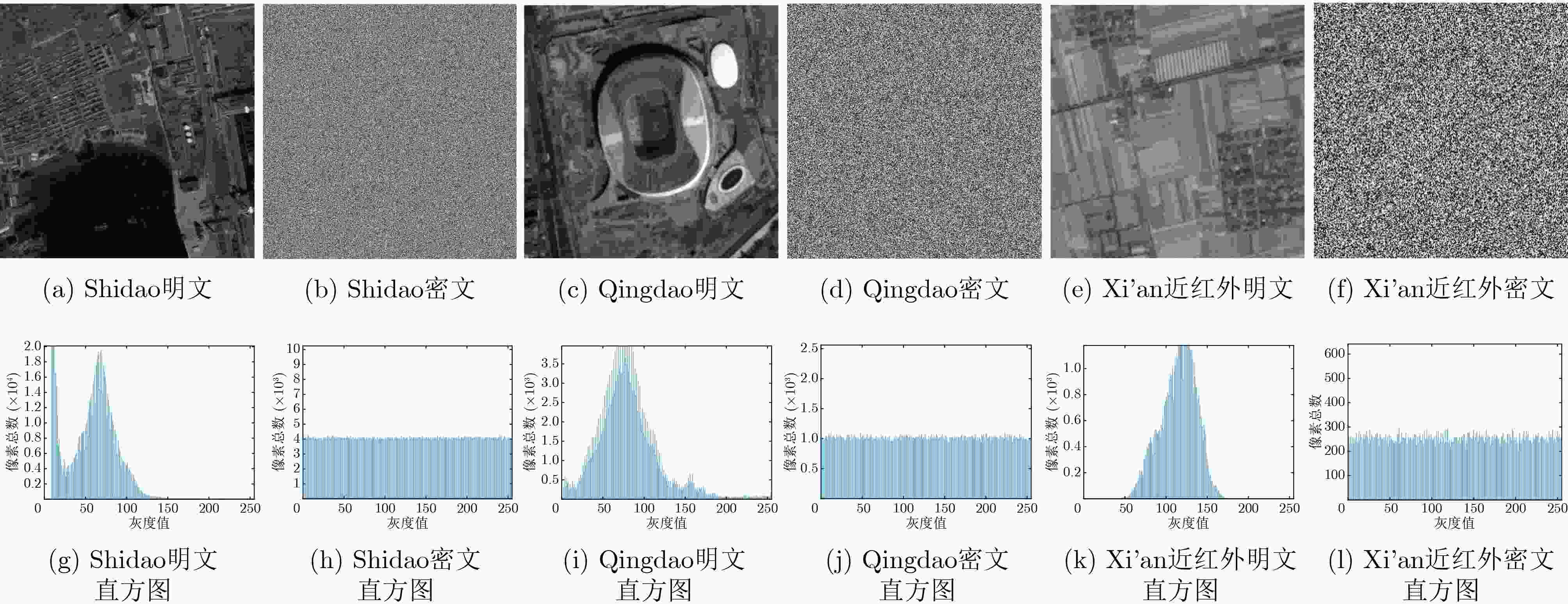
卫星图像 明文图像信息熵 密文图像信息熵 Qingdao 7.106 4 7.999 3 Xi'an近红外波段 6.447 7 7.996 9 表 5 视觉与无损分析
测试图像 PSNR SSIM PSNR SSIM Lena 8.561 1 0.008 9 ∞ 1 Shidao 7.471 4 0.007 4 ∞ 1 Qingdao 8.517 9 0.009 4 ∞ 1 -
[1] LIU Zhanqiang, WANG Licheng, WANG Xianmin, et al. Secure remote sensing image registration based on compressed sensing in cloud setting[J]. IEEE Access, 2019, 7: 36516–36526. doi: 10.1109/ACCESS.2019.2903826. [2] NAIM M, ALI PACHA A, and SERIEF C. A novel satellite image encryption algorithm based on hyperchaotic systems and Josephus problem[J]. Advances in Space Research, 2021, 67(7): 2077–2103. doi: 10.1016/j.asr.2021.01.018. [3] BENTOUTOU Y, BENSIKADDOUR E H, TALEB N, et al. An improved image encryption algorithm for satellite applications[J]. Advances in Space Research, 2020, 66(1): 176–192. doi: 10.1016/j.asr.2019.09.027. [4] CHEN Junxin, ZHU Zhiliang, FU Chong, et al. An efficient image encryption scheme using lookup table-based confusion and diffusion[J]. Nonlinear Dynamics, 2015, 81(3): 1151–1166. doi: 10.1007/s11071-015-2057-6. [5] HU Guiqiang, XIAO Di, WANG Yong, et al. Cryptanalysis of a chaotic image cipher using Latin square-based confusion and diffusion[J]. Nonlinear Dynamics, 2017, 88(2): 1305–1316. doi: 10.1007/s11071-016-3311-2. [6] MONDAL B, KUMAR P, and SINGH S. A chaotic permutation and diffusion based image encryption algorithm for secure communications[J]. Multimedia Tools and Applications, 2018, 77(23): 31177–31198. doi: 10.1007/s11042-018-6214-z. [7] LI Ming, ZHOU Kanglei, REN Hua, et al. Cryptanalysis of permutation–diffusion-based lightweight chaotic image encryption scheme using CPA[J]. Applied Sciences, 2019, 9(3): 494. doi: 10.3390/app9030494. [8] DAWAHDEH Z E, YAAKOB S N, and AZIF BIN OTHMAN R. A new image encryption technique combining elliptic curve cryptosystem with hill cipher[J]. Journal of King Saud University - Computer and Information Sciences, 2018, 30(3): 349–355. doi: 10.1016/j.jksuci.2017.06.004. [9] LONE P N, SINGH D, STOFFOVÁ V, et al. Cryptanalysis and improved image encryption scheme using elliptic curve and affine hill cipher[J]. Mathematics, 2022, 10(20): 3878. doi: 10.3390/math10203878. [10] ANDONO P N and SETIADI D R I M. Improved pixel and bit confusion-diffusion based on mixed chaos and hash operation for image encryption[J]. IEEE Access, 2022, 10: 115143–115156. doi: 10.1109/ACCESS.2022.3218886. [11] KHAIRULLAH M K, ALKAHTANI A A, BAHARUDDIN M Z B, et al. Designing 1D chaotic maps for fast chaotic image encryption[J]. Electronics, 2021, 10(17): 2116. doi: 10.3390/electronics10172116. [12] JIANG Donghua, LIU Lidong, ZHU Liya, et al. Adaptive embedding: A novel meaningful image encryption scheme based on parallel compressive sensing and slant transform[J]. Signal Processing, 2021, 188: 108220. doi: 10.1016/j.sigpro.2021.108220. [13] ZHANG Xuncai, WANG Lingfei, ZHOU Zheng, et al. A chaos-based image encryption technique utilizing Hilbert curves and H-fractals[J]. IEEE Access, 2019, 7: 74734–74746. doi: 10.1109/ACCESS.2019.2921309. [14] SUN Junwei, MA Yongxing, WANG Zicheng, et al. Dynamic analysis and cryptographic application of a 5D hyperbolic memristor-coupled neuron[J]. Nonlinear Dynamics, 2023, 111(9): 8751–8769. doi: 10.1007/s11071-023-08237-9. [15] 徐锡统, 陈圣波, 于岩. 结合小波包变换与混沌神经元的遥感图像加密[J]. 遥感信息, 2021, 36(4): 76–83. doi: 10.3969/j.issn.1000-3177.2021.04.011.XU Xitong, CHEN Shengbo, and YU Yan. Remote sensing image encryption combining wavelet packet transform and chaotic neuron[J]. Remote Sensing Information, 2021, 36(4): 76–83. doi: 10.3969/j.issn.1000-3177.2021.04.011. [16] WANG Xingyuan, WANG Yu, ZHU Xiaoqiang, et al. Image encryption scheme based on chaos and DNA plane operations[J]. Multimedia Tools and Applications, 2019, 78(18): 26111–26128. doi: 10.1007/s11042-019-07794-9. [17] YILDIRIM M. DNA encoding for RGB image encryption with memristor based neuron model and chaos phenomenon[J]. Microelectronics Journal, 2020, 104: 104878. doi: 10.1016/j.mejo.2020.104878. [18] LI Xiang, WANG Leyuan, YAN Yinfa, et al. An improvement color image encryption algorithm based on DNA operations and real and complex chaotic systems[J]. Optik, 2016, 127(5): 2558–2565. doi: 10.1016/j.ijleo.2015.11.221. [19] CHAI Xiuli, CHEN Yiran, and BROYDE L. A novel chaos-based image encryption algorithm using DNA sequence operations[J]. Optics and Lasers in Engineering, 2017, 88: 197–213. doi: 10.1016/j.optlaseng.2016.08.009. [20] WANG Leimin, JIANG Shan, GE Mingfeng, et al. Finite-/fixed-time synchronization of memristor chaotic systems and image encryption application[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2021, 68(12): 4957–4969. doi: 10.1109/TCSI.2021.3121555. [21] WU Jiahui, LIAO Xiaofeng, and YANG Bo. Image encryption using 2D Hénon-Sine map and DNA approach[J]. Signal Processing, 2018, 153: 11–23. doi: 10.1016/j.sigpro.2018.06.008. [22] WU Chenyang, SUN Kehui, and XIAO Yan. A hyperchaotic map with multi-elliptic cavities based on modulation and coupling[J]. The European Physical Journal Special Topics, 2021, 230(7): 2011–2020. doi: 10.1140/epjs/s11734-021-00126-9. [23] 杨宣兵. 几类混沌系统特性分析、控制与图像加密应用研究[D]. [博士论文], 合肥工业大学, 2020.YANG Xuanbing. Characteristics analysis and control of several chaotic systems and their application in image encryption[D]. [Ph. D. dissertation], Hefei University of Technology, 2020. [24] FAN Shengwen, LI Kai, ZHANG Ying, et al. A hybrid chaotic encryption scheme for wireless body area networks[J]. IEEE Access, 2020, 8: 183411–183429. doi: 10.1109/ACCESS.2020.3029263. [25] 蒋东华, 朱礼亚, 沈子懿, 等. 结合二维压缩感知和混沌映射的双图像视觉安全加密算法[J]. 西安交通大学学报, 2022, 56(2): 139–148. doi: 10.7652/xjtuxb202202015.JIANG Donghua, ZHU Liya, SHEN Ziyi, et al. A double image visual security encryption algorithm combining 2D compressive sensing and chaotic mapping[J]. Journal of Xi'an Jiaotong University, 2022, 56(2): 139–148. doi: 10.7652/xjtuxb202202015. [26] 孙克辉, 贺少波, 何毅, 等. 混沌伪随机序列的谱熵复杂性分析[J]. 物理学报, 2013, 62(1): 010501. doi: 10.7498/aps.62.010501.SUN Kehui, HE Shaobo, HE Yi, et al. Complexity analysis of chaotic pseudo-random sequences based on spectral entropy algorithm[J]. Acta Physica Sinica, 2013, 62(1): 010501. doi: 10.7498/aps.62.010501. [27] ABBASI A A, MAZINANI M, and HOSSEINI R. Chaotic evolutionary-based image encryption using RNA codons and amino acid truth table[J]. Optics & Laser Technology, 2020, 132: 106465. doi: 10.1016/j.optlastec.2020.106465. [28] MAHMUD M, ATTA-UR-RAHMAN, LEE M, et al. Evolutionary-based image encryption using RNA codons truth table[J]. Optics & Laser Technology, 2020, 121: 105818. doi: 10.1016/j.optlastec.2019.105818. [29] CAO Chun, SUN Kehui, and LIU Wenhao. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map[J]. Signal Processing, 2018, 143: 122–133. doi: 10.1016/j.sigpro.2017.08.020. -





 下载:
下载:





 下载:
下载:
