Image Super-Resolution Algorithms Based on Deep Feature Differentiation Network
-
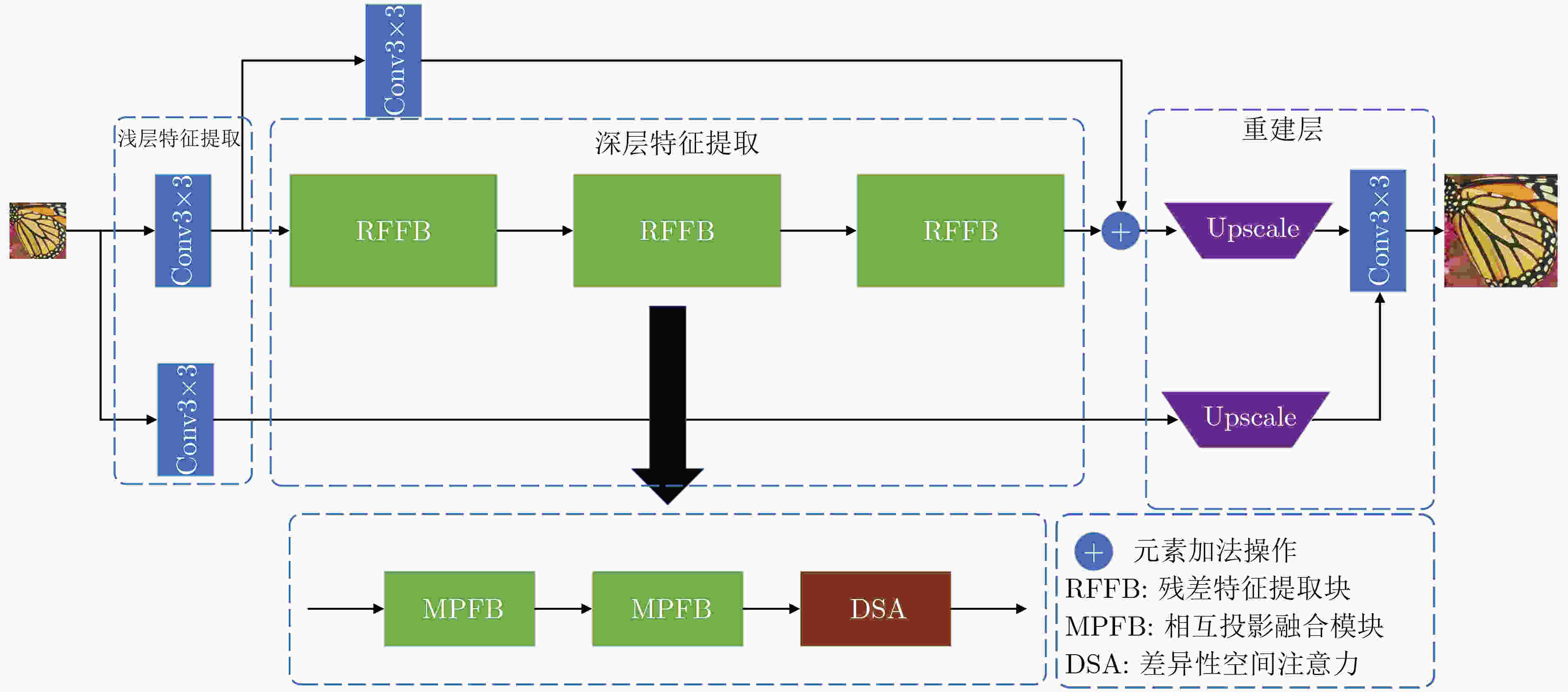
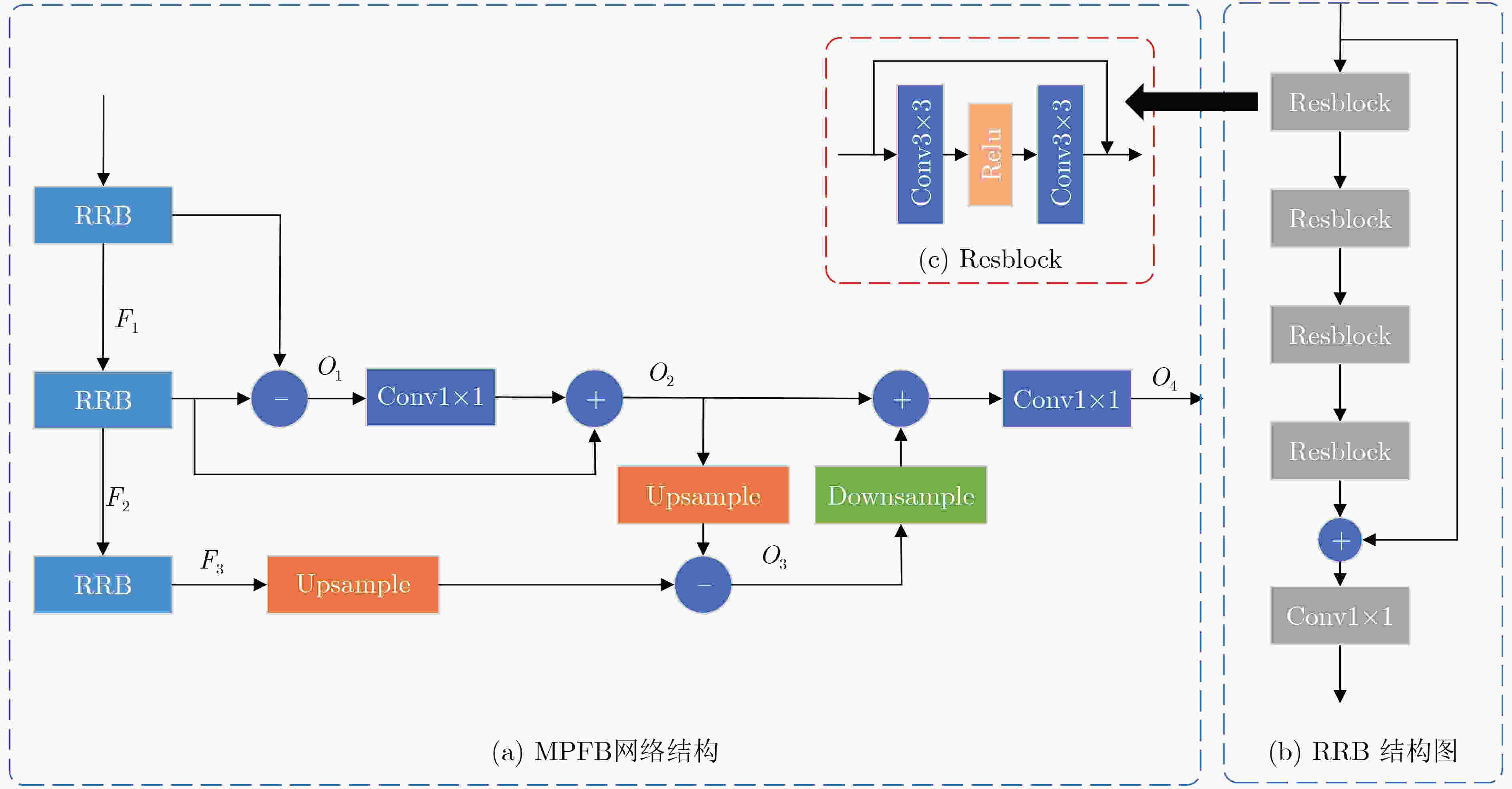
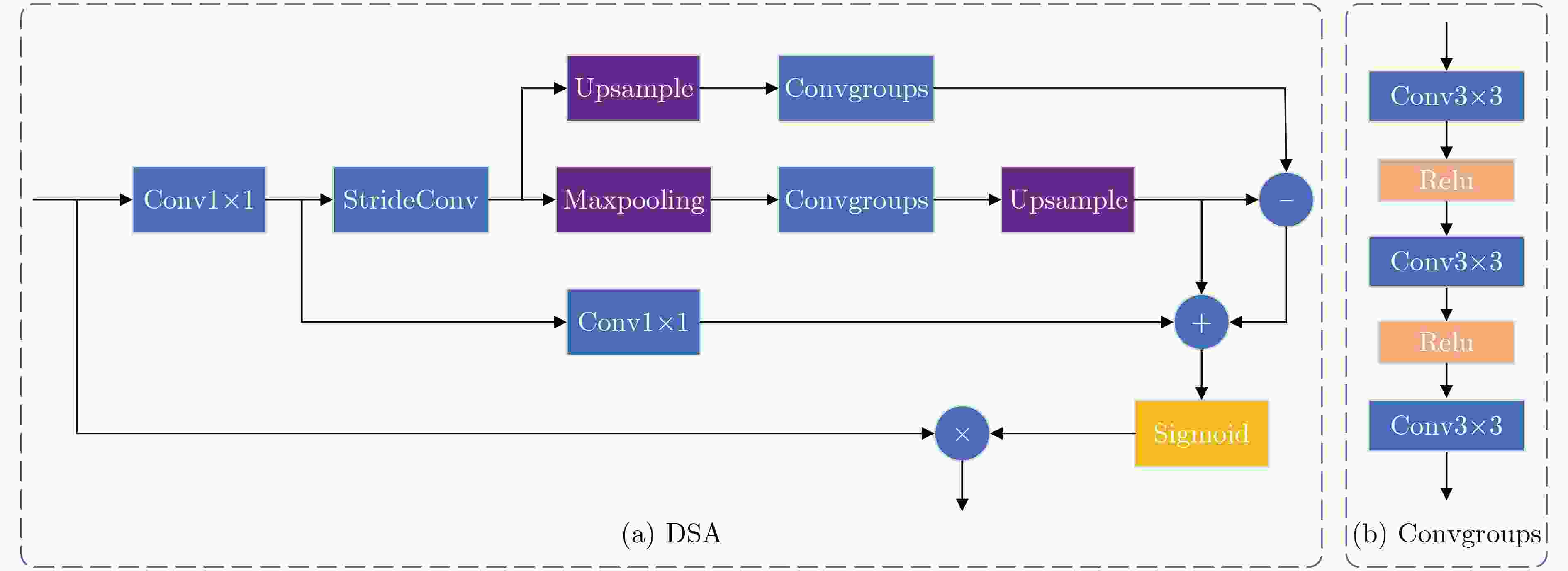
摘要: 传统深层神经网络通常以跳跃连接等方式堆叠深层特征,这种方式容易造成信息冗余。为了提高深层特征信息的利用率,该文提出一种深层特征差异性网络(DFDN),并将其应用于单幅图像超分辨率重建。首先,提出相互投影融合模块(MPFB)提取多尺度深层特征差异性信息并融合,以减少网络传输中上下文信息的损失。第二,提出了差异性特征注意力机制,在扩大网络感受野的同时进一步学习深层特征的差异。第三,以递归的形式连接各模块,增加网络的深度,实现特征复用。将DIV2K数据集作为训练数据集,用4个超分辨率基准数据集对预训练的模型进行测试,并通过与流行算法比较重建的图像获得结果。广泛的实验表明,与现有算法相比,所提算法可以学习到更丰富的纹理信息,并且在主观视觉效果和量化评价指标上都取得最好的排名,再次证明了其鲁棒性和优越性。Abstract: Traditional deep neural networks usually stack deep features in a way such as skip connection, which is easy to cause information redundancy. To improve the utilization of deep feature information, a Deep Feature Differentiation Network (DFDN) is proposed and applied to single image super-resolution. First, multi-scale deep feature differentiation information is extracted and fused by Mutual-Projected Fusion Block (MPFB) to reduce the contextual information loss. Second, a differential feature attention module is proposed to further learn the differences of deep features while expanding the perception field. Third, the modules are connected in a recursive form to increase the network depth and realize feature reuse. The DIV2K dataset is used as the training dataset, and the pre-trained model is tested with four benchmark datasets, and the results are obtained by comparing the reconstructed images with popular algorithms. Extensive experiments show that the algorithm proposed in this study learns richer texture information than existing algorithms and achieves the best rankings in both subjective visualization and quantitative evaluation metrics, which again proves its robustness and superiority.
-
Key words:
- Super resolution /
- Deep feature /
- Feature fusion /
- Convolution neural network /
- Differentiation
-
表 1 MPFB模块和DSA模块对模型性能的影响
算法1 算法2 算法3 算法4 MPFB × × √ √ DSA × √ × √ PSNR
(dB)32.13 32.24 32.27 32.30 SSIM 0.9287 0.9296 0.9300 0.9301 注:加粗字体为每行最优值。 表 2 缩放因子为2、3、4时在基准数据集下的指标对比
模型 缩放因子 Set5[29] Set14[30] BSD100[31] Urban100[24] PSNR(dB) SSIM PSNR(dB) SSIM PSNR(dB) SSIM PSNR(dB) SSIM SRCNN[11] X2 36.66 0.9542 32.43 0.9063 31.36 0.8879 29.50 0.8946 VDSR[25] X2 37.54 0.9587 33.03 0.9124 31.90 0.8960 30.76 0.9140 CARN[26] X2 37.76 0.9590 33.52 0.9166 32.09 0.8978 31.92 0.9256 MSRN[14] X2 38.08 0.9605 33.74 0.9170 32.23 0.9013 32.22 0.9326 IMDN[15] X2 38.00 0.9605 33.63 0.9177 32.19 0.8996 32.17 0.9283 OISR-RK2[17] X2 38.12 0.9609 33.80 0.9193 32.26 0.9006 32.48 0.9317 LatticeNet[27] X2 38.15 0.9610 33.78 0.9193 32.25 0.9005 32.43 0.9302 SwinIR-light[28] X2 38.14 0.9611 33.86 0.9206 32.31 0.9012 32.76 0.9340 DID-D5[18] X2 38.15 0.9610 33.77 0.9190 32.27 0.9006 32.38 0.9305 LBNet[19] X2 — — — — — — — — NGswin[20] X2 38.05 0.9610 33.79 0.9199 32.27 0.9008 32.53 0.9324 DFDN(本文) X2 38.19 0.9612 33.85 0.9199 32.3 0.9013 32.68 0.9335 SRCNN[11] X3 32.75 0.9090 29.30 0.8215 28.41 0.7863 26.24 0.7989 VDSR[25] X3 33.66 0.9213 29.77 0.8314 28.82 0.7976 27.14 0.8279 CARN[26] X3 34.29 0.9255 30.29 0.8407 29.06 0.8034 28.06 0.8493 MSRN[14] X3 34.38 0.9262 30.34 0.8395 29.08 0.8041 28.08 0.8554 IMDN[15] X3 34.36 0.9270 30.32 0.8417 29.09 0.8046 28.17 0.8519 OISR-RK2[17] X3 34.55 0.9282 30.46 0.8443 29.18 0.8075 28.50 0.8597 LatticeNet[27] X3 34.53 0.9281 30.39 0.8424 29.15 0.8059 28.33 0.8538 SwinIR-light[28] X3 34.62 0.9289 30.54 0.8463 29.20 0.8082 28.66 0.8624 DID-D5[18] X3 34.55 0.9280 30.49 0.8446 29.19 0.8069 28.39 0.8566 LBNet[19] X3 34.47 0.9277 30.38 0.8417 29.13 0.8061 28.42 0.8599 NGswin [20] X3 34.52 0.9282 30.53 0.8456 29.19 0.8078 28.52 0.8603 DFDN(本文) X3 34.69 0.9293 30.55 0.8464 29.25 0.8089 28.70 0.8630 SRCNN[11] X4 30.48 0.8628 27.49 0.7503 26.90 0.7101 24.53 0.7221 VDSR[25] X4 31.35 0.8830 28.01 0.7680 27.29 0.7251 25.18 0.7543 CARN[26] X4 32.13 0.8937 28.60 0.7806 27.58 0.7349 26.07 0.7837 MSRN[14] X4 32.07 0.8903 28.60 0.7751 27.52 0.7273 26.04 0.7896 IMDN[15] X4 32.21 0.8948 28.58 0.7811 27.56 0.7353 26.04 0.7838 OISR-RK2[17] X4 32.32 0.8965 28.72 0.7843 27.66 0.7390 26.37 0.7953 LatticeNet[27] X4 32.30 0.8962 28.68 0.7830 27.62 0.7367 26.25 0.7873 SwinIR-light[28] X4 32.44 0.8976 28.77 0.7858 27.69 0.7406 26.47 0.7980 DID-D5[18] X4 32.33 0.8968 28.75 0.7852 27.68 0.7386 26.36 0.7933 LBNet[19] X4 32.29 0.8960 28.68 0.7832 27.62 0.7382 26.27 0.7906 NGswin [20] X4 32.33 0.8963 28.78 0.7859 27.66 0.7396 26.45 0.7963 DFDN(本文) X4 32.56 0.8989 28.87 0.7880 27.73 0.7414 26.59 0.8008 注:黑色加粗字体为每列最优值,蓝色加粗字体为每列次优值 表 3 不同MPFB数量对网络性能的影响
模型 参数量(M) PSNR(dB) SSIM 时间(ms) M=1 1.96 32.29 0.9300 131 M=2 (本文) 3.56 32.53 0.9328 173 M=3 5.17 32.68 0.9338 268 注:加粗字体为每列最优值。 表 4 不同注意力模块对网络性能的影响
模型 ESA DSA Set5 PSNR/SSIM 38.11/0.9611 38.16/0.9612 Set14 PSNR/SSIM 33.60/0.9193 33.61/0.9191 BSD100 PSNR/SSIM 32.27/0.9010 32.31/0.9011 Urban100 PSNR/SSIM 32.39/0.9313 32.53/0.9328 注:加粗字体为每行最优值。 表 5 通道数对网络性能的影响
模型 参数量(M) PSNR(dB) SSIM 时间(ms) C16C16C16 0.80 37.73 0.9599 104 C16C32C64
(本文)3.56 37.97 0.9607 173 C32C32C32 1.95 37.90 0.9604 143 C32C32C64 3.80 37.98 0.9607 184 C64C64C64 6.55 38.04 0.9669 232 注:加粗字体为每列最优值。 表 6 不同残差块数量对网络性能的影响
参数量(M) PSNR(dB) SSIM 时间(ms) Res=2 2.40 37.91 0.9604 150 Res=4
(本文)3.56 37.97 0.9607 173 Res=6 4.73 38.01 0.9608 216 注:加粗字体为每列最优值。 表 7 不同RFFB数量对网络性能的影响
参数量(M) PSNR(dB) SSIM 时间(ms) D=2 1.39 26.08 0.7858 113 D=3
(本文)2.00 26.24 0.7903 153 D=4 2.62 26.34 0.7941 207 注:加粗字体为每列最优值。 -
[1] 陈嘉琪, 刘祥梅, 李宁, 等. 一种超分辨SAR图像水域分割算法及其应用[J]. 电子与信息学报, 2021, 43(3): 700–707. doi: 10.11999/JEIT200366.CHEN Jiaqi, LIU Xiangmei, LI Ning, et al. A high-precision water segmentation algorithm for SAR image and its application[J]. Journal of Electronics & Information Technology, 2021, 43(3): 700–707. doi: 10.11999/JEIT200366. [2] 陈书贞, 曹世鹏, 崔美玥, 等. 基于深度多级小波变换的图像盲去模糊算法[J]. 电子与信息学报, 2021, 43(1): 154–161. doi: 10.11999/JEIT190947.CHEN Shuzhen, CAO Shipeng, CUI Meiyue, et al. Image blind deblurring algorithm based on deep multi-level wavelet transform[J]. Journal of Electronics & Information Technology, 2021, 43(1): 154–161. doi: 10.11999/JEIT190947. [3] 何鹏浩, 余映, 徐超越. 基于动态金字塔和子空间注意力的图像超分辨率重建网络[J]. 计算机科学, 2022, 49(S2): 210900202. doi: 10.11896/jsjkx.210900202.HE Penghao, YU Ying, and XU Chaoyue. Image super-resolution reconstruction network based on dynamic pyramid and subspace attention[J]. Computer Science, 2022, 49(S2): 210900202. doi: 10.11896/jsjkx.210900202. [4] 马子杰, 赵玺竣, 任国强, 等. 群稀疏高斯洛伦兹混合先验超分辨率重建[J]. 光电工程, 2021, 48(11): 210299. doi: 10.12086/oee.2021.210299.MA Zijie, ZHAO Xijun, REN Guoqiang, et al. Gauss-Lorenz hybrid prior super resolution reconstruction with mixed sparse representation[J]. Opto-Electronic Engineering, 2021, 48(11): 210299. doi: 10.12086/oee.2021.210299. [5] 黄友文, 唐欣, 周斌. 结合双注意力和结构相似度量的图像超分辨率重建网络[J]. 液晶与显示, 2022, 37(3): 367–375. doi: 10.37188/CJLCD.2021-0178.HUANG Youwen, TANG Xin, and ZHOU Bin. Image super-resolution reconstruction network with dual attention and structural similarity measure[J]. Chinese Journal of Liquid Crystals and Displays, 2022, 37(3): 367–375. doi: 10.37188/CJLCD.2021-0178. [6] OOI Y K and IBRAHIM H. Deep learning algorithms for single image super-resolution: A systematic review[J]. Electronics, 2021, 10(7): 867. doi: 10.3390/ELECTRONICS10070867. [7] CHEN Hanting, WANG Yunhe, GUO Tianyu, et al. Pre-trained image processing transformer[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 12294–12305. doi: 10.1109/CVPR46437.2021.01212. [8] WANG Xuan, YI Jinglei, GUO Jian, et al. A review of image super-resolution approaches based on deep learning and applications in remote sensing[J]. Remote Sensing, 2022, 14(21): 5423. doi: 10.3390/RS14215423. [9] YANG Jianchao, WRIGHT J, HUANG T, et al. Image super-resolution as sparse representation of raw image patches[C]. 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, USA, 2008: 1–8. doi: 10.1109/CVPR.2008.4587647. [10] 程德强, 陈亮亮, 蔡迎春, 等. 边缘融合的多字典超分辨率图像重建算法[J]. 煤炭学报, 2018, 43(7): 2084–2090. doi: 10.13225/j.cnki.jccs.2017.1263.CHENG Deqiang, CHEN Liangliang, CAI Yingchun, et al. Image super-resolution reconstruction based on multi-dictionary and edge fusion[J]. Journal of China Coal Society, 2018, 43(7): 2084–2090. doi: 10.13225/j.cnki.jccs.2017.1263. [11] DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281. [12] SHI Wenzhe, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1874–1883. doi: 10.1109/CVPR.2016.207. [13] LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, USA, 2017: 1132–1140. doi: 10.1109/CVPRW.2017.151. [14] LI Juncheng, FANG Faming, MEI Kangfu, et al. Multi-scale residual network for image super-resolution[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 527–542. doi: 10.1007/978-3-030-01237-3_32. [15] HUI Zheng, GAO Xinbo, YANG Yunchu, et al. Lightweight image super-resolution with information multi-distillation network[C]. The 27th ACM International Conference on Multimedia, Nice, France, 2019: 2024–2032. doi: 10.1145/3343031.3351084. [16] 程德强, 郭昕, 陈亮亮, 等. 多通道递归残差网络的图像超分辨率重建[J]. 中国图象图形学报, 2021, 26(3): 605–618. doi: 10.11834/jig.200108.CHENG Deqiang, GUO Xin, CHEN Liangliang, et al. Image super-resolution reconstruction from multi-channel recursive residual network[J]. Journal of Image and Graphics, 2021, 26(3): 605–618. doi: 10.11834/jig.200108. [17] HE Xiangyu, MO Zitao, WANG Peisong, et al. ODE-inspired network design for single image super-resolution[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 1732–1741. doi: 10.1109/CVPR.2019.00183. [18] LI Longxi, FENG Hesen, ZHENG Bing, et al. DID: A nested dense in dense structure with variable local dense blocks for super-resolution image reconstruction[C]. 2020 25th International Conference on Pattern Recognition, Milan, Italy, 2021: 2582–2589. doi: 10.1109/ICPR48806.2021.9413036. [19] GAO Guangwei, WANG Zhengxue, LI Juncheng, et al. Lightweight bimodal network for single-image super-resolution via symmetric CNN and recursive transformer[C]. The Thirty-First International Joint Conference on Artificial Intelligence, Vienna, Austria, 2022: 913–919. doi: 10.24963/ijcai.2022/128. [20] CHOI H, LEE J, and YANG J. N-gram in Swin transformers for efficient lightweight image super-resolution[C]. The IEEE/CVF Computer Society Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 2071–2081. doi: 10.1109/CVPR52729.2023.00206. [21] HARIS M, SHAKHNAROVICH G, and UKITA N. Deep back-projection networks for super-resolution[C]. The 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 1664–1673. doi: 10.1109/CVPR.2018.00179. [22] LIU Jie, ZHANG Wenjie, TANG Yuting, et al. Residual feature aggregation network for image super-resolution[C]. The IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 2356–2365. doi: 10.1109/CVPR42600.2020.00243. [23] DAI Tao, CAI Jianeui, ZHANG Yongbing, et al. Second-order attention network for single image super-resolution[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 11057–11066. doi: 10.1109/CVPR.2019.01132. [24] HUANG Jiabin, SINGH A, and AHUJA N. Single image super-resolution from transformed self-exemplars[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 5197–5206. doi: 10.1109/CVPR.2015.7299156. [25] KIM J, LEE J K, and LEE K M. 2016. Accurate image super-resolution using very deep convolutional networks[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 1646–1654. doi: 10.1109/CVPR.2016.182. [26] AHN N, KANG B, and SOHN K A. Fast, accurate, and lightweight super-resolution with cascading residual network[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 256–272. doi: 10.1007/978-3-030-01249-6_16. [27] LUO Xiaotong, XIE Yuan, ZHANG Yulun, et al. LatticeNet: Towards lightweight image super-resolution with lattice block[C]. The 16th European Conference on Computer Vision, Glasgow, UK, 2020: 272–289. doi: 10.1007/978-3-030-58542-6_17. [28] LIANG Jingyun, CAO Jiezhang, SUN Guolei, et al. SwinIR: Image restoration using swin transformer[C]. The IEEE/CVF International Conference on Computer Vision Workshops, Montreal, Canada, 2021: 1833–1844. doi: 10.1109/ICCVW54120.2021.00210. [29] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]. British Machine Vision Conference, Surrey, UK, 2012: 1–10. [30] ZEYDE R, ELAD M, and PROTTER M. On single image scale-up using sparse-representations[C]. The 7th International Conference on Curves and Surfaces, Avignon, France, 2010: 711–730. doi: 10.1007/978-3-642-27413-8_47. [31] MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]. Proceedings Eighth IEEE International Conference on Computer Vision, Vancouver, Canada, 2001: 416–423. doi: 10.1109/ICCV.2001.937655. -





 下载:
下载:







 下载:
下载:
