基于任务感知关系网络的少样本图像分类

郭礼华; 王广飞

doi:10.11999/JEIT230162

基于任务感知关系网络的少样本图像分类

doi: 10.11999/JEIT230162

郭礼华^,,
王广飞

华南理工大学电子与信息学院广州 510641

基金项目: 广东省基础与应用基础研究基金(2022A1515011549, 2023A1515011104)

详细信息

作者简介:
郭礼华：男，副教授，研究方向为图像识别、机器学习和图像质量评价

王广飞：男，硕士生，研究方向为少样本图像分类

通讯作者:
郭礼华　guolihua@scut.edu.cn

11 https://plato.stanford.edu/entries/perceptual-learning/
中图分类号: TN911.73; TP391.41
计量
- 文章访问数: 520
- HTML全文浏览量: 383
- PDF下载量: 83
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-16
- 修回日期: 2023-08-17
- 网络出版日期: 2023-08-21
- 刊出日期: 2024-03-27

Few-shot Image Classification Based on Task-Aware Relation Network

GUO Lihua^,,
WANG Guangfei

School of Electronic and Information, South China University of Technology, Guangzhou 510641, China

Funds: Guangdong Basic and Applied Basic Research Foundation (2022A1515011549, 2023A1515011104)

摘要

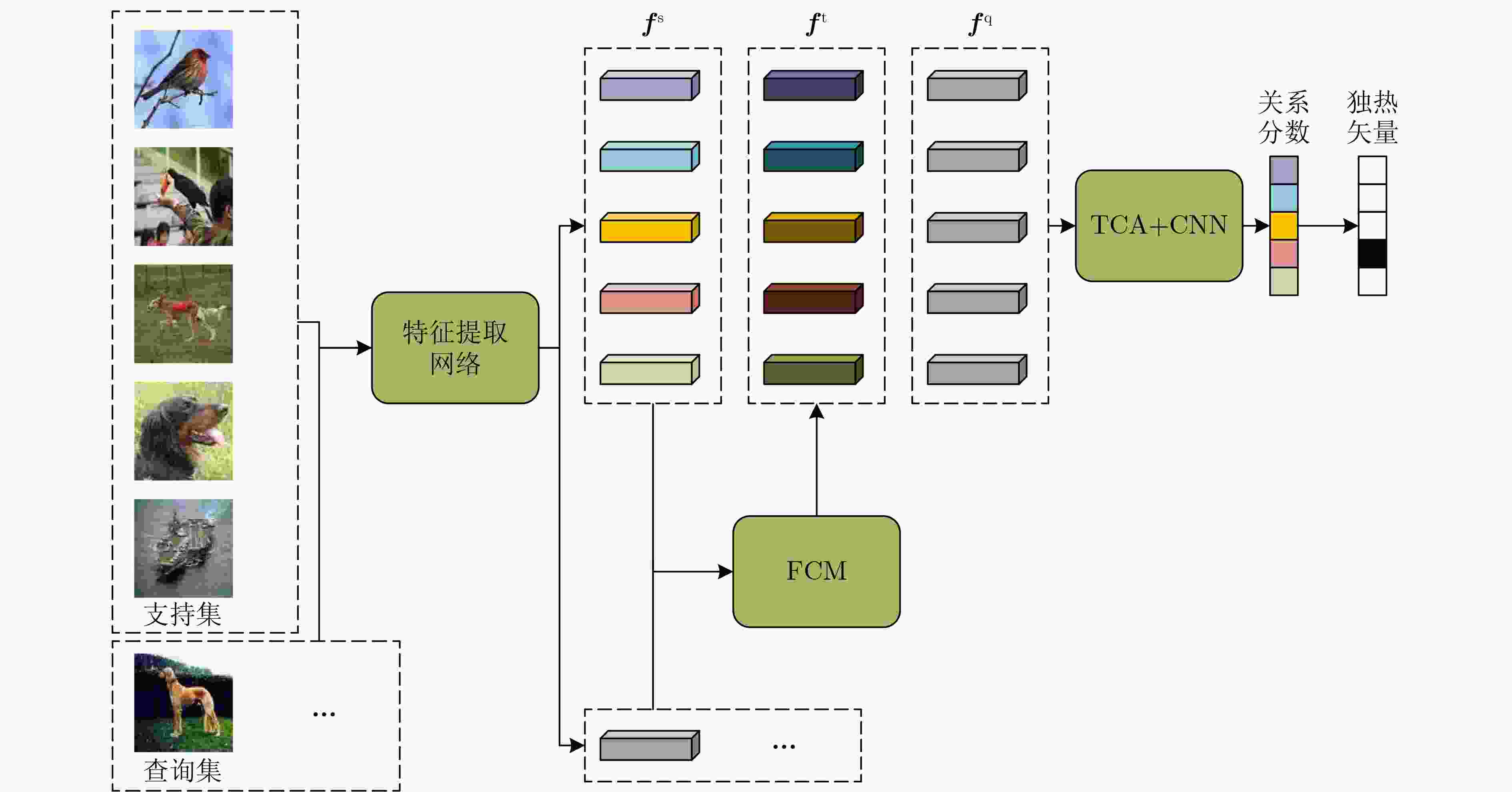
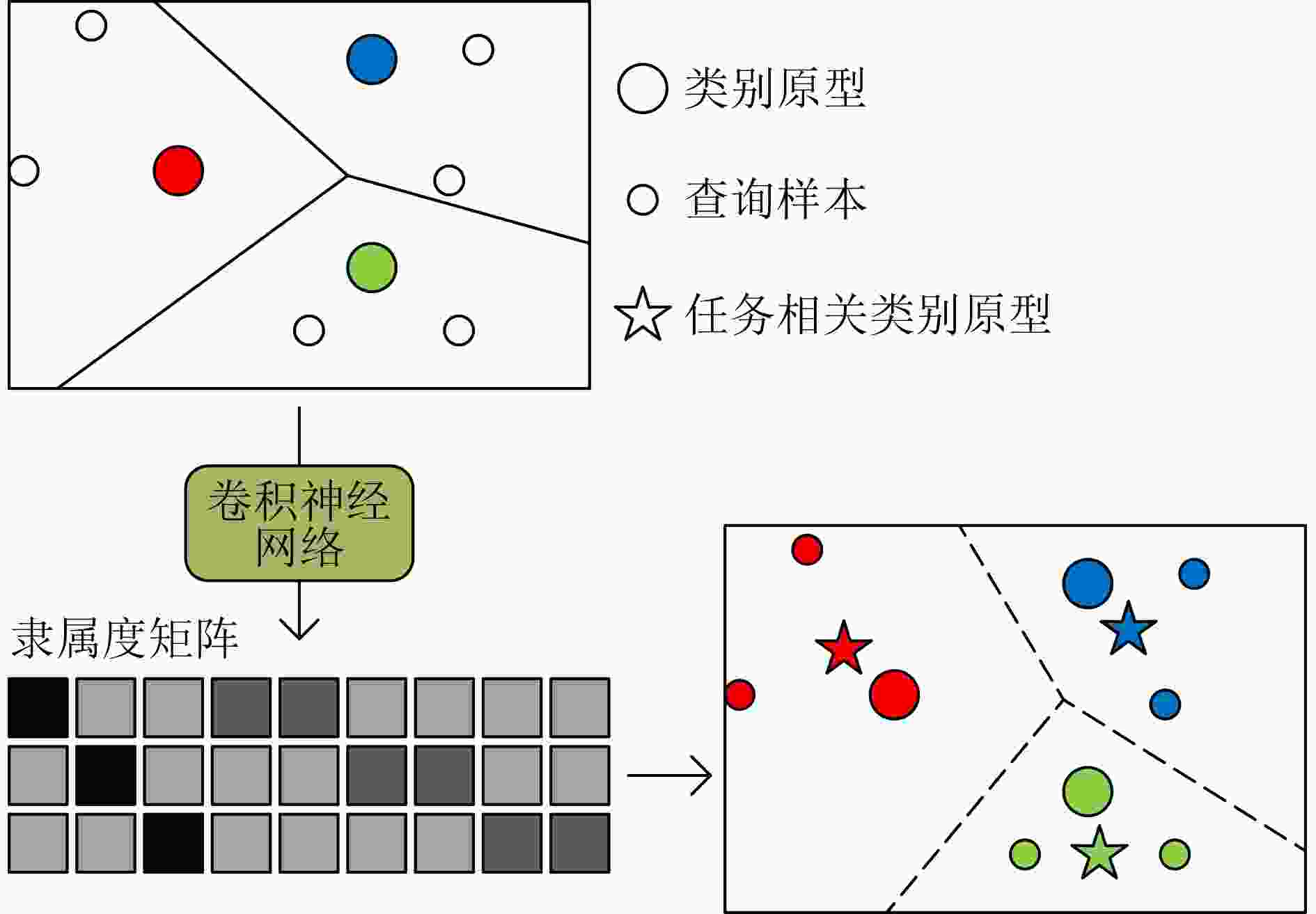
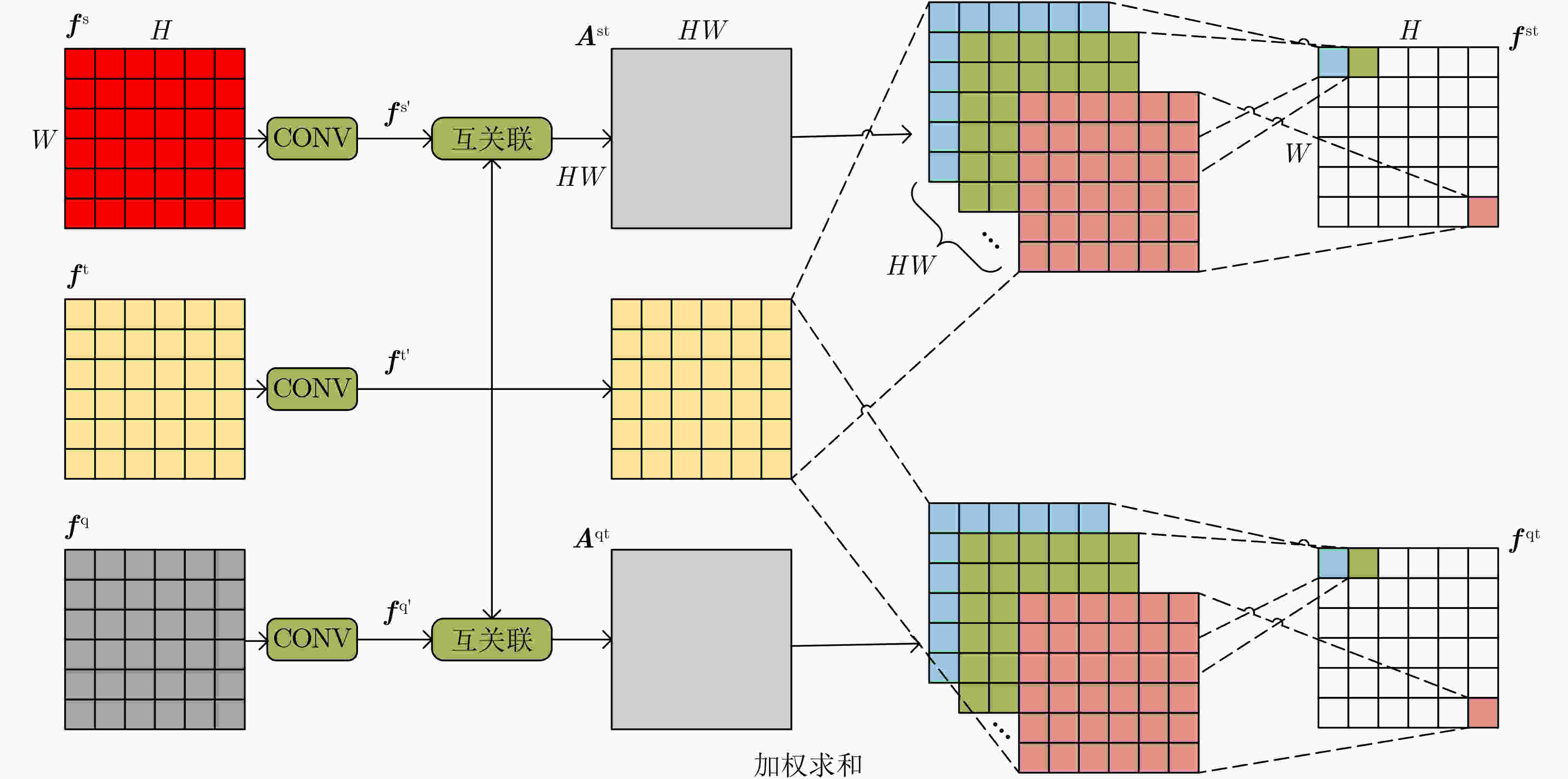
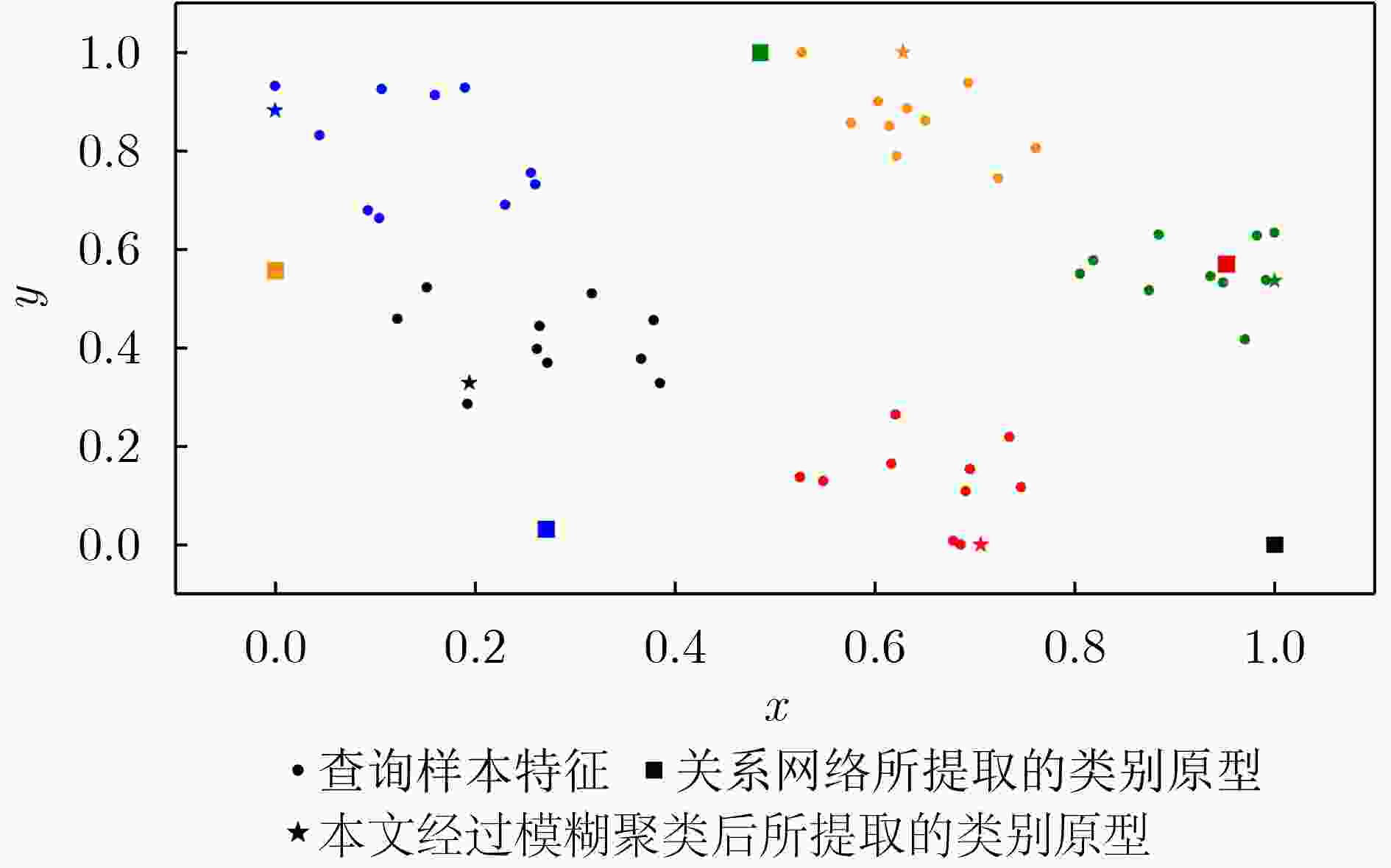
摘要: 针对关系网络(RN)模型缺乏对分类任务整体相关信息的感知能力的问题，该文提出基于任务感知关系网络(TARN)的小样本学习(FSL)算法。引入模糊C均值(FCM)聚类生成基于任务全局分布的类别原型，同时设计任务相关注意力机制(TCA)，改进RN中的1对1度量方式，使得在与类别原型对比时，局部特征聚合了任务全局信息。和RN比，在数据集Mini-ImageNet上，5-way 1-shot和5-way 5-shot设置中的分类准确率分别提高了8.15%和7.0%，在数据集Tiered-ImageNet上，5-way 1-shot和5-way 5-shot设置中的分类准确率分别提高了7.81%和6.7%。与位置感知的关系网络模型比，在数据集Mini-ImageNet上，5-way 1-shot设置中分类准确率也提高了1.24%。与其他小样本图像分类算法性能比较，TARN模型在两个数据集上都获得了最佳的识别精度。该方法将任务相关信息和度量网络模型进行结合可以有效提高小样本图像分类准确率。
- 小样本学习 /
- 图像分类 /
- 度量学习 /
- 任务感知 /
- 关系网络
Abstract: Considering that Relation Network (RN) ignores the global task correlation information, a Few-Shot Learning(FSL)method based on a Task-Aware Relation Network (TARN) for fully using global task correlation information is proposed in this paper. Method class prototype based on global task relationship is created using the Fuzzy C-Mean (FCM) clustering algorithm, and a Task Correlation Attention mechanism (TCA) is designed to improve the one-vs-one evaluation metric in RN for fusing the global task relationship into features. Compared with RN, in the Mini-ImageNet dataset, the classification accuracy of 5-way 1-shot and 5-way 5-shot settings is increased by 8.15% and 7.0% respectively. While in the Tiered-ImageNet dataset, the classification accuracy of 5-way 1-shot and 5-way 5-shot settings is increased by 7.81 and 6.7% respectively. Compared with the position-awareness relation network, in Mini-ImageNet, the classification accuracy of 5-way 1-shot settings is still increased by 1.24%. Compared with other few-shot image classification methods, TARN also achieves the best performance in these two datasets. The combination of the relation network and task correlation can effectively improve the few-shot image classification accuracy.
- Few-Shot Learning (FSL) /
- Image classification /
- Metric learning /
- Task-aware /
- Relation Network(RN)

HTML全文

图 1 TARN模型整体框架

下载: 全尺寸图片幻灯片

图 2 FCM模块计算任务相关类别原型的示意图

下载: 全尺寸图片幻灯片

图 3 TCA算法流程

下载: 全尺寸图片幻灯片

图 4 TARN与RN, PARN的对照Grad-CAM热力图

下载: 全尺寸图片幻灯片

图 5 5-way 1-shot模式下，查询样本和类别原型经过t-SNE降维后可视化图

下载: 全尺寸图片幻灯片

表 1 Mini-ImageNet数据集上小样本分类准确率(%)

模型	特征提取网络	5-way 1-shot	5-way 5-shot
Reptile	Conv4	49.97	65.99
RN		50.44	65.32
BOIL		49.61	66.45
SNAL		55.71	68.88
OVE		50.02	64.58
FEAT		55.15	71.61
PARN		55.22	71.55
TARN(本文)		56.46	71.77
FEAT	ResNet12	62.96	78.49
RN		56.67	73.73
TADAM		58.50	76.70
DSN		64.60	79.51
NCA		62.55	78.27
Meta-Baseline		63.17	79.26
PSST		64.05	80.24
P-Transfer		64.21	80.38
TARN(本文)		64.82	80.73

下载: 导出CSV

表 2 Tiered-ImageNet数据集上小样本分类准确率(%)

模型	特征提取网络	5-way1-shot	5-way 5-shot
ProtoNets	Conv4	53.31	72.69
RN		53.18	69.65
BOIL		49.35	69.37
MELR		56.3	73.22
TARN(本文)		57.95	74.68
FEAT	ResNet12	70.80	84.79
DSN		66.22	82.79
RN		66.18	80.15
Meta-Baseline		68.62	83.74
NCA		68.35	83.20
UniSiam		67.01	84.47
MCL		72.01	86.02
BaseTransformer		72.46	84.96
MELR		72.14	87.01
TARN(本文)		73.99	86.85

下载: 导出CSV

表 3 3种模型的训练时间和测试时间对比

模型	特征提取网络	训练时间(min)	测试时间(ms)
RN	Conv4	215.2	44.95
PARN		250.2	63.57
TARN		251.1	63.93
RN	ResNet12	485.8	150.85
PARN		857.9	280.57
TARN		861.3	281.71

下载: 导出CSV

表 4 Mini-ImageNet数据集的消融实验(%)

RN	HCM	FCM	TCA	5-way 1-shot	5-way 5-shot
√				51.21	65.97
√	√			52.39	67.12
√		√		54.00	67.90
√	√		√	55.22	70.62
√		√	√	56.46	71.77

下载: 导出CSV

参考文献(21)

[1]	SUNG F, YANG Fongxin, ZHANG Li, et al. Learning to compare: Relation network for few-shot learning[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 1199–1208.
[2]	WU Ziyang, LI Yuwei, GUO Lihua, et al. PARN: Position-aware relation networks for few-shot learning[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea (South), 2019: 6658–6666.
[3]	ORESHKIN B N, RODRIGUEZ P, and LACOSTE A. TADAM: Task dependent adaptive metric for improved few-shot learning[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 719–729.
[4]	MANIPARAMBIL M, MCGUINNESS K, and O'CONNOR N E. BaseTransformers: Attention over base data-points for One Shot Learning[C]. The 33rd British Machine Vision Conference, London, UK, 2022: 482. doi: arxiv-2210.02476.
[5]	LIU Yang, ZHANG Weifeng, XIANG Chao, et al. Learning to affiliate: Mutual centralized learning for few-shot classification[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 14391–14400.
[6]	FINN C, ABBEEL P, and LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[C]. The 34th International Conference on Machine Learning, Sydney, Australia, 2017: 1126–1135. doi: 10.5555/3305381.3305498.
[7]	NICHOL A, ACHIAM J, and SCHULMAN J. On first-order meta-learning algorithms[EB/OL]. https://arxiv.org/abs/1803.02999, 2018.
[8]	OH J, YOO H, KIM C, et al. BOIL: Towards representation change for few-shot learning[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–24.doi: 10.48550/arXiv.2008.08882.
[9]	CHEN Yinbo, LIU Zhuang, XU Huijuan, et al. Meta-baseline: Exploring simple meta-learning for few-shot learning[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 9042–9051. doi: 10.1109/ICCV48922.2021.00893.
[10]	SHEN Zhiqiang, LIU Zechun, QIN Jie, et al. Partial is better than all: Revisiting fine-tuning strategy for few-shot learning[C]. The 35th AAAI Conference on Artificial Intelligence, Palo Alto, USA, 2021: 9594–9602.
[11]	SNELL J and ZEMEL R. Bayesian few-shot classification with one-vs-each pólya-gamma augmented Gaussian processes[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–34. doi: 10.48550/arXiv.2007.10417.
[12]	DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: A large-scale hierarchical image database[C]. 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, USA, 2009: 248–255.
[13]	REN Mengye, TRIANTAFILLOU E, RAVI S, et al. Meta-learning for semi-supervised few-shot classification[EB/OL]. https://arxiv.org/abs/1803.00676, 2018.
[14]	MISHRA N, ROHANINEJAD M, CHEN Xi, et al. A simple neural attentive meta-learner[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018: 1–17. doi: 10.48550/arXiv.1707.03141.
[15]	YE Hanjia, HU Hexiang, ZHAN Dechuan, et al. Few-shot learning via embedding adaptation with set-to-set functions[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 8805–8814.
[16]	FEI Nanyi, LU Zhiwu, XIANG Tao, et al. MELR: Meta-learning via modeling episode-level relationships for few-shot learning[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–20.
[17]	SIMON C, KONIUSZ P, NOCK R, et al. Adaptive subspaces for few-shot learning[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 4135–4144.
[18]	LAENEN S and BERTINETTO L. On episodes, prototypical networks, and few-shot learning[C]. The 35th International Conference on Neural Information Processing Systems, 2021: 24581–24592. doi: 10.48550/arXiv.2012.09831.
[19]	LU Yuning, WEN Liangjian, LIU Jianzhuang, et al. Self-supervision can be a good few-shot learner[C]. The 17th European Conference on Computer Vision, Tel Aviv, Israel, 2022: 740–758.
[20]	CHEN Zhengyu, GE Jixie, ZHAN Heshen, et al. Pareto self-supervised training for few-shot learning[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 13658–13667.
[21]	SELVARAJU R R, COGSWELL M, DAS A, et al. Grad-CAM: Visual explanations from deep networks via gradient-based localization[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 618–626.