Jamming Pattern Open Set Recognition Based on Hyperspherical Triplet Coding
-
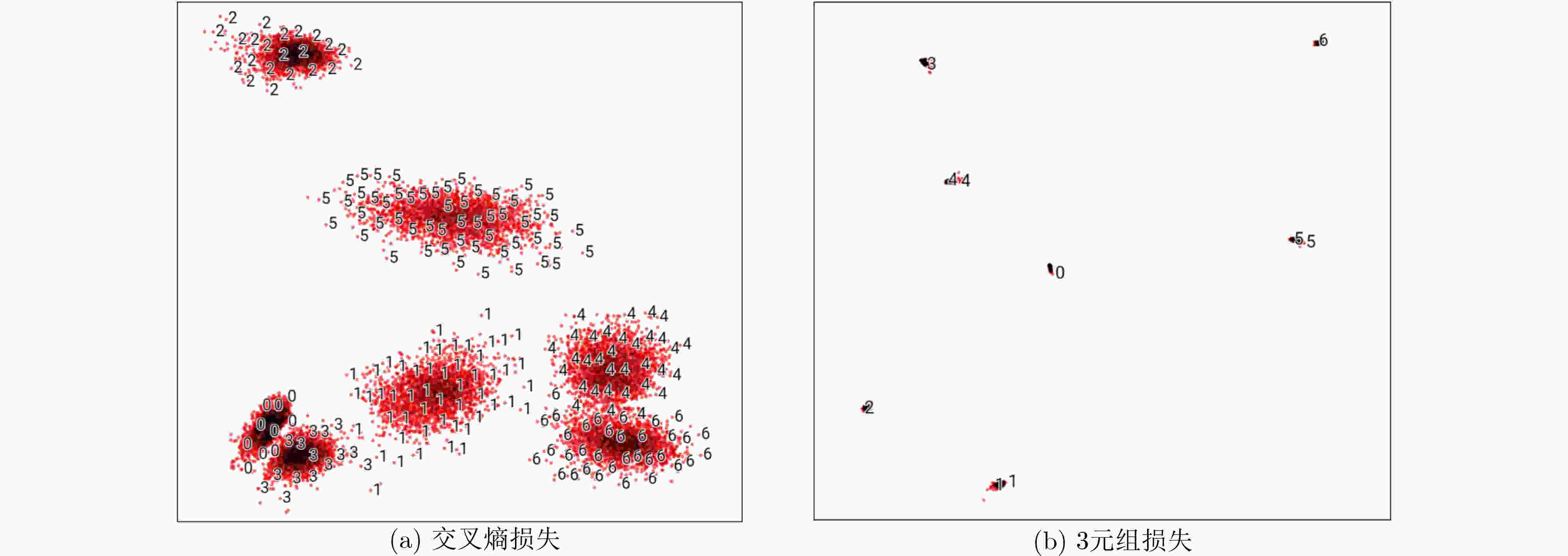
摘要: 干扰模式识别是现代军事通信对抗中必不可少的一环,随着复杂电磁环境当中各种新型恶意干扰样式层出不穷,对于未知型干扰的判决也变得愈发重要。因此,要求干扰模式识别算法保持对于已知型干扰高精度识别的同时,也能够完成对于未知型干扰的判决,以排除未知型恶意干扰的影响。基于此,该文将未知型干扰存在时的干扰模式识别问题建模为开集识别问题,并提出一种基于超球面3元组编码的干扰模式开集识别方法。所提方法基于超球面3元组对输入的时频图像进行降维编码以提高识别精度,然后采用元识别分类器准确地完成干扰模式开集识别任务。通过仿真试验证明该算法在干信比大于–2 dB时能够高效地完成开放空间中的干扰模式识别任务。Abstract: Jamming pattern recognition is an indispensable part of modern military communication countermeasure. With the emergence of various new malicious jamming patterns in complex electromagnetic environment, the judgment of unknown jamming has become more and more important. Therefore, the jamming pattern recognition algorithm is required to maintain the high-precision recognition of the known jamming, and can also complete the judgment of the unknown jamming to eliminate the influence of the unknown malicious jamming. Based on this, the jamming pattern recognition problem in the presence of unknown jamming as an open set recognition problem is modeled in this paper, and a jamming pattern open set recognition method based on hyperspherical triple coding is proposed. The proposed method uses hyperspherical triples to reduce the dimension of the input time-frequency image to improve the recognition accuracy, and then uses the meta-recognition classifier to accurately complete the open set recognition of the jamming pattern. The simulation results show that the algorithm can efficiently complete the jamming pattern recognition task in open space when the jamming-to-signal ratio is greater than –2 dB.
-
Key words:
- Unknown interference signal /
- Open set recognition /
- Triplet loss /
- Hypersphere /
- Meta recognition
-
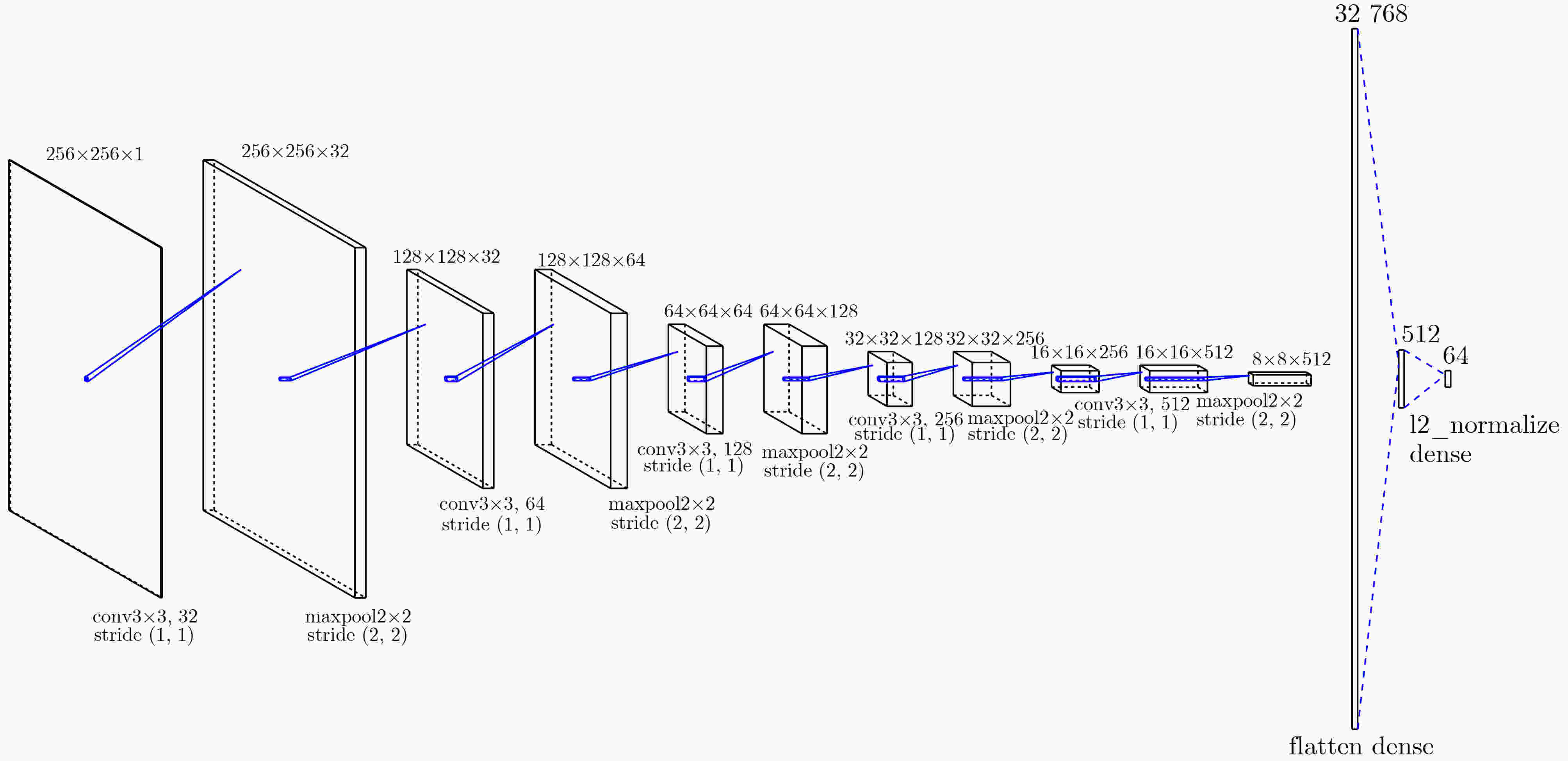
算法1 基于超球面3元组编码的干扰模式开集识别算法 准备通过基于3元组损失训练的编码器后的训练集编码数据集合$ {X^{{\text{train}}}}{\text{:\{ }}{Z_1}{\text{,}}{Z_2}{\text{,}} \cdots {\text{,}}{Z_K}{\text{\} }} $和测试集编码数据集合$ {X^{{\text{test}}}} $,其中
$ {Z_{i \in 1, 2,\cdots ,K}}:\{ {z_1},{z_2}, \cdots ,{z_{{n_i}}}\} $表示训练集第$ i $类已知型干扰样本数据集合且样本数为$ {n_i} $,样本数据为$ {z_j} $,设定阈值相关常数$ C $(通过率)。(1)拟合各已知型干扰Weibull模型; for $ \left\{{Z}_{i}\right\},\;i=1,2,\cdots ,K $ do 根据$ {\text{MA}}{{\text{V}}_i} = {\text{mean}}({Z_i}) $计算质心坐标$ {\text{MA}}{{\text{V}}_i} $; for $ {z_j} \in {Z_i} $ do 选择距离类型并计算$ {z_j} $到质心$ {\text{MA}}{{\text{V}}_i} $的距离$ {d_j} $以构成距离合集$ {D_i}:\{ {d_1},{d_2}, \cdots ,{d_{{n_i}}}\} $; end for $ {D_i} $中的极大值分布按照Weibull分类来拟合,得到第$ i $类的$ {\text{Weibul}}{{\text{l}}_i} $分布模型。 end for (2)各已知型干扰Weibull模型信心分数阈值设置; for $ \left\{i\right\},\;i=1,2,\cdots ,K $ do for $ {z_j} \in {Z_i} $ do 根据$ {\text{Weibul}}{{\text{l}}_i} $模型计算$ {z_j} $的信心分数$ {c_j} = 1 - {\text{Weibul}}{{\text{l}}_i}({d_j}) $以构成信心分数合集$ {C_i}:\{ {c_1},{c_2}, \cdots ,{c_{{n_i}}}\} $; end for 将信心分数集合降序排列得$ {C'_i} :\{ {c'_1},{c'_2}, \cdots ,{c'_{{n_i}}}\} $; 将第$ i $类训练集样本数$ {n_i} $与通过率$ p\% $相乘得通过样本数$ {\text{nu}}{{\text{m}}_i} = {n_i} \times p\% $; 第$ i $类信心分数阈值$ {\xi _i} = {c'_{{\text{nu}}{{\text{m}}_i}}} $,即$ {C'_i} $中第$ {\text{nu}}{{\text{m}}_i} $个数值。 end for (3)测试样本$ {x_t} \in {X^{{\text{test}}}} $开集识别,设置未知型干扰标志$ {\text{flag}} = 0 $; for $ \left\{i\right\},\; i=1,2,\cdots ,K $ do 计算$ {x_t} $到质心$ {\text{MA}}{{\text{V}}_i} $的距离$ {d_{ti}} $; 计算$ {x_t} $属于第$ i $类的信心分数$ {c_{ti}} = 1 - {\text{Weibul}}{{\text{l}}_i}({d_{ti}}) $; if $ {c_{ti}} \gt {\xi _i} $ do 判断类别为第$ i $类已知型干扰信号并设置$ {\text{flag}} = 1 $; Break end if end for if $ {\text{flag}} = 0 $ do 判断类别为未知型干扰信号。 end if 表 1 干扰信号参数设置
干扰样式 干扰参数 JSR 干扰个数 干扰带宽因子 中心频率 初始相位 单音干扰(CW) 无 无 10~20 MHz 0~2π –2:2:10 dB 多音干扰(MTJ) 3~6 无 10~20 MHz 宽带干扰(PBNJ) 干扰带宽因子 0.2~0.8 线性扫频干扰(LFM) 带宽因子 扫频周期 依赖于带宽因子的大小,保证信号
带宽完整地位于感知带宽内。0.2~0.8 0.05~0.25 ms 正弦调频干扰(SFM) 带宽因子 扫频周期 0.2~0.8 0.05~0.25 ms 周期脉冲噪声干扰(PPNJ) 脉冲周期 脉冲周期内占空比 脉冲干扰触发时间 0.05~0.25 ms 0.1~0.5 0~0.5 ms 跳频干扰(FHJ) 驻留时间 跳变频率集 信号带宽 0.1 ms 10.5:1:19.5 MHz 1 MHz 噪声调频干扰(NFM) 调频因子 中心频率 0.7~1.5 10~20 MHz QPSK数字调频干扰 信息速率 信号带宽 中心频率 1 Mbit/s 1 MHz 10~20 MHz 样本数 每种干扰样式在每个JSR下分别生成500个样本,并且每个样本的干扰参数取值均服从
给定参数范围内的均匀分布,其中训练集样本数:测试集样本数=4:1。表 2 干扰模式开集识别试验数据组合
试验数据组合序号 已知型干扰 未知型干扰 组合1 CW MTJ LFM PBNJ PPNJ FHJ SFM NFM QPSK 组合2 CW MTJ LFM PBNJ PPNJ FHJ NFM SFM QSPK 组合3 CW MTJ LFM PBNJ PPNJ FHJ QPSK SFM NFM 组合4 CW MTJ LFM PBNJ PPNJ SFM NFM FHJ QPSK 组合5 CW MTJ LFM PBNJ PPNJ SFM QPSK FHJ NFM 组合6 CW MTJ LFM PBNJ PPNJ NFM QPSK FHJ SFM 表 3 不同分类方法的干扰模式开集识别整体性能对比(%)
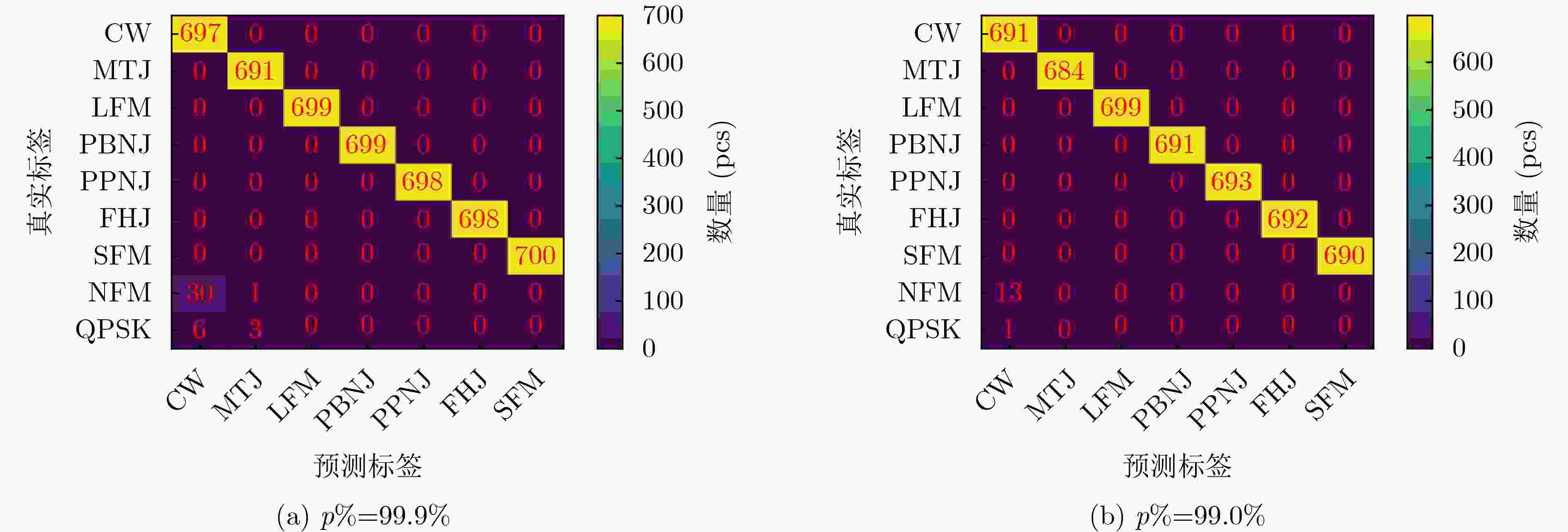
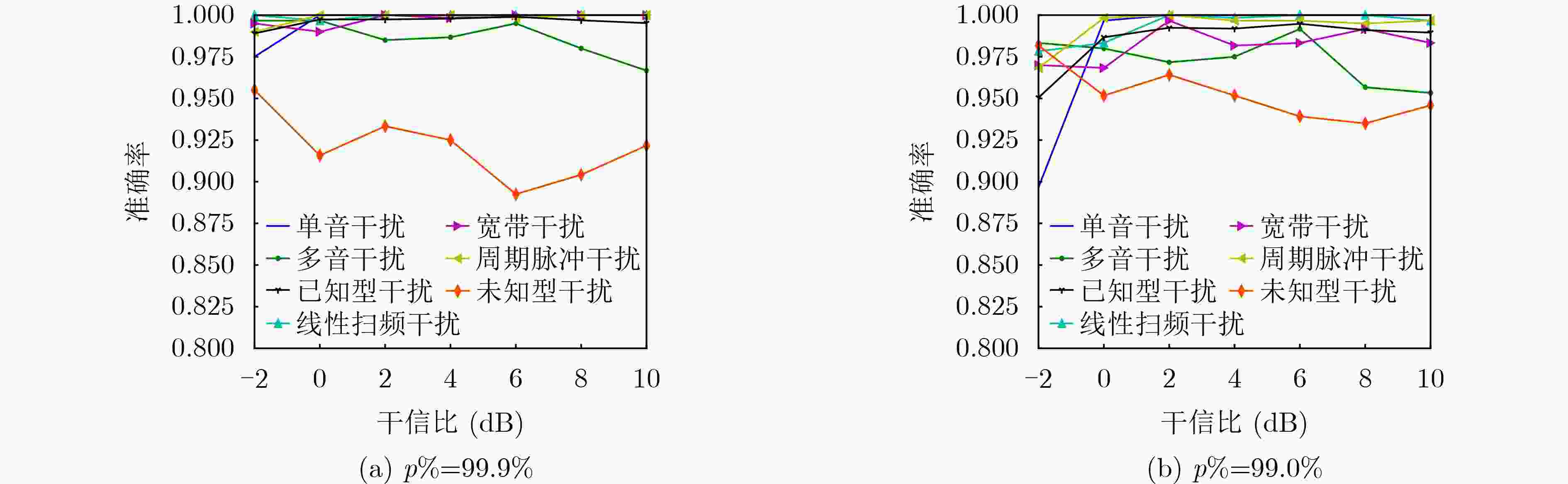
分类方法 TNR TPR(Recall) Precision F1-score SVDD 89.4762 99.0748 97.0876 98.0628 OCSVM 88.4762 98.9932 96.8261 97.8820 余弦距离 80.1191 99.8708 94.6819 97.1910 元识别方法($ p\% = 99.9\% $) 92.1072 99.6123 97.8179 98.6988 表 4 不同干扰模式开集识别算法整体性能对比(%)
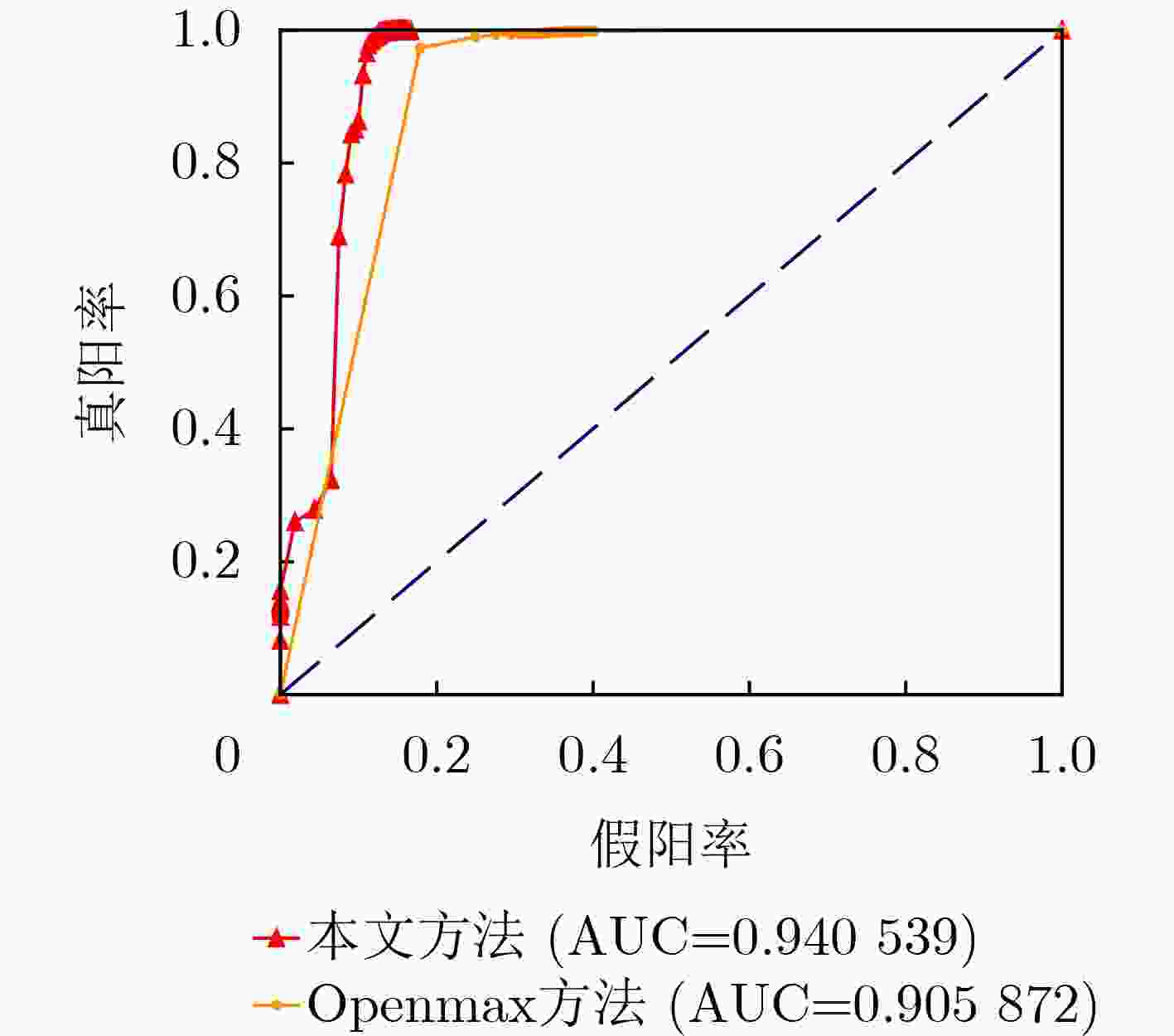
参数 TNR TPR(Recall) Precision F1-score 本文方法($ p\% = 99.9\% $) 92.1072 99.6123 97.8179 98.6988 本文方法($ p\% = 99.0\% $) 95.2738 98.5408 98.6626 98.5982 文献[15]方法 59.5714 99.9184 90.1224 94.6436 openmax方法 84.0238 99.7619 95.7828 97.6917 表 5 已知型干扰与未知型干扰混合情况下该文方法的判决准确率(%)
本文方法 组合1 组合2 组合3 组合4 组合5 组合6 平均值 $ p\% = 99.9\% $ 65.7143 66.5306 66.3265 69.7449 66.3265 58.9796 65.6037 $ p\% = 99.0\% $ 79.9490 77.0918 77.6020 80.5102 75.9184 71.9388 77.1684 -
[1] GONG Shixian, WEI Xizhang, LI Xiang, et al. Mathematic principle of active jamming against wideband LFM radar[J]. Journal of Systems Engineering and Electronics, 2015, 26(1): 50–60. doi: 10.1109/JSEE.2015.00008. [2] SHU Jianfei, LIAO Yanping, and Luan Xiaoming. An interference recognition method based on improved genetic algorithm[C]. The 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 2021: 496–500. doi: 10.1109/ICCC54389.2021.9674374. [3] 周鑫, 何晓新, 郑昌文. 基于图像深度学习的无线电信号识别[J]. 通信学报, 2019, 40(7): 114–125. doi: 10.11959/j.issn.1000- 436x.2019167.ZHOU Xin, HE Xiaoxin, and ZHENG Changwen. Radio signal recognition based on image deep learning[J]. Journal on Communications, 2019, 40(7): 114–125. doi: 10.11959/j.issn.1000-436x.2019167. [4] 徐昊. 卫星宽带跳频系统的干扰检测识别技术研究[D]. [硕士论文], 电子科技大学, 2021. doi: 10.27005/d.cnki.gdzku.2021.000573.XU Hao. Research on jamming detection and recognition technology in satellite broadband frequency hopping systems[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021. doi: 10.27005/d.cnki.gdzku.2021.000573. [5] WANG Pengyu, CHENG Pengyu, DONG Binhong, et al. Bring globality into convolutional neural networks for wireless interference classification[J]. IEEE Wireless Communications Letters, 2022, 11(3): 538–542. doi: 10.1109/LWC.2021.3135901. [6] DONG Yihong, JIANG Xiaohan, ZHOU Huaji, et al. SR2CNN: Zero-Shot learning for signal recognition[J]. IEEE Transactions on Signal Processing, 2021, 69: 2316–2329. doi: 10.1109/TSP.2021.3070186. [7] TANG Yan, ZHAO Zhijin, CHEN Jie, et al. Open world recognition of communication jamming signals[J]. China Communications, 2023, 20(6): 199–214. doi: 10.23919/JCC.2023.00.029. [8] CHEN Xiangwei, ZHAO Zhijin, YE Xueyi, et al. Efficient open-set recognition for interference signals based on convolutional prototype learning[J]. Applied Sciences, 2022, 12(9): 4380. doi: 10.3390/app12094380. [9] GENG Chuanxing, HUANG Shengjun, and CHEN Songcan. Recent advances in open set recognition: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(10): 3614–3631. doi: 10.1109/TPAMI.2020.2981604. [10] RUFF L, GÖRNITZ N, DEECKE L, et al. Deep one-class classification[C]. The 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 4390–4399. [11] SCHEIRER W J, JAIN L P, and BOULT T E. Probability models for open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2317–2324. doi: 10.1109/TPAMI.2014.2321392. [12] BENDALE A and BOULT T E. Towards open set deep networks[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1563–1572. doi: 10.1109/CVPR.2016.173. [13] CHEN Guangyao, PENG Peixi, WANG Xiangqian, et al. Adversarial reciprocal points learning for open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(11): 8065–8081. doi: 10.1109/TPAMI.2021.3106743. [14] KONG Shu and RAMANAN D. OpenGAN: Open-set recognition via open data generation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022. doi: 10.1109/TPAMI.2022.3184052. [15] HAN Hao, LI Wen, FENG Zhibin, et al. Proceed from known to unknown: Jamming pattern recognition under open-set setting[J]. IEEE Wireless Communications Letters, 2022, 11(4): 693–697. doi: 10.1109/LWC.2021.3140145. [16] SCHROFF F, KALENICHENKO D, and PHILBIN J. FaceNet: A unified embedding for face recognition and clustering[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 815–823. doi: 10.1109/CVPR.2015.7298682. [17] 周琳娜, 王东明, 郭云彪, 等. 基于数字图像边缘特性的形态学滤波取证技术[J]. 电子学报, 2008, 36(6): 1047–1051. doi: 10.3321/j.issn:0372-2112.2008.06.002.ZHOU Linna, WANG Dongming, GUO Yunbiao, et al. Exposing digital forgeries by detecting image blurred mathematical morphology edge[J]. Acta Electronica Sinica, 2008, 36(6): 1047–1051. doi: 10.3321/j.issn:0372-2112.2008.06.002. [18] WANG Tongzhou and ISOLA P. Understanding contrastive representation learning through alignment and uniformity on the hypersphere[C]. The 37th International Conference on Machine Learning, Vienna, Austria, 2020: 9929–9939. [19] DENG Jiankang, GUO Jia, and XUE Niannan, et al. ArcFace: Additive angular margin loss for deep face recognition[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 4685–4694. doi: 10.1109/CVPR.2019.00482. [20] SCHEIRER W J, ROCHA A, MICHEALS R J, et al. Meta-recognition: The theory and practice of recognition score analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1689–1695. doi: 10.1109/TPAMI.2011.54. [21] 秦博伟, 蒋磊, 许华, 等. 基于RE-GAN的调制信号开集识别算法[J]. 系统工程与电子技术, 2023, 45(10): 3321–3328. doi: 10. 12305/j.issn.1001-506X.2023.10.37.QIN Bowei, JIANG Lei, XU Hua, et al. Open-set recognition algorithm for modulation signal based on RE-GAN[J]. Systems Engineering and Electronics, 2023, 45(10): 3321–3328. doi: 10.12305/j.issn.1001-506X.2023.10.37. [22] SMILKOV D, THORAT N, NICHOLSON C, et al. Embedding projector: Interactive visualization and interpretation of embeddings[J]. arXiv: 1611.05469, 2016. [23] CHANG C C and LIN C J. LIBSVM: A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 27. doi: 10.1145/1961189.1961199. -






 下载:
下载:


 下载:
下载:
