Robust Resource Allocation Algorithm for Low Orbit Satellite Communication System Based on Imperfect CSI
-
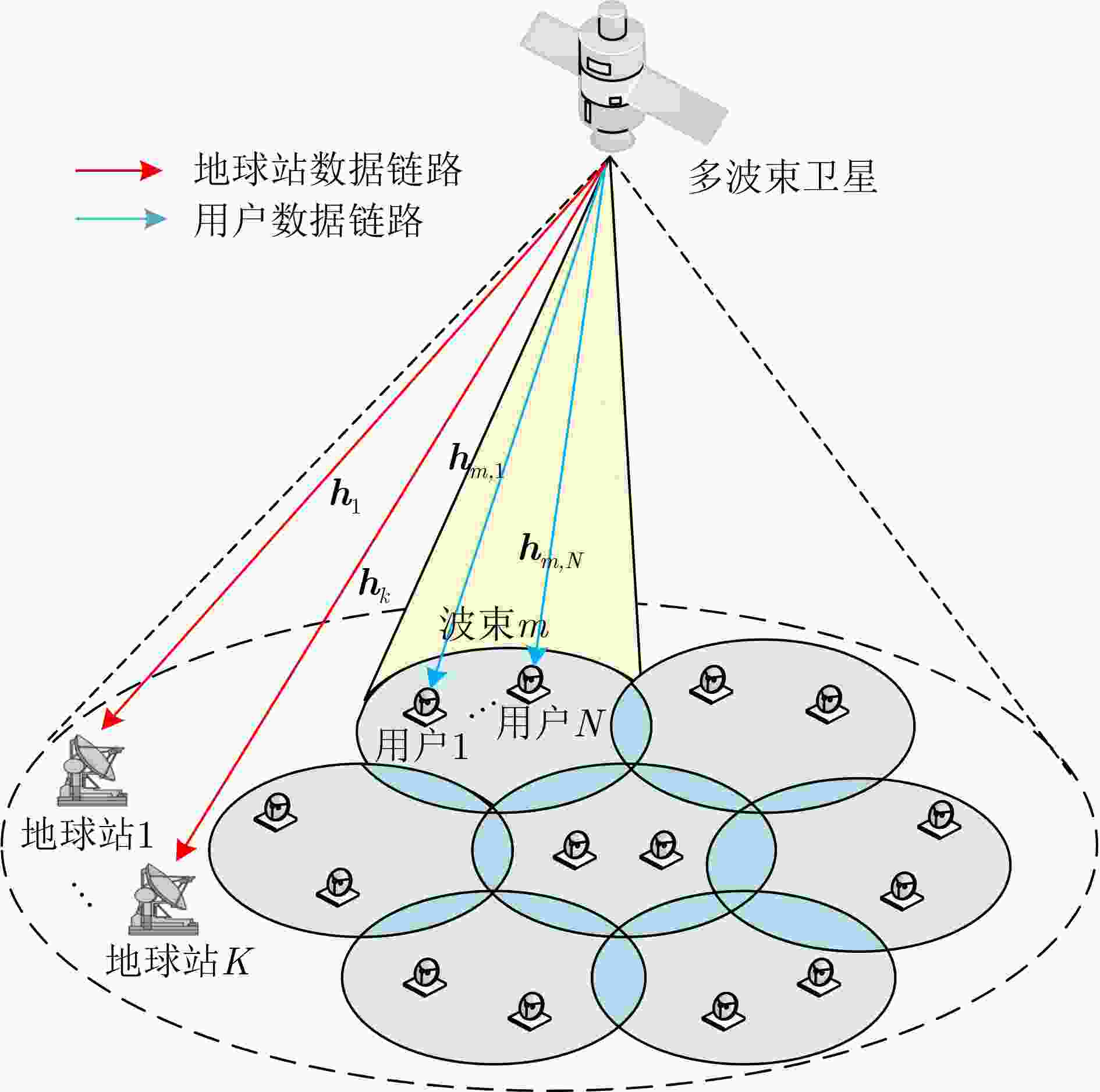
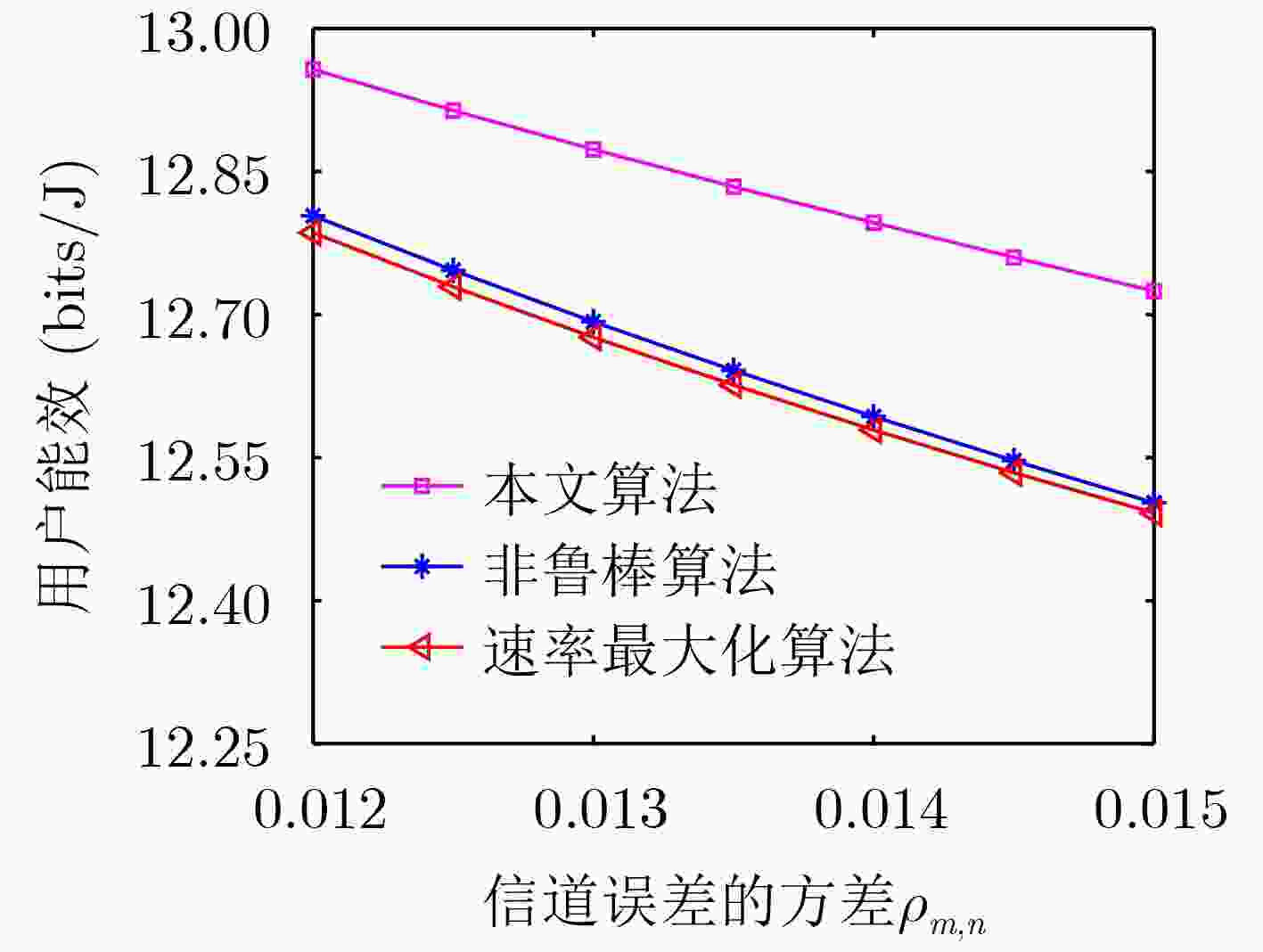
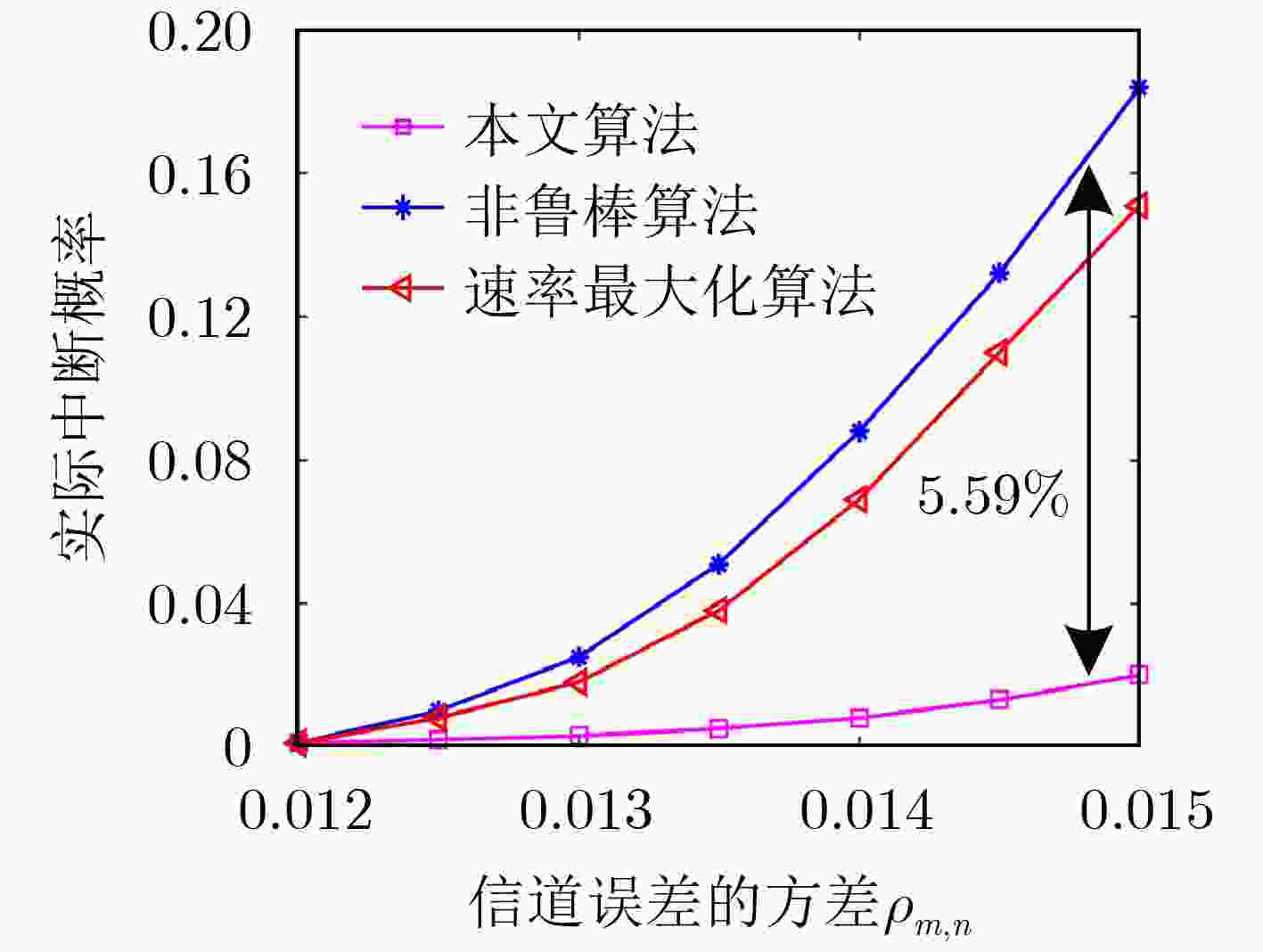
摘要: 为了解决低轨卫星通信系统因资源受限导致的能量与速率不平衡的问题,同时考虑信道不确定性对实际卫星通信系统性能衰退的影响,该文提出一种基于最大化最小能效的鲁棒资源分配算法。首先,考虑每个用户中断速率约束、功率分配系数约束和最大发射功率约束,基于高斯信道不确定性,构建了联合优化卫星波束成形向量与功率分配因子的鲁棒资源分配模型。所描述的问题是一个含参数摄动的非凸、非确定性多项式难问题,很难直接求解。为此,基于丁克尔巴赫、伯恩斯坦不等式、半正定松弛和交替优化等方法将其转化为等价的凸优化问题,并提出一种基于迭代的混合鲁棒波束成形与功率分配算法。仿真结果表明,该文算法具有较好的能效和较强的鲁棒性。Abstract: In order to solve the imbalance problem between power consumption and transmission in low orbit satellite communication systems caused by the limited resource, a robust resource allocation algorithm is proposed to maximize the minimum energy efficiency of multiple users by considering the effect of channel uncertainties on the performance degradation of real satellite communication systems. Firstly, a robust resource allocation model with Gaussian channel uncertainties is formulated by jointly optimizing the beamforming vectors and power allocation factors of the multi-beam satellite, meanwhile the outage rate constraint of each user, the power allocation factor constraint and the maximum transmit power constraint are considered simultaneously. The formulated problem is a non-convex and NP-hard with parametric perturbation, which is difficult to solve it directly. To this end, the original problem is converted into a convex one by using Dinkelbach’s method, Bernstein-type inequality, semi-definite relaxation and the alternating optimization technique, and an iteration-based hybrid robust beamforming and power allocation algorithm is proposed. Simulation results verify that the proposed algorithm has good energy efficiency and strong robustness.
-
1 基于二分法的能效优化策略
初始化$ \eta _{m,n}^ + $和$ \eta _{m,n}^ - $; (1) $f(\eta _{m,n}^ + ) > 0$,$f(\eta _{m,n}^ - ) < 0$; (2) 设置阈值${\chi _1}$和迭代次数${t_1}$,${t_1} = 0$; (3) repeat (4) 更新$ \eta _{m,n}^{({t_1})} \leftarrow (\eta _{m,n}^ + + \eta _{m,n}^ - )/2 $; (5) 求解问题式(17),得到最优解$f(\eta _{m,n}^{({t_1})})$; (6) if $f(\eta _{m,n}^{({t_1})}) \ge 0$ then (7) 更新$ \eta _{m,n}^ + \leftarrow \eta _{m,n}^{({t_1})} $; (8) 否则$ \eta _{m,n}^ - \leftarrow \eta _{m,n}^{({t_1})} $; (9) 结束并更新${t_1} = {t_1} + 1$; (10)直到$ |f(\eta _{m,n}^{({t_1})})| < {\chi _1} $; 获得最优$\eta _{m,n}^ * = \eta _{m,n}^{({t_1})}$。 2 基于迭代的混合鲁棒波束成形和功率分配算法
初始化$K$,$M$, $N$, $\sigma _{m,n}^2$, $ P_{m,n}^{cir} $, $ R_{m,n}^{\min } $, $ R_k^{\min } $, $ {\varepsilon _{m,n}} $, $ {\varepsilon _k} $,
$ {\delta _{m,n}} $,$ {\delta _k} $,$ {\mu _{m,n}} $, $ {\mu _k} $;设置误差精度${\chi _2}$和迭代次数${t_2}$,初始化${t_2} = 0$; (1) repeat (2) 设置初始功率分配系数$\alpha _{m,n}^{({t_2})}$; (3) if $\alpha _{m,n}^{({t_2})} - \alpha _{m,n}^{({t_2} - 1)} \ge {\chi _2}$ then (4) 更新${t_2} = {t_2} + 1$; (5) 否则求解问题(37)获得最优${\boldsymbol{W}}_m^ * = {\boldsymbol{W}}_m^{ {\text{(} }{t_2}{\text{)} } }$; (6) 再求解最优$\alpha _{m,n}^ * $,对${\boldsymbol{W}}_m^ *$使用特征值分解获得${\boldsymbol{w}}_m^ *$; 结束; 表 1 具体仿真参数
参数 值 参数 值 参数 值 卫星 LEO 加性高斯白噪声方差 0.1 雨衰方差(dB) 1.63 卫星高度(km) 1000 玻尔兹曼常数(J/K) 1.38 × 10–23 带宽(MHz) 30 波束数量 3 最大卫星天线增益(dBi) 17 载波频率(GHz) 20 卫星馈电天线数 18 雨衰均值(dB) –2.6 3 dB角 0.4° -
[1] 王宁远, 陈东, 刘亮, 等. 未来低轨信息网络发展与架构展望[J]. 电子与信息学报, 2023, 45(2): 396–406. doi: 10.11999/JEIT211400.WANG Ningyuan, CHEN Dong, LIU Liang, et al. Development trend and architecture prospect of future low-earth-orbit information networks[J]. Journal of Electronics &Information Technology, 2023, 45(2): 396–406. doi: 10.11999/JEIT211400. [2] XU Yongjun, GUI Guan, GACANIN H, et al. A survey on resource allocation for 5G heterogeneous networks: Current research, future trends, and challenges[J]. IEEE Communications Surveys & Tutorials, 2021, 23(2): 668–695. doi: 10.1109/COMST.2021.3059896. [3] XU Yongjun, XIE Hao, WU Qingqing, et al. Robust max-min energy efficiency for RIS-aided HetNets with distortion noises[J]. IEEE Transactions on Communications, 2022, 70(2): 1457–1471. doi: 10.1109/TCOMM.2022.3141798. [4] 孙士勇, 王薇, 顾晨伟, 等. 基于公平效用函数的多波束卫星通信下行链路波束成形算法[J]. 电子与信息学报, 2022, 44(9): 3024–3032. doi: 10.11999/JEIT220409.SUN Shiyong, WANG Wei, GU Chenwei, et al. Beamforming algorithm based on fair utility function for multibeam satellite communication downlink transmission[J]. Journal of Electronics &Information Technology, 2022, 44(9): 3024–3032. doi: 10.11999/JEIT220409. [5] LI Bin, FEI Zesong, CHU Zheng, et al. Robust chance-constrained secure transmission for cognitive satellite–terrestrial networks[J]. IEEE Transactions on Vehicular Technology, 2018, 67(5): 4208–4219. doi: 10.1109/TVT.2018.2791859. [6] JOUDEH H and CLERCKX B. Rate-splitting for max-min fair multigroup multicast beamforming in overloaded systems[J]. IEEE Transactions on Wireless Communications, 2017, 16(11): 7276–7289. doi: 10.1109/TWC.2017.2744629. [7] ZHU Xiangming, JIANG Chunxiao, YIN Liuguo, et al. Cooperative multigroup multicast transmission in integrated terrestrial-satellite networks[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(5): 981–992. doi: 10.1109/JSAC.2018.2832780. [8] ZHANG Yuandong, YIN Liuguo, JIANG Chunxiao, et al. Joint beamforming design and resource allocation for terrestrial-satellite cooperation system[J]. IEEE Transactions on Communications, 2020, 68(2): 778–791. doi: 10.1109/TCOMM.2019.2950022. [9] CHU Jianhang, CHEN Xiaoming, ZHONG Caijun, et al. Robust design for NOMA-based multibeam LEO satellite internet of things[J]. IEEE Internet of Things Journal, 2021, 8(3): 1959–1970. doi: 10.1109/JIOT.2020.3015995. [10] ZHU Yazhou, DELAMOTTE T, and KNOPP A. Geographical NOMA-beamforming in multi-beam satellite-based internet of things[C]. 2019 IEEE Global Communications Conference, Waikoloa, USA, 2019: 1–6. [11] LIN Zhi, LIN Min, WANG Junbo, et al. Joint beamforming and power allocation for satellite-terrestrial integrated networks with nonorthogonal multiple access[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 657–670. doi: 10.1109/JSTSP.2019.2899731. [12] YOU Li, LIU Ao, WANG Wenjin, et al. Outage constrained robust multigroup multicast beamforming for multi-beam satellite communication systems[J]. IEEE Wireless Communications Letters, 2019, 8(2): 352–355. doi: 10.1109/LWC.2018.2872710. [13] XIAO Yi, MISHRA D, YUAN Jinhong, et al. Proportionally fair robust beamforming for multicast multibeam satellite systems[J]. IEEE Communications Letters, 2022, 26(1): 128–132. doi: 10.1109/LCOMM.2021.3118567. [14] YAN Yan, AN Kang, ZHANG Bangning, et al. Outage-constrained robust multigroup multicast beamforming for satellite-based internet of things coexisting with terrestrial networks[J]. IEEE Internet of Things Journal, 2021, 8(10): 8159–8172. doi: 10.1109/JIOT.2020.3042831. [15] WANG Wenjin, GAO Linna, DING Rui, et al. Resource efficiency optimization for robust beamforming in multi-beam satellite communications[J]. IEEE Transactions on Vehicular Technology, 2021, 70(7): 6958–6968. doi: 10.1109/TVT.2021.3087744. [16] WANG Zining, LIN Min, SUN Shiyong, et al. Robust beamforming for enhancing user fairness in multibeam satellite systems with NOMA[J]. IEEE Transactions on Vehicular Technology, 2022, 71(1): 1010–1014. doi: 10.1109/TVT.2021.3124928. [17] VÁZQUEZ M Á, PÉREZ-NEIRA A, CHRISTOPOULOS D, et al. Precoding in multibeam satellite communications: Present and future challenges[J]. IEEE Wireless Communications, 2016, 23(6): 88–95. doi: 10.1109/MWC.2016.1500047WC. [18] XU Yongjun, ZHAO Xiaohui, and LIANG Yingchang. Robust power control and beamforming in cognitive radio networks: A survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 1834–1857. doi: 10.1109/COMST.2015.2425040. [19] DINKELBACH W. On nonlinear fractional programming[J]. Management Science, 1967, 13(7): 492–498. doi: 10.1287/MNSC.13.7.492. [20] BECHAR I. A Bernstein-type inequality for stochastic processes of quadratic forms of Gaussian variables[J]. arXiv: 0909.3595, 2009. [21] LUO Zhiquan, MA W K, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27(3): 20–34. doi: 10.1109/MSP.2010.936019. [22] WANG Kunyu, SO A M C, CHANG T H, et al. Outage constrained robust transmit optimization for multiuser MISO downlinks: Tractable approximations by conic optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5690–5705. doi: 10.1109/TSP.2014.2354312. [23] LU Weixin, AN Kang, and LIANG Tao. Robust beamforming design for sum secrecy rate maximization in multibeam satellite systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1568–1572. doi: 10.1109/TAES.2019.2905306. -





 下载:
下载:


 下载:
下载:
