基于动态规整与改进变分自编码器的异常电池在线检测方法

郭铁峰; 贺建军; 申帅; 王翔; 张彬汉

doi:10.11999/JEIT230084

基于动态规整与改进变分自编码器的异常电池在线检测方法

doi: 10.11999/JEIT230084

中南大学自动化学院长沙 410083

基金项目: 国家重点研发计划(2020YFB1710600)

详细信息

作者简介:
郭铁峰：男，博士生，研究方为智能检测与控制、机器学习等

贺建军：男，教授，博士生导师，研究方向为智能检测与控制、机器学习、系统建模与优化控制等

申帅：男，博士生，研究方向为智能检测、自动控制和机器学习

王翔：男，博士生，研究方向为稀疏表示、深度学习等

张彬汉：男，硕士生，研究方向为稀疏表示、深度学习等

通讯作者:
贺建军　jjhe@csu.edu.cn

中图分类号: TN911; TP183
计量
- 文章访问数: 611
- HTML全文浏览量: 355
- PDF下载量: 89
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-22
- 修回日期: 2023-06-16
- 网络出版日期: 2023-06-28
- 刊出日期: 2024-02-29

Abnormal Battery On-line Detection Method Based on Dynamic Time Warping and Improved Variational Auto-Encoder

School of Automation, Central South University, Changsha 410083, China

Funds: National Key R&D Program of China (2020YFB1710600)

摘要

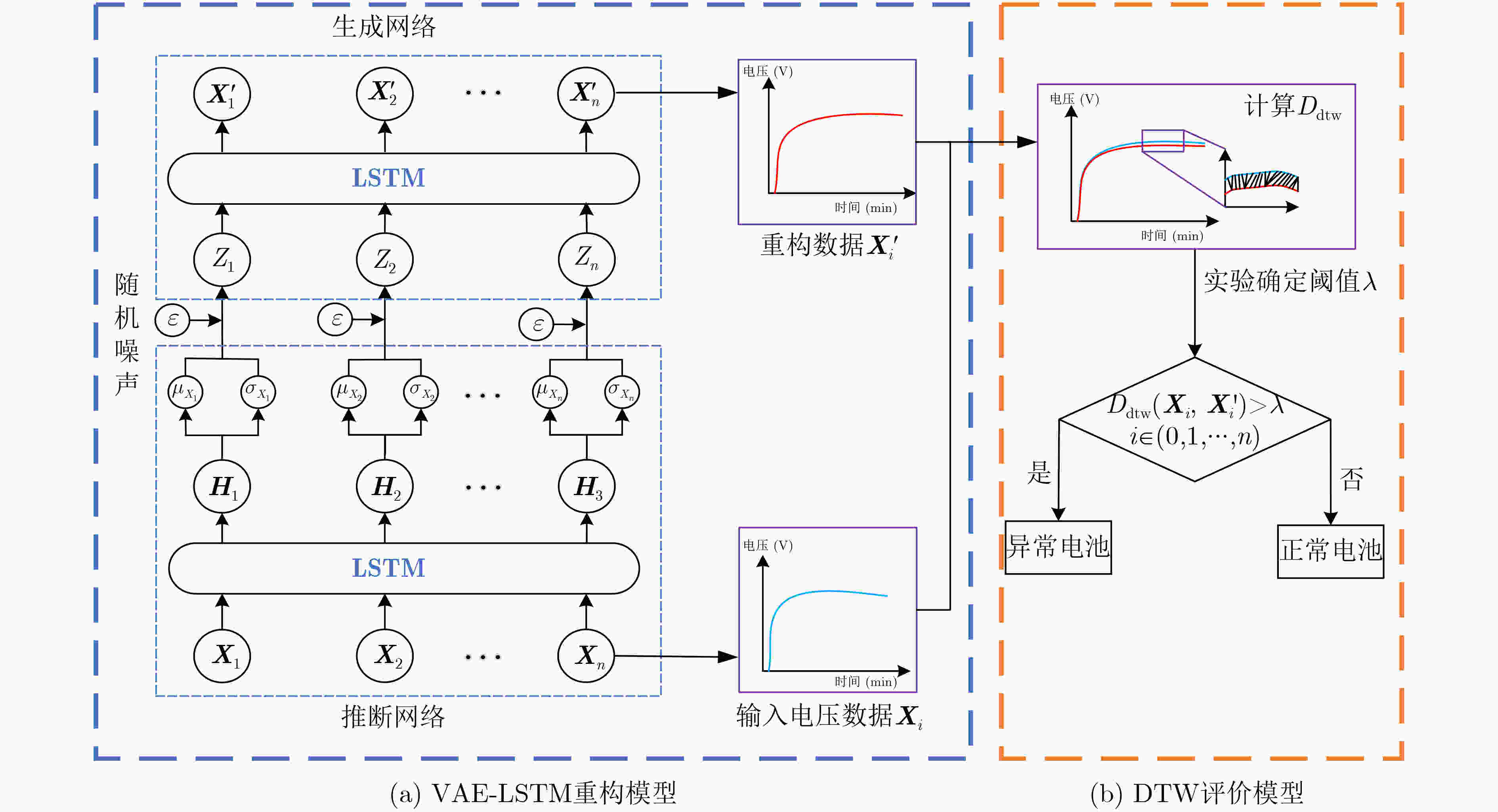
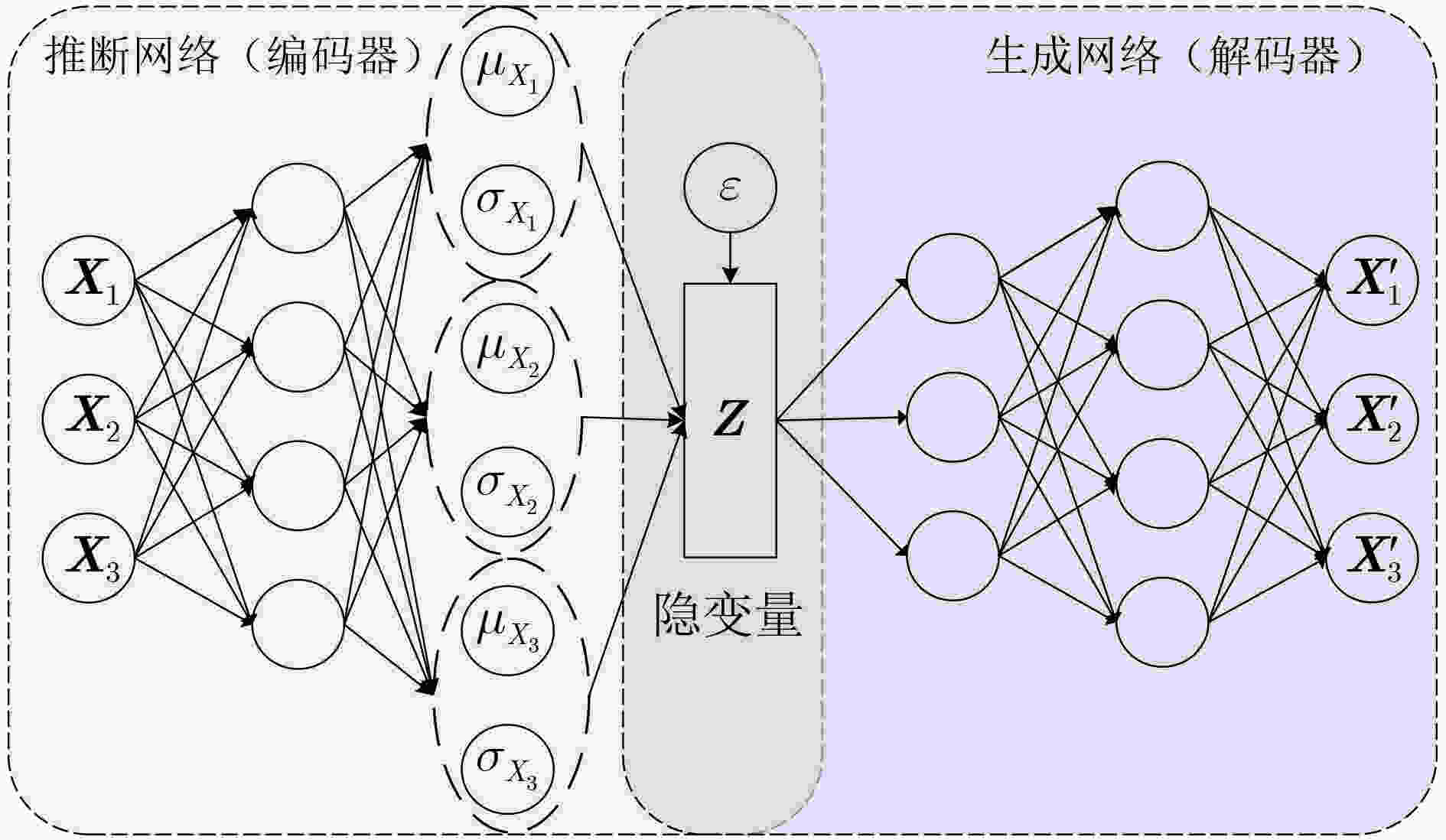
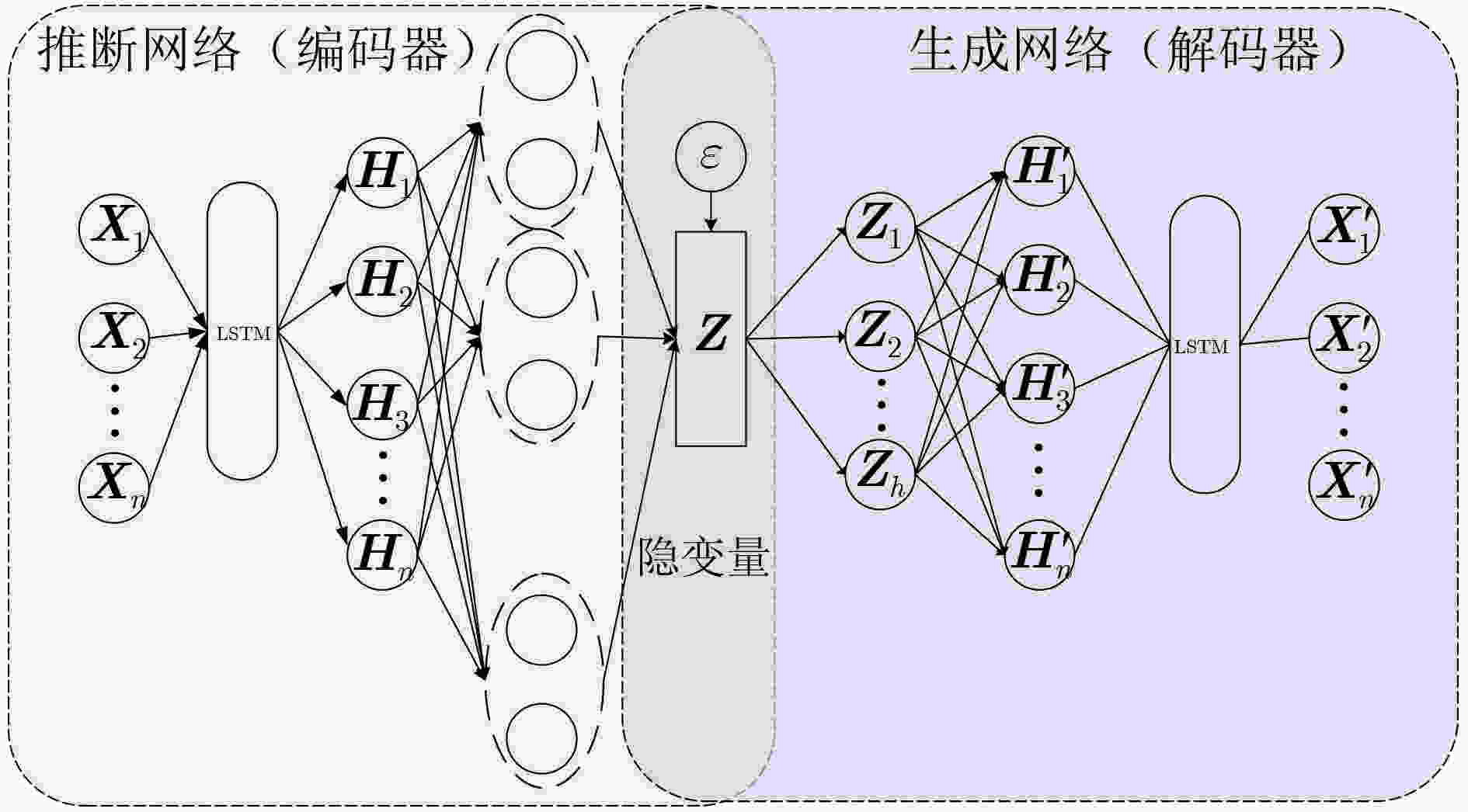
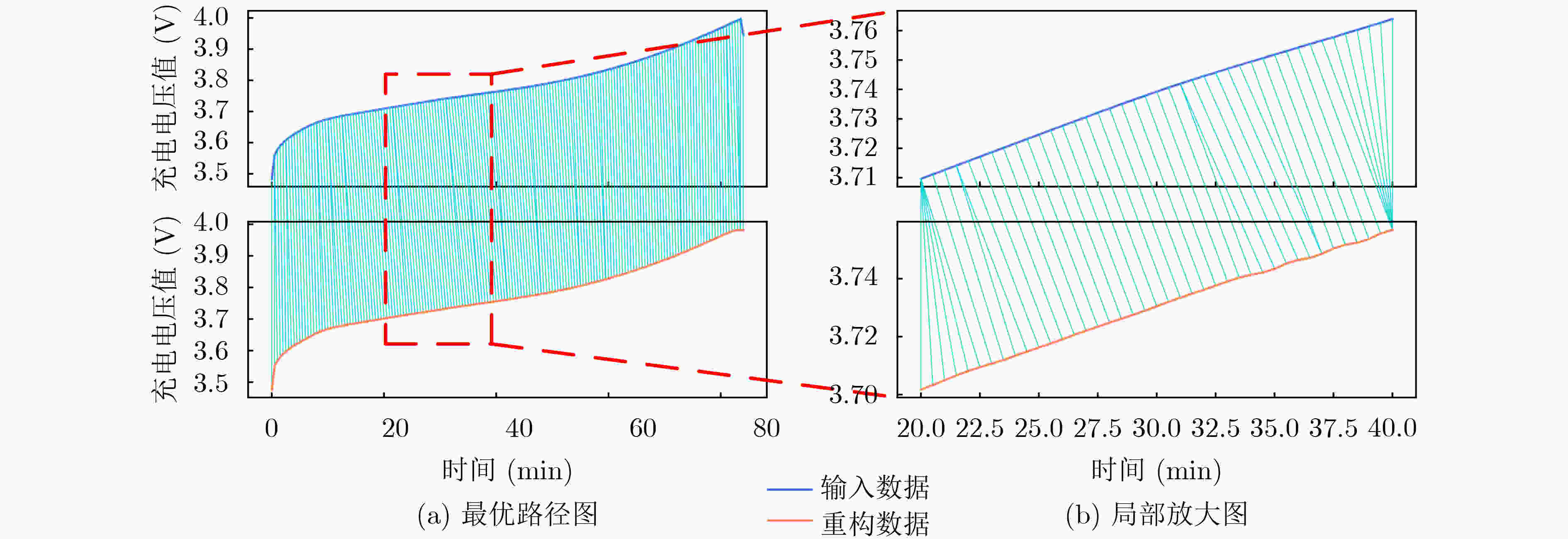
摘要: 针对电池生产成组过程中，传统异常检测方法对混入的容量及压差异常电池检测精度低及生产结束后离线异常检测方法效率低等问题，该文提出一种集合长短期记忆变分自编码器与动态时间规整评价的锂电池异常在线检测方法(VAE-LSTM-DTW)，实现了异常电池的在线检测，避免了离线异常检测所造成的时间和能源的浪费。该方法首先将长短期记忆网络(LSTM)引入变分自编码器(VAE)模型，训练电池时序数据重构模型；其次，在电池异常检测的度量标准中引入动态时间规整值(DTW)，并基于贝叶斯寻优获得最优检测阈值，对每个单体电池重构数据的动态规整值进行异常辨别。实验结果表明，相较该领域传统异常检测方法，VAE-LSTM-DTW模型性能优越，查准率和F1值都得到了较大的提升，具有较高的有效性和实用性。
- 锂电池 /
- 异常检测 /
- 变分自编码器 /
- 动态时间规整 /
- 长短期记忆网络 /
- 贝叶斯优化
Abstract: In the process of battery production, the traditional detection accuracy of abnormal batteries is poor, and the offline anomaly detection method after production is inefficient. To solve these problems, a lithium battery anomaly online detection method integrating Long Short-Term Memory Variational AutoEncoder and Dynamic Time Warping evaluation (VAE-LSTM-DTW) is proposed, which realizes the online detection of abnormal battery conditions and prevents the time and energy wastage caused by offlize anomaly detection. Firstly, the Long Short-Term Memory (LSTM) is introduced into the Variational Auto-Encoder (VAE) model to train the battery time series reconstruction model. Secondly, in battery anomaly detection, the Dynamic Time Warping value (DTW) is introduced into the evaluation index, and the optimal detection threshold is obtained based on Bayesian optimization, and the dynamic warping value of each single battery reconstruction data is abnormally identified. The experimental results indicate that, compared with the traditional anomaly detection methods in this field, the VAE-LSTM-DTW model has superior performance, the accuracy rate and F1-score have been greatly improved, and it has high effectiveness and practicability.
- Lithium battery /
- Anomaly detection /
- Variational Auto-Encoder(VAE) /
- Dynamic Time Warping(DTW) /
- Long Short-Term Memory(LSTM) /
- Bayesian optimization

HTML全文

图 1 锂电池异常检测模型结构图

下载: 全尺寸图片幻灯片

图 2 变分自编码器模型结构图

下载: 全尺寸图片幻灯片

图 3 VAE-LSTM模型结构图

下载: 全尺寸图片幻灯片

图 4 DTW最优路径

下载: 全尺寸图片幻灯片

图 5 生产现场化成分容设备图

下载: 全尺寸图片幻灯片

图 6 原始数据集曲线图

下载: 全尺寸图片幻灯片

图 7 重构模型训练损失函数变化

下载: 全尺寸图片幻灯片

图 8 异常电池充电曲线分类图

下载: 全尺寸图片幻灯片

图 9 DTW分布箱线图

下载: 全尺寸图片幻灯片

图 10 阈值寻优流程图

下载: 全尺寸图片幻灯片

图 11 4类度量标准检测结果分布对比图

下载: 全尺寸图片幻灯片

图 12 消融实验异常检测结果分布对比图

下载: 全尺寸图片幻灯片

表 1 数据集构建情况表

数据集分类	正常电池 (个 )	正常占比(%)	异常电池(个)	异常占比(%)
重构训练集	4 000	100	0	0
评价阈值训练集	4 000	50	4 000	50
测试集	4 000	50	4 000	50

下载: 导出CSV

表 2 阈值确定10折验证实验结果表

实验轮次	阈值训练集		阈值测试集	平均最优阈值
实验轮次	最优阈值	F1值	F1值	平均最优阈值
1	0.2175	0.9776	0.9749	0.2169
2	0.2169	0.9766	0.9836
3	0.2159	0.9770	0.9810
4	0.2164	0.9779	0.9710
5	0.2169	0.9773	0.9773
6	0.2159	0.9773	0.9774
7	0.2171	0.9780	0.9707
8	0.2176	0.9776	0.9748
9	0.2179	0.9762	0.9887
10	0.2169	0.9777	0.9735

下载: 导出CSV

表 3 重构效果度量标准对比实验

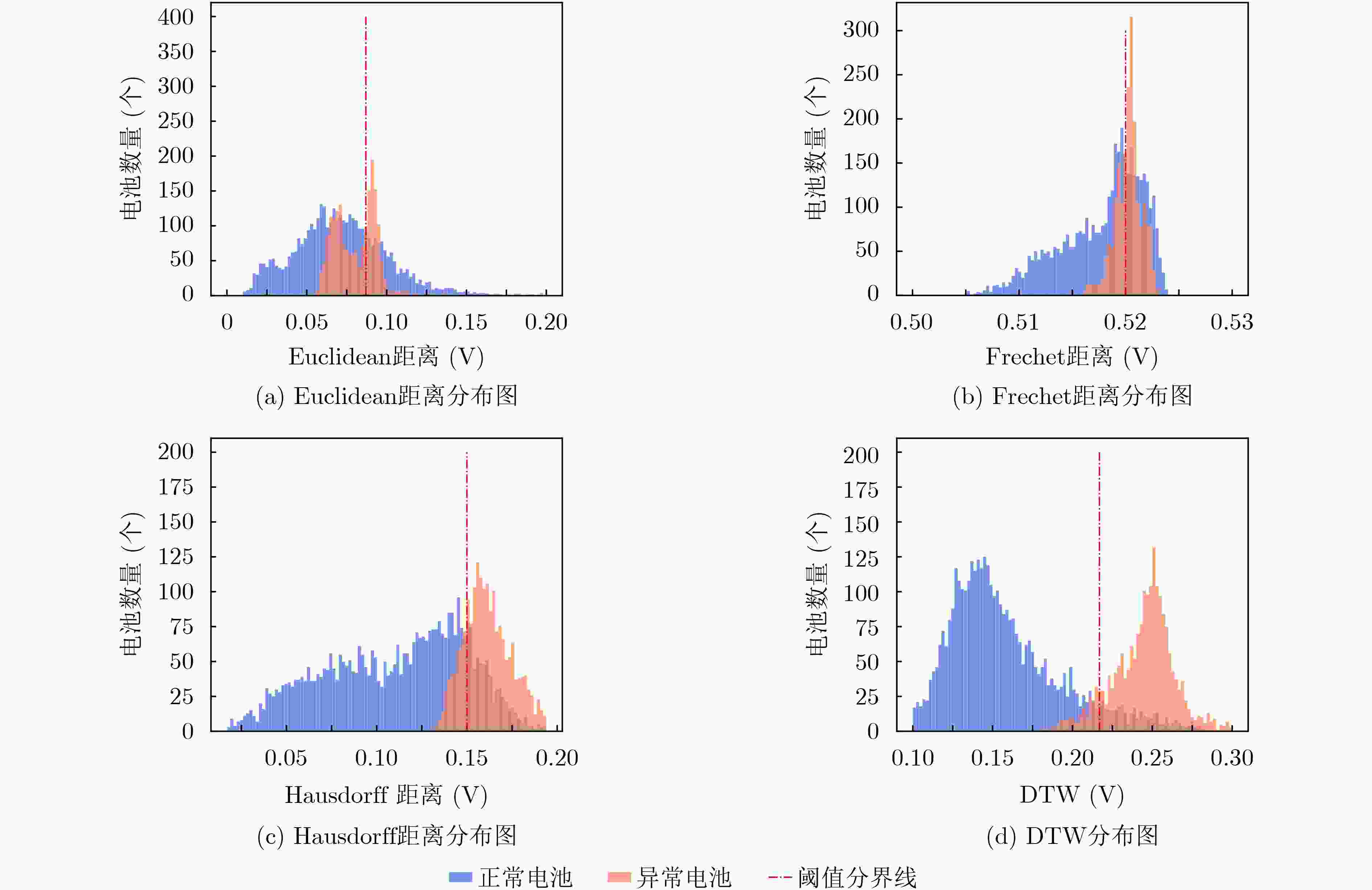
距离	准确率(%)	查准率(%)	召回率(%)	F1值	阈值
Euclidean	62.8	71.9	72.6	0.72	0.0873
Frechet	65.0	78.6	65.3	0.71	0.5202
Hausdorff	82.7	89.7	83.7	0.87	0.0150
DTW	91.2	95.1	91.7	0.93	0.2169

下载: 导出CSV

表 4 机器学习模型异常检测对比实验

模型	准确率(%)	查准率(%)	召回率(%)	F1值
OCSVM	67.2	61.0	95.4	0.744
LOF	68.2	63.0	88.7	0.736
IForest	62.4	57.1	98.0	0.725
VAE-LSTM-DTW	91.1	94.9	91.7	0.933

下载: 导出CSV

表 5 模型异常检测消融实验结果

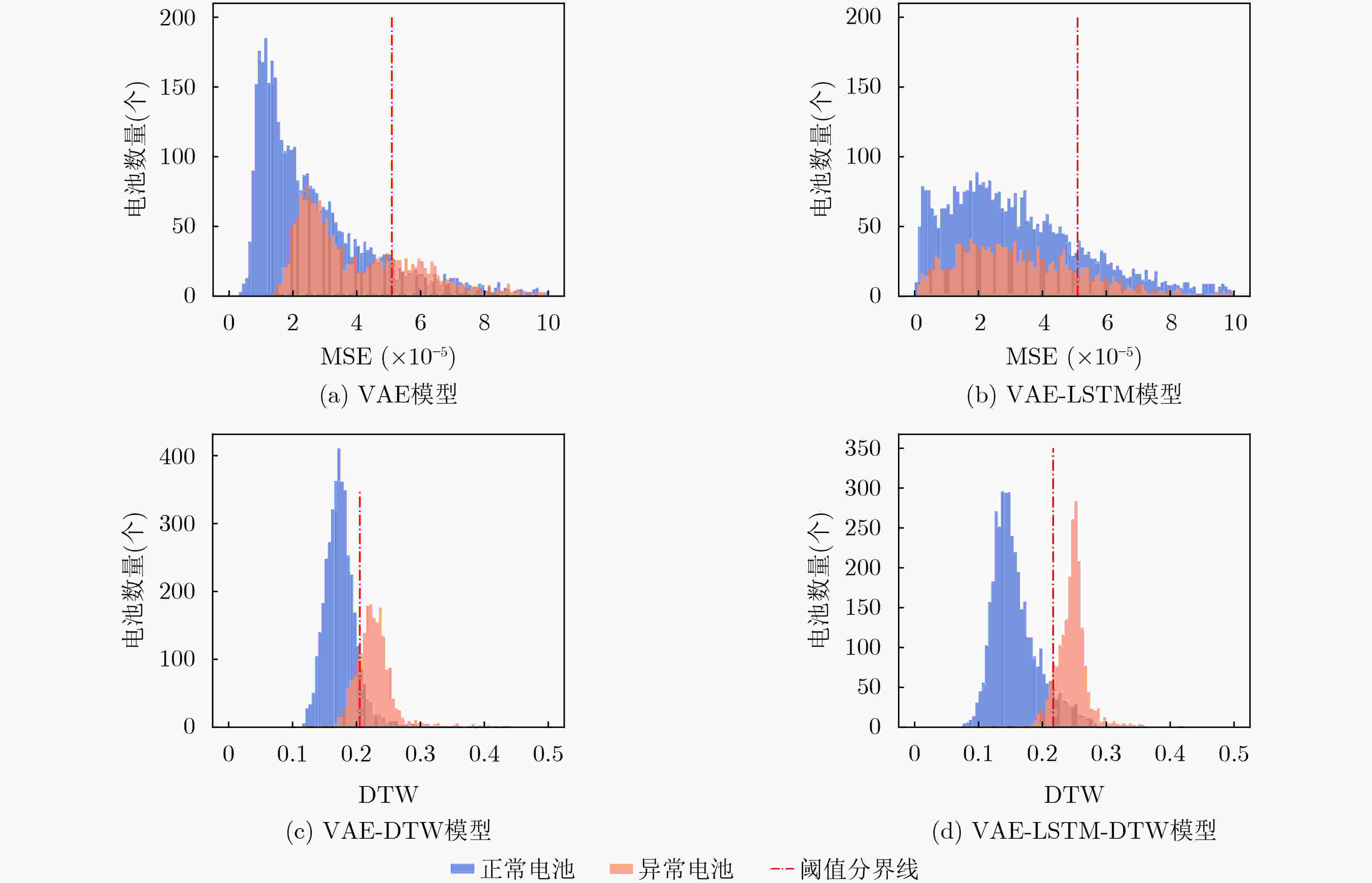
模型	准确率(%)	查准率(%)	召回率(%)	F1值	阈值	单体电池检测时间(s)
VAE	68.9	71.9	87.5	0.79	5.1× 10^–5	0.002
VAE-LSTM	73.2	76.0	83.4	0.79	4.3 × 10^–5	0.014
VAE-DTW	87.8	90.6	91.2	0.91	0.2052	0.075
VAE-LSTM-DTW	91.1	94.9	91.7	0.93	0.2169	0.084

下载: 导出CSV

参考文献(20)

[1]	肖健夫, 孙瑞, 闵婕, 等. 锂离子动力电池系统故障检测[J]. 电源技术, 2021, 45(6): 736–739,790. doi: 10.3969/j.issn.1002-087X.2021.06.012. XIAO Jianfu, SUN Rui, MIN Jie, et al. Fault detection of lithium-ion power battery system[J]. Chinese Journal of Power Sources, 2021, 45(6): 736–739,790. doi: 10.3969/j.issn.1002-087X.2021.06.012.
[2]	马速良, 武亦文, 李建林, 等. 聚类分析架构下基于遗传算法的电池异常数据检测方法[J]. 电网技术, 2023, 47(2): 859–867. doi: 10.13335/j.1000-3673.pst.2021.1871. MA Suliang, WU Yiwen, LI Jianlin, et al. Anomaly detection for battery data based on genetic algorithm under cluster analysis framework[J]. Power System Technology, 2023, 47(2): 859–867. doi: 10.13335/j.1000-3673.pst.2021.1871.
[3]	JIN Ruochen, WEI Bo, LUO Yongmei, et al. Blockchain-based data collection with efficient anomaly detection for estimating battery state-of-health[J]. IEEE Sensors Journal, 2021, 21(12): 13455–13465. doi: 10.1109/JSEN.2021.3066785.
[4]	SAXENA S, KANG M, XING Y J, et al. Anomaly detection during lithium-ion battery qualification testing[C]. 2018 IEEE International Conference on Prognostics and Health Management, Seattle, USA, 2018: 1–6.
[5]	董书琴, 张斌. 基于深度特征学习的网络流量异常检测方法[J]. 电子与信息学报, 2020, 42(3): 695–703. doi: 10.11999/JEIT190266. DONG Shuqin and ZHANG Bin. Network traffic anomaly detection method based on deep features learning[J]. Journal of Electronics &Information Technology, 2020, 42(3): 695–703. doi: 10.11999/JEIT190266.
[6]	KINGMA D P and WELLING M. Auto-encoding variational Bayes[C]. The 2nd International Conference on Learning Representations, Banff, Canada, 2014.
[7]	GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Communications of the ACM, 2020, 63(11): 139–144. doi: 10.1145/3422622.
[8]	AN J and CHO S. Variational autoencoder based anomaly detection using reconstruction probability[J]. Special Lecture on IE, 2015, 2(1): 1–18.
[9]	秦婉亭, 老松杨, 汤俊, 等. 基于变分自编码器的飓风轨迹异常检测方法[J]. 系统仿真学报, 2021, 33(9): 2191–2201. doi: 10.16182/j.issn1004731x.joss.20-0369. QIN Wanting, LAO Songyang, TANG Jun, et al. Hurricane trajectory outlier detection method based on variational auto-encode[J]. Journal of System Simulation, 2021, 33(9): 2191–2201. doi: 10.16182/j.issn1004731x.joss.20-0369.
[10]	常吉亮, 谢磊, 赵建伟, 等. 基于VAE-LSTM模型的航迹异常检测算法[J]. 交通信息与安全, 2020, 38(6): 1–8. doi: 10.3963/j.jssn.1674-4861.2020.06.001. CHANG Jiliang, XIE Lei, ZHAO Jianwei, et al. An anomaly detection algorithm for ship trajectory data based on VAE-LSTM model[J]. Journal of Transport Information and Safety, 2020, 38(6): 1–8. doi: 10.3963/j.jssn.1674-4861.2020.06.001.
[11]	ZHOU Chong and PAFFENROTH R C. Anomaly detection with robust deep autoencoders[C]. The 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, Canada, 2017: 665–674.
[12]	LI Junying, REN Weijie, and HAN Min. Variational auto-encoders based on the shift correction for imputation of specific missing in multivariate time series[J]. Measurement, 2021, 186: 110055. doi: 10.1016/j.measurement.2021.110055.
[13]	HOCHREITER S and SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735.
[14]	BERNDT D J and CLIFFORD J. Using dynamic time warping to find patterns in time series[C]. The 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, USA, 1994: 359–370.
[15]	SHAHRIARI B, SWERSKY K, WANG Ziyu, et al. Taking the human out of the loop: A review of Bayesian optimization[J]. Proceedings of the IEEE, 2016, 104(1): 148–175. doi: 10.1109/JPROC.2015.2494218.
[16]	FRÉCHET M M. Sur quelques points du calcul fonctionnel[J]. Rendiconti del Circolo Matematico di Palermo (1884–1940), 1906, 22(1): 1–72. doi: 10.1007/BF03018603.
[17]	TAHA A A and HANBURY A. An efficient algorithm for calculating the exact Hausdorff distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(11): 2153–2163. doi: 10.1109/TPAMI.2015.2408351.
[18]	SCHÖLKOPF B, PLATT J C, SHAWE-TAYLOR J, et al. Estimating the support of a high-dimensional distribution[J]. Neural Computation, 2001, 13(7): 1443–1471. doi: 10.1162/089976601750264965.
[19]	LI Lu, HUANG Liusheng, YANG Wei, et al. Privacy-preserving LOF outlier detection[J]. Knowledge and Information Systems, 2015, 42(3): 579–597. doi: 10.1007/s10115-013-0692-0.
[20]	王诚, 狄萱. 孤立森林算法研究及并行化实现[J]. 计算机技术与发展, 2021, 31(6): 13–18. doi: 10.3969/j.issn.1673-629X.2021.06.003. WANG Cheng and DI Xuan. Research and parallelization of isolation forest algorithm[J]. Computer Technology and Development, 2021, 31(6): 13–18. doi: 10.3969/j.issn.1673-629X.2021.06.003.