Chaotic Power System Control Based on Improved Adaptive Synergetic Control Method
-
摘要: 针对4阶混沌电力系统,该文提出一种具有快速收敛特性的自适应协同控制方案。首先基于Lyapunov稳定性定理和全局快速收敛理论,设计了一种具有快速收敛特性的协同控制器,该控制器可使宏变量快速到达不变流形并可以得到平滑无抖振的控制输入,实现宏变量的精确收敛。然后将所设计的控制器应用于4阶电力系统的混沌控制中。由于电力系统中的能量过剩会引起混沌振荡,在控制回路中引入储能装置,通过控制储能装置吸收电力系统中多余的有功功率来抑制其混沌振荡。在此基础上通过设计自适应律,消除了控制器设计过程中出现的复杂项,增加了控制器的实用性。最后通过数值仿真,验证了该控制方案的有效性与优越性。Abstract: An adaptive cooperative control scheme with fast convergence characteristics is proposed for a four-dimensional chaotic power system. Firstly, based on the Lyapunov stability theorem and global fast convergence theory, a cooperative controller with fast convergence property is designed. The controller can make the macro variables reach the invariant manifold quickly and can obtain smooth and chatter-free control inputs to achieve the exact convergence of macro variables. The designed controller is then applied to the chaotic control of a four-dimensional power system. Since excess energy in the power system can cause chaotic oscillations, an energy storage device is introduced in the control loop. The chaotic oscillations are suppressed by making the energy storage device to absorb the excess active power in the power system. The complex terms that appear in the controller design process are eliminated through the adaptive law, so the practicality of the controller is increased. Finally, the effectiveness and superiority of the control method are verified by numerical simulation.
-
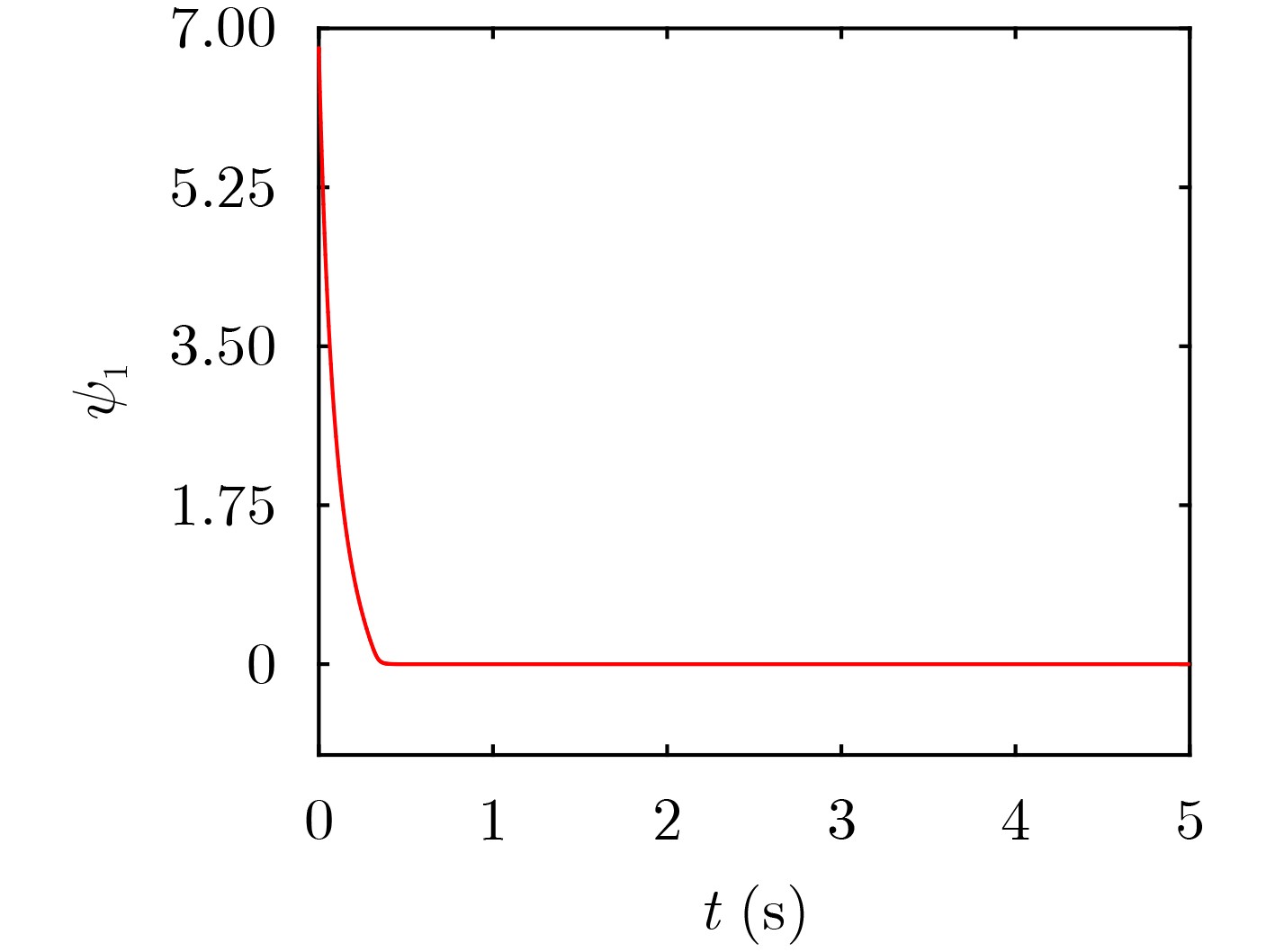
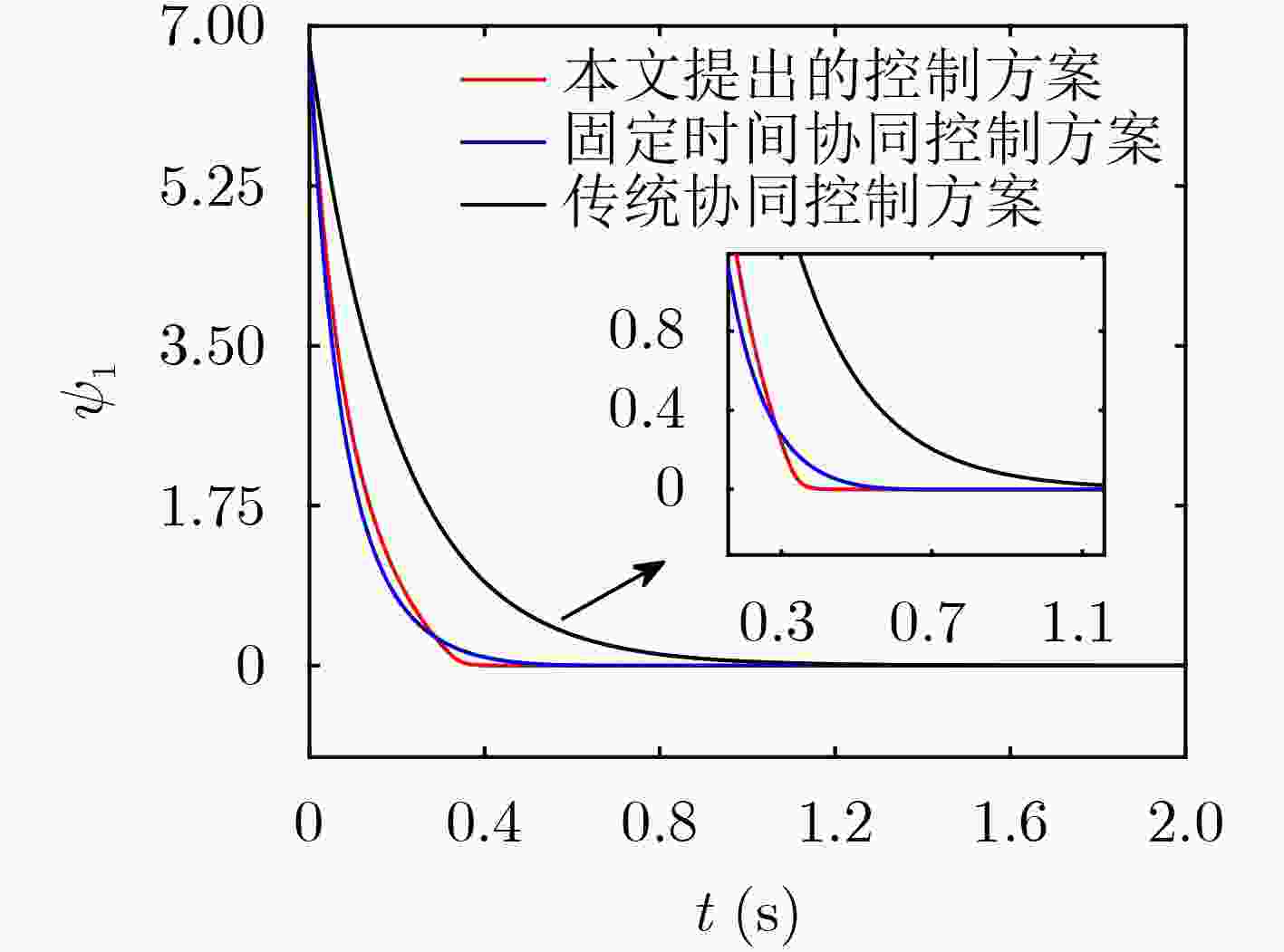
表 1 宏变量$ {\psi _1} $在3种控制方法下的收敛时间对比(s)
控制方案 宏变量${\psi _1}$的收敛时间 传统协同控制方案 1.25 固定时间协同控制方案 0.62 本文提出的控制方案 0.41 -
[1] JING Zhiujun, XU Dashun, CHANG Yu, et al. Bifurcations, chaos, and system collapse in a three node power system[J]. International Journal of Electrical Power & Energy Systems, 2003, 25(6): 443–461. doi: 10.1016/s0142-0615(02)00130-8. [2] ZHU Darui, ZHANG Wenchao, LIU Chongxin, et al. Fractional-order hyperbolic tangent sliding mode control for chaotic oscillation in power system[J]. Mathematical Problems in Engineering, 2021, 2021: 6691941. doi: 10.1155/2021/6691941. [3] 徐敏, 康哲, 刘早富. 基于观测器的混沌电力系统PI固定时间自适应滑模控制[J]. 电力系统保护与控制, 2022, 50(19): 146–157. doi: 10.19783/j.cnki.pspc.211651.XU Min, KANG Zhe, and LIU Zaofu. Observer-based PI fixed time adaptive sliding mode control for chaotic power systems[J]. Power System Protection and Control, 2022, 50(19): 146–157. doi: 10.19783/j.cnki.pspc.211651. [4] 闵富红, 王耀达, 窦一平. 含励磁环节的分数阶电力系统混沌振荡分析与控制[J]. 电子与信息学报, 2017, 39(8): 1993–1999. doi: 10.11999/JEIT161398.MIN Fuhong, WANG Yaoda, and DOU Yiping. Analysis and control of chaotic oscillation in fractional-order power system with excitation model[J]. Journal of Electronics &Information Technology, 2017, 39(8): 1993–1999. doi: 10.11999/JEIT161398. [5] KUMAR M and SINGH P P. Chaos control of a four-dimensional fundamental power system using pole placement-based proportional integral sliding mode control[J]. International Journal of Automation and Control, 2019, 13(6): 679–697. doi: 10.1504/IJAAC.2019.102671. [6] HUANG Sunhua, ZHOU Bin, BU Siqi, et al. Robust fixed-time sliding mode control for fractional-order nonlinear hydro-turbine governing system[J]. Renewable Energy, 2019, 139: 447–458. doi: 10.1016/j.renene.2019.02.095. [7] 王聪, 张宏立, 马萍. 基于有限时间函数投影的电力系统混沌控制[J]. 振动与冲击, 2021, 40(14): 125–131. doi: 10.13465/j.cnki.jvs.2021.14.017.WANG Cong, ZHANG Hongli, and MA Ping. Finite-time function projective synchronization control method for a chaotic power system[J]. Journal of Vibration and Shock, 2021, 40(14): 125–131. doi: 10.13465/j.cnki.jvs.2021.14.017. [8] ALRIFAI M T and ZRIBI M. Sliding mode control of chaos in a single machine connected to an infinite bus power system[J]. Mathematical Problems in Engineering, 2018, 2018: 2703684. doi: 10.1155/2018/2703684. [9] AI Chunyu, HE Shan, and FAN Xiaochao. Parameter estimation of fractional-order chaotic power system based on lens imaging learning strategy state transition algorithm[J]. IEEE Access, 2023, 11: 13724–13737. doi: 10.1109/access.2023.3243081. [10] KOPELL N and WASHBURN R. Chaotic motions in the two-degree-of-freedom swing equations[J]. IEEE Transactions on Circuits and Systems, 1982, 29(11): 738–746. doi: 10.1109/TCS.1982.1085094. [11] MA Caoyuan, WU Wenbei, LI Zhijie, et al. Adaptive fixed-time stability control and parameters identification for chaotic oscillation in second order power system[J]. Mathematical Problems in Engineering, 2018, 2018: 2162483. doi: 10.1155/2018/2162483. [12] DARVISH FALEHI A. An optimal second-order sliding mode based inter‐area oscillation suppressor using chaotic whale optimization algorithm for doubly fed induction generator[J]. International Journal of Numerical Modelling:Electronic Networks, Devices and Fields, 2022, 35(2): e2963. doi: 10.1002/jnm.2963. [13] GAO Wen, XIAO Haifeng, MA Zhao, et al. Fuzzy-based sliding mode control of chaotic oscillation in power system[J]. IOP Conference Series:Materials Science and Engineering, 2020, 782(3): 032035. doi: 10.1088/1757-899x/782/3/032035. [14] 于永进, 王家斌, 王艳. 基于自适应全局滑模的电力系统混沌振荡控制[J]. 电力系统保护与控制, 2019, 47(16): 43–49. doi: 10.19783/j.cnki.pspc.181198.YU Yongjin, WANG Jiabin, and WANG Yan. Chaotic oscillation control in power system based on adaptive total sliding mode[J]. Power System Protection and Control, 2019, 47(16): 43–49. doi: 10.19783/j.cnki.pspc.181198. [15] NI Junkang, LIU Ling, LIU Chongxin, et al. Fast fixed-time nonsingular terminal sliding mode control and its application to chaos suppression in power system[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2017, 64(2): 151–155. doi: 10.1109/tcsii.2016.2551539. [16] LV Yanling, ZHANG Yuchen, LIU Qi, et al. Sliding mode control of two-parameter fourth-order chaos model of power system[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2022, 69(12): 4849–4853. doi: 10.1109/tcsii.2021.3062466. [17] 赵辉, 袁大壮, 王红君, 等. 电力系统有限时间稳定控制策略[J]. 控制与决策, 2018, 33(12): 2283–2288. doi: 10.13195/j.kzyjc.2017.0796.ZHAO Hui, YUAN Dazhuang, WANG Hongjun, et al. Finite time stability control strategy for power system[J]. Control and Decision, 2018, 33(12): 2283–2288. doi: 10.13195/j.kzyjc.2017.0796. [18] GAO Hongliang, ZHANG Hongcong, and LI Xiaoling. Sliding mode control of the vehicle speed system based on LMIs[J]. Complexity, 2021, 2021: 5535213. doi: 10.1155/2021/5535213. [19] MOU Fangli, WU Dan, and DONG Yunfei. Disturbance rejection sliding mode control for robots and learning design[J]. Intelligent Service Robotics, 2021, 14(2): 251–269. doi: 10.1007/s11370-021-00360-z. [20] 王定胜, 张宏立, 王聪, 等. 基于浸入与不变原理的电力系统混沌振荡分析与控制[J]. 振动与冲击, 2022, 41(4): 142–149. doi: 10.13465/j.cnki.jvs.2022.04.019.WANG Dingsheng, ZHANG Hongli, WANG Cong, et al. Analysis and control of power system chaotic oscillation based on the immersion and invariance principle[J]. Journal of Vibration and Shock, 2022, 41(4): 142–149. doi: 10.13465/j.cnki.jvs.2022.04.019. [21] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407–418. doi: 10.3969/j.issn.1000-8152.2007.03.015.LIU Jinkun and SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory &Applications, 2007, 24(3): 407–418. doi: 10.3969/j.issn.1000-8152.2007.03.015. [22] AL-HUSSEIN A B A, TAHIR F R, OUANNAS A, et al. Chaos suppressing in a three-buses power system using an adaptive synergetic control method[J]. Electronics, 2021, 10(13): 1532. doi: 10.3390/electronics10131532. [23] NI Junkang, LIU Chongxin, LIU Kai, et al. Variable speed synergetic control for chaotic oscillation in power system[J]. Nonlinear Dynamics, 2014, 78(1): 681–690. doi: 10.1007/s11071-014-1468-0. [24] SANTI E, MONTI A, LI D, et al. Synergetic control for power electronics applications: A comparison with the sliding mode approach[J]. Journal of Circuits, Systems and Computers, 2004, 13(4): 737–760. doi: 10.1142/s0218126604001520. [25] 王江彬, 刘崇新. 4阶混沌电力系统的协同控制方法[J]. 西安交通大学学报, 2020, 54(1): 26–31. doi: 10.7652/xjtuxb202001004.WANG Jiangbin and LIU Chongxin. Synergetic control method for four-dimensional chaotic power system[J]. Journal of Xi’an Jiaotong University, 2020, 54(1): 26–31. doi: 10.7652/xjtuxb202001004. [26] WANG Jiangbin, LIU Ling, LIU Chongxin, et al. Chaos control in six-dimensional power system via adaptive synergetic approach[J]. Journal of Vibration and Control, 2020, 26(9/10): 790–800. doi: 10.1177/1077546319889850. [27] 李小腾, 王江彬, 刘崇新, 等. 四阶混沌电力系统的全局快速滑模控制器设计[J]. 科学技术与工程, 2021, 21(24): 10298–10303. doi: 10.3969/j.issn.1671-1815.2021.24.027.LI Xiaoteng, WANG Jiangbin, LIU Chongxin, et al. Global fast sliding mode controller design for a four-dimensional chaotic power system[J]. Science Technology and Engineering, 2021, 21(24): 10298–10303. doi: 10.3969/j.issn.1671-1815.2021.24.027. [28] WANG Jiangbin, LIU Ling, LIU Chongxin, et al. Fixed-time synergetic control for a seven-dimensional chaotic power system model[J]. International Journal of Bifurcation and Chaos, 2019, 29(10): 1950130. doi: 10.1142/s021812741950130x. [29] FANG Jiakun, YAO Wei, CHEN Zhe, et al. Design of anti-windup compensator for energy storage-based damping controller to enhance power system stability[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1175–1185. doi: 10.1109/tpwrs.2013.2291378. -





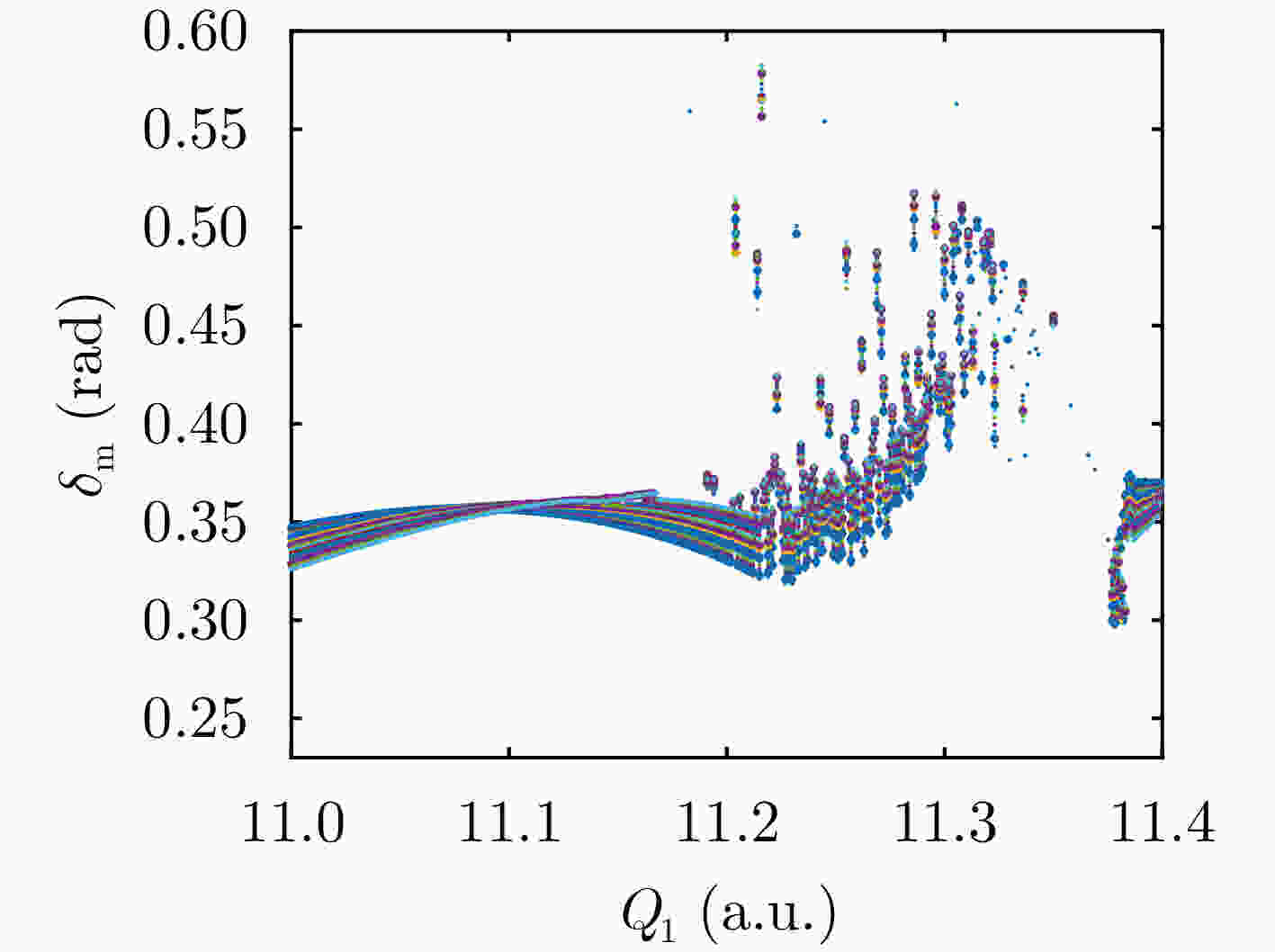
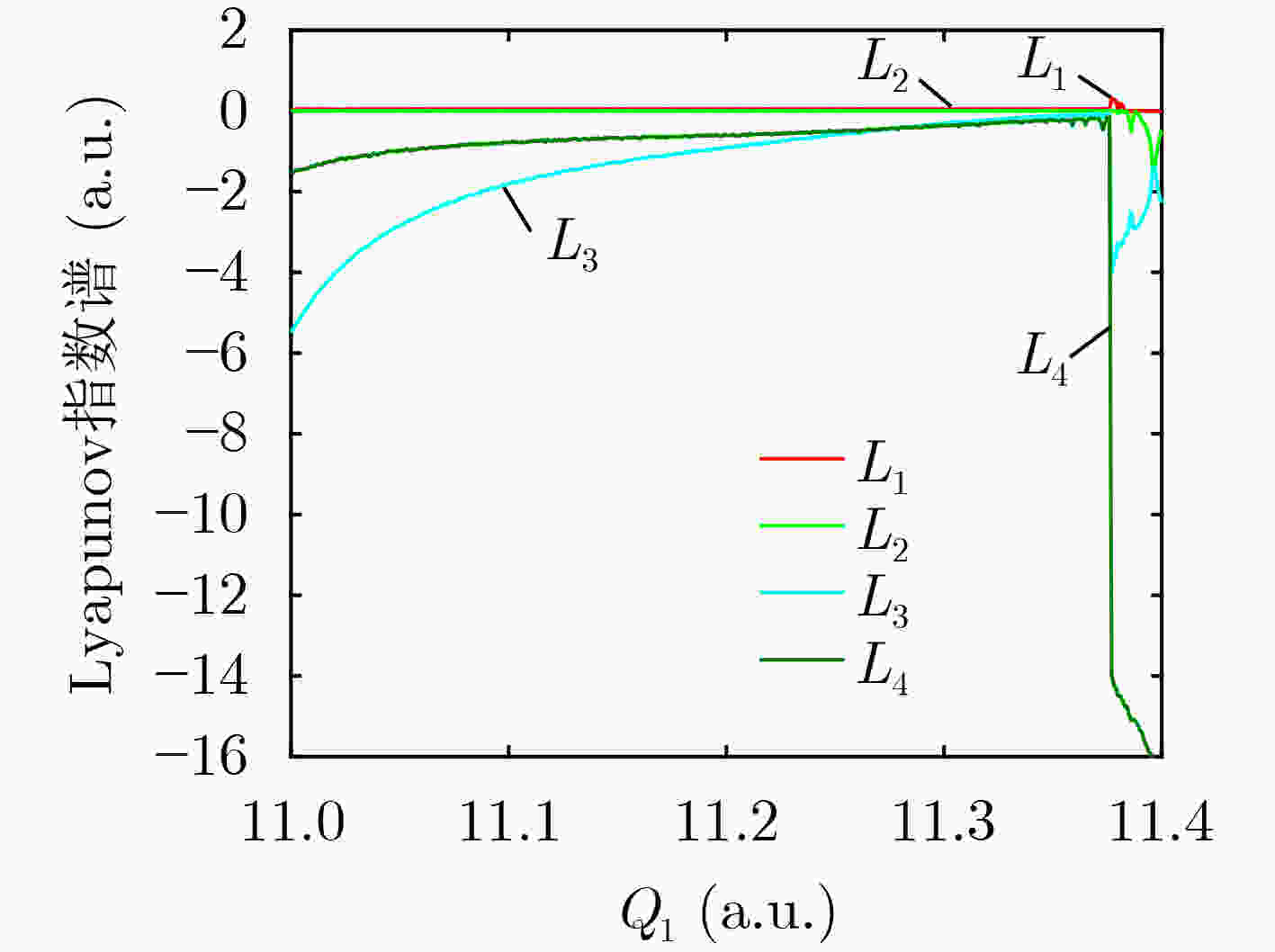
 下载:
下载:
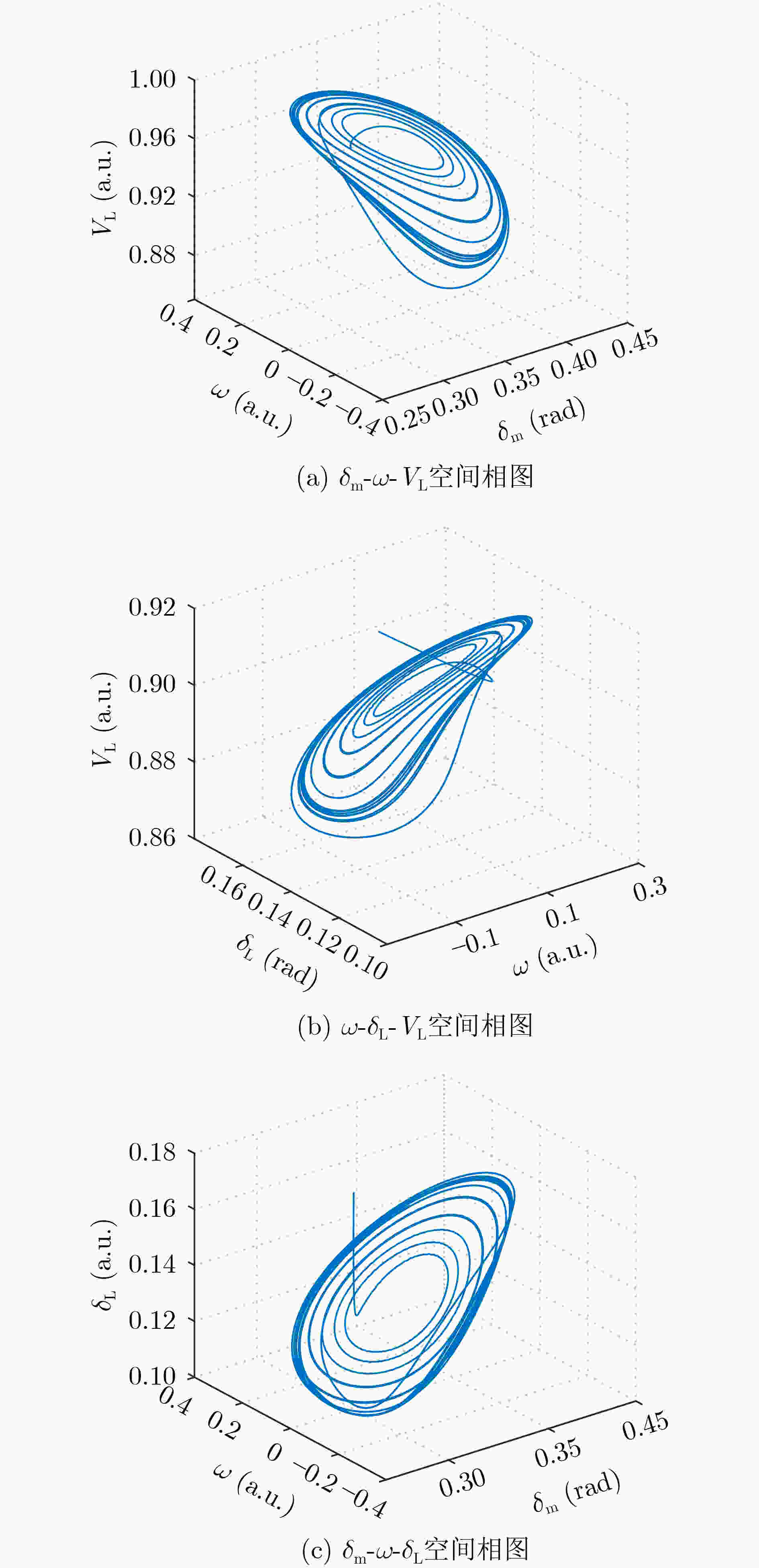
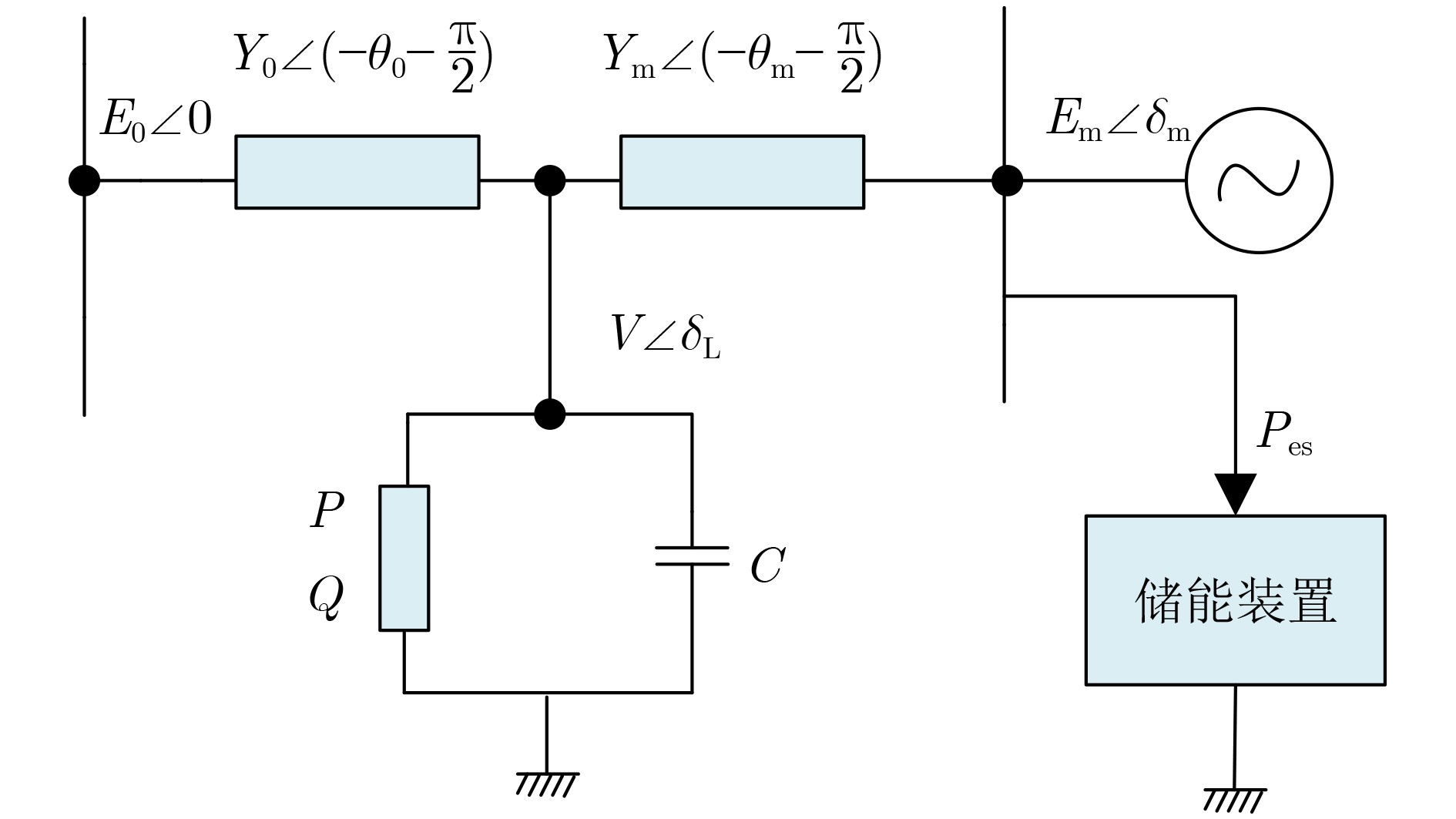
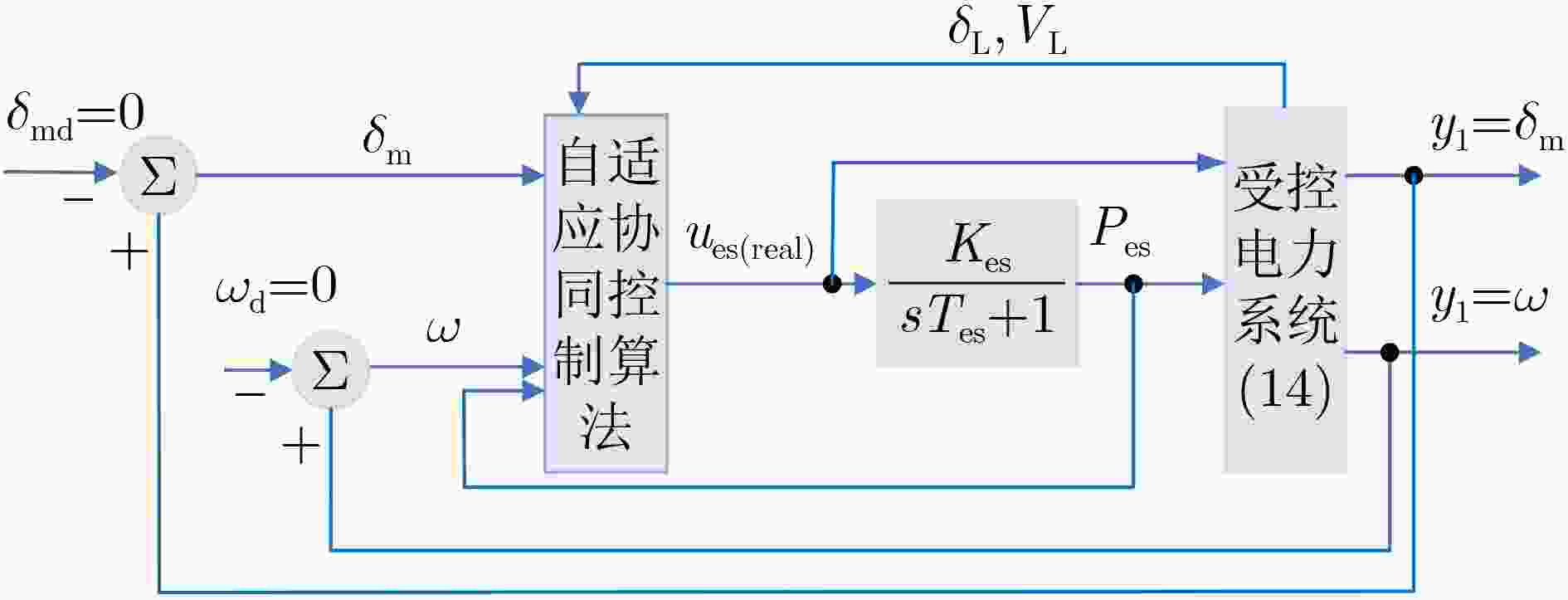
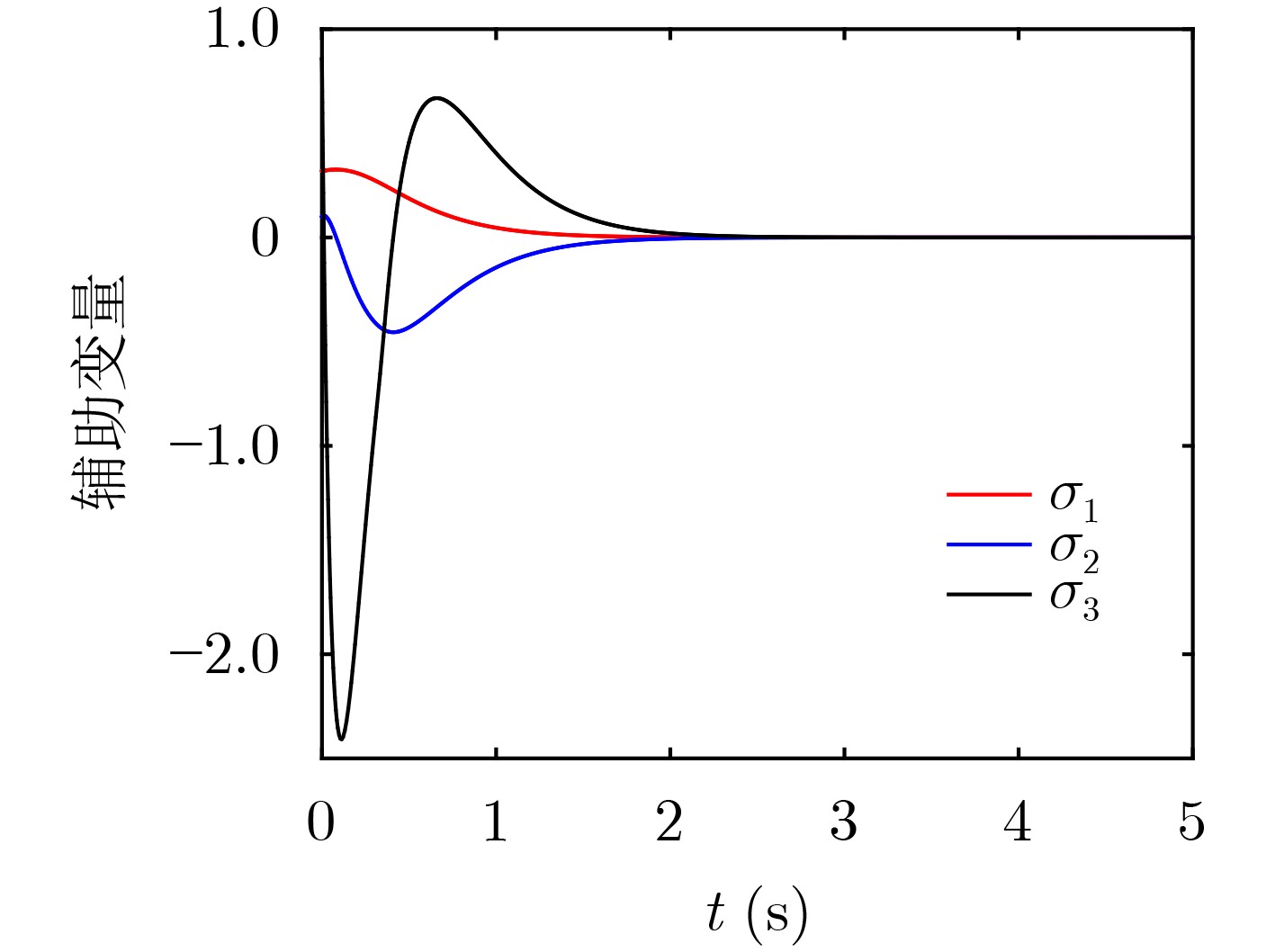
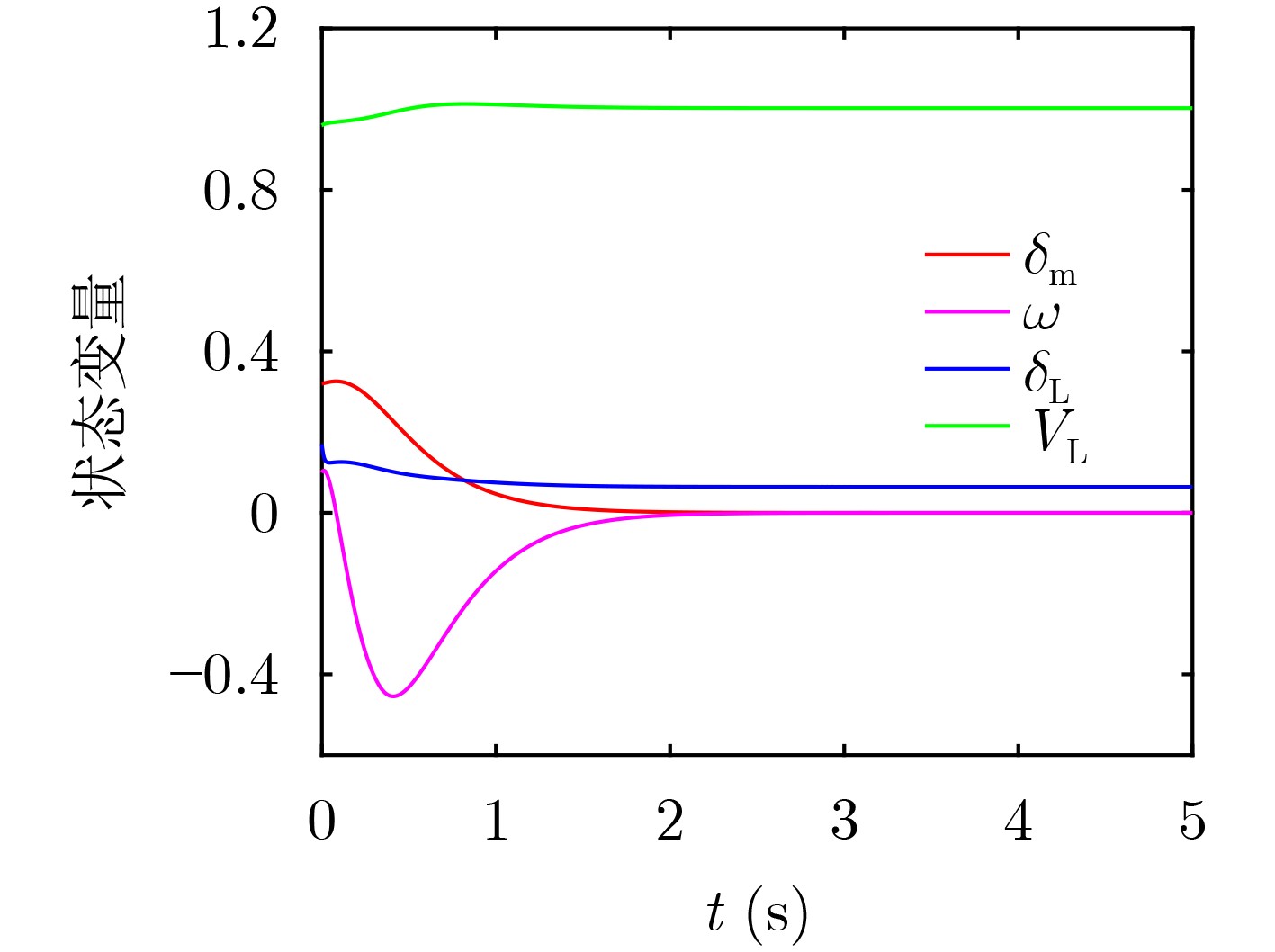
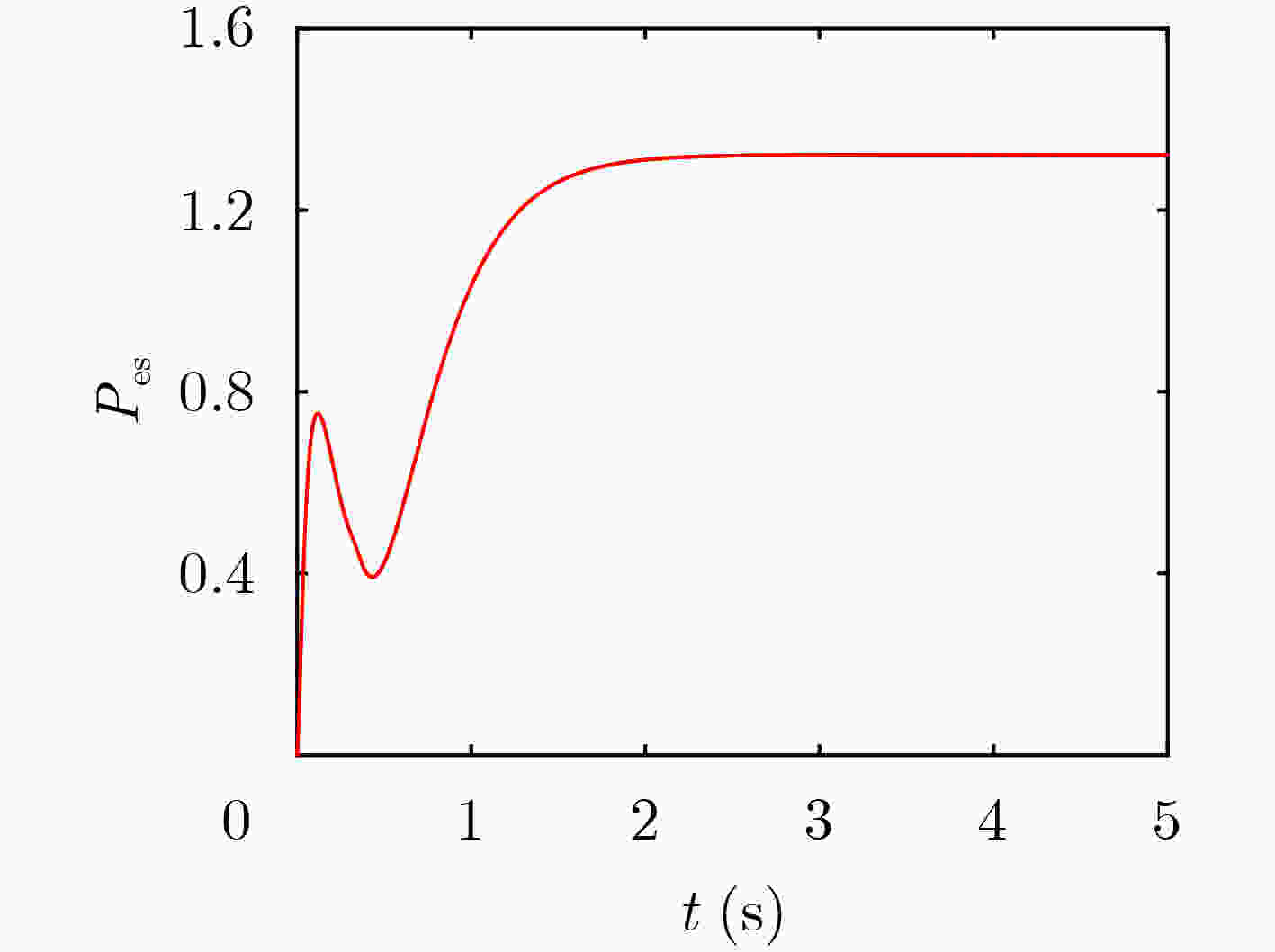
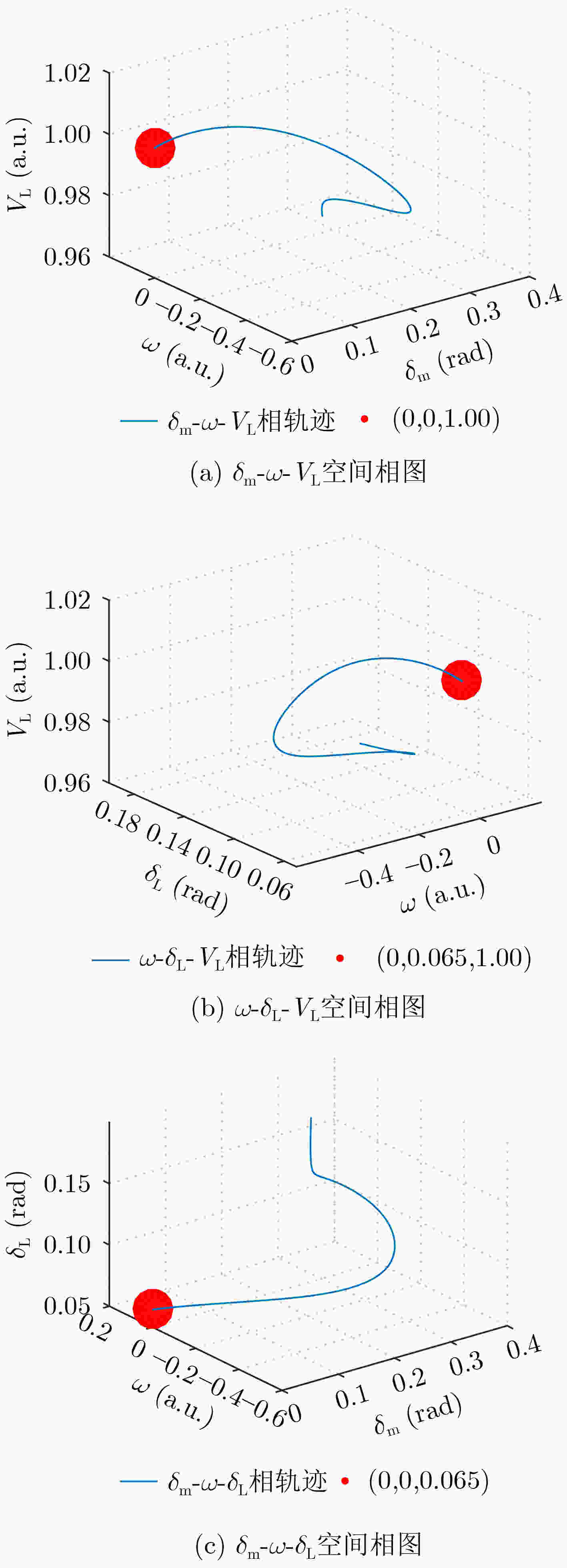
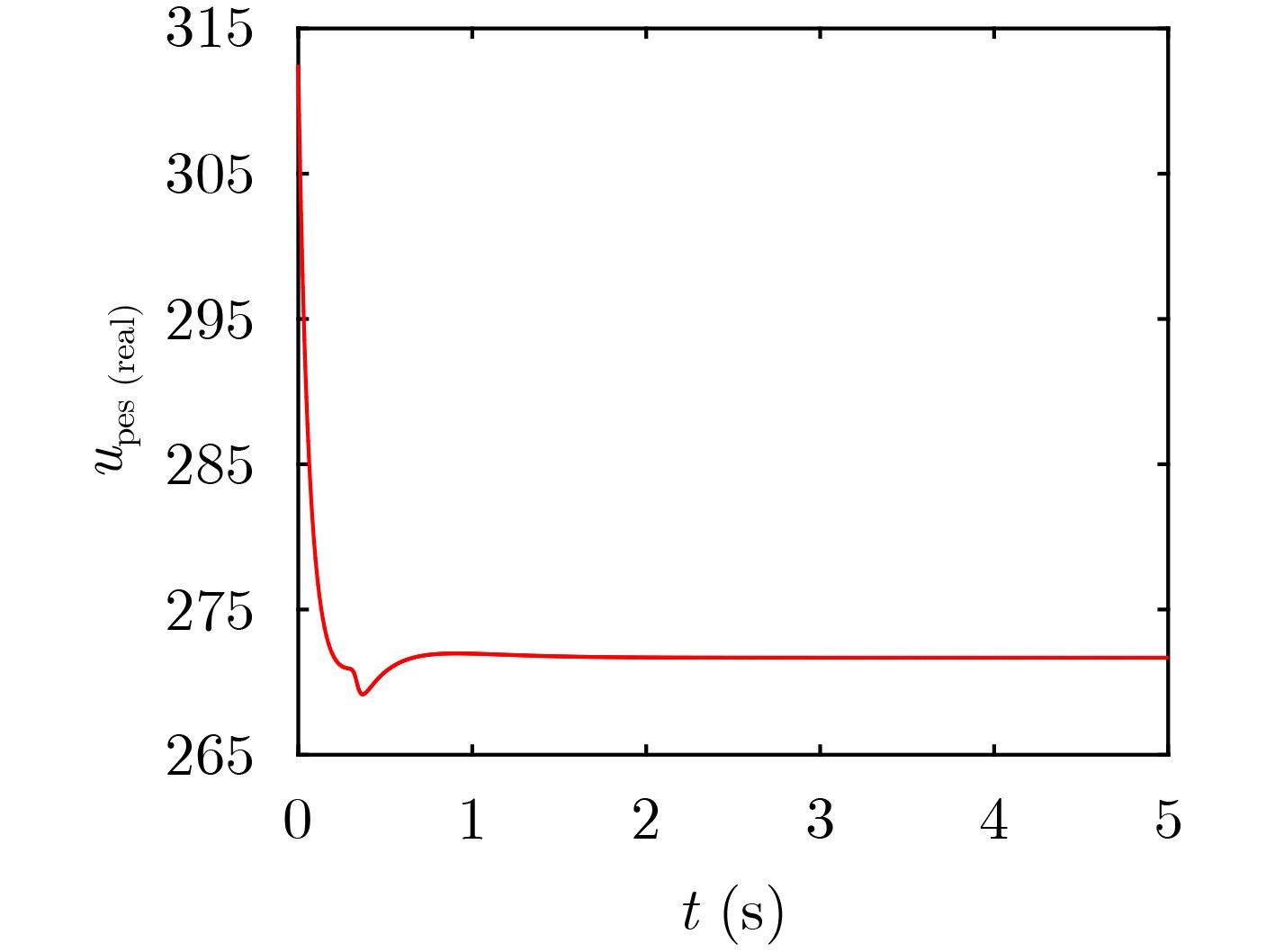
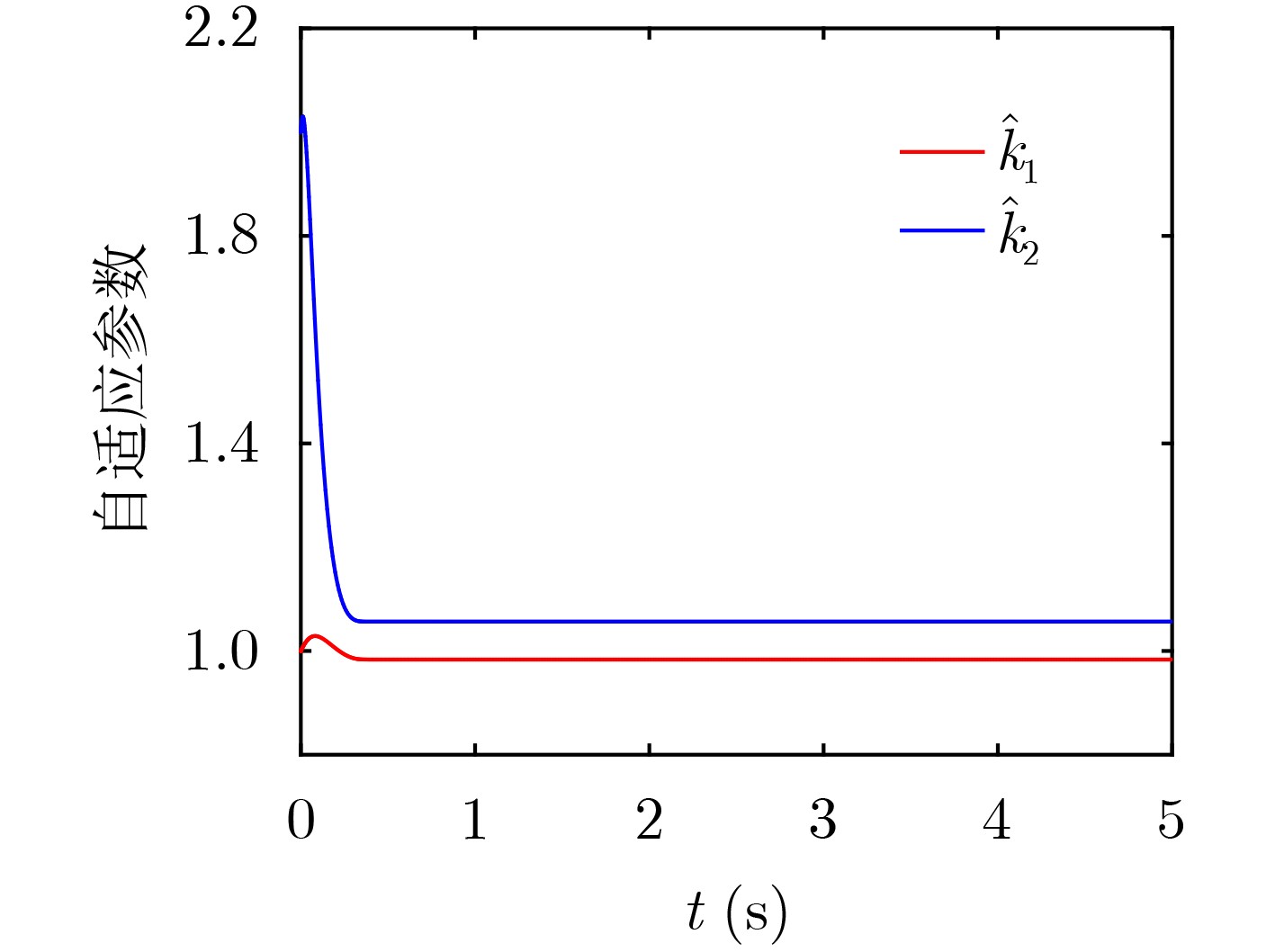


 下载:
下载:
