Estimation of Underwater Acoustic Doppler Factor and time Delay based on time-frequency Analysis of multi-component LFM Signals
-
摘要: 在水声多普勒因子和时延估计研究实用化的进程中,利用多分量线性调频(LFM)信号实现估计的算法研究越来越普遍。针对多分量LFM信号时频域存有交叉项时各分量参数估计不准确的问题,提出基于非完全残差与脊线段匹配的自适应模态分解方法。该方法采用非完全残差函数保留了交叉点处的部分时频信息,利用脊线段匹配方法提供更精确的预设时频脊线,改进了各分量LFM信号调频斜率和起始频率的估计精度。联合两个估计量进一步给出了多普勒因子和时延估计的算法。仿真结果表示,较现有模态分解算法,所提改进方法有效解决了估计分量过程中交叉区间断裂带来的估计误差;水声多径的条件下,该方法的多普勒因子和时延估计精度优于对比的现有方法。Abstract: The use of the multicomponent Linear Frequency Modulated (LFM) signals for estimating the underwater acoustic Doppler factor and time delay estimation is increasingly common in the practical process. An adaptive chirp-mode-decomposition algorithm based on incomplete residual and ridge segment matching is proposed to solve the problem of inaccurate parameter estimation for multicomponent LFM with cross-terms in the time–frequency domain. The incomplete residual function is used to retain part of the time-frequency information at the intersection point, and the ridge segment matching method is used to provide a more accurate time-frequency ridge, improving the estimation accuracy of the frequency modulation slope and starting frequency of each component of LFM signal. A combination of these two estimators provides the algorithm for estimating the Doppler factor and time delay. The results showed the proposed method effectively solves the estimation error induced by the break of cross-interval, compared with the existing mode-decomposition algorithms. The accuracy of the proposed method for estimating the Doppler factor and time delay is better than that of the existing methods in underwater acoustic multipath propagation.
-
表 1 IRSM-ACMD时频方法步骤
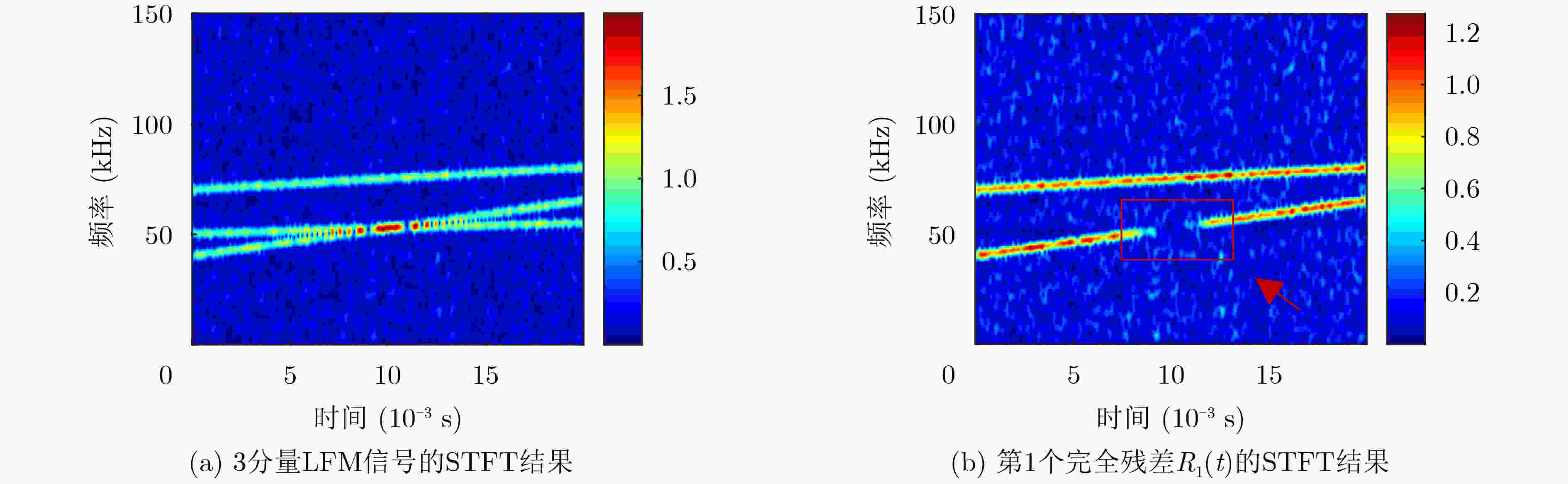
步骤1:获取一个预分量。提取第1个分量时将X(t)赋值给非完全残差IR(t),提取第m个分量时依式(5)获取非完全残差IR(t),对IR(t)进行
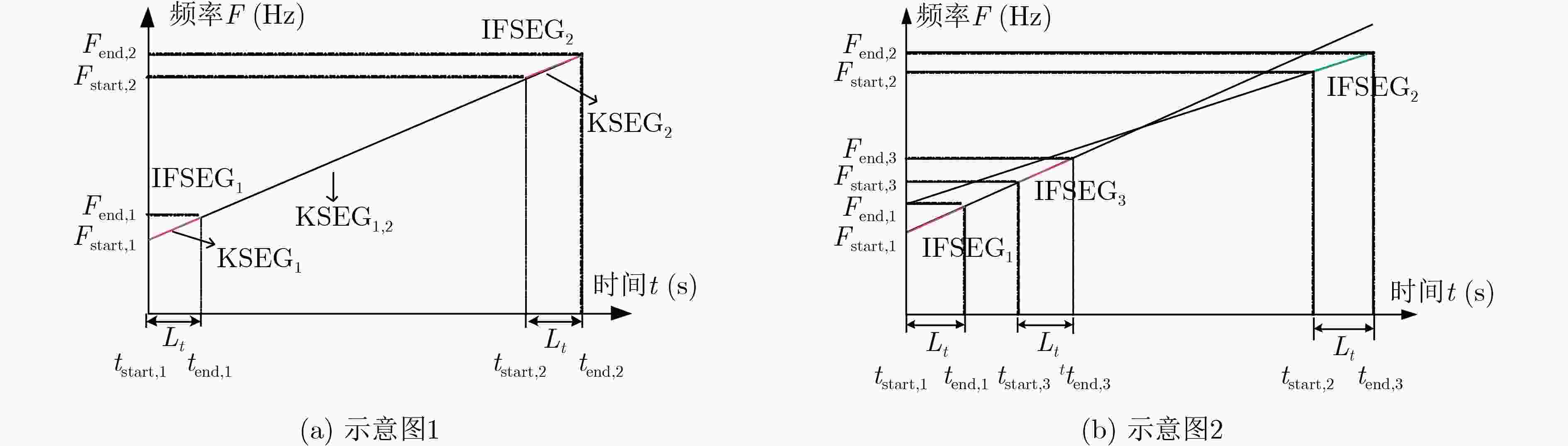
STFT得到时频分布TF(t,f),基于最大能量片段的寻找,利用式(12)—式(14)进行片段匹配后从TF(t,f)中获得其中1个分量的初始瞬时频率
即预分量。步骤2:模态分解。根据预分量及非完全残差IR(t),利用式(3)—式(4)估计出一个分量$\tilde{x}_{{w} }(t)$和它的瞬时频率$ {\tilde{F}}_{m}\left(t\right) $、瞬时幅度$ {\tilde{A}}_{m}\left(t\right) $。
并用最小二乘法拟合瞬时频率值,按式(8)更新IR(t)。步骤3:判断与循环。由式(6)判断所估计时频脊线是否重复,不重复的估计按式(7)更新到IRth(t)中,否则返回步骤1。由式(9)计算已提取
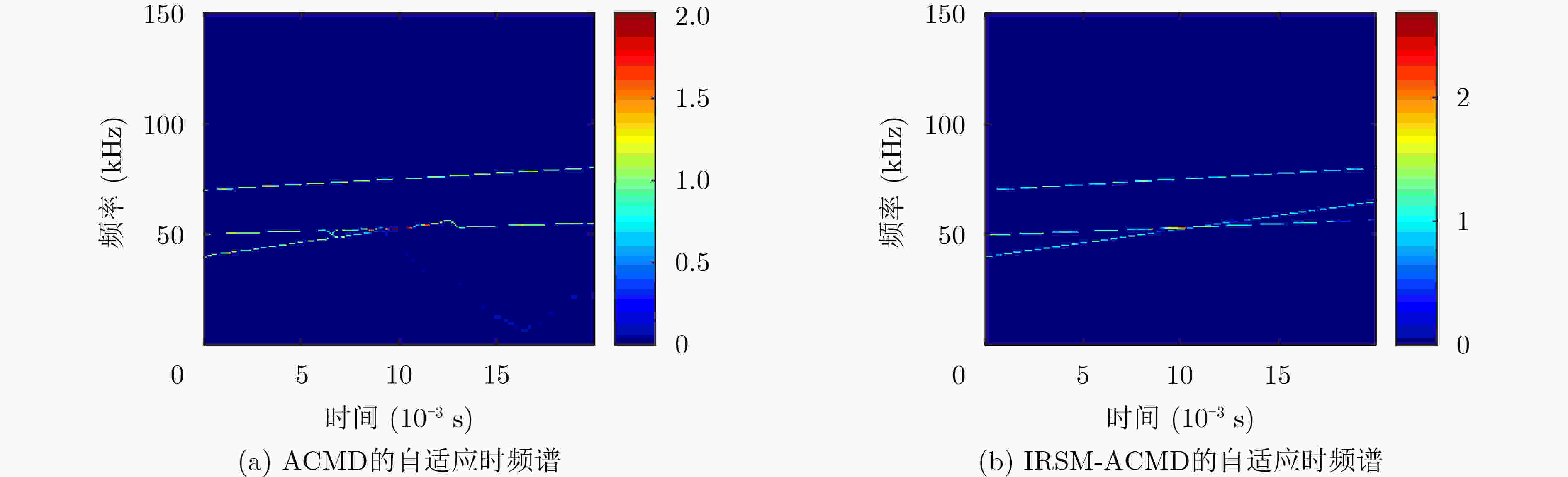
分量信号的总能量,随后由式(10)判断估计是否结束,未结束返回步骤1继续估计,若结束则由式(11)获得分量估计的自适应时频谱。表 2 发送信号为单分量LFM信号时多径信道对应的时延和多普勒因子仿真参数
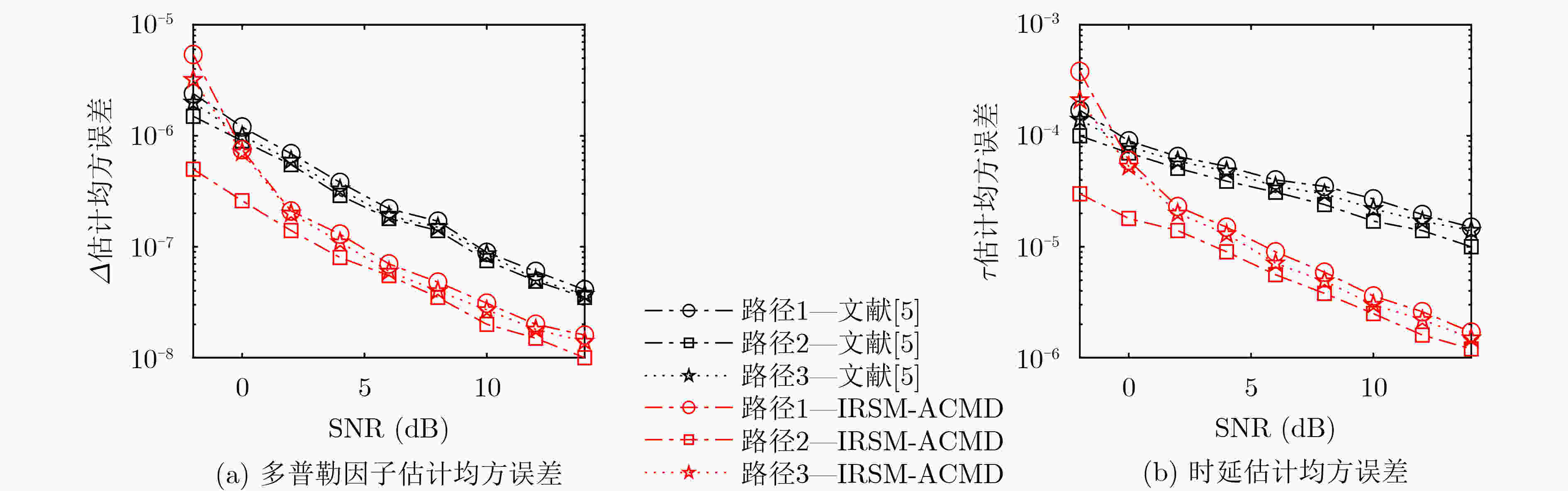
路径 时延(s) 多普勒因子 路径1(L1) 0.4562 –0.0898 路径2(L2) 0.123 0.028 路径3(L3) 3.6656 0.0898 表 3 发送信号为时频域有交叉多分量LFM信号时的仿真参数
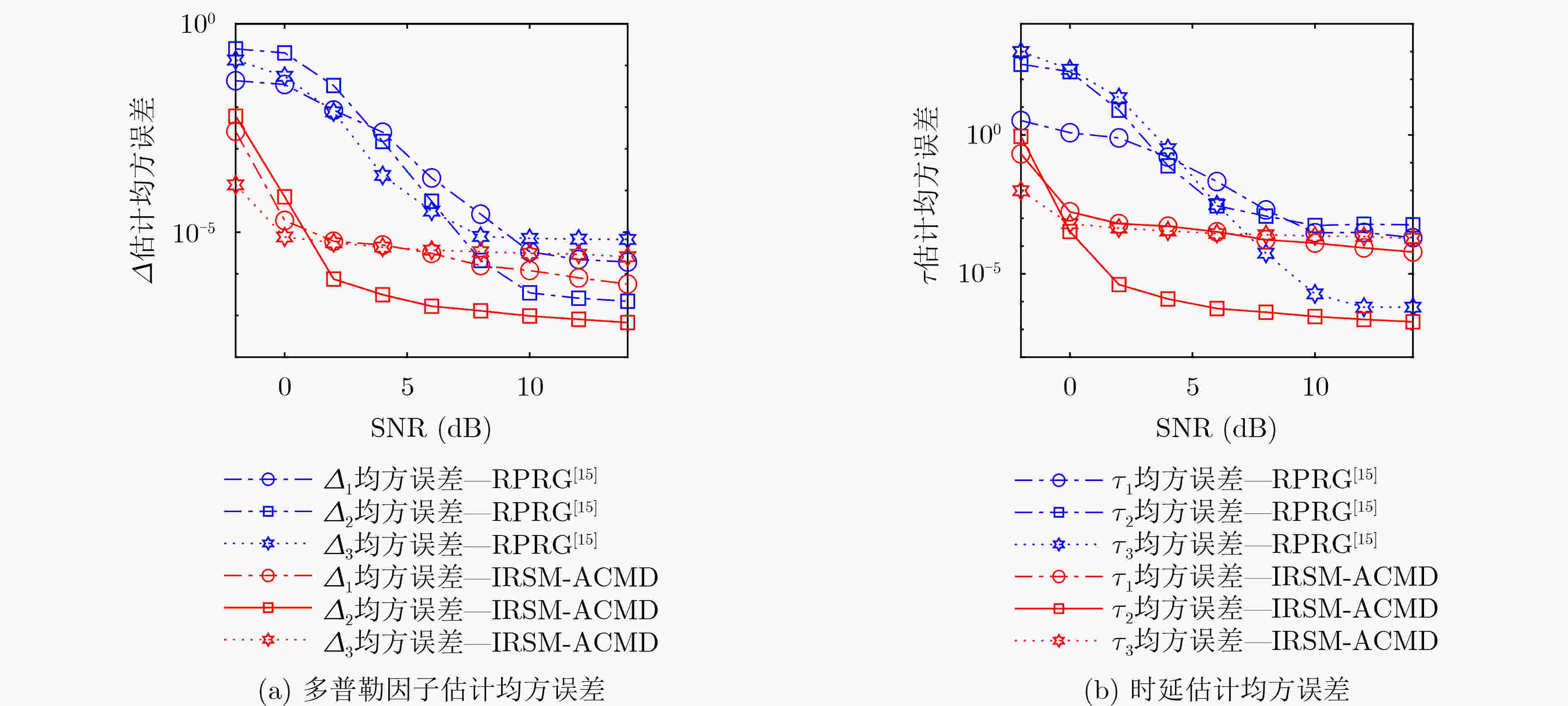
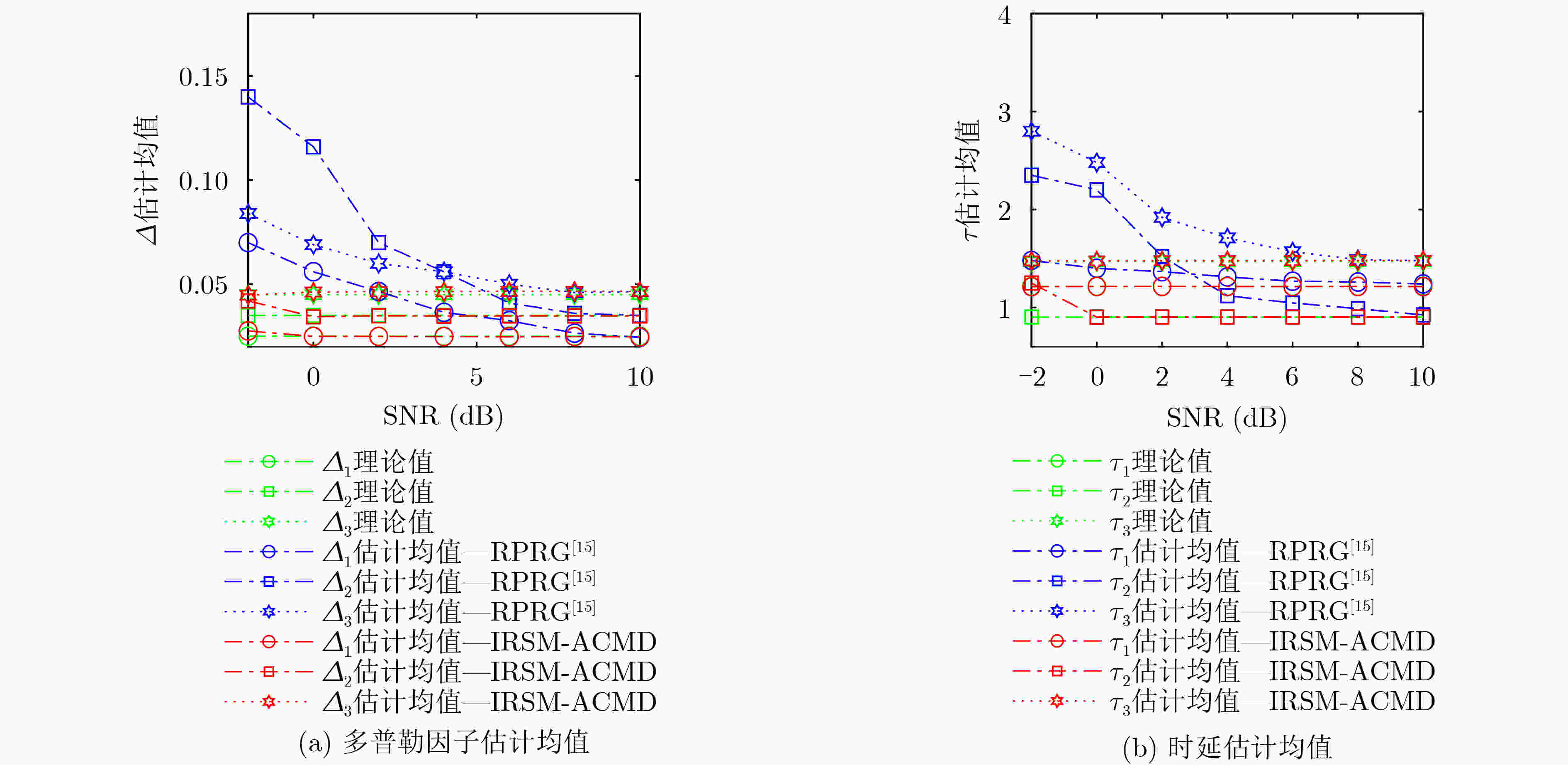
仿真参数 分量1 分量2 分量3 调频斜率(kHz/s) 1.17 3.7 1.7 起始频率(kHz) 40 35 45 截止频率(kHz) 47 57 55 多普勒因子 0.025 0.035 0.045 时延(s) 1.216 2 0.902 6 1.465 6 表 4 低频段时频域有交叉多分量LFM信号的仿真参数
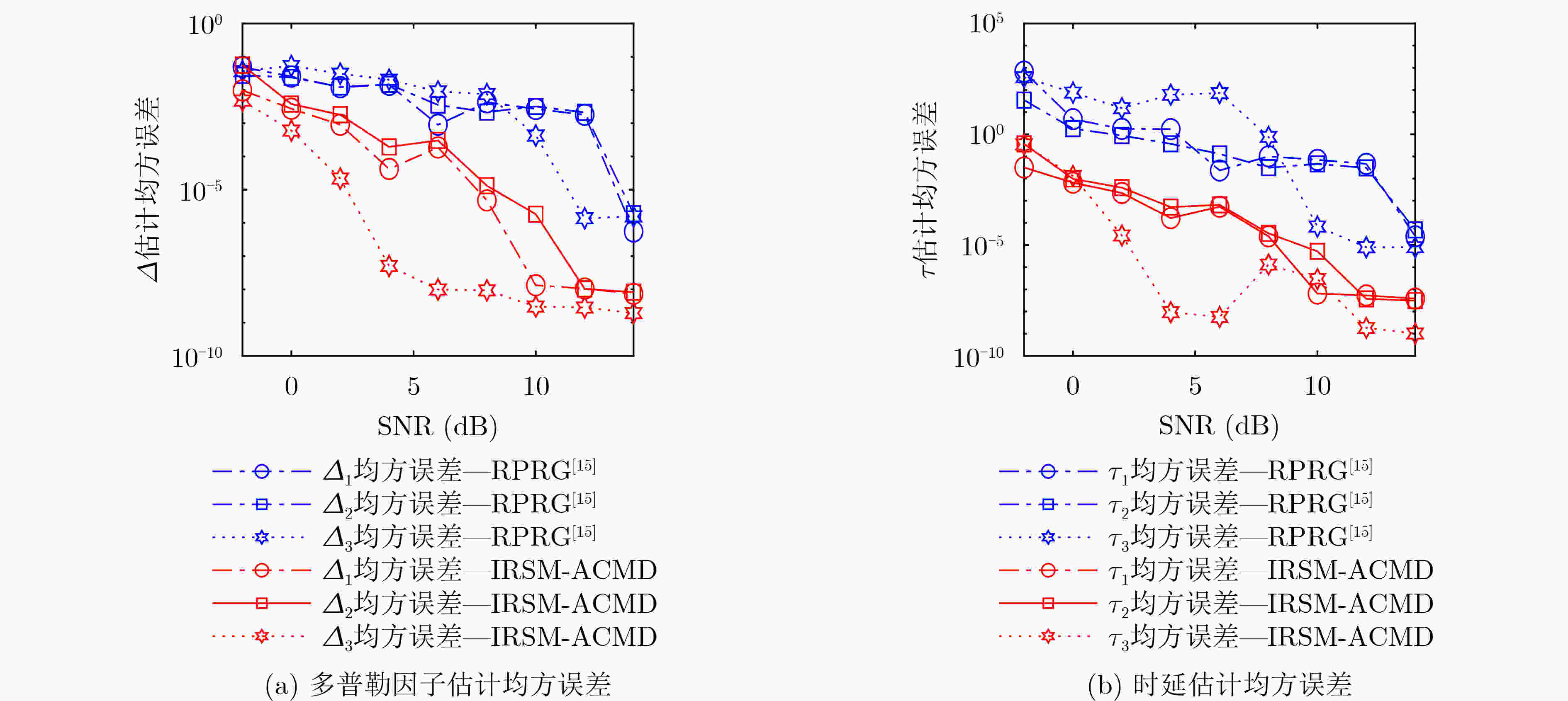
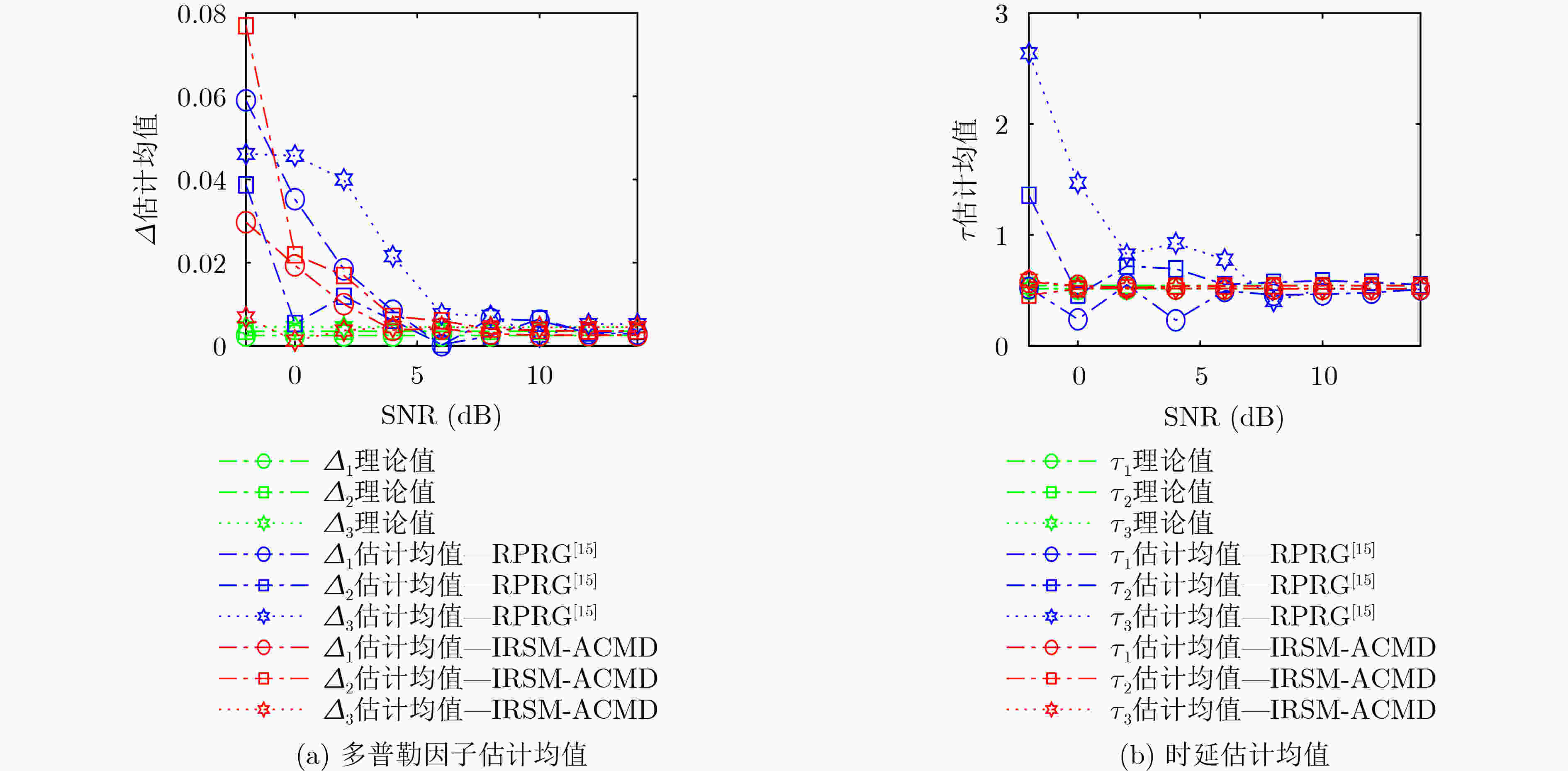
仿真参数 分量1 分量2 分量3 调频斜率(Hz/s) 800 –700 1200 起始频率(Hz) 1700 1400 800 截止频率(Hz) 2500 700 2000 多普勒因子 0.0025 0.0035 0.0045 时延(s) 0.514 3 0.543 2 0.516 6 -
[1] ZHENG Yuan, YANG Gang, and GUO Qichao. Simulation of underwater broadband noise signals’ Doppler frequency shift[C]. Proceedings of the 16th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 2022: 549–552. [2] YOO K B and EDELMANN G F. Low complexity multipath and Doppler compensation for direct-sequence spread spectrum signals in underwater acoustic communication[J]. Applied Acoustics, 2021, 180: 108094. doi: 10.1016/j.apacoust.2021.108094. [3] JOHNSON M, FREITAG L, and STOJANOVIC M. Improved Doppler tracking and correction for underwater acoustic communications[C]. Proceedings of 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 1997: 575–578. [4] SHARIF B S, NEASHAM J, HINTON O R, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2000, 25(1): 52–61. doi: 10.1109/48.820736. [5] HUANG Shuxia, FANG Shiliang, and HAN Ning. Iterative matching-based parameter estimation for time-scale underwater acoustic multipath echo[J]. Applied Acoustics, 2020, 159: 107094. doi: 10.1016/j.apacoust.2019.107094. [6] PISARENKO V F. The retrieval of harmonics from a covariance function[J]. Geophysical Journal of the Royal Astronomical Society, 1973, 33(3): 347–366. doi: 10.1111/j.1365-246X.1973.tb03424.x. [7] YANG Jie, LIU Xiangtian, and YU Fengqi. Doppler shift estimation algorithm with low computational complexity for underwater acoustic communication[C]. Proceedings of the IEEE 16th International Conference on Communication Technology (ICCT), Hangzhou, China, 2015: 47–50. [8] ZHAO Yanbo, YU Hua, WEI Gang, et al. Parameter estimation of wideband underwater acoustic multipath channels based on fractional fourier transform[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5396–5408. doi: 10.1109/tsp.2016.2582466. [9] ZHU Yijia, ZHANG Lanyue, and MA Jiaxin. Modeling and estimation of the space-time varying channels[C]. Proceedings of 2021 OES China Ocean Acoustics, Harbin, China, 2021: 758–762. [10] SU Yishan, LIU Xuan, JIN Zhigang, et al. Fast estimation of underwater acoustic multipath channel based on LFM signal[C]. Global Oceans 2020: Singapore – U. S. Gulf Coast, Biloxi, USA, 2020: 1–5. [11] 李家强, 金荣洪, 耿军平, 等. 基于高斯短时分数阶傅里叶变换的多分量LFM信号检测与参数估计[J]. 电子与信息学报, 2007, 29(3): 570–573. doi: 10.3724/SP.J.1146.2005.00857.LI Jiaqiang, JIN Ronghong, GENG Junping, et al. Detection and estimation of multi-component LFM signals based on gauss short-time fractional Fourier transform[J]. Journal of Electronics &Information Technology, 2007, 29(3): 570–573. doi: 10.3724/SP.J.1146.2005.00857. [12] 金艳, 段鹏婷, 姬红兵. 复杂噪声环境下基于LVD的LFM信号参数估计[J]. 电子与信息学报, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013.JIN Yan, DUAN Pengting, and JI Hongbing. Parameter estimation of LFM signals based on LVD in complicated noise environments[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013. [13] CHEN Shiqian, DONG Xingjian, PENG Zhike, et al. Nonlinear chirp mode decomposition: A variational method[J]. IEEE Transactions on Signal Processing, 2017, 65(22): 6024–6037. doi: 10.1109/tsp.2017.2731300. [14] CHEN Shiqian, YANG Yang, PENG Zhike, et al. Detection of rub-impact fault for rotor-stator systems: A novel method based on adaptive chirp mode decomposition[J]. Journal of Sound and Vibration, 2019, 440: 83–99. doi: 10.1016/j.jsv.2018.10.010. [15] 赵雅琴, 聂雨亭, 吴龙文, 等. 基于脊路跟踪的变分非线性调频模态分解方法[J]. 浙江大学学报: 工学版, 2020, 54(10): 1874–1882.ZHAO Yaqin, NIE Yuting, WU Longwen, et al. Multi-component signal separation using variational nonlinear chirp mode decomposition based on ridge tracking[J] Journal of Zhejiang University: Engineering Science, 2020, 54(10): 1874–1882. [16] MEIGNEN S, PHAM D H, and MCLAUGHLIN S. On demodulation, ridge detection, and synchrosqueezing for multicomponent signals[J]. IEEE Transactions on Signal Processing, 2017, 65(8): 2093–2103. doi: 10.1109/TSP.2017.2656838. [17] ZHOU Yuehai, TONG Feng, SONG Aijun, et al. Exploiting spatial–temporal joint sparsity for underwater acoustic Multiple-Input–Multiple-Output communications[J]. IEEE Journal of Oceanic Engineering, 2021, 46(1): 352–369. doi: 10.1109/JOE.2019.2958003. -





 下载:
下载:


 下载:
下载:
