An Optimization Method for Transmitting Waveform of Polarimetric Radar Against Interrupted Sampling Repeater Jamming
-
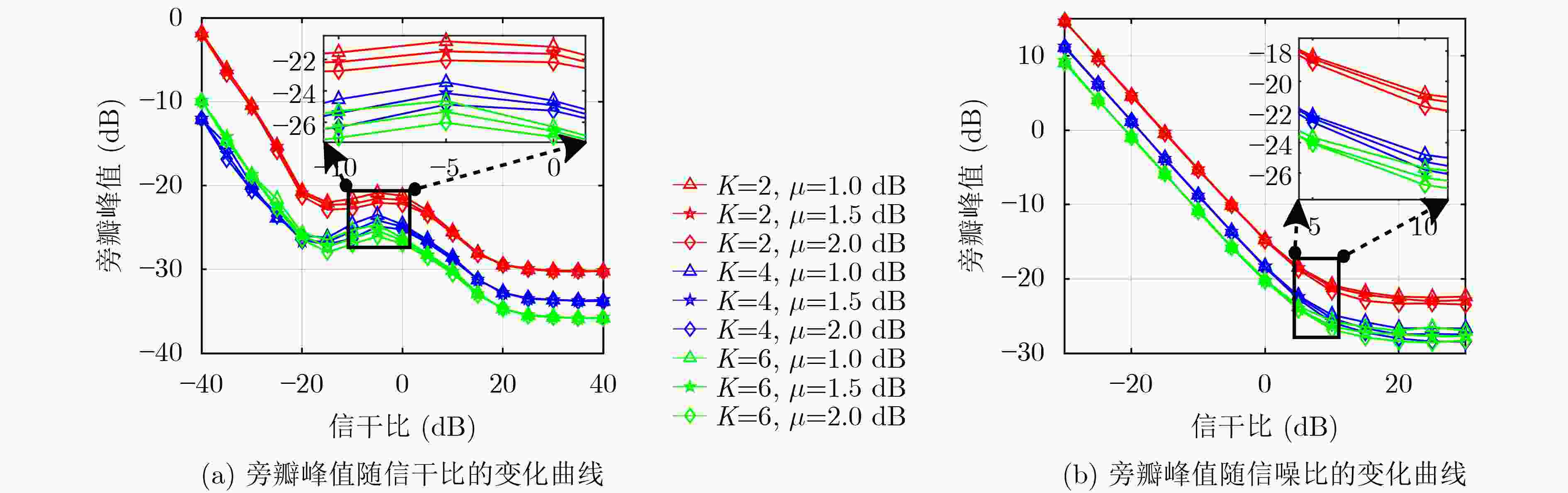
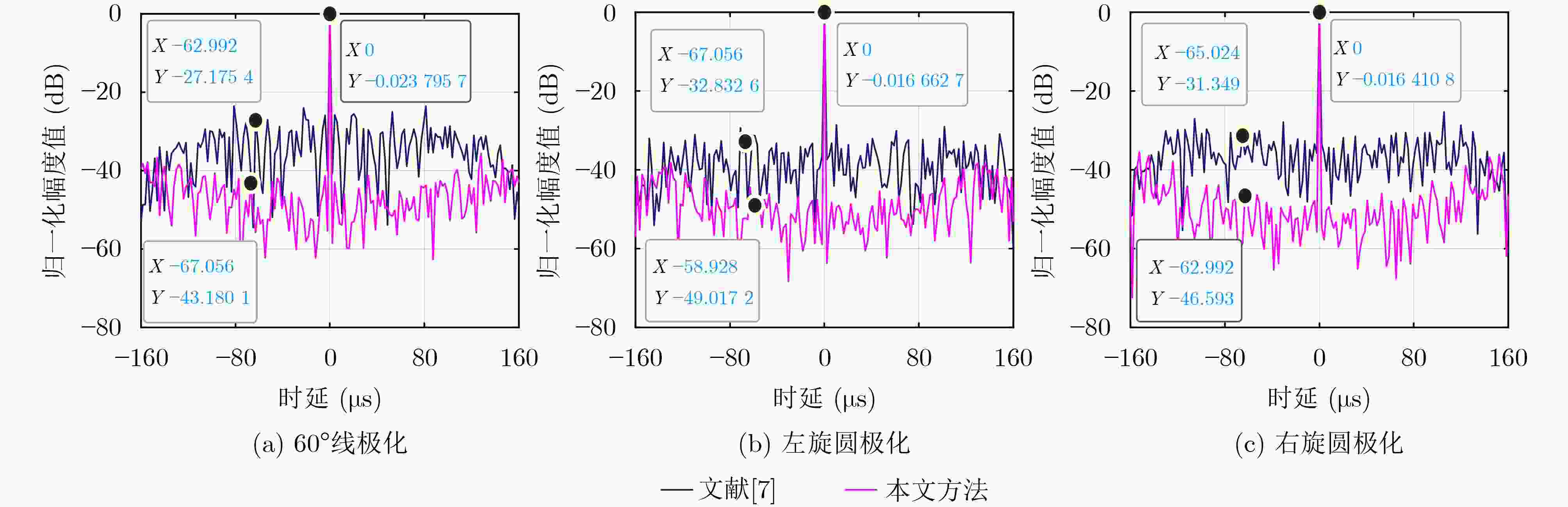
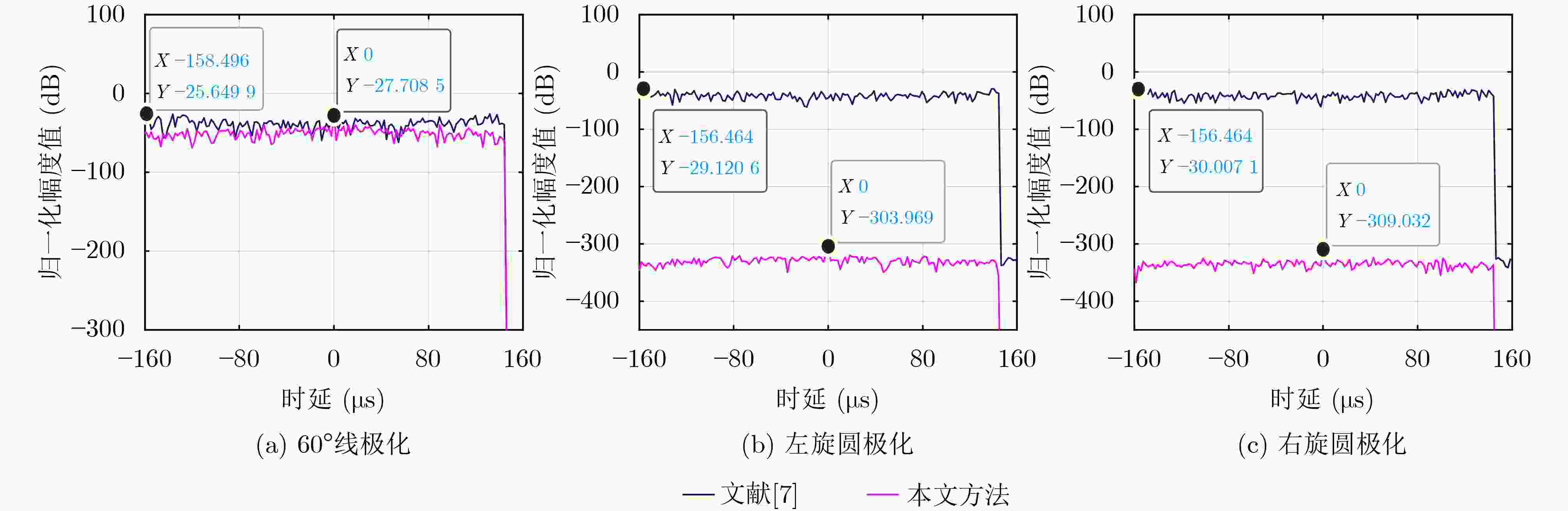
摘要: 作为一种新型的有源干扰样式,间歇采样转发干扰(ISRJ)引起了人们越来越多的关注。极化是表征电磁波矢量性的重要参数,其引入可以显著提高雷达在抗干扰方面的性能。为此,该文针对性地研究了全极化雷达的抗ISRJ方法,通过波形设计和优化以获取比传统单极化雷达更好的抗干扰性能。另外,针对宽带雷达条件下现有抗ISRJ问题表征中未考虑目标特性对信号调制作用这一短板,该文在信干比的数学表达式中加入了目标特性调制这一因素。在此基础上,提出了一种具有多普勒容忍的抗ISRJ全极化雷达波形设计方法。采用实测目标数据开展的实验表明:与单极化雷达相比,极化信息的引入显著提高了雷达对ISRJ的抑制性能;宽带条件下,考虑扩展目标对信号的调制作用在信干比的计算上具有必要性。Abstract: Interrupted Sampling Repeater Jamming (ISRJ) has attracted increasing attention as a new type of active jamming. Polarization is an important parameter for characterizing an electromagnetic wave vector and can substantially improve radar anti-jamming performance. Therefore, in this study, the anti-ISRJ method of polarimetric radar is studied. Here, better anti-jamming performance than that of traditional radar is obtained through waveform design and optimization. Additionally, because the modulation effect of target characteristics on a signal is neglected in the existing characterization of the anti-ISRJ problem under wideband radar conditions, this paper includes target characteristics factors to the mathematical expression of SJR. Finally, on this basis, a waveform design method of anti-ISRJ polarimetric radar with Doppler tolerance is proposed. Experiments using the measured target data show that compared with traditional radar, the introduction of polarization information improves substantially radar ISRJ suppression performance; moreover, under wideband conditions, the modulation effect of the extended target on the signal must be considered when calculating SJR.
-
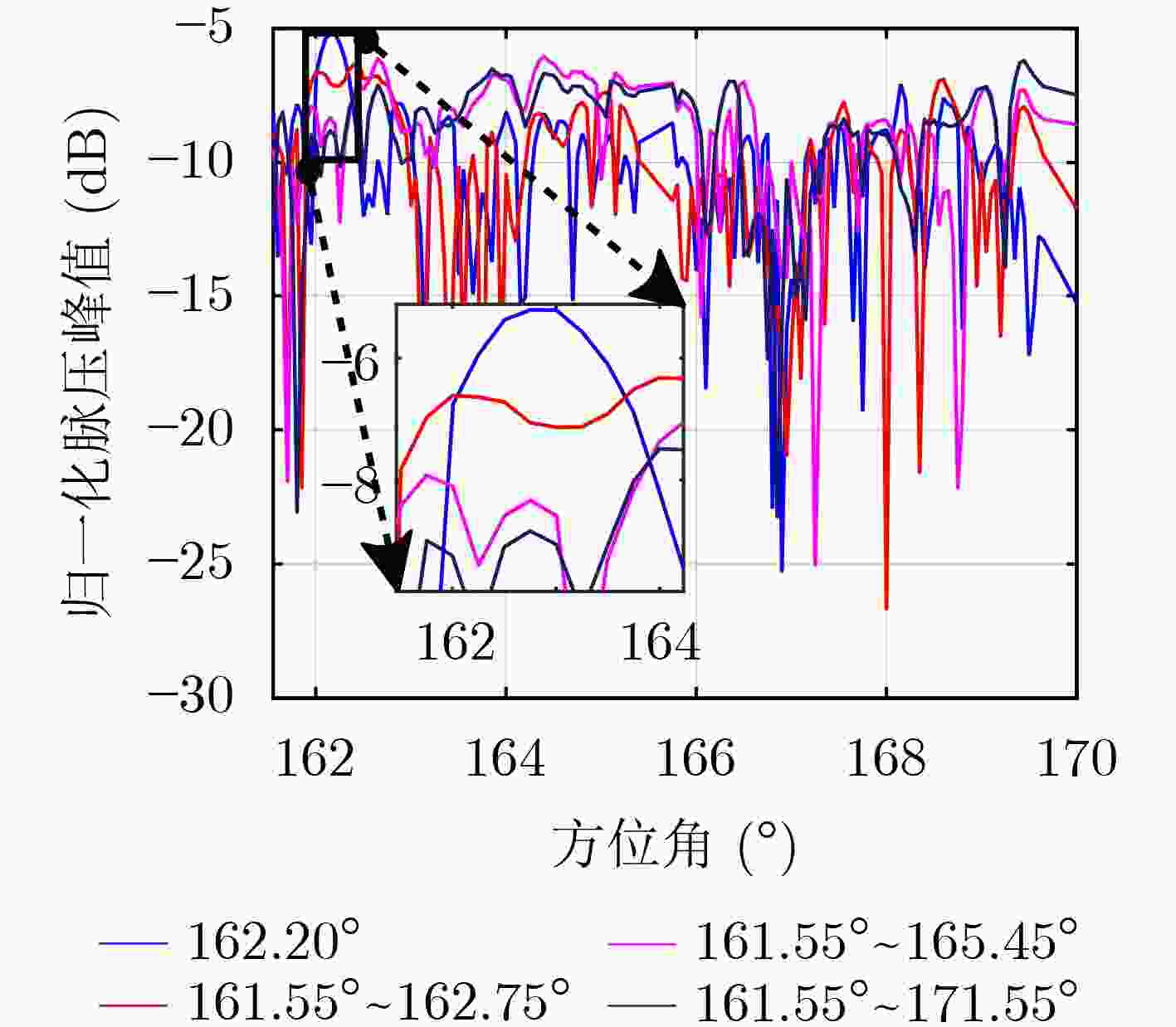
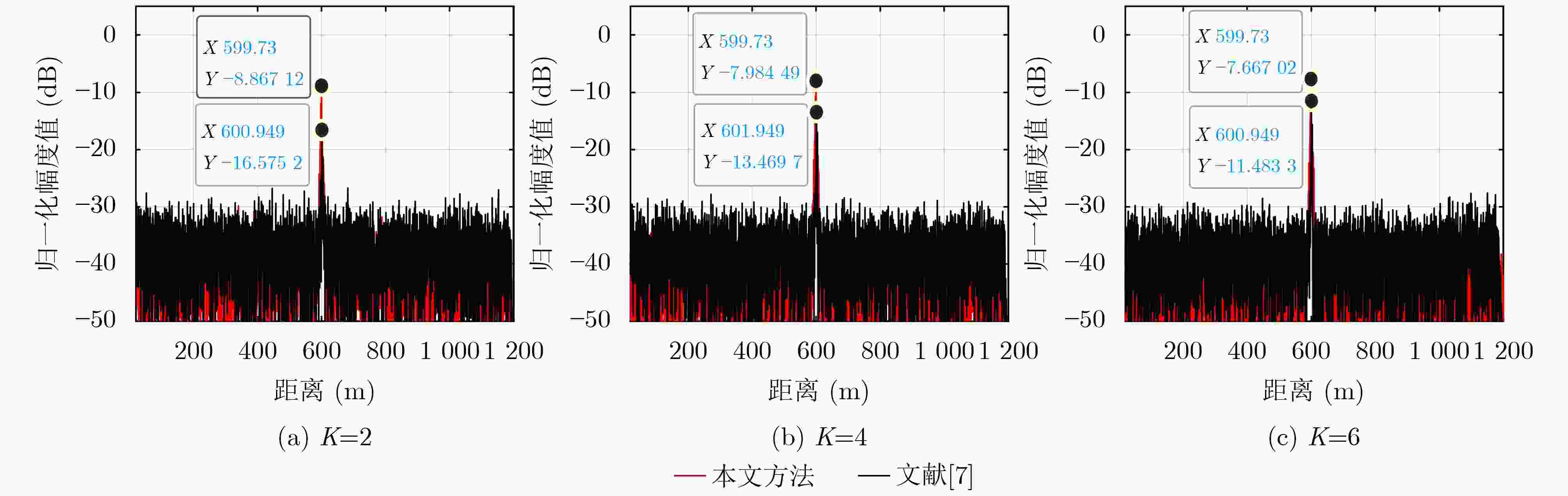
图 8 不同脉冲数条件下本文方法与文献[7]方法的脉压结果对比
算法1 宽带全极化雷达抗ISRJ恒模互补波形设计流程 输入:目标脉冲响应矩阵$\overline {{\boldsymbol{H}}(\theta )}$、干扰特性矩阵${\boldsymbol{C}}$、初始${\boldsymbol{s}}$,${\boldsymbol{w}}$和
${\boldsymbol{\varepsilon}} $输出:最优发射波形序列${{\boldsymbol{s}}^\nabla }$、接收滤波器序列${{\boldsymbol{w}}^\nabla }$和Jones矢量${{\boldsymbol{\varepsilon}} ^\nabla }$ 1 重复 2 将${{\boldsymbol{w}}^{(i)} }$代入式(31)计算${{\boldsymbol{w}}_1}$,将${{\boldsymbol{w}}_1}$代入式(31)计算${{\boldsymbol{w}}_2}$ 3 ${{\boldsymbol{r}}_1} = {{\boldsymbol{w}}_1} - {{\boldsymbol{w}}^{(i)} }$, ${{\boldsymbol{v}}_1} = {{\boldsymbol{w}}_2} - {{\boldsymbol{w}}_1} - {{\boldsymbol{r}}_1}$$ , $ ${\alpha _1} = - {{\boldsymbol{r}}_1}/{{\boldsymbol{v}}_1}$ 4 将${ {\boldsymbol{w} }^{(i)} } - 2{\alpha _1}{ {\boldsymbol{r} }_1} + {\alpha _1}^2{{\boldsymbol{v}}_1}$代入式(31)计算${{\boldsymbol{w}}^{(i + 1)}}$ 5 若$ \varGamma \left( {{{\boldsymbol{s}}^{{\text{(}}i{\text{)}}}},{{\boldsymbol{w}}^{(i + 1)}},{{\boldsymbol{\varepsilon }}^{{\text{(}}i{\text{)}}}}} \right) > \varGamma \left( {{{\boldsymbol{s}}^{{\text{(}}i{\text{)}}}},{{\boldsymbol{w}}^{{\text{(}}i{\text{)}}}},{{\boldsymbol{\varepsilon}} ^{{\text{(}}i{\text{)}}}}} \right) $,循环 6 ${\alpha _1} \leftarrow \left( {{\alpha _1} - 1} \right)/2$ 7 将${{\boldsymbol{w}} ^{{\text{(}}i{\text{)}}}} - 2{\alpha _1}{{\boldsymbol{r}}_1} + {\alpha _1}^2{{\boldsymbol{v}}_1}$代入式(31)计算${{\boldsymbol{w}}^{{\text{(}}i + 1{\text{)}}}}$ 8 结束 9 将${{\boldsymbol{s}}^{{\text{(}}i{\text{)}}}}$代入式(38)计算${{\boldsymbol{s}}_1}$,将${{\boldsymbol{s}}_1}$代入式(38)计算${{\boldsymbol{s}}_2}$ 10 ${{\boldsymbol{r}}_2} = {{\boldsymbol{s}}_1} - {{\boldsymbol{s}}^{{\text{(}}i{\text{)}}}}$, ${{\boldsymbol{v}}_2} = {{\boldsymbol{s}}_2} - {{\boldsymbol{s}}_1} - {{\boldsymbol{r}}_1},{\text{ }}{\alpha _2} = - {{\boldsymbol{r}}_2}/{{\boldsymbol{v}}_2}$ 11 将${{\boldsymbol{s}}^{ {\text{(} }i{\text{)} } } } - 2{\alpha _2}{{\boldsymbol{r}}_2} + {\alpha _2}^2{{\boldsymbol{v}}_2}$代入式(38)计算${s^{{\text{(}}i + 1{\text{)}}}}$ 12 若$\varGamma \left( {{{\boldsymbol{s}}^{{\text{(}}i + 1{\text{)}}}},{{\boldsymbol{w}}^{{\text{(}}i + 1{\text{)}}}},{{\boldsymbol{\varepsilon}} ^{{\text{(}}i{\text{)}}}}} \right) > \varGamma \left( {{{\boldsymbol{s}}^{{\text{(}}i{\text{)}}}},{{\boldsymbol{w}}^{{\text{(}}i + 1{\text{)}}}},{{\boldsymbol{\varepsilon}} ^{{\text{(}}i{\text{)}}}}} \right)$,循环 13 ${\alpha _2} \leftarrow \left( {{\alpha _2} - 1} \right)/2$ 14 将${ {\boldsymbol{s} }^{ {\text{(} }i{\text{)} } } } - 2{\alpha _2}{{\boldsymbol{r}}_2} + {\alpha _2}^2{ {\boldsymbol{v} }_2}$代入式(38)计算${{\boldsymbol{s}}^{{\text{(}}i + 1{\text{)}}}}$ 15 结束 16 使用网格法迭代求解${{\boldsymbol{\varepsilon}} ^{{\text{(}}i + 1{\text{)}}}}$ 17 $i \leftarrow i + 1$ 18 达到收敛条件,结束 -
[1] 周超, 刘泉华, 曾涛. DRFM间歇采样转发式干扰辨识算法研究[J]. 信号处理, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002ZHOU Chao, LIU Quanhua, and ZENG Tao. Research on DRFM repeater jamming recognition[J]. Journal of Signal Processing, 2017, 33(7): 911–917. doi: 10.16798/j.issn.1003-0530.2017.07.002 [2] WEN Cai, PENG Jinye, ZHOU Yan, et al. Enhanced three-dimensional joint domain localized STAP for airborne FDA-MIMO radar under dense false-target jamming scenario[J]. IEEE Sensors Journal, 2018, 18(10): 4154–4166. doi: 10.1109/JSEN.2018.2820905 [3] SUN Qingyang, SHU Ting, YU K B, et al. A novel deceptive jamming method against two-channel SAR-GMTI based on two jammers[J]. IEEE Sensors Journal, 2019, 19(14): 5600–5610. doi: 10.1109/JSEN.2019.2908030 [4] LAN Lan, LIAO Guisheng, XU Jingwei, et al. Suppression approach to main-beam deceptive jamming in FDA-MIMO radar using nonhomogeneous sample detection[J]. IEEE Access, 2018, 6: 34582–34597. doi: 10.1109/ACCESS.2018.2850816 [5] 刘忠, 王雪松, 刘建成, 等. 基于数字射频存储器的间歇采样重复转发干扰[J]. 兵工学报, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005LIU Zhong, WANG Xuesong, LIU Jiancheng, et al. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory[J]. Acta Armamentarii, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005 [6] 周凯, 何峰, 粟毅. 一种快速抗间歇采样转发干扰波形和滤波器联合设计算法[J]. 雷达学报, 2022, 11(2): 264–277. doi: 10.12000/JR22015ZHOU Kai, HE Feng, and SU Yi. Fast algorithm for joint waveform and filter design against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 264–277. doi: 10.12000/JR22015 [7] 王福来, 庞晨, 殷加鹏, 等. 一种多普勒容忍的抗间歇采样转发干扰恒模互补波形和接收滤波器联合设计方法[J]. 雷达学报, 2022, 11(2): 278–288. doi: 10.12000/JR22020WANG Fulai, PANG Chen, YIN Jiapeng, et al. Joint design of doppler-tolerant complementary sequences and receiving filters against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 278–288. doi: 10.12000/JR22020 [8] 周畅, 汤子跃, 朱振波, 等. 抗间歇采样转发干扰的波形设计方法[J]. 电子与信息学报, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236ZHOU Chang, TANG Ziyue, ZHU Zhenbo, et al. Anti-interrupted sampling repeater jamming waveform design method[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236 [9] 张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM波形的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti interrupted-sampling repeater jamming method based on stepped LFM waveform[J]. Systems Engineering and Electronics, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12 [10] 盖季妤, 姜维, 张凯翔, 等. 基于差分特征的间歇采样转发干扰辨识与抑制方法[J]. 雷达学报, 2023, 12(1): 186–196. doi: 10.12000/JR22058GAI Jiyu, JIANG Wei, ZHANG Kaixiang, et al. A method for interrupted-sampling repeater jamming identification and suppression based on differential features[J]. Journal of Radars, 2023, 12(1): 186–196. doi: 10.12000/JR22058 [11] 梁璞, 汪敏, 蒋彦雯, 等. 几何匹配滤波器及其对间歇采样转发干扰的响应特性[J/OL]. 现代雷达, 2022: 1–8. http://kns.cnki.net/kcms/detail/32.1353.TN.20220914.1638.004.html, 2022.LIANG Pu, WANG Min, JIANG Yanwen, et al. Geometric matched filter and it’s response to interrupted sampling repeater jamming[J/OL]. Modern Radar, 2022: 1–8. http://kns.cnki.net/kcms/detail/32.1353.TN.20220914.1638.004.html, 2022. [12] 刘一兵, 李金梁, 赵洋, 等. 基于小波系数相关性的间歇采样转发干扰识别[J]. 电子信息对抗技术, 2023, 38(1): 10–16. doi: 10.3969/j.issn.1674-2230.2023.01.002LIU Yibing, LI Jinliang, ZHAO Yang, et al. Interrupted-sampling and repeater jamming recognition based on wavelet coefficient correlation[J]. Electronic Information Warfare Technology, 2023, 38(1): 10–16. doi: 10.3969/j.issn.1674-2230.2023.01.002 [13] ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114 [14] ZHANG Yu, JIU Bo, WANG Penghui, et al. An end-to-end anti-jamming target detection method based on CNN[J]. IEEE Sensors Journal, 2021, 21(19): 21817–21828. doi: 10.1109/JSEN.2021.3103042 [15] LV Qinzhe, QUAN Yinghui, SHA Minghui, et al. Deep neural network-based interrupted sampling deceptive jamming countermeasure method[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 9073–9085. doi: 10.1109/JSTARS.2022.3214969 [16] 巩朋成, 吴云韬. 基于ADMM改进的低截获FDA-MIMO雷达发射波束设计[J]. 通信学报, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065GONG Pengcheng and WU Yuntao. Improved transmit beamforming design based on ADMM for low probability of intercept of FDA-MIMO radar[J]. Journal on Communications, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065 [17] 巩朋成, 王兆彬, 谭海明, 等. 杂波背景下基于交替方向乘子法的低截获频控阵MIMO雷达收发联合优化方法[J]. 电子与信息学报, 2021, 43(5): 1267–1274. doi: 10.11999/JEIT200445GONG Pengcheng, WANG Zhaobin, TAN Haiming, et al. Joint design of the transmit and receive beamforming via alternating direction method of multipliers for LPI of frequency diverse array MIMO radar in the presence of clutter[J]. Journal of Electronics &Information Technology, 2021, 43(5): 1267–1274. doi: 10.11999/JEIT200445 [18] 王福来, 庞晨, 黄大通, 等. 一种同时全极化雷达发射波形和接收滤波器联合设计的抗间歇采样转发干扰方法[J]. 中国科学:信息科学, 2022, 52(7): 1333–1348. doi: 10.1360/SSI-2021-0032 [19] XU Cheng, AUBRY A, CIUONZO D, et al. Robust waveform and filter bank design of polarimetric radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 370–384. doi: 10.1109/TAES.2017.2650619 [20] 陈强. 雷达极化中若干理论问题研究[D]. [博士论文], 国防科学技术大学, 2010.CHEN Qiang. Study on theoretical problems in radar polarimetry[D]. [Ph. D. dissertation], National University of Defense Technology, 2010. [21] 周万幸. 一种新型极化抗干扰技术研究[J]. 电子学报, 2009, 37(3): 454–458. doi: 10.3321/j.issn:0372-2112.2009.03.005ZHOU Wanxing. Research of a new type techniques for anti-interference using polarization[J]. Acta Electronica Sinica, 2009, 37(3): 454–458. doi: 10.3321/j.issn:0372-2112.2009.03.005 [22] 刘勇, 李永桢, 王雪松, 等. 基于极化分集接收的HRRP欺骗干扰鉴别[J]. 系统工程与电子技术, 2011, 33(6): 1247–1252.LIU Yong, LI Yongzhen, WANG Xuesong, et al. Discrimination of HRRP deception jamming based on polarization diversity receiving[J]. Systems Engineering and Electronics, 33(6): 1247–1252. [23] SONG Junxiao, BABU P, and PALOMAR D P. Sequence design to minimize the weighted integrated and peak sidelobe levels[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2051–2064. doi: 10.1109/TSP.2015.2510982 [24] SONG Junxiao, BABU P, and PALOMAR D P. Optimization methods for designing sequences with low autocorrelation sidelobes[J]. IEEE Transactions on Signal Processing, 2015, 63(15): 3998–4009. doi: 10.1109/TSP.2015.2425808 [25] ZHAO Licheng, SONG Junxiao, BABU P, et al. A unified framework for low autocorrelation sequence design via majorization–minimization[J]. IEEE Transactions on Signal Processing, 2017, 65(2): 438–453. doi: 10.1109/TSP.2016.2620113 [26] GTRI public dataset[OL]. https://www.sdms.afrl.af.mil/index.php?collection=gtri, 2022. -





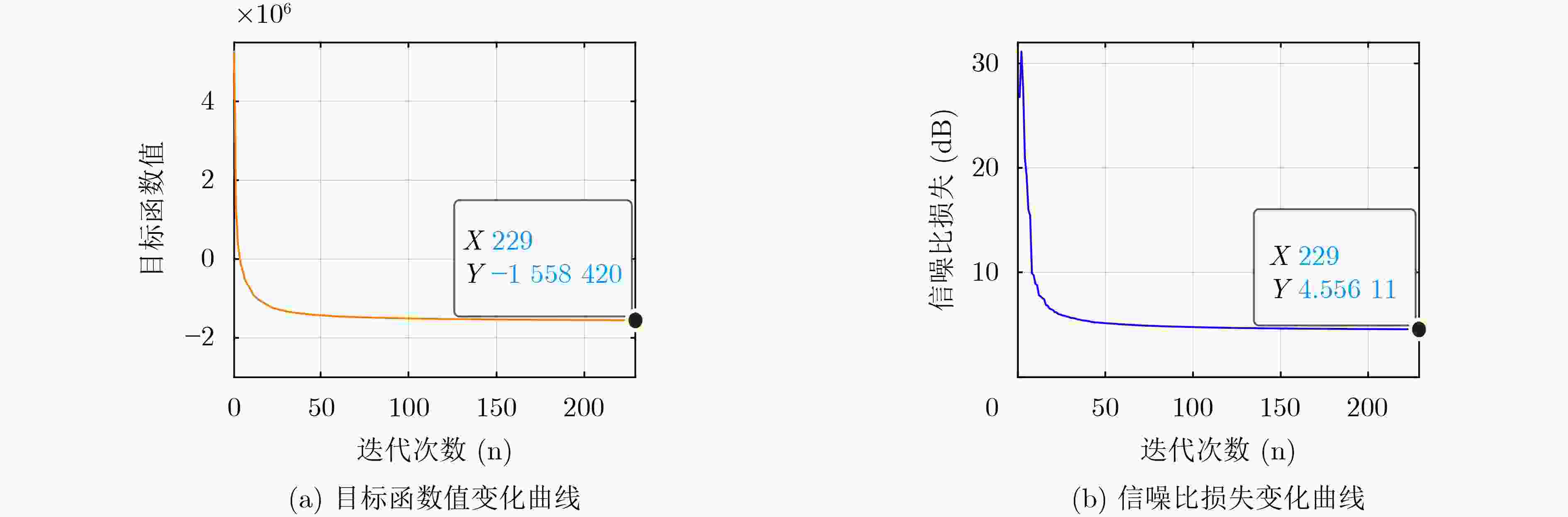
 下载:
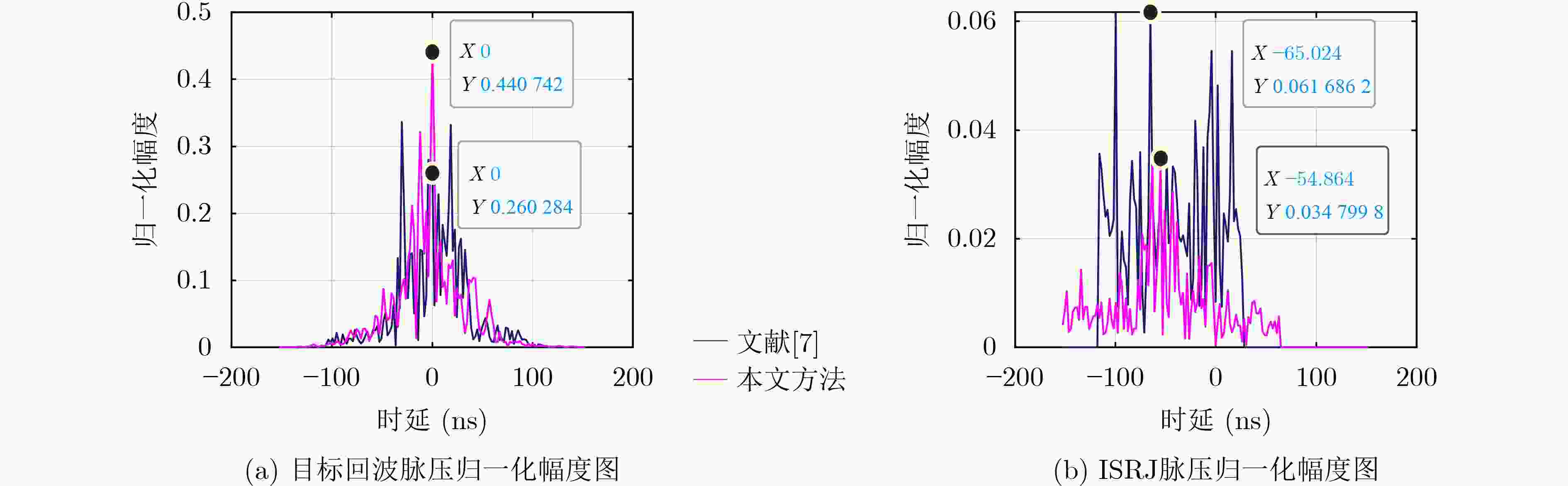
下载:
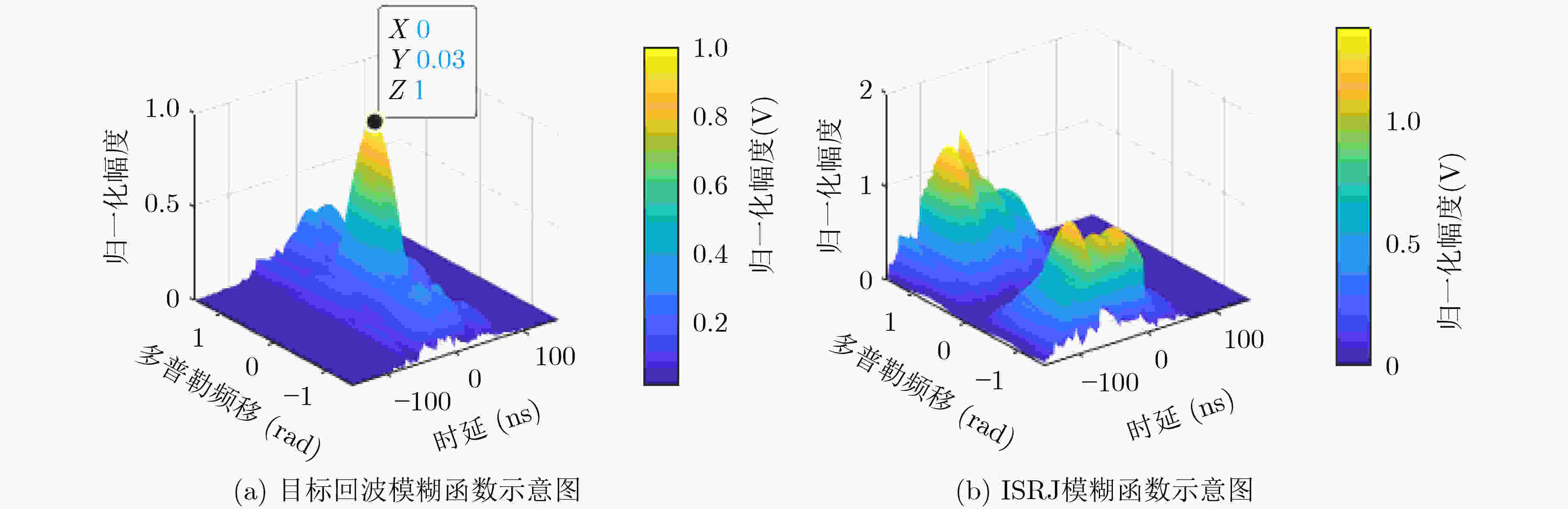


 下载:
下载:
