Adversarial Defense Algorithm Based on Momentum Enhanced Future Map
-
摘要: 深度神经网络(DNN)因其优异的性能而被广泛应用，但易受对抗样本攻击的问题使其面临巨大的安全风险。通过对DNN的卷积过程进行可视化，发现随着卷积层数加深，对抗攻击对原始输入产生的扰动愈加明显。基于这一发现，采用动量法中前向结果修正后向结果的思想，该文提出一种基于动量增强特征图的防御算法(MEF)。MEF算法在DNN的卷积层上部署特征增强层构成特征增强块(FEB)，FEB会结合原始输入以及浅层卷积层的特征图生成特征增强图，进而利用特征增强图来增强深层的特征图。同时，为了保证每层特征增强图的有效性，增强后的特征图还会对特征增强图进行进一步更新。为验证MEF算法的有效性，使用多种白盒与黑盒攻击对部署MEF算法的DNN模型进行攻击实验，结果表明在投影梯度下降法(PGD)以及快速梯度符号法(FGSM)的攻击实验中，MEF算法对对抗样本的识别精度比对抗训练(AT)高出3%～5%，且对干净样本的识别精度也有所提升。此外，使用比训练时更强的对抗攻击方法进行测试时，与目前先进的噪声注入算法(PNI)以及特征扰动算法(L2P)相比，MEF算法表现出更强的鲁棒性。Abstract: Deep Neural Networks (DNN) are widely used due to their excellent performance, but the problem of being vulnerable to adversarial examples makes them face huge security risks.Through the visualization of the convolution process of DNN, it is found that with the deepening of the convolution layers, the disturbance of the original input caused by the adversarial attack becomes more obvious. Based on this finding, a defense algorithm based on Momentum Enhanced Feature maps (MEF) is proposed by adopting the idea of revising the backward results by the forward results in the momentum method. The MEF algorithm deploys a feature enhancement layer on the convolutional layer of the DNN to form a Feature Enhancement Block (FEB). The FEB combines the original input and the feature map of the shallow convolutional layer to generate a feature enhancement map, and then uses the feature enhancement map to enhance the deep features map. While, in order to ensure the effectiveness of the feature enhancement map of each layer, the enhanced feature map will further update the feature enhancement map. In order to verify the effectiveness of the MEF algorithm, various white-box and black-box attacks are used to attack the DNN model deployed with the MEF algorithm, the results show that in the Project Gradient Descent (PGD) and Fast Gradient Sign Method (FGSM) attack experiment, the recognition accuracy of MEF algorithm for adversarial samples is 3%～5% higher than that of Adversarial Training (AT), and the recognition accuracy of clean samples is also improved. Furthermore, when tested with stronger adversarial attack methods than training, the MEF algorithm exhibits stronger robustness compared with the currently advanced Parametric Noise Injection algorithm (PNI) and Learn2Perturb algorithm (L2P).
-
算法1 MEF算法 输入：训练集$ D = \{ ({X_i},{t_i}),i = 1,2,\cdots,n\} $，训练周期$ I $，
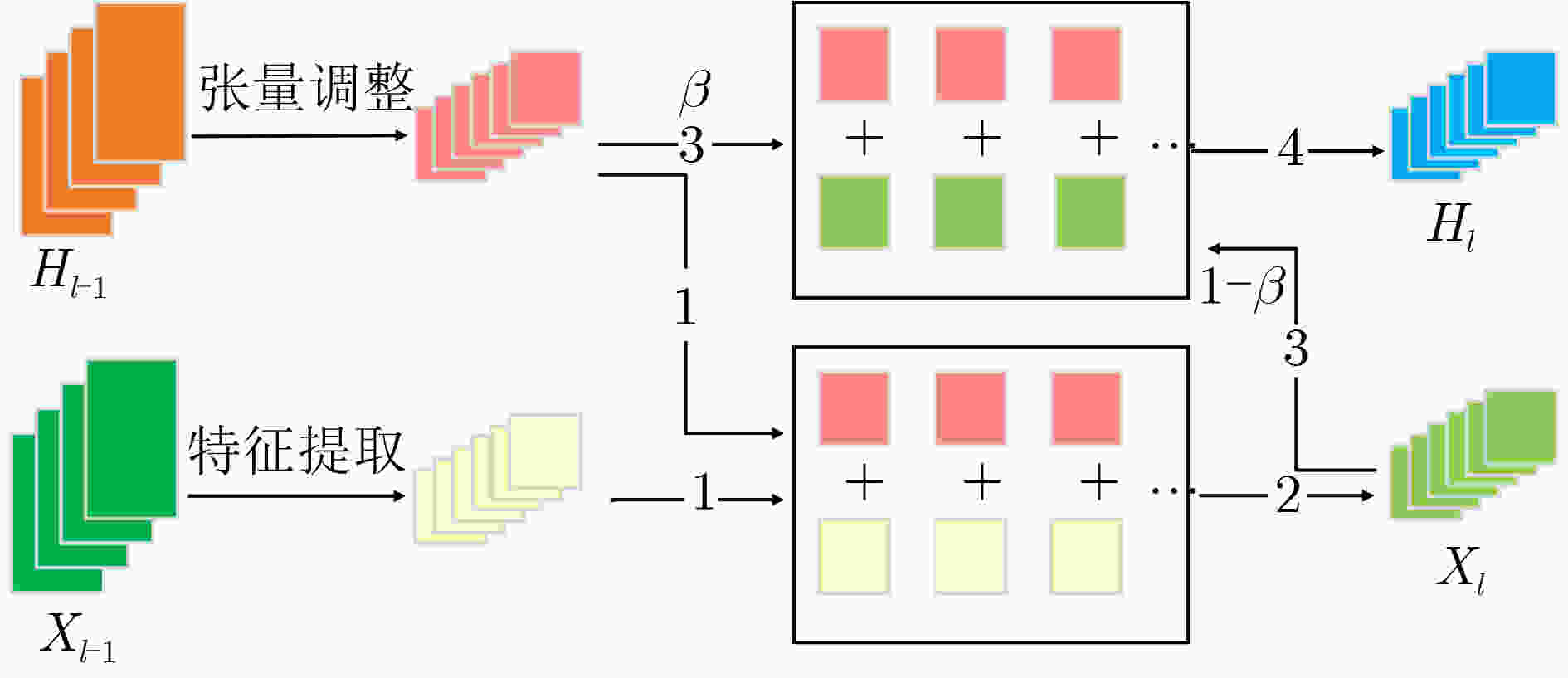
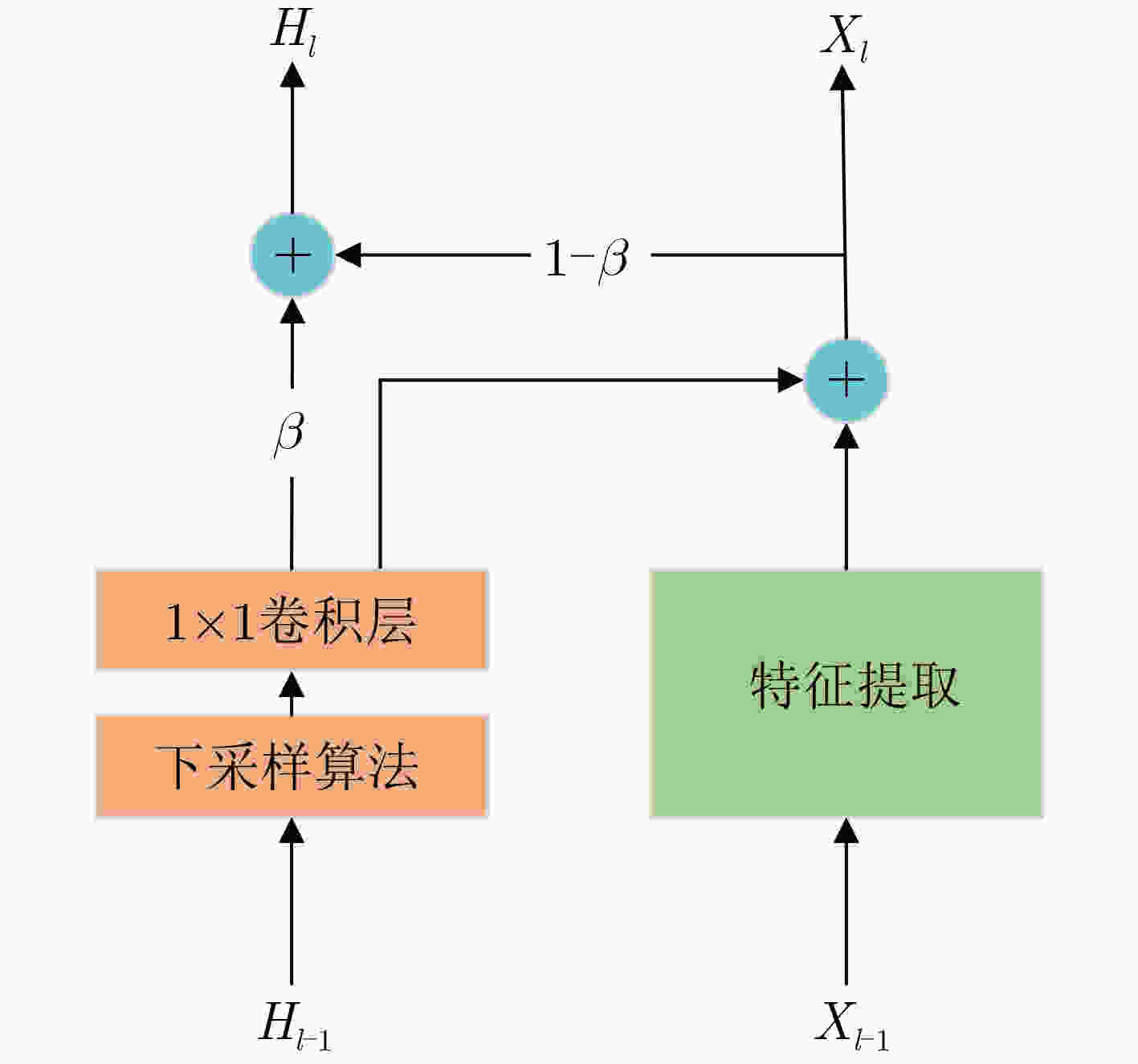
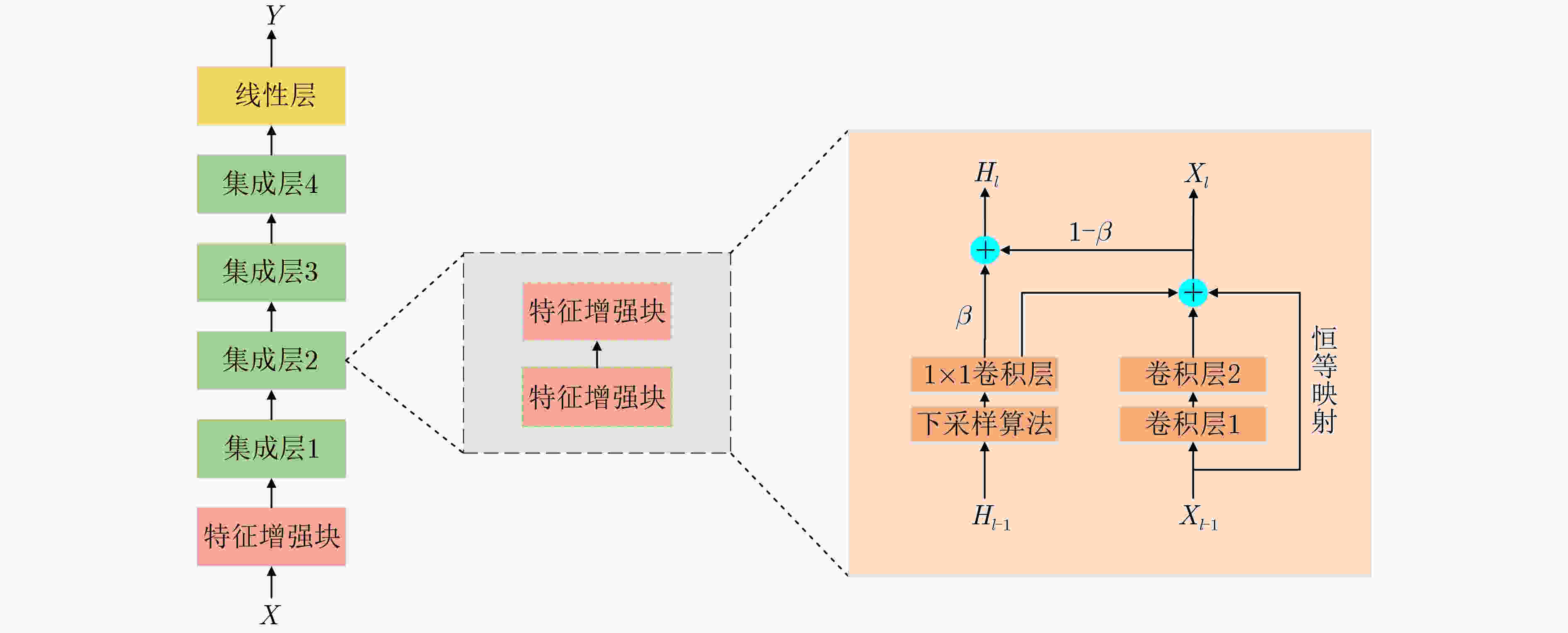
动量参数$ \beta $，初始化模型参数$ W $，交叉熵损失函数$ L( \cdot ) $输出：训练模型DNN (1) $ {H_i} = {X_i} $ /*$ {H_i} $是$ {X_i} $的初始特征增强图*/ (2) for epoch $ I $ (3) for $ k $ /*$ k $是卷积层*/ (4) $f'_k = {\text{conv} }(f_{k - 1}^{})$ /*conv指卷积操作，$f'_k$指本层未增
强的特征图，$ {f_{k - 1}} $指上层特征图*/(5) $h'_k = {\text{crop} }({h_{k - 1} })$ /*crop指对上层增强图的裁剪操作*/ (6) ${f_k} = f'_k + h'_k$ /*$ {f_k} $是本层最终特征图*/ (7) ${h_k} = \beta \cdot h'_k + (1 - \beta ) \cdot {f_k}$ /*$ {h_k} $是本层最终特征增强图* (8) end for (9) update $ W $ based on the loss function $ L( \cdot ) $ (10) end for 
下载: 导出CSV
表 3 C&W攻击中MEF算法与AT算法对抗样本的$ {L_2} $距离对比
防御算法 置信度$ K $ 0 0.1 1.0 2.0 5.0 MEF 8.657 8.831 10.012 11.279 17.229 AT 5.468 5.606 6.794 8.095 12.029
下载: 导出CSV
表 5 PNI, L2P, HFA以及MEF算法的对比试验
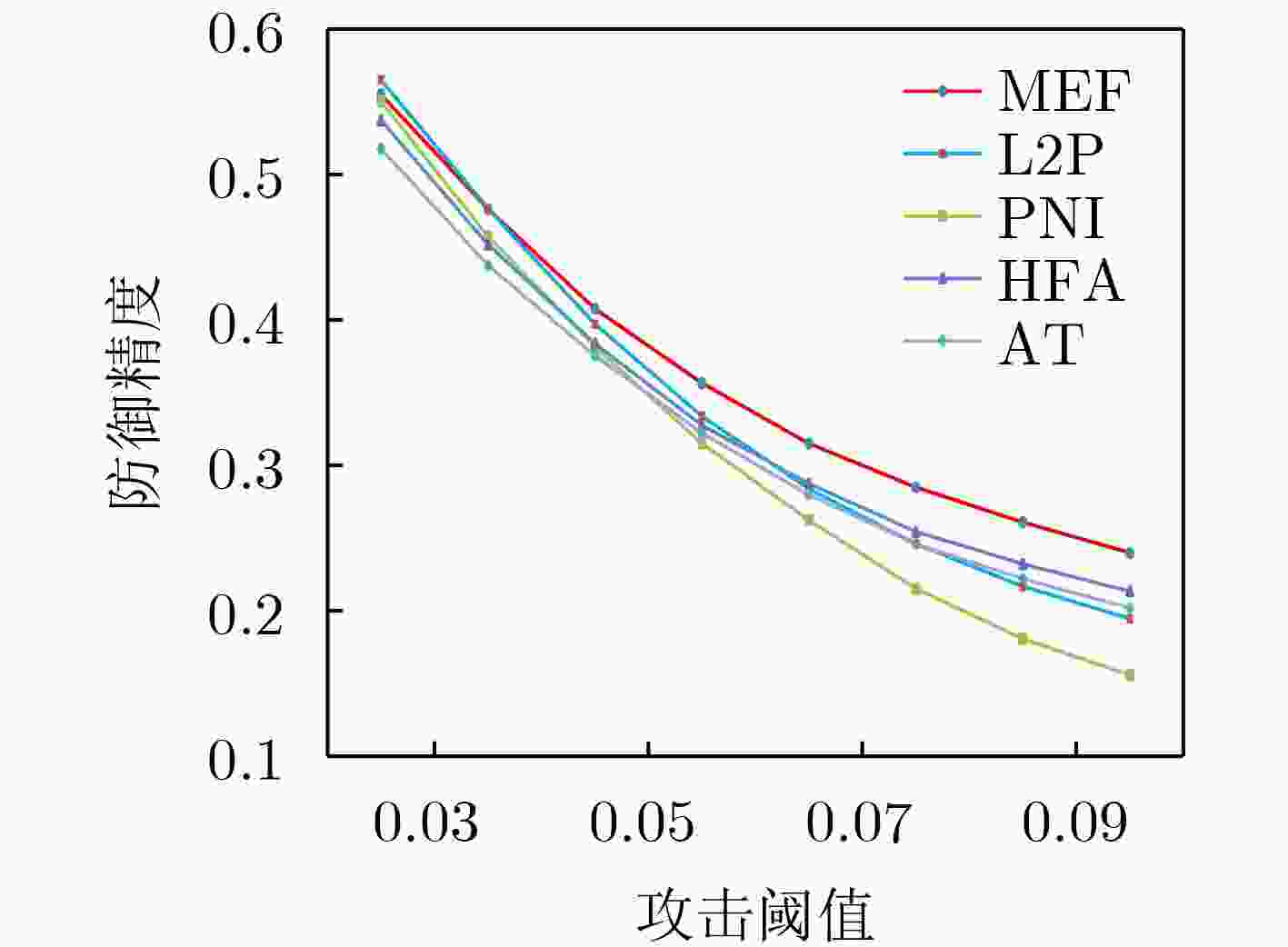
攻击阈值$ \varepsilon $ 迭代次数$ N $ PNI L2P HFA MEF 0.03 10 47.21 47.39 44.27 46.33 20 45.41 44.76 42.05 45.07 30 44.94 44.34 41.65 44.80 防御精度均值 45.85 45.50 42.66 45.40 0.06 10 20.72 21.44 17.43 20.39 20 12.69 12.92 11.24 13.42 30 11.58 10.99 9.87 11.73 防御精度均值 15.00 15.12 12.85 15.18 0.07 10 17.10 18.09 15.02 16.87 20 8.09 8.30 7.17 9.19 30 6.41 6.28 5.26 7.62 防御精度均值 10.53 10.89 9.15 11.23 干净样本识别精度 82.04 84.29 82.31 84.44
下载: 导出CSV
表 6 MEF的非模糊梯度测试
模糊梯度的特征 通过 (1) 单步攻击性能优于迭代攻击 √ (2) 黑盒攻击优于白盒攻击 √ (3) 无界扰动攻击无法达到100%成功率 √ (4) 基于梯度的攻击无法生成对抗样本 √ (5) 提高扰动阈值不会增加成功率 √
下载: 导出CSV
-
[1] MAULUD D H, ZEEBAREE S R M, JACKSI K, et al. State of art for semantic analysis of natural language processing[J]. Qubahan Academic Journal, 2021, 1(2): 21–28. doi: 10.48161/qaj.v1n2a44 [2] ALHARBI S, ALRAZGAN M, ALRASHED A, et al. Automatic speech recognition: Systematic literature review[J]. IEEE Access, 2021, 9: 131858–131876. doi: 10.1109/ACCESS.2021.3112535 [3] 陈怡, 唐迪, 邹维. 基于深度学习的Android恶意软件检测: 成果与挑战[J]. 电子与信息学报, 2020, 42(9): 2082–2094. doi: 10.11999/JEIT200009CHEN Yi, TANG Di, and ZOU Wei. Android malware detection based on deep learning: Achievements and challenges[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2082–2094. doi: 10.11999/JEIT200009 [4] SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]. 2nd International Conference on Learning Representations, Banff, Canada, 2014. [5] GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015. [6] MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [7] CARLINI N and WAGNER D. Towards evaluating the robustness of neural networks[C]. 2017 IEEE Symposium on Security and Privacy (SP), San Jose, USA, 2017: 39–57. [8] LIU Yanpei, CHEN Xinyun, LIU Chang, et al. Delving into transferable adversarial examples and black-box attacks[C]. 5th International Conference on Learning Representations, Toulon, France, 2017. [9] ANDRIUSHCHENKO M, CROCE F, FLAMMARION N, et al. Square attack: A query-efficient black-box adversarial attack via random search[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 484–501. [10] LIN Jiadong, SONG Chuanbiao, HE Kun, et al. Nesterov accelerated gradient and scale invariance for adversarial attacks[C]. 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [11] 邹军华, 段晔鑫, 任传伦, 等. 基于噪声初始化、Adam-Nesterov方法和准双曲动量方法的对抗样本生成方法[J]. 电子学报, 2022, 50(1): 207–216. doi: 10.12263/DZXB.20200839ZOU Junhua, DUAN Yexin, REN Chuanlun, et al. Perturbation initialization, Adam-Nesterov and Quasi-Hyperbolic momentum for adversarial examples[J]. Acta Electronica Sinica, 2022, 50(1): 207–216. doi: 10.12263/DZXB.20200839 [12] XU Weilin, EVANS D, and QI Yanjun. Feature squeezing: Detecting adversarial examples in deep neural networks[C]. 2018 Network and Distributed System Security Symposium (NDSS), San Diego, USA, 2018. [13] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929–1958. [14] DHILLON G S, AZIZZADENESHELI K, LIPTON Z C, et al. Stochastic activation pruning for robust adversarial defense[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [15] VIEVK B S and BABU R V. Single-step adversarial training with dropout scheduling[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 947–956. [16] MENG Dongyu and CHEN Hao. MagNet: A two-pronged defense against adversarial examples[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 135–147. [17] SONG Yang, KIM T, NOWOZIN S, et al. PixelDefend: Leveraging generative models to understand and defend against adversarial examples[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [18] PAPERNOT N, MCDANIEL P, WU Xi, et al. Distillation as a defense to adversarial perturbations against deep neural networks[C]. 2016 IEEE Symposium on Security and Privacy (SP), San Jose, USA, 2016: 582–597. [19] XIE Cihang, WU Yuxin, VAN DER MAATEN L, et al. Feature denoising for improving adversarial robustness[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 501–509. [20] HE Zhezhi, RAKIN A S, and FAN Deliang. Parametric noise injection: Trainable randomness to improve deep neural network robustness against adversarial attack[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 588–597. [21] JEDDI A, SHAFIEE M J, KARG M, et al. Learn2Perturb: An end-to-end feature perturbation learning to improve adversarial robustness[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 1238–1247. [22] ZHANG Xiaoqin, WANG Jinxin, WANG Tao, et al. Robust feature learning for adversarial defense via hierarchical feature alignment[J]. Information Sciences, 2021, 560: 256–270. doi: 10.1016/J.INS.2020.12.042 [23] XIAO Chang and ZHENG Changxi. One man's trash is another man's treasure: Resisting adversarial examples by adversarial examples[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 409–418. [24] ATHALYE A, CARLINI N, and WAGNER D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples[C]. The 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 274–283. -
图(7) / 表(7)
计量
- 文章访问数: 284
- HTML全文浏览量: 216
- PDF下载量: 95
- 被引次数: 0
下载:
