Research on Combination Waveform Design Based on Hyperbolic Frequency Modulation
-
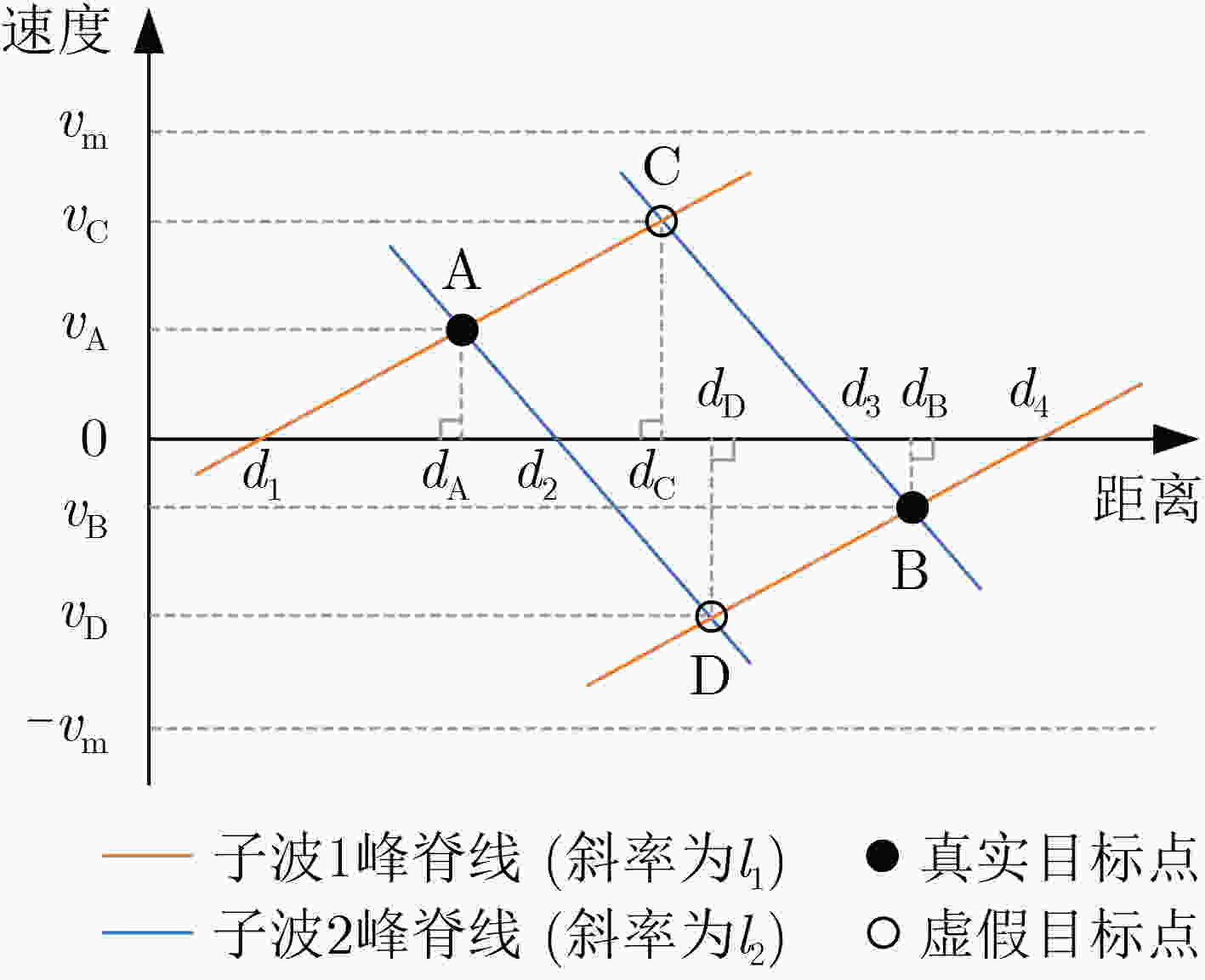
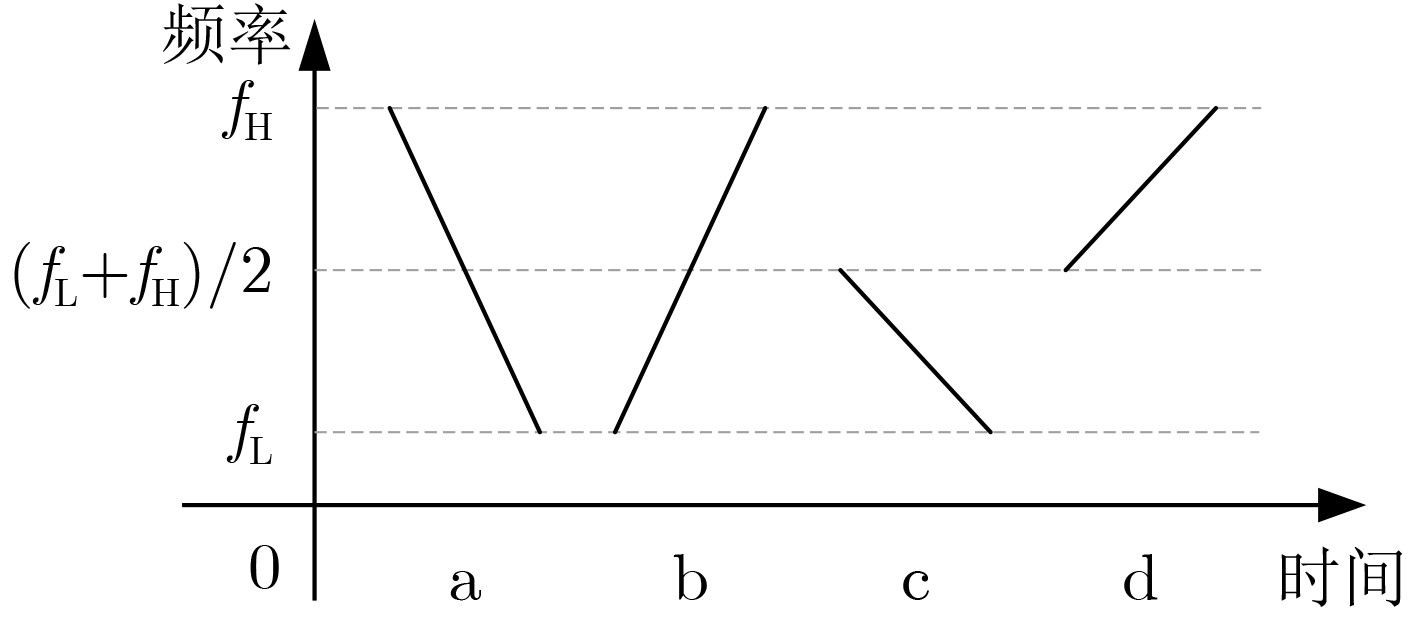
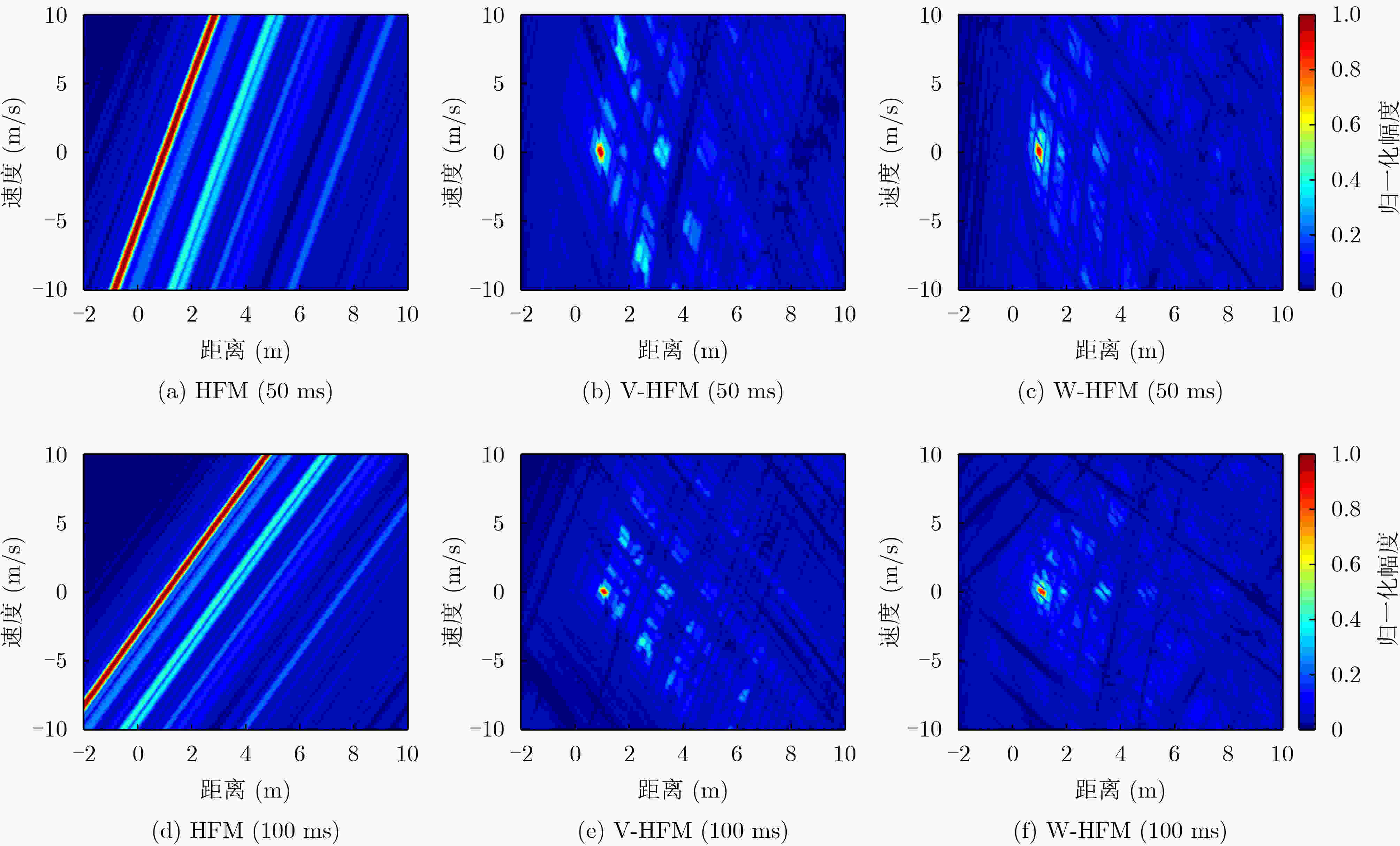
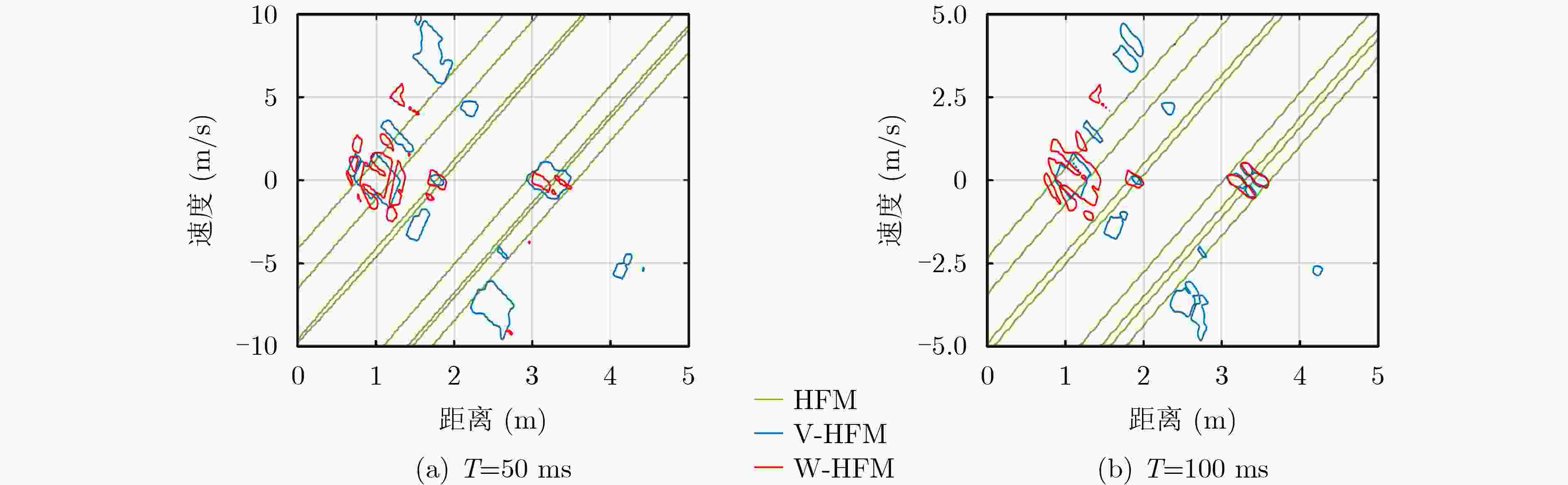
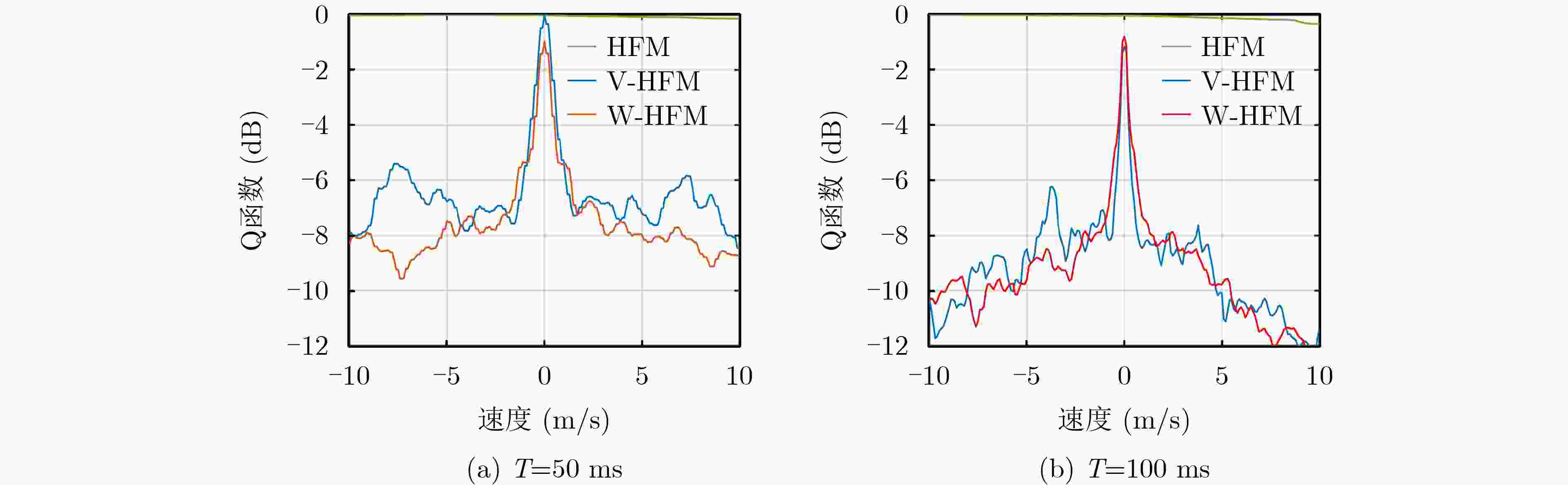
摘要: 主动声呐通常采用的单频或调频波形时频耦合分辨能力弱,不利于混响背景下的信号检测与估计。先前工作表明,“V”和“W”形双曲调频(HFM)组合波形可以实现距离-速度高分辨和低混响输出,其中W-HFM波形还有效解决了V-HFM波形在多目标场景中的虚假目标问题,但是设计复杂、运算量大。为优化HFM组合波形的设计和应用,该文推导了HFM组合波形的峰脊线斜率表达式。一方面提出V-HFM波形的最小无虚警距离(MNFAD)指标,分析了其多目标适用性;另一方面以典型的W-HFM波形为例,提出了优化的波形设计方案,对工程应用具有指导意义。水池实验数据表明,HFM组合波形实现了距离-速度高分辨、混响输出降低5 dB以上,并且W-HFM波形还抑制了虚假目标干扰。Abstract: The single frequency or modulated frequency waveform employed in active Sound Navigation and Ranging (SONAR) systems yields inferior range or velocity resolution. This deficiency impairs signal detection and estimation in reverberation background. Previous work demonstrates that “V” and “W” type Hyperbolic Frequency Modulation (HFM) combination waveforms substantially enhance range–velocity resolution while simultaneously reducing reverberation. The W-HFM waveform serves as an effective solution to the false-target problem inherent in the V-HFM waveform when applied to multiple-target scenarios. However, the complex design and extensive computation required pose considerable challenges. Thus, the ridge slope equation of HFM combination waveforms is derived to optimize their design and application. Furthermore, the minimum no false alarm distance index of the V-HFM waveform is proposed, and its applicability in multiple-target scenarios is analyzed. Additionally, an optimized waveform design scheme is proposed, using the typical W-HFM waveform as an example, which can serve as a guide for engineering applications. Tank experimental data reveal that the HFM combination waveform achieves high range–velocity resolution, reverberation is reduced by more than 5 dB, and the W-HFM waveform suppresses false target interference.
-
表 1 组合结果
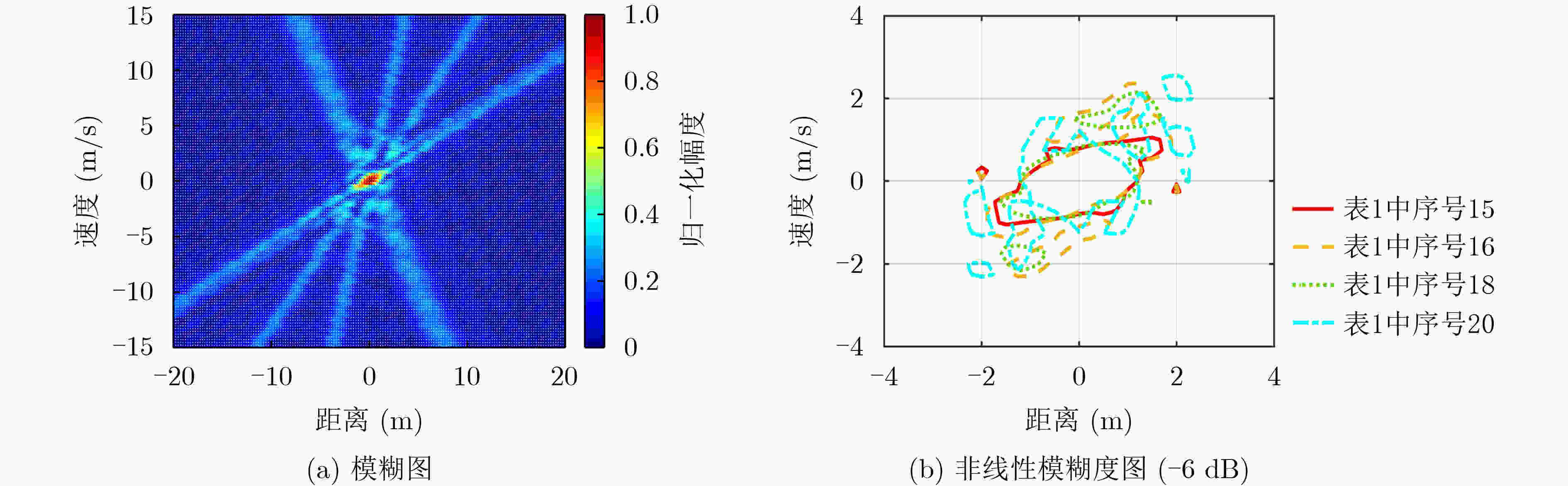
序号 组合顺序 最小夹角(°) 跳频点数 序号 组合顺序 最小夹角(°) 跳频点数 1 a-b-c-d 0 2 13 c-a-b-d 16.4 2 2 a-b-d-c 6.9 2 14 c-a-d-b 8.1 3 3 a-c-b-d 6.5 2 15 c-b-a-d 21.8 1 4 a-c-d-b 6.5 3 16 c-b-d-a 18.4 1 5 a-d-b-c 6.9 3 17 c-d-a-b 4.3 1 6 a-d-c-b 0 2 18 c-d-b-a 9.2 2 7 b-a-c-d 6.9 2 19 d-a-b-c 0 1 8 b-a-d-c 0 2 20 d-a-c-b 0 1 9 b-c-a-d 20.6 3 21 d-b-a-c 7.1 2 10 b-c-d-a 13.4 2 22 d-b-c-a 10.3 3 11 b-d-a-c 7.1 2 23 d-c-a-b 0 2 12 b-d-c-a 13.4 3 24 d-c-b-a 4.9 1 表 2 回波理论距离
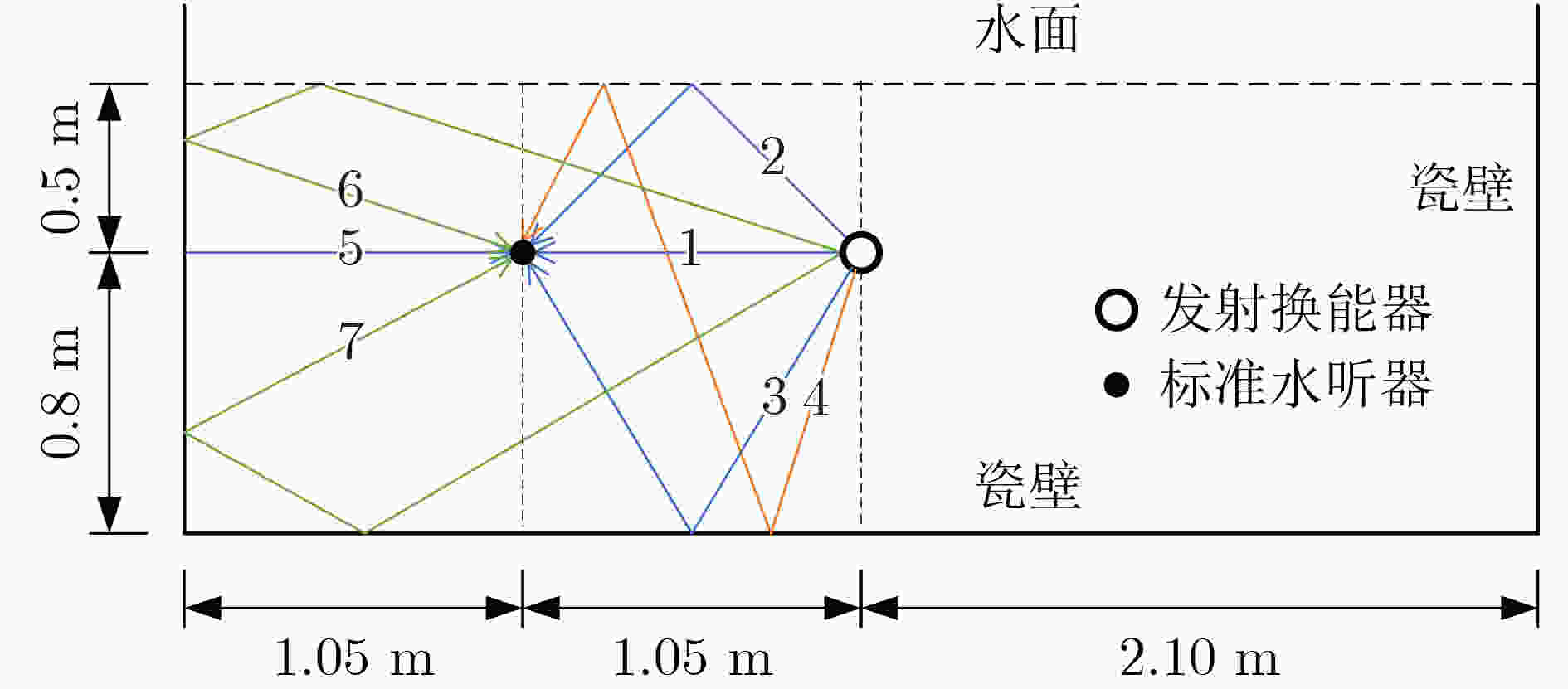
序号 理论距离(m) 1 1.05 2 1.45 3 1.91 4 2.80 5 3.15 6 3.30 7 3.53 -
[1] 游波, 张卫, 郭瑞. 声纳主动探测中的最佳波形选择问题[J]. 火力与指挥控制, 2013, 38(3): 151–153,157. doi: 10.3969/j.issn.1002-0640.2013.03.039YOU Bo, ZHANG Wei, and GUO Rui. Waveform selection proposition in active sonar detection[J]. Fire Control &Command Control, 2013, 38(3): 151–153,157. doi: 10.3969/j.issn.1002-0640.2013.03.039 [2] WAITE A D. Sonar for Practising Engineers[M]. 3rd ed. Chichester: John Wiley & Sons, 2002: 192–197. [3] MURRAY J J. On the Doppler bias of hyperbolic frequency modulation matched filter time of arrival estimates[J]. IEEE Journal of Oceanic Engineering, 2019, 44(2): 446–450. doi: 10.1109/JOE.2018.2819779 [4] HAGUE D A. Adaptive transmit waveform design: An enabler for cognitive active sonar[J]. Sea Technology, 2021, 62(11): 12–14. [5] WANG Yan, HE Yuliang, WANG Jinjin, et al. Comb waveform optimisation with low peak-to-average power ratio via alternating projection[J]. IET Radar, Sonar & Navigation, 2018, 12(9): 1012–1020. doi: 10.1049/iet-rsn.2018.0039 [6] HAGUE D A and BUCK J R. An experimental evaluation of the generalized sinusoidal frequency modulated waveform for active sonar systems[J]. Journal of the Acoustical Society of America, 2019, 145(6): 3741–3755. doi: 10.1121/1.5113581 [7] 周胜增, 杜选民. 利用正弦调频信号的宽带速度敏感特性抑制混响[J]. 声学学报, 2022, 47(1): 16–26. doi: 10.15949/j.cnki.0371-0025.2022.01.002ZHOU Shengzeng and DU Xuanmin. Reverberation suppression by utilizing wideband speed sensitive characteristic of sinusoidal frequency modulation signal[J]. Acta Acustica, 2022, 47(1): 16–26. doi: 10.15949/j.cnki.0371-0025.2022.01.002 [8] 曾凌川, 白燕, 卢晓春, 等. 一种基于调制m序列的直接序列扩频信号调制方法[J]. 电子与信息学报, 2021, 43(8): 2156–2164. doi: 10.11999/JEIT200600ZENG Lingchuan, BAI Yan, LU Xiaochun, et al. A signal modulation method of direct sequence spread spectrum based on modulated m-sequence[J]. Journal of Electronics &Information Technology, 2021, 43(8): 2156–2164. doi: 10.11999/JEIT200600 [9] GUAN Chengyu, ZHOU Zemin, and ZENG Xinwu. A phase-coded sequence design method for active sonar[J]. Sensors, 2020, 20(17): 4659. doi: 10.3390/s20174659 [10] 宁晓燕, 梁洪广, 王震铎, 等. 二维随机跳频系统性能分析[J]. 哈尔滨工程大学学报, 2022, 43(2): 274–281. doi: 10.11990/jheu.202012012NING Xiaoyan, LIANG Hongguang, WANG Zhenduo, et al. Performance analysis of a two-dimensional random frequency hopping system[J]. Journal of Harbin Engineering University, 2022, 43(2): 274–281. doi: 10.11990/jheu.202012012 [11] PAN Pingping, LIU Hui, ZHANG Yixiong, et al. Range, radial velocity, and acceleration MLE using frequency modulation coded LFM pulse train[J]. Digital Signal Processing, 2017, 60: 252–261. doi: 10.1016/j.dsp.2016.09.009 [12] KUNDU N K, MALLIK R K, and MCKAY M R. Signal design for frequency-phase keying[J]. IEEE Transactions on Wireless Communications, 2020, 19(6): 4067–4079. doi: 10.1109/TWC.2020.2979718 [13] NEUBERGER N and VEHMAS R. A Costas-based waveform for local range-Doppler sidelobe level reduction[J]. IEEE Signal Processing Letters, 2021, 28: 673–677. doi: 10.1109/LSP.2021.3067219 [14] VESPE M, JONES G, and BAKER C J. Lessons for radar: Waveform diversity in echolocating mammals[J]. IEEE Signal Processing Magazine, 2009, 26(1): 65–75. doi: 10.1109/MSP.2008.930412 [15] RASOOL S B and BELL M R. Biologically inspired processing of radar waveforms for enhanced delay-Doppler resolution[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2698–2709. doi: 10.1109/TSP.2011.2121904 [16] ZHU Jiahua, SONG Yongping, FAN Chongyi, et al. Nonlinear processing for enhanced delay-Doppler resolution of multiple targets based on an improved radar waveform[J]. Signal Processing, 2017, 130: 355–364. doi: 10.1016/j.sigpro.2016.07.025 [17] 郭瑞, 蔡志明, 姚直象. 主动声纳组合波形设计技术的发展现状和趋势[C]. 中国声学学会水声学分会2015年学术会议论文集, 武汉, 2015: 235–238.GUO Rui, CAI Zhiming, and YAO Zhixiang. The status and current of the hybrid waveforms design technology for active sonar[C]. Proceedings of the 2015 Academic Conference of the Underwater Acoustics Branch of the Chinese Acoustic Society, Wuhan, China: 2015: 235–238. [18] 娄良轲, 王平波. 一种基于双曲调频组合的高分辨波形设计[J]. 舰船电子工程, 2020, 40(10): 154–158. doi: 10.3969/j.issn.1672-9730.2020.10.037LOU Liangke and WANG Pingbo. A high resolution waveform design based on hyperbolic frequency modulation combination[J]. Ship Electronic Engineering, 2020, 40(10): 154–158. doi: 10.3969/j.issn.1672-9730.2020.10.037 -





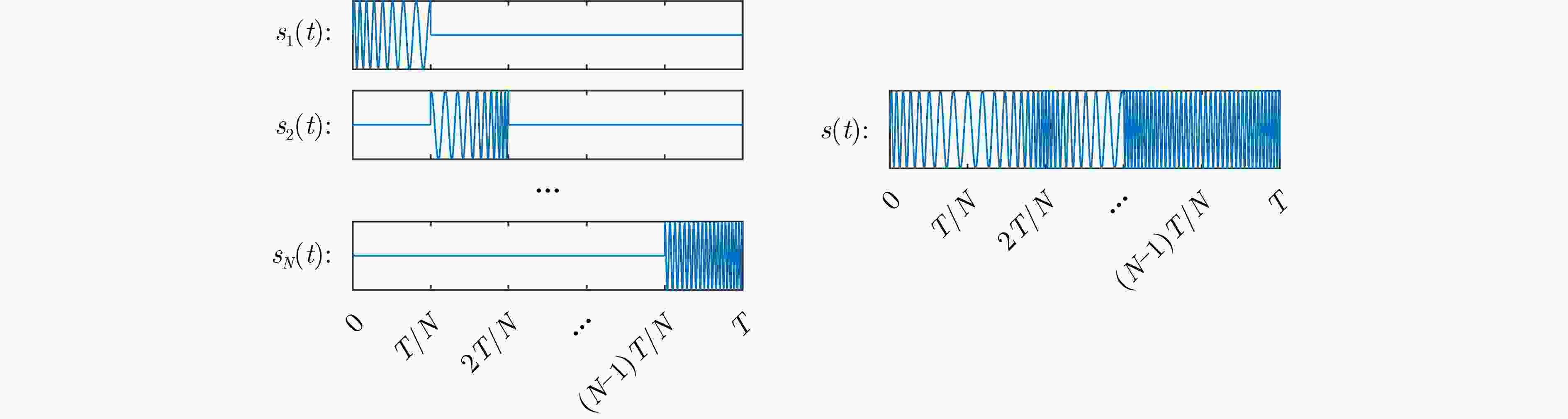
 下载:
下载:
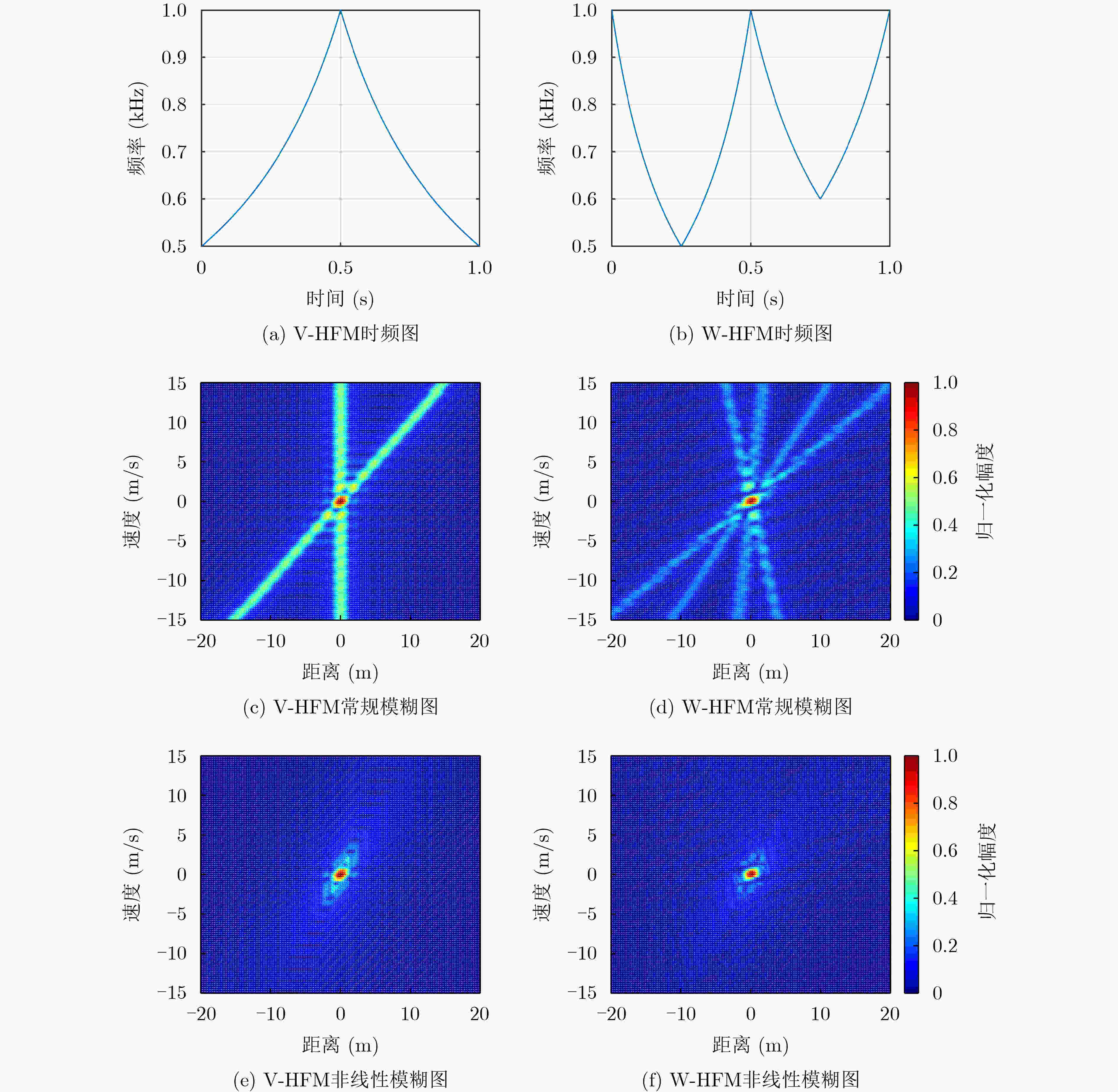
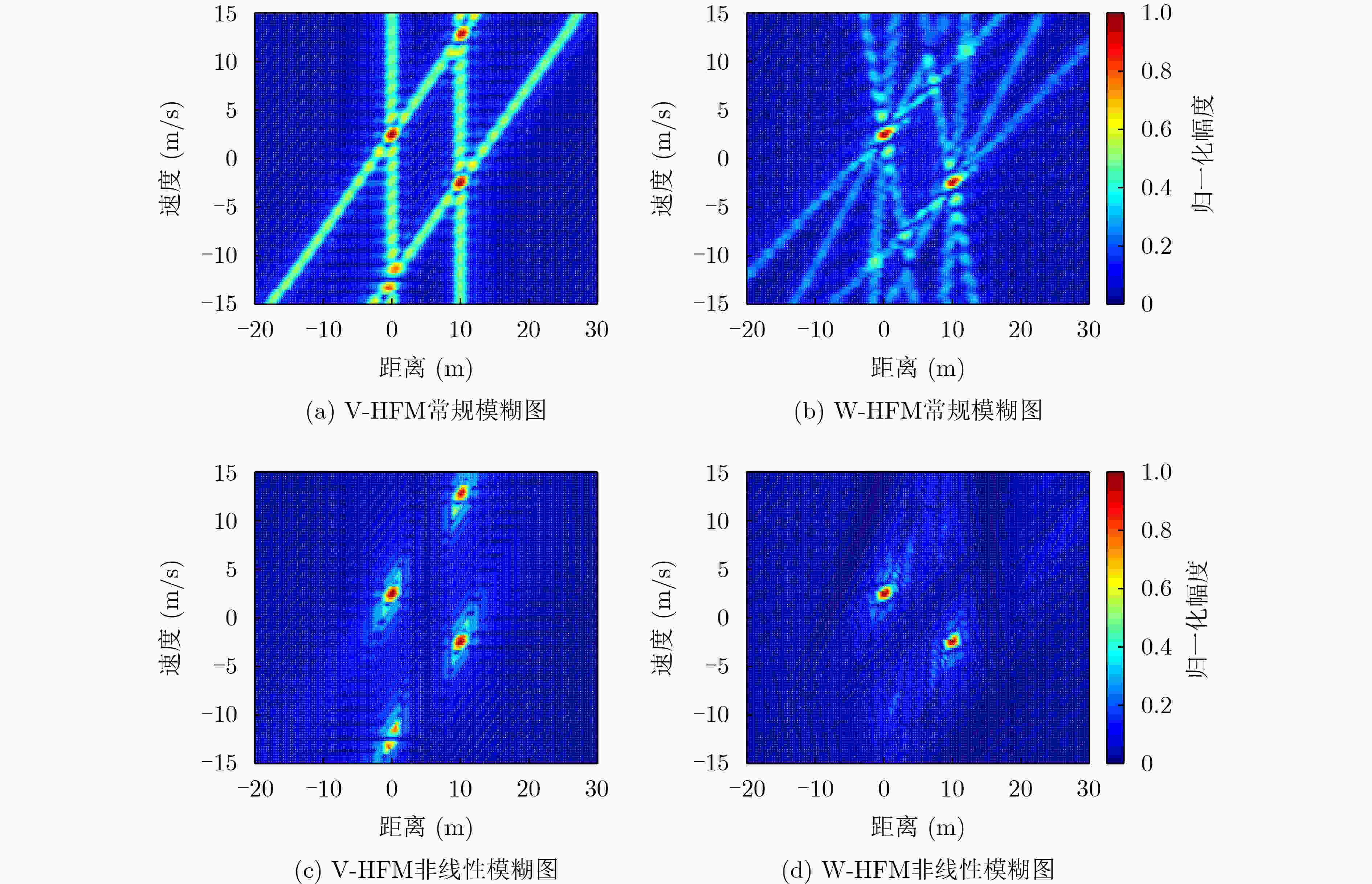
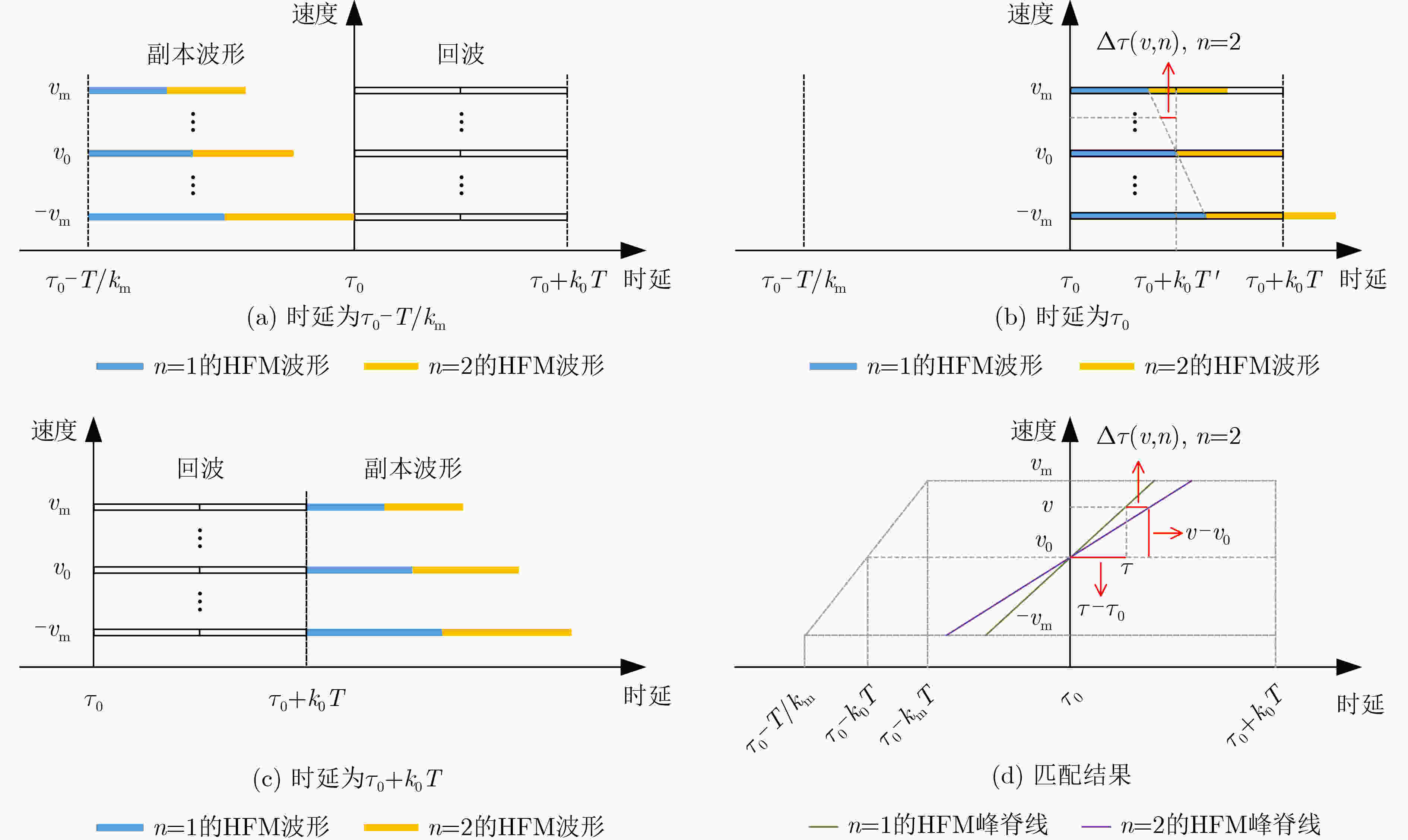


 下载:
下载:
