利用多路选择器熵源的高移植性轻量级物理不可克隆函数研究

姚亮; 梁华国; 杨世豪; 章宏; 鲁迎春

doi:10.11999/JEIT221263

利用多路选择器熵源的高移植性轻量级物理不可克隆函数研究

doi: 10.11999/JEIT221263

合肥工业大学微电子学院合肥 230009

基金项目: 国家自然科学基金(62174048)

详细信息

作者简介:
姚亮：男，博士生，研究方向为硬件安全及集成电路设计

梁华国：男，教授，博士生导师，研究方向为集成电路测试、数字系统设计自动化及硬件安全

杨世豪：男，硕士生，研究方向为硬件安全及高速数据传输

章宏：女，博士生，研究方向为集成电路测试及电路模型构建

鲁迎春：男，副教授，硕士生导师，研究方向为硬件安全

通讯作者:
鲁迎春　luyingchun@hfut.edu.cn

中图分类号: TN402
计量
- 文章访问数: 584
- HTML全文浏览量: 497
- PDF下载量: 74
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-30
- 修回日期: 2022-12-21
- 网络出版日期: 2022-12-23
- 刊出日期: 2023-01-17

Research on Highly Portable Lightweight Physical Unclonable Functions Using Multiplexer Entropy Sources

School of Microelectronics, Hefei University of Technology, Hefei 230009, China

Funds: The National Natural Science Foundation of China (62174048)

摘要

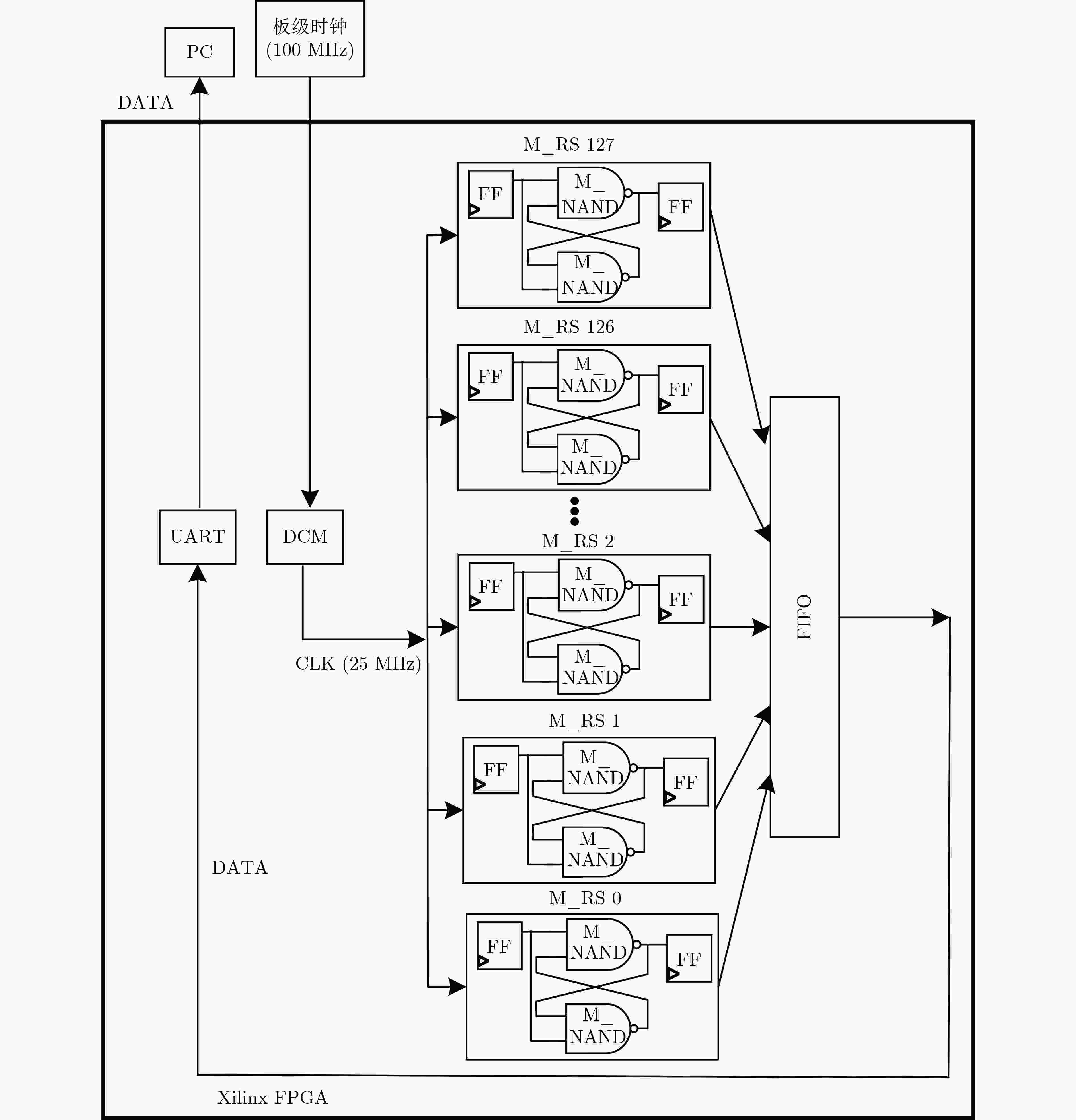
摘要: SR锁存器物理不可克隆函数 (Physical Unclonable Function, PUF) 是基于 FPGA 实现的最流行加密应用，在轻量级物联网设备中拥有广阔的市场。为了实现对称无偏SR锁存PUF，研究人员提出了不同的实现方法，这些方法增加了面积消耗。该文提出一种新型的基于MUX单元的延迟门来构成M_SR PUF单元，并将稳定状态下SR锁存器的输出提取作为PUF的响应。为了验证所提出的 M_SR PUF，该文在 Xilinx Virtex-6,Virtex-7 和 Kintex-7 3个系列的 FPGA 上进行了实现。值得一提的是，对称布局通过“硬宏”实现相对简单，保证了PUF更好的性能。实验结果表明，所提出的M_SR PUF可以在超宽范围的环境变化(温度：0°C～80°C；电压：0.8～1.2 V)下稳定工作，平均唯一性为50.125%。此外，所提出的 M_SR PUF 单元具有低开销的特点，仅消耗 4个 MUX 和 2个 DFF，并产生适合硬件安全应用的高熵响应。
- 硬件安全 /
- 物理不可克隆功能 /
- 对称布局 /
- 可移植性 /
- 低面积开销
Abstract: SR Latches Physical Unclonable Functions (PUFs) are the most popular FPGA-based cryptographic applications and have a broad market in lightweight IoT devices. To realize a symmetric unbiased SR latch PUF, different implementation methods that increase area consumption have been proposed. In this paper, a novel MUX-unit-based delay gate is proposed to form the M_SR PUF unit, and the output of the SR latch in the steady state is extracted as the response of the PUF. To verify the proposed M_SR PUF, it is implemented on three series of FPGAs from Xilinx Virtex-6, Virtex-7 and Kintex-7. It is worth mentioning that the symmetrical layout is relatively simple to implement through “hard macros”, which ensures better performance of PUF. The experimental results show that the proposed M_SR PUF can work stably under an ultra-wide range of environmental changes (temperature: 0°C ～80 °C; voltage: 0.8～1.2 V) with an average uniqueness of 50.125%. Furthermore, the proposed M_SR PUF unit is characterized by low overhead, consuming only 4 MUXs and 2 DFFs, and produces a high-entropy response suitable for hardware security applications.
- Hardware security /
- Physical Unclonable Functionality (PUF) /
- Symmetrical layout /
- Portability /
- Low overhead

HTML全文

图 1 传统RO PUF

下载: 全尺寸图片幻灯片

图 2 基于与非门的SR锁存器

下载: 全尺寸图片幻灯片

图 3 基于 MUX 单元的延迟门 M_NAND 设计

下载: 全尺寸图片幻灯片

图 4 提出的M_SR PUF单元

下载: 全尺寸图片幻灯片

图 5 对称比较策略

下载: 全尺寸图片幻灯片

图 6 提出的 M_SR PUF 评估系统

下载: 全尺寸图片幻灯片

图 7 22×128 bit PUF 输出序列的灰度图

下载: 全尺寸图片幻灯片

图 8 序列输出的空间特征

下载: 全尺寸图片幻灯片

图 9 Xilinx Virtex-6开发板下PUF输出序列的NIST测试

下载: 全尺寸图片幻灯片

图 10 22×128 bit PUF 输出序列的自相关测试

下载: 全尺寸图片幻灯片

图 11 3种系列 FPGA 实现的 PUF 芯片间汉明距离

下载: 全尺寸图片幻灯片

图 12 3种系类FPGA的片间汉明距离

下载: 全尺寸图片幻灯片

图 13 PUF输出响应的位翻转率

下载: 全尺寸图片幻灯片

表 1 相关PUF的性能比较

PUF 设计	FPGA平台	PUF 响应	唯一性(%)	可靠性(%)		资源消耗
PUF 设计	FPGA平台	PUF 响应	唯一性(%)	不同电压	不同温度	资源消耗
文献[8]	Spartan-3	128	49.200	80.000*		435×CLB
文献[16]	Artix	128	51.700	94.500*		–
文献[27]	Kintex-7	256	47.300	–	96.650	–
文献[27]	Artix-7	256	40.100	94.000	96.000	–
文献[9]	Spartan-3	128	46.000	>87.000		2×128 SLICEs
文献[17]	Virtex-6	128	48.438	98.242	98.326	256×CLB
本文 M_SR PUF	Virtex-6	128	50.423	94.879	97.118	4×128 MUXs 2×128 DFF
	Virtex-7		49.902	94.010	96.806
	Kintex-7		50.051	91.884	94.861
注1：*表示文献没有说明获得可靠性结果的情况. 注2：1个CLB包含2 SLICEs, 1个SLICE包含4个LUTs和8个DFFs.

下载: 导出CSV

参考文献(27)

[1]	SUNAR B, MARTIN W J, and STINSON D R. A provably secure true random number generator with built-in tolerance to active attacks[J]. IEEE Transactions on Computers, 2007, 56(1): 109–119. doi: 10.1109/TC.2007.250627
[2]	TANEJA S, RAJANNA V K, and ALIOTO M. 36.1 Unified in-memory dynamic TRNG and multi-bit static PUF entropy generation for ubiquitous hardware security[C]. Proceedings of 2021 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, USA, 2021: 498–500.
[3]	SURAGANI R, NAZARENKO E, ANAGNOSTOPOULOS N A, et al. Identification and classification of corrupted PUF responses via machine learning[C]. Proceedings of 2022 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), McLean, USA, 2022: 137–140.
[4]	KROEGER T, CHENG Wei, GUILLEY S, et al. Cross-PUF attacks on arbiter-PUFs through their power side-channel[C]. Proceedings of 2020 IEEE International Test Conference (ITC), Washington, USA, 2020: 1–5.
[5]	CHANG Zhengtai, SHI Shanshan, SONG Binwei, et al. Modeling attack resistant arbiter PUF with time-variant obfuscation scheme[C]. Proceedings of 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 2021: 60–63.
[6]	YAO Liang, LIANG Huaguo, HAN Qian, et al. M-RO PUF: A portable pure digital RO PUF based on MUX unit[J]. Microelectronics Journal, 2022, 119: 105314. doi: 10.1016/j.mejo.2021.105314
[7]	OKUMURA S, YOSHIMOTO S, KAWAGUCHI H, et al. A 128-bit chip identification generating scheme exploiting load transistors' variation in SRAM bitcells[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2012, E95.A(12): 2226–2233. doi: 10.1587/transfun.E95.A.2226
[8]	ARDAKANI A and SHOKOUHI S B. A secure and area-efficient FPGA-based SR-Latch PUF[C]. Proceedings of 2016 8th International Symposium on Telecommunications (IST), Tehran, Iran, 2016: 94–99.
[9]	YAMAMOTO D, SAKIYAMA K, IWAMOTO M, et al. Uniqueness enhancement of PUF responses based on the locations of random outputting RS latches[C]. Proceedings of the 13th International Workshop on Cryptographic Hardware and Embedded Systems, Nara, Japan, 2011: 390–496.
[10]	DANGER J L, YASHIRO R, GRABA T, et al. Analysis of mixed PUF-TRNG circuit based on SR-latches in FD-SOI technology[C]. Proceedings of the 21st Euromicro Conference on Digital System Design (DSD), Prague, Czech Republic, 2018: 508–515.
[11]	XU Xiumin, LIANG Huaguo, HUANG Zhengfeng, et al. A highly reliable butterfly PUF in SRAM-based FPGAs[J]. IEICE Electronics Express, 2017, 14(14): 20170551. doi: 10.1587/elex.14.20170551
[12]	LOTFY A, KAVEH M, MARTÍN D, et al. An efficient design of anderson PUF by utilization of the xilinx primitives in the SLICEM[J]. IEEE Access, 2021, 9: 23025–23034. doi: 10.1109/ACCESS.2021.3056291
[13]	NOZAKI Y, TAKEMOTO S, IKEZAKI Y, et al. Performance evaluation of unrolled cipher based glitch PUF implemented on virtex-7[C]. Proceedings of 2021 International Symposium on Devices, Circuits and Systems (ISDCS), Higashihiroshima, Japan, 2021: 1–4.
[14]	ZHOU Kai, LIANG Huaguo, JIANG Yue, et al. FPGA-based RO PUF with low overhead and high stability[J]. Electronics Letters, 2019, 55(9): 510–513. doi: 10.1049/el.2019.0451
[15]	CUI Yijun, CHEN Yunpeng, WANG Chenghua, et al. Programmable ring oscillator PUF based on switch matrix[C]. Proceedings of 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 2020: 1–4.
[16]	ZHOU Ting, JI Yuxin, CHEN Mingyi, et al. PL-MRO PUF: High speed pseudo-LFSR PUF based on multiple ring oscillators[C]. Proceedings of 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 2020: 1–5.
[17]	YAO Liang, LIANG Huaguo, HUANG Zhengfeng, et al. A lightweight configurable XOR RO-PUF design based on xilinx FPGA[C]. Proceedings of 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 2021: 83–88.
[18]	YAMAMOTO D, SAKIYAMA K, IWAMOTO M, et al. Variety enhancement of PUF responses using the locations of random outputting RS latches[J]. Journal of Cryptographic Engineering, 2013, 3(4): 197–211. doi: 10.1007/s13389-012-0044-0
[19]	CHALLA R P, ISLAM S A, and KATKOORI S. An SR flip-flop based physical unclonable functions for hardware security[C]. Proceedings of the 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, USA, 2019: 574–577.
[20]	WANG Jiadong, CUI Aijiao, LI Mengyang, et al. An ultra-low overhead LUT-based PUF for FPGA[C]. Proceedings of 2016 IEEE Asian Hardware-oriented Security and Trust, Yilan, China, 2016: 1–6.
[21]	孙子文, 叶乔. 利用震荡环频率特性提取多位可靠信息熵的物理不可克隆函数研究[J]. 电子与信息学报, 2021, 43(1): 234–241. doi: 10.11999/JEIT191013 SUN Ziwen and YE Qiao. Study on the physical unclonable function of the reliable information entropy extracted by the frequency characteristic of oscillating ring[J]. Journal of Electronics &Information Technology, 2021, 43(1): 234–241. doi: 10.11999/JEIT191013
[22]	HATA H and ICHIKAWA S. FPGA implementation of metastability-based true random number generator[J]. IEICE Transactions on Information and Systems, 2012, E95.D(2): 426–436. doi: 10.1587/transinf.E95.D.426
[23]	XILINX Corporation. 7 series FPGAs configurable logic block user guide[EB/OL]. https://www.xilinx.com/content/dam/xilinx/support/documentation/user_guides/ug474_7Series_CLB.pdf, 2020.
[24]	GE Lulu and PARHI K K. Molecular MUX-based physical unclonable functions[C]. Proceedings of 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 2020: 482–487.
[25]	RAMANUJAM S and BURLESON W. Reconfiguring the mux-based arbiter PUF using FeFETs[C]. Proceedings of the 22nd International Symposium on Quality Electronic Design (ISQED), Santa Clara, USA, 2021: 257–262.
[26]	RUKHIN A, SOTO J, NECHVATAL J, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications[R]. NIST Special Publication 800-220, 2001.
[27]	CUI Yijun, GU Chongyan, MA Qingqing, et al. Lightweight modeling attack-resistant multiplexer-based multi-PUF (MMPUF) design on FPGA[J]. Electronics, 2020, 9(5): 815. doi: 10.3390/electronics9050815