Adaptive Rao Detection of Radar Targets Based on the Priori-Knowledge of Sea Clutter
-
摘要: 针对非高斯非均匀海杂波背景下雷达海面目标检测性能改善的问题，该文基于海杂波的先验知识提出了一种自适应Rao雷达目标检测方法。首先将海杂波的纹理分量和散斑协方差矩阵分别建模为逆高斯随机变量和逆复Wishart分布的随机矩阵，然后基于Rao检验和未知参数估计，设计了一种匹配海杂波特性的雷达目标自适应Rao检测方法。通过理论推导和实验验证了所提检测方法对杂波平均功率和协方差均值矩阵具有恒虚警特性。仿真数据和实测数据实验结果表明，在非高斯非均匀环境下所提检测方法优于已有检测方法，并且具有良好的鲁棒性。Abstract: An adaptive Rao detection method for radar targets is proposed based on the priori knowledge of sea clutter to improve the radar’s target detection performance in non-Gaussian and nonhomogeneous sea clutter. First, the texture component and the speckle covariance matrix of sea clutter are modeled as an inverse Gaussian random variable and an inverse complex Wishart random matrix, respectively. Then, an adaptive Rao detection method for radar targets, with quite similar characteristics as sea clutter, is designed based on the Rao test and unknown parameter estimation. The detection method is verified by theoretical derivation and experiments in demonstrating constant false alarm characteristics for the mean power and covariance mean matrix of sea clutter. The experimental results of the simulated and experimental data reveal that the proposed detection method outperforms existing detection methods in non-Gaussian and nonhomogeneous sea clutter environments with good robustness.
-
Key words:
- Radar targets /
- Adaptive Rao detection /
- Sea clutter /
- Priori knowledge
-
[1] 刘宁波, 姜星宇, 丁昊, 等. 雷达大擦地角海杂波特性与目标检测研究综述[J]. 电子与信息学报, 2021, 43(10): 2771–2780. doi: 10.11999/JEIT200451LIU Ningbo, JIANG Xingyu, DING Hao, et al. Summary of research on characteristics of radar sea clutter and target detection at high grazing angles[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2771–2780. doi: 10.11999/JEIT200451 [2] BANDIERA F, ORLANDO D, and RICCI G. Advanced Radar Detection Schemes Under Mismatched Signal Models[M]. Cham: Springer, 2009: 1–105. [3] LIU Jun, HAN Jinwang, ZHANG Zijing, et al. Bayesian detection for MIMO radar in Gaussian clutter[J]. IEEE Transactions on Signal Processing, 2018, 66(24): 6549–6559. doi: 10.1109/TSP.2018.2879038 [4] KELLY E J. An adaptive detection algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, AES-22(2): 115–127. doi: 10.1109/TAES.1986.310745 [5] ROBEY F C, FUHRMANN D R, KELLY E J, et al. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208–216. doi: 10.1109/7.135446 [6] WARD K D. Compound representation of high resolution sea clutter[J]. Electronics Letters, 1981, 17(16): 561–563. doi: 10.1049/el:19810394 [7] WATTS S. Radar detection prediction in sea clutter using the compound K-distribution model[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1985, 132(7): 613–620. doi: 10.1049/ip-f-1.1985.0115 [8] MEZACHE A, SOLTANI F, SAHED M, et al. Model for non-Rayleigh clutter amplitudes using compound inverse Gaussian distribution: An experimental analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 142–153. doi: 10.1109/TAES.2014.130332 [9] 水鹏朗, 田超, 封天. 逆高斯纹理复合高斯杂波对异常样本稳健的三分位点估计方法[J]. 电子与信息学报, 待发表.S H U I P e n g l a n g , T I A N C h a o , a n d F E N G T i a n . O u t l i e r - r o b u s t t r i - p e r c e n t i l e p a r a m e t e r e s t i m a t i o n m e t h o d o f c o m p o u n d - G a u s s i a n c l u t t e r w i t h i n v e r s e G a u s s i a n t e x t u r e s [ J ] . < i > J o u r n a l < / i > < i > o f < / i > < i > E l e c t r o n i c s < / i > & a m p ; < i > I n f o r m a t i o n < / i > < i > T e c h n o l o g y < / i > , T o b e p u b l i s h . d o i : [10] SHUI Penglang, ZOU Pengjia, and FENG Tian. Outlier-robust truncated maximum likelihood parameter estimators of generalized Pareto distributions[J]. Digital Signal Processing, 2022, 127: 103527. doi: 10.1016/j.dsp.2022.103527 [11] FENG Tian and SHUI Penglang. Outlier-robust tri-percentile parameter estimation of compound-Gaussian clutter with lognormal distributed texture[J]. Digital Signal Processing, 2022, 120: 103307. doi: 10.1016/j.dsp.2021.103307 [12] KONG Lingjiang, LI Na, CUI Guolong, et al. Adaptive Bayesian detection for multiple-input multiple-output radar in compound-Gaussian clutter with random texture[J]. IET Radar, Sonar & Navigation, 2016, 10(4): 689–698. doi: 10.1049/iet-rsn.2015.0241 [13] 韩金旺, 张子敬, 刘军, 等. 基于贝叶斯的高斯杂波背景下MIMO雷达自适应检测算法[J]. 雷达学报, 2019, 8(4): 501–509. doi: 10.12000/JR18090HAN Jinwang, ZHANG Zijing, LIU Jun, et al. Adaptive Bayesian detection for MIMO radar in Gaussian clutter[J]. Journal of Radars, 2019, 8(4): 501–509. doi: 10.12000/JR18090 [14] XUE Jian, XU Shuwen, LIU Jun, et al. Bayesian detection for radar targets in compound-Gaussian sea clutter[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4020805. doi: 10.1109/LGRS.2022.3140727 [15] OLLILA E, TYLER D E, KOIVUNEN V, et al. Compound-Gaussian clutter modeling with an inverse Gaussian texture distribution[J]. IEEE Signal Processing Letters, 2012, 19(12): 876–879. doi: 10.1109/LSP.2012.2221698 [16] SUN Mengru, LIU Weijian, LIU Jun, et al. Complex parameter Rao, Wald, gradient, and Durbin tests for multichannel signal detection[J]. IEEE Transactions on Signal Processing, 2022, 70: 117–131. doi: 10.1109/TSP.2021.3132485 [17] LIU Weijian, ZHANG Zhaojian, LIU Jun, et al. Detection of a rank-one signal with limited training data[J]. Signal Processing, 2021, 186: 108120. doi: 10.1016/j.sigpro.2021.108120 [18] SHUI Penglang, SHI Lixiang, YU Han, et al. Iterative maximum likelihood and outlier-robust bipercentile estimation of parameters of compound-Gaussian clutter with inverse Gaussian texture[J]. IEEE Signal Processing Letters, 2016, 23(11): 1572–1576. doi: 10.1109/LSP.2016.2605129 [19] SVENSSON L and LUNDBERG M. On posterior distributions for signals in Gaussian noise with unknown covariance matrix[J]. IEEE Transactions on Signal Processing, 2005, 53(9): 3554–3571. doi: 10.1109/TSP.2005.853102 [20] TAGUE J A and CALDWELL C I. Expectations of useful complex Wishart forms[J]. Multidimensional Systems and Signal Processing, 1994, 5(3): 263–279. doi: 10.1007/BF00980709 [21] 许述文, 王喆祥, 水鹏朗. 海杂波背景下雷达目标贝叶斯检测算法[J]. 西安电子科技大学学报, 2021, 48(2): 15–26. doi: 10.19665/j.issn1001-2400.2021.02.003XU Shuwen, WANG Zhexiang, and SHUI Penglang. Knowledge-based adaptive detection of radar targets in sea clutter background[J]. Journal of Xidian University, 2021, 48(2): 15–26. doi: 10.19665/j.issn1001-2400.2021.02.003 [22] CONTE E, LOPS M, and RICCI G. Asymptotically optimum radar detection in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 617–625. doi: 10.1109/7.381910 [23] XUE Jian, XU Shuwen, and SHUI Penglang. Knowledge-based target detection in compound Gaussian clutter with inverse Gaussian texture[J]. Digital Signal Processing, 2019, 95: 102590. 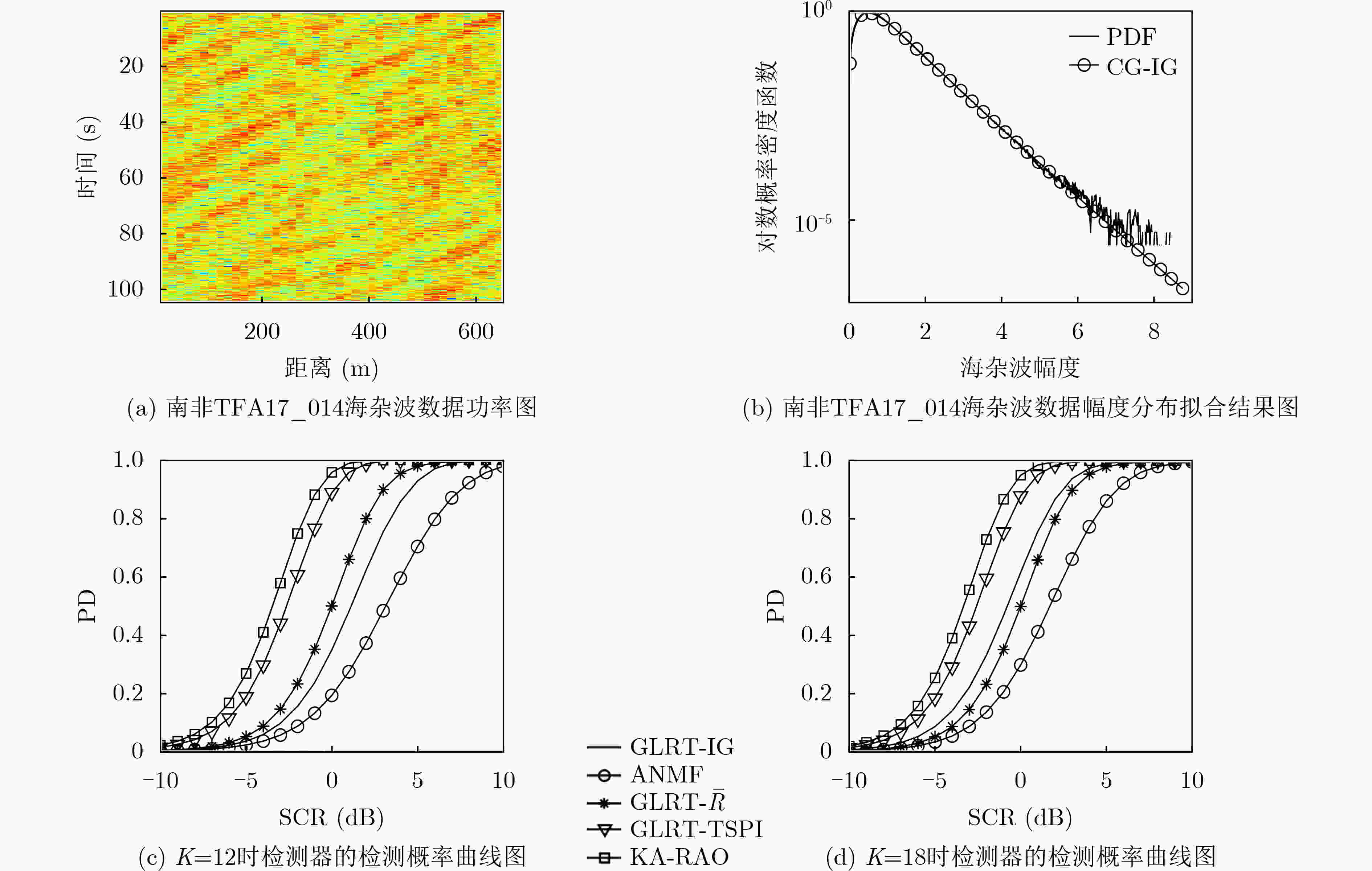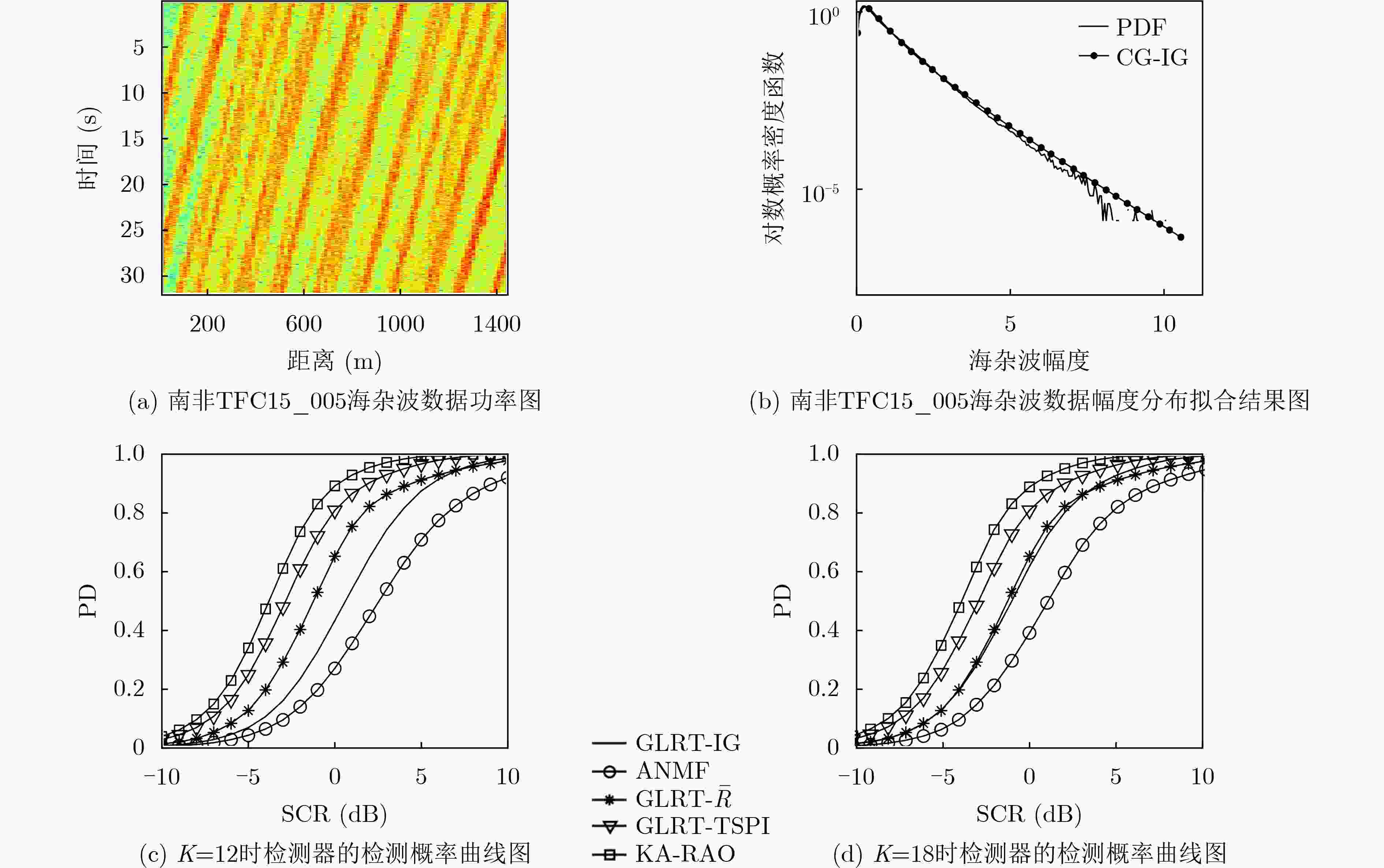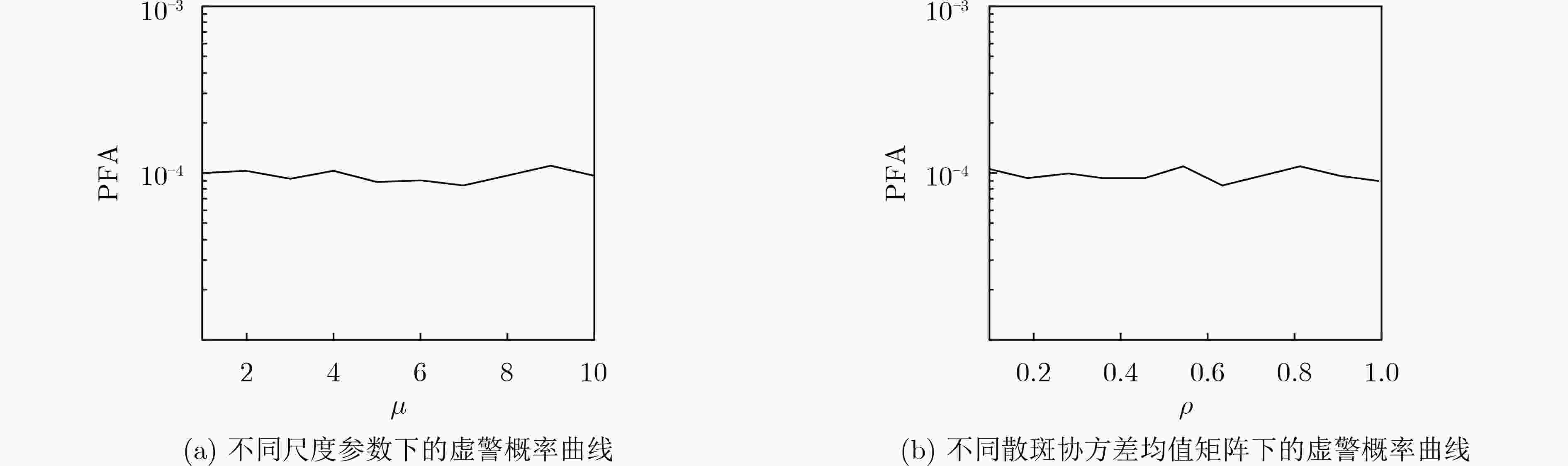doi: 10.1016/j.dsp.2019.102590 [24] HERSELMAN P L and BAKER C J. Analysis of calibrated sea clutter and boat reflectivity data at C- and X-band in South African coastal waters[C]. Proceedings of the IET International Conference on Radar Systems 2007, Edinburgh, UK, 2007: 1–5. -
下载:
图(7)
计量
- 文章访问数: 753
- HTML全文浏览量: 249
- PDF下载量: 162
- 被引次数: 0
下载:
