基于辅助变量增强的可逆彩色图像灰度化

廖一帆; 李子豪; 伍春花; 汪国有; 刘且根

doi:10.11999/JEIT221205

基于辅助变量增强的可逆彩色图像灰度化

doi: 10.11999/JEIT221205

1.
南昌大学信息工程学院南昌 330031
2.
华中科技大学人工智能与自动化学院武汉 430000

基金项目: 国家优秀青年科学基金(62122033)，江西省重点研发计划(20212BBE53001)

详细信息

作者简介:
廖一帆：女，博士，主要研究方向为计算机视觉与图像处理

李子豪：男，硕士，主要研究方向为图像重建、计算机视觉与图像处理

伍春花：女，硕士，主要研究方向为计算成像、计算机视觉与图像处理

汪国有：男，教授，主要研究方向为字典学习、压缩感知、计算机视觉与图像处理

刘且根：男，教授，主要研究方向为字典学习、压缩感知、计算机视觉与图像处理

通讯作者:
刘且根　liuqiegen@ncu.edu.cn

中图分类号: TN911; TP751
计量
- 文章访问数: 415
- HTML全文浏览量: 314
- PDF下载量: 108
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-15
- 修回日期: 2023-04-12
- 网络出版日期: 2023-04-17
- 刊出日期: 2023-12-26

Invertible Color Image Decolorization Based on Variable Augmented Network

1.
School of Information Engineering, Nanchang University, Nanchang 330031, China
2.
School of Artificial Intelligence and Automation, Huazhong University of Science and Technology, Wuhan 430000, China

Funds: The National Science Fund for Outstanding Young Scholars (62122033), The Key Research and Development Program of Jiangxi Province (20212BBE53001)

摘要

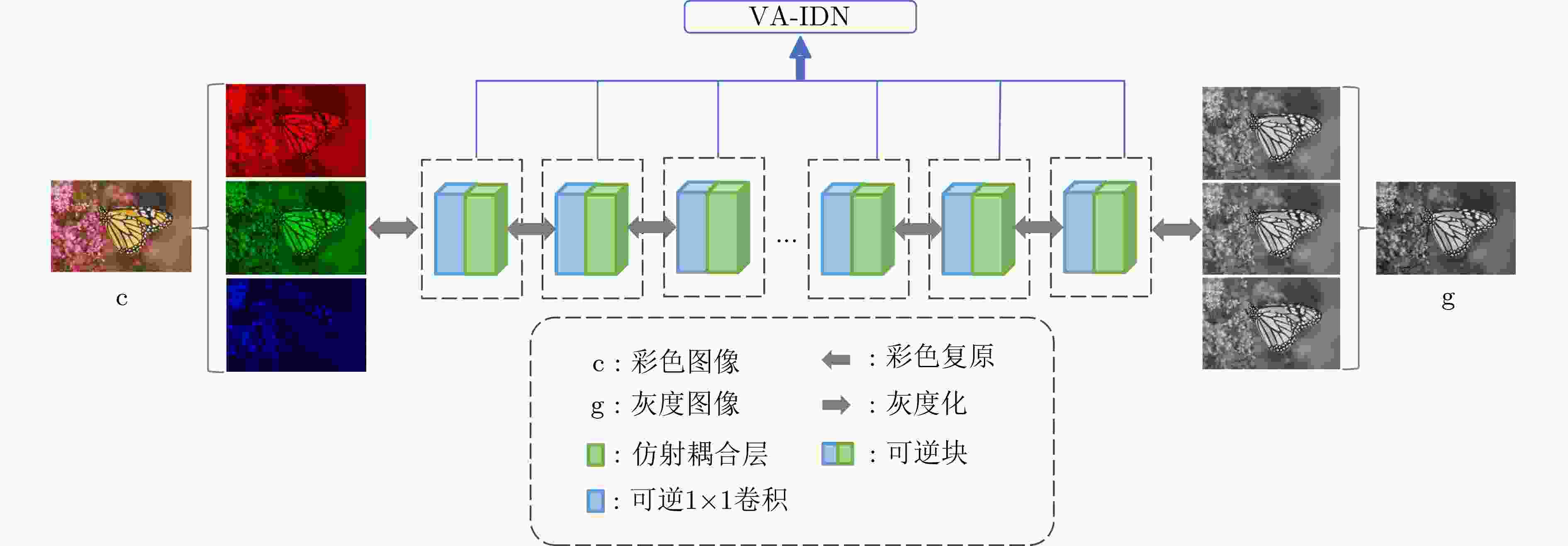
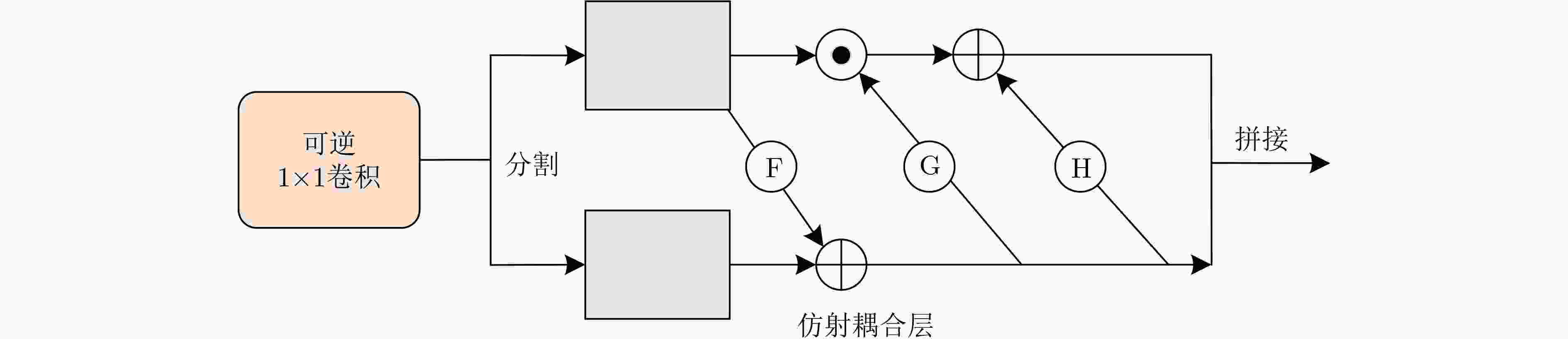
摘要: 彩色图像灰度化是一种被广泛应用于各个领域的图像压缩方式，但很少有研究关注彩色图像与灰度图像之间的相互转换技术。该文运用深度学习，创新性地提出了一种基于辅助变量增强的可逆彩色图像灰度化方法。该方法使用变量增强技术来保证输出与输入变量通道数相同以满足网络的可逆特性。具体来说，该方法通过可逆神经网络的正向过程实现彩色图像灰度化，逆向过程实现灰度图像的色彩复原。将所提方法在VOC2012, NCD和Wallpaper数据集上进行定性和定量比较。实验结果表明，所提方法在评价指标上均获得了更好的结果。无论是在全局还是局部，生成图像都可以最大程度地保留亮度、颜色对比度和结构相关性等特征。
- 彩色图像灰度化 /
- 可逆神经网络 /
- 变量增强 /
- 色彩复原
Abstract: Decolorization is an image compression method widely used in various fields, but few researches focus on the mutual conversion technology of color image and grayscale image. In this paper, a deep learning method is used to propose innovatively an invertible decolorization method based on variable augmentation. This method uses variable augmentation technology to ensure that the output has the same number of channels as the input variable, which satisfies the reversible characteristics of the network. Specifically, the proposed method realizes the decolorization through the forward process of the invertible neural network, and realizes the color restoration of grayscale images through the reverse process. The proposed method performs qualitative and quantitative comparisons on VOC2012, NCD, Wallpaper datasets. The experimental results show that the proposed method achieves better results in the evaluation indicators. The quality of the generated images can preserve the characteristics of brightness, color contrast and structural correlation to the greatest extent, both globally and locally.
- Color-to-gray conversion /
- Invertible neural network /
- Variable augmentation /
- Color restoration

HTML全文

图 1 基于辅助变量增强的可逆彩色图像灰度化模型的可视化结构图

下载: 全尺寸图片幻灯片

图 2 可逆块的详细结构图

下载: 全尺寸图片幻灯片

图 3 不同算法在不同数据集上图像灰度化效果

下载: 全尺寸图片幻灯片

图 4 原始彩色图像中细节放大图的灰度化结果

下载: 全尺寸图片幻灯片

图 5 原始彩色图像中细节放大图的色彩复原结果

下载: 全尺寸图片幻灯片

表 1 Wallpaper数据集的CCPR, CCFR和E-score结果

τ	CCPR			CCFR			E-score
τ	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN
1	0.9578	0.9638	0.9555	0.9275	0.9294	0.9729	0.9418	0.9456	0.9637
2	0.9281	0.9361	0.9218	0.8850	0.8885	0.9634	0.9048	0.9105	0.9414
3	0.9065	0.9151	0.8973	0.8648	0.8687	0.9586	0.8840	0.8902	0.9261
4	0.8863	0.8951	0.8743	0.8556	0.8595	0.9555	0.8694	0.8759	0.9122
5	0.8685	0.8773	0.8538	0.8503	0.8547	0.9536	0.8581	0.8649	0.9000
6	0.8515	0.8601	0.8346	0.8480	0.8517	0.9518	0.8484	0.8550	0.8884
7	0.8352	0.8437	0.8160	0.8462	0.8495	0.9499	0.8393	0.8457	0.8768
8	0.8197	0.8279	0.7979	0.8455	0.8490	0.9479	0.8310	0.8375	0.8654
9	0.8044	0.8124	0.7805	0.8458	0.8489	0.9456	0.8232	0.8294	0.8539
10	0.7894	0.7971	0.7633	0.8461	0.8485	0.9440	0.8154	0.8212	0.8428

下载: 导出CSV

表 2 VOC2012数据集的CCPR, CCFR和E-score结果

τ	CCPR			CCFR			E-score
τ	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN
1	0.9687	0.9710	0.9683	0.9382	0.9378	0.9708	0.9531	0.9539	0.9695
2	0.9404	0.9446	0.9404	0.8640	0.8630	0.9557	0.9002	0.9016	0.9479
3	0.9185	0.9244	0.9195	0.8130	0.8113	0.9518	0.8621	0.8637	0.9352
4	0.8972	0.9052	0.8989	0.7835	0.7812	0.9530	0.8360	0.8381	0.9249
5	0.8788	0.8887	0.8810	0.7667	0.7639	0.9546	0.8183	0.8209	0.9159
6	0.8617	0.8736	0.8642	0.7589	0.7551	0.9558	0.8062	0.8092	0.9072
7	0.8458	0.8595	0.8483	0.7560	0.7516	0.9580	0.7973	0.8009	0.8992
8	0.8308	0.8461	0.8334	0.7563	0.7512	0.9597	0.7906	0.7947	0.8913
9	0.8166	0.8333	0.8191	0.7589	0.7529	0.9609	0.7853	0.7898	0.8833
10	0.8031	0.8211	0.8055	0.7628	0.7568	0.9620	0.7809	0.7863	0.8755

下载: 导出CSV

表 3 NCD数据集的CCPR, CCFR和E-score结果

τ	CCPR			CCFR			E-score
τ	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN	Gcs	Ledecolor	VA-IDN
1	0.9503	0.9587	0.9451	0.9466	0.9389	0.9716	0.9480	0.9483	0.9579
2	0.9493	0.9581	0.9431	0.9184	0.8976	0.9644	0.9327	0.9261	0.9533
3	0.9471	0.9568	0.9431	0.9010	0.8729	0.9611	0.9223	0.9119	0.9516
4	0.9424	0.9535	0.9399	0.8925	0.8572	0.9604	0.9153	0.9015	0.9496
5	0.9376	0.9507	0.9362	0.8883	0.8481	0.9612	0.9104	0.8948	0.9480
6	0.9317	0.9477	0.9311	0.8867	0.8429	0.9619	0.9064	0.8903	0.9456
7	0.9252	0.9450	0.9251	0.8887	0.8405	0.9625	0.9040	0.8876	0.9427
8	0.9203	0.9432	0.9205	0.8900	0.8398	0.9630	0.9020	0.8862	0.9403
9	0.9131	0.9410	0.9127	0.8936	0.8407	0.9637	0.8999	0.8856	0.9362
10	0.9058	0.9390	0.9039	0.8971	0.8426	0.9645	0.8977	0.8856	0.9315

下载: 导出CSV

表 4 彩色图像灰度化的PSNR和SSIM值

数据指标	VOC2012		Wallpaper		NCD
数据指标	IDN	VA-IDN	IDN	VA-IDN	IDN	VA-IDN
PSNR (dB)	40.660	45.648	34.969	37.781	43.611	45.639
SSIM	0.9790	0.9982	0.9092	0.9913	0.9791	0.9988

下载: 导出CSV

表 5 灰度图像色彩复原的PSNR和SSIM值

数据指标	VOC2012		Wallpaper		NCD
数据指标	IDN	VA-IDN	IDN	VA-IDN	IDN	VA-IDN
PSNR (dB)	39.505	64.759	35.068	64.696	42.245	45.777
SSIM	0.9868	0.9998	0.9553	0.9998	0.9884	0.9969

下载: 导出CSV

参考文献(22)

[1]	LIU Qiegen, XIONG Jiaojiao, LI Zhu, et al. Extended RGB2Gray conversion model for efficient contrast preserving decolorization[J]. Multimedia Tools and Applications, 2017, 76(12): 14055–14074. doi: 10.1007/s11042-016-3748-9
[2]	ZHANG Lina and YI Wan. Color-to-gray conversion based on boundary points[C]. 11th International Conference on Communications, Circuits and Systems, Chengdu, China, 2022: 241–245.
[3]	LIU Qiegen, LI Sanqian, XIONG Jiaojiao, et al. WpmDecolor: Weighted projection maximum solver for contrast-preserving decolorization[J]. The Visual Computer, 2019, 35(2): 205–221. doi: 10.1007/s00371-017-1464-8
[4]	朱波, 汶德胜, 王飞, 等. 应用字典学习算法改善Bayer格式图像彩色恢复效果[J]. 电子与信息学报, 2013, 35(4): 812–819. doi: 10.3724/SP.J.1146.2012.00947 ZHU Bo, WEN Desheng, WANG Fei, et al. Improvement of Bayer-pattern demosaicking with dictionary learning algorithm[J]. Journal of Electronics &Information Technology, 2013, 35(4): 812–819. doi: 10.3724/SP.J.1146.2012.00947
[5]	ZHU Wen, HU Ruizhen, and LIU Ligang. Grey conversion via perceived-contrast[J]. The Visual Computer, 2014, 30(3): 299–309. doi: 10.1007/s00371-013-0854-9
[6]	卢红阳, 刘且根, 熊娇娇, 等. 基于最大加权投影求解的彩色图像灰度化对比度保留算法[J]. 自动化学报, 2017, 43(5): 843–854. doi: 10.16383/j.aas.2017.c160077 LU Hongyang, LIU Qiegen, XIONG Jiaojiao, et al. Maximum weighted projection solver for contrast preserving decolorization[J]. Acta Automatica Sinica, 2017, 43(5): 843–854. doi: 10.16383/j.aas.2017.c160077
[7]	LU Cewu, XU Li, and JIA Jiaya. Contrast preserving decolorization[C]. 2012 IEEE International Conference on Computational Photography, Seattle, USA, 2012: 1–7.
[8]	LU Cewu, XU Li, and JIA Jiaya. Real-time contrast preserving decolorization[C]. SIGGRAPH Asia 2012 Technical Briefs, Singapore, 2012: 34.
[9]	LIU Qiegen, LIU P X, WANG Yuhao, et al. Semiparametric decolorization with Laplacian-based perceptual quality metric[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2017, 27(9): 1856–1868. doi: 10.1109/TCSVT.2016.2555779
[10]	HSIN C, LE H N, and SHIN S J. Color to grayscale transform preserving natural order of hues[C]. Proceedings of 2011 International Conference on Electrical Engineering and Informatics, Bandung, Indonesia, 2011: 1–6.
[11]	ANCUTI C and ANCUTI C O. Laplacian-guided image decolorization[C]. 2016 IEEE International Conference on Image Processing, Phoenix, USA, 2016: 4107–4111.
[12]	AN Jiancheng, KPEYITON K G, and SHI Qingnan. Grayscale images colorization with convolutional neural networks[J]. Soft Computing, 2020, 24(7): 4751–4758. doi: 10.1007/s00500-020-04711-3
[13]	DU Kangning, LIU Changtong, CAO Lin, et al. Double-channel guided generative adversarial network for image colorization[J]. IEEE Access, 2021, 9: 21604–21617. doi: 10.1109/ACCESS.2021.3055575
[14]	VITORIA P, RAAD L, and BALLESTER C. ChromaGAN: Adversarial picture colorization with semantic class distribution[C]. Proceedings of 2020 IEEE Winter Conference on Applications of Computer Vision, Snowmass, USA, 2020: 2434–2443.
[15]	XIA Menghan, LIU Xueting, and WONG T T. Invertible grayscale[J]. ACM Transactions on Graphics, 2018, 37(6): 246. doi: 10.1145/3272127.3275080
[16]	ZHAO Rui, LIU Tianshan, XIAO Jun, et al. Invertible image decolorization[J]. IEEE Transactions on Image Processing, 2021, 30: 6081–6095. doi: 10.1109/TIP.2021.3091902
[17]	LIU Qiegen and LEUNG H. Variable augmented neural network for decolorization and multi-exposure fusion[J]. Information Fusion, 2019, 46: 114–127. doi: 10.1016/j.inffus.2018.05.007
[18]	XING Yazhou, QIAN Zian, and CHEN Qifeng. Invertible image signal processing[C]. Proceedings of 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 6283–6292.
[19]	XIAO Mingqing, ZHENG Shuxin, LIU Chang, et al. Invertible image rescaling[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 126–144.
[20]	KINGMA D P and DHARIWAL P. Glow: Generative flow with invertible 1x1 convolutions[C]. Proceedings of International Conference on Neural Information Processing Systems 2018, Montréal, Canada, 2018: 10236-10245.
[21]	LIU Qiegen, LIU P X, XIE Weisi, et al. GcsDecolor: Gradient correlation similarity for efficient contrast preserving decolorization[J]. IEEE Transactions on Image Processing, 2015, 24(9): 2889–2904. doi: 10.1109/TIP.2015.2423615
[22]	LIU Qiegen, Shao Guangpu, WANG Yuhao, et al. Log-Euclidean metrics for contrast preserving decolorization[J]. IEEE Transactions on Image Processing, 2017, 26(12): 5772–5783. doi: 10.1109/TIP.2017.2745104