A Lattice Cipher Template Attack Method Based on Recurrent Cryptography
-
摘要: 该文分析了格密码解封装过程存在的能量泄露,针对消息解码操作提出一种基于模板与密文循环特性的消息恢复方法,该方法采用汉明重量模型与归一化类间方差(NICV)方法对解码字节的中间更新状态构建模板,并利用密文循环特性构造特殊密文,结合算法运算过程中产生的能量泄露,实现了对格密码中秘密消息和共享密钥的恢复。该文以Saber算法及其变体为例对提出的攻击方法在ChipWhisperer平台上进行了验证,结果表明,该攻击方法可以成功还原封装阶段的秘密消息和共享密钥,在预处理阶段仅需900条能量迹即可完成对模板的构建,共需要32条能量迹完成秘密消息的恢复。在未增加信噪比(SNR)条件下,消息恢复成功率达到66.7%,而在合适信噪比条件下,消息恢复成功率达到98.43%。Abstract: The energy leakage in the decapsulation process of lattice-based cryptography is analyzed and a message recovery method targeting the message decoding with profiling and ciphertexts rotation is proposed in this paper. The templates are constructed using Hamming weight model as well as Normalized Inter-Class Variance (NICV) for the intermediate state of decoded bytes. The special ciphertexts are built by rotating the original ciphertexts. Combining the energy leakage generated during the calculations, the secret messages and shared keys are recovered. Experiments and tests are carried out with Saber and its variants on the ChipWhisperer-STM32F303 board and the results indicate that the proposed method can successfully recover the secret message and shared key of the encapsulation stage. It only needs 900 energy traces to complete the construction for templates and a total of 32 power traces in recovering the secret message. The success rate of message recovery reaches 66.7% under the condition of no increasing the Signal-to-Noise Ratio (SNR), and 98.43% under the condition of sufficient SNR.
-
Key words:
- Lattice-based cryptography /
- Energy leakage /
- Template analysis /
- Ciphertexts rotation /
- Saber algorithm
-
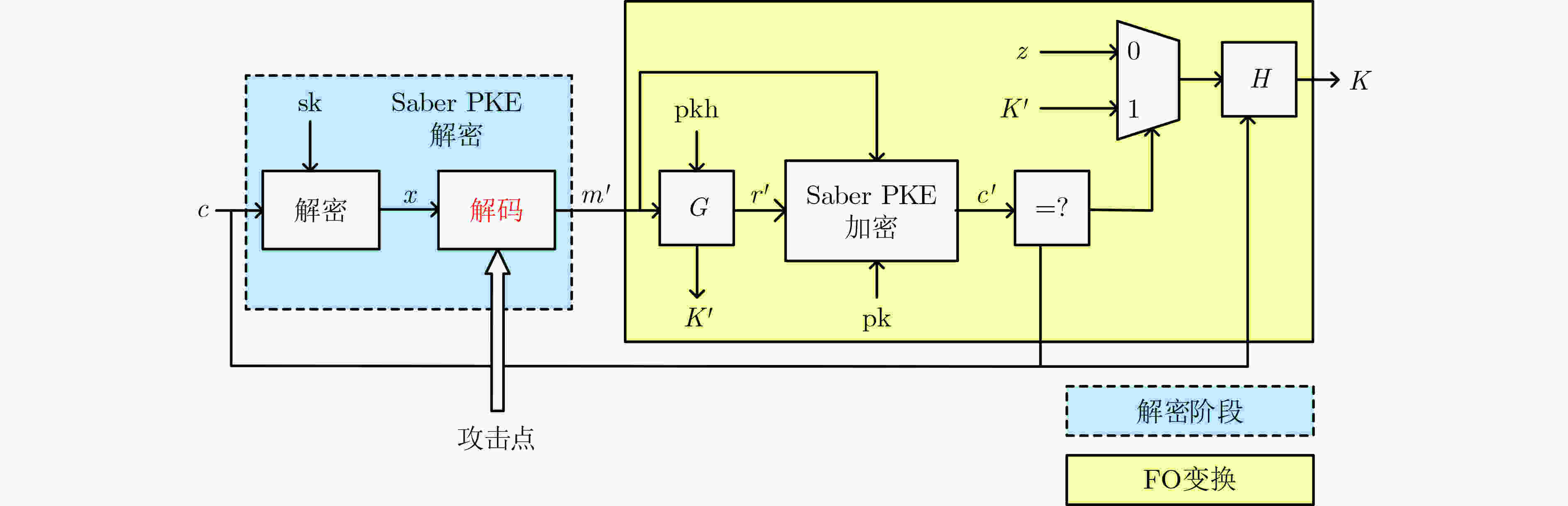
算法1 Saber PKE解密算法 输入:私钥$ s \in {B^*} $ 密文$c = ({c_m},{\boldsymbol{b}}') \in {B^{\text{*} } }$ 输出:解密消息$ m' \in {B^{32}} $ (1) $v = {\boldsymbol{b}}{'^{\rm{T} } }(s\text{mod} p) \in {R_p}$ (2) $ m' = ((v + {h_2} - {2^{{\varepsilon _p} - {\varepsilon _T}}}{c_m})\text{mod} p) > > ({\varepsilon _p} - 1) \in {R_2} $ (3) 返回$ m' $ 算法2 Saber KEM解封装算法 输入:私钥${{\rm{sk}}_{{\rm{KEM}}} } = (z,{\rm{pkh,pk}},s) \in {B^{\text{*} } }$ 密文$ c \in {B^{\text{*}}} $ 输出:共享密钥$ K \in {B^{32}} $ (1) $m' = {\rm{Saber}}\; {\rm{PKE.Dec}}(s,c)$ (2) $(K',r') = G({\rm{pkh}},m')$ (3) $c' = {\rm{Saber} }\; {\rm{PKE.Enc} }({\rm{pk}},m';r')$ (4) 若 $ c = c' $ 则返回$K = {\rm{KDF}}(K'||H(c))$ (5) 否则返回$K = {\rm{KDF}}(z||H(c))$ 算法3 Saber POLmsg2BS (1) void POLmsg2BS(uint8_t bytes[SABER_KEYBYTES],
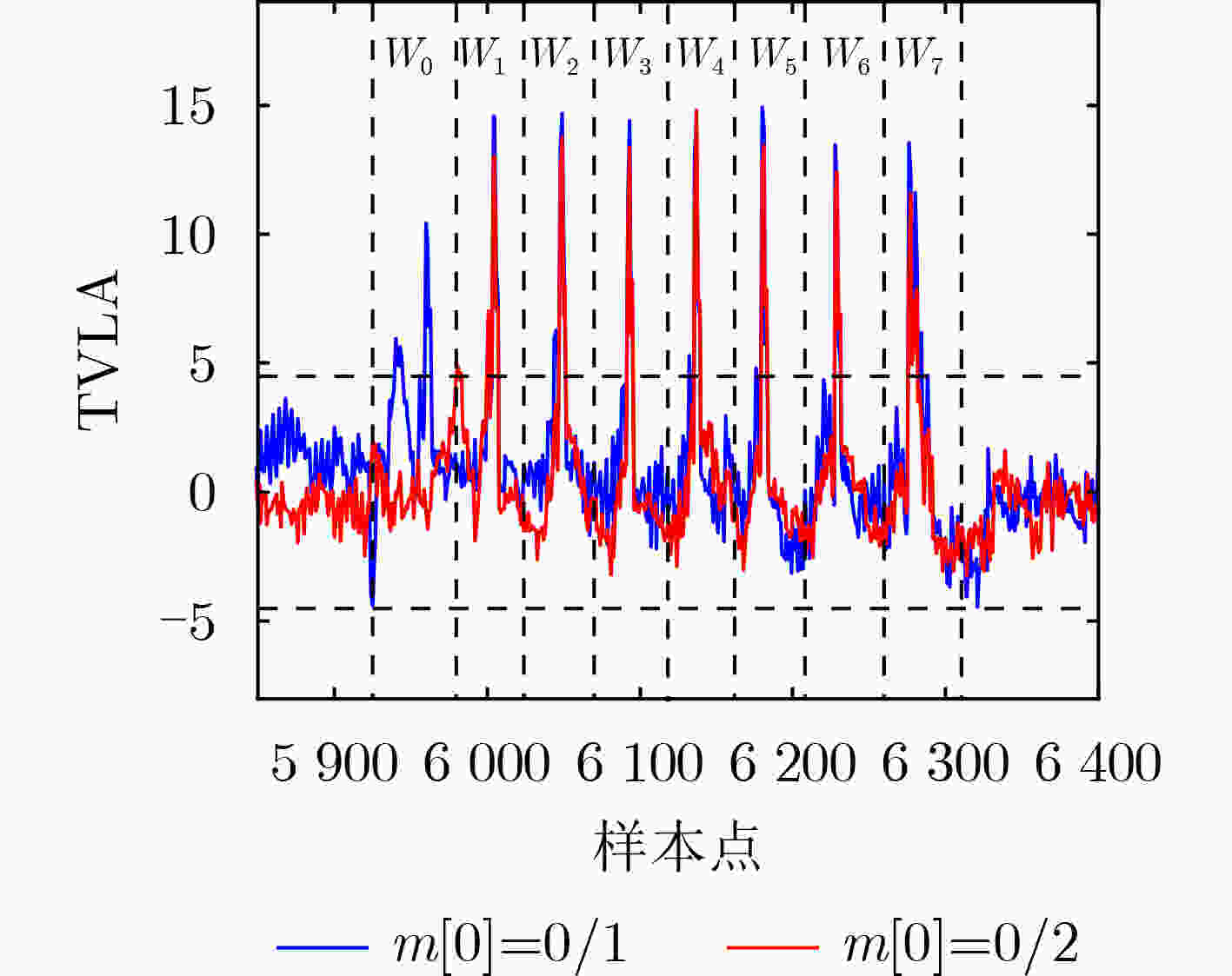
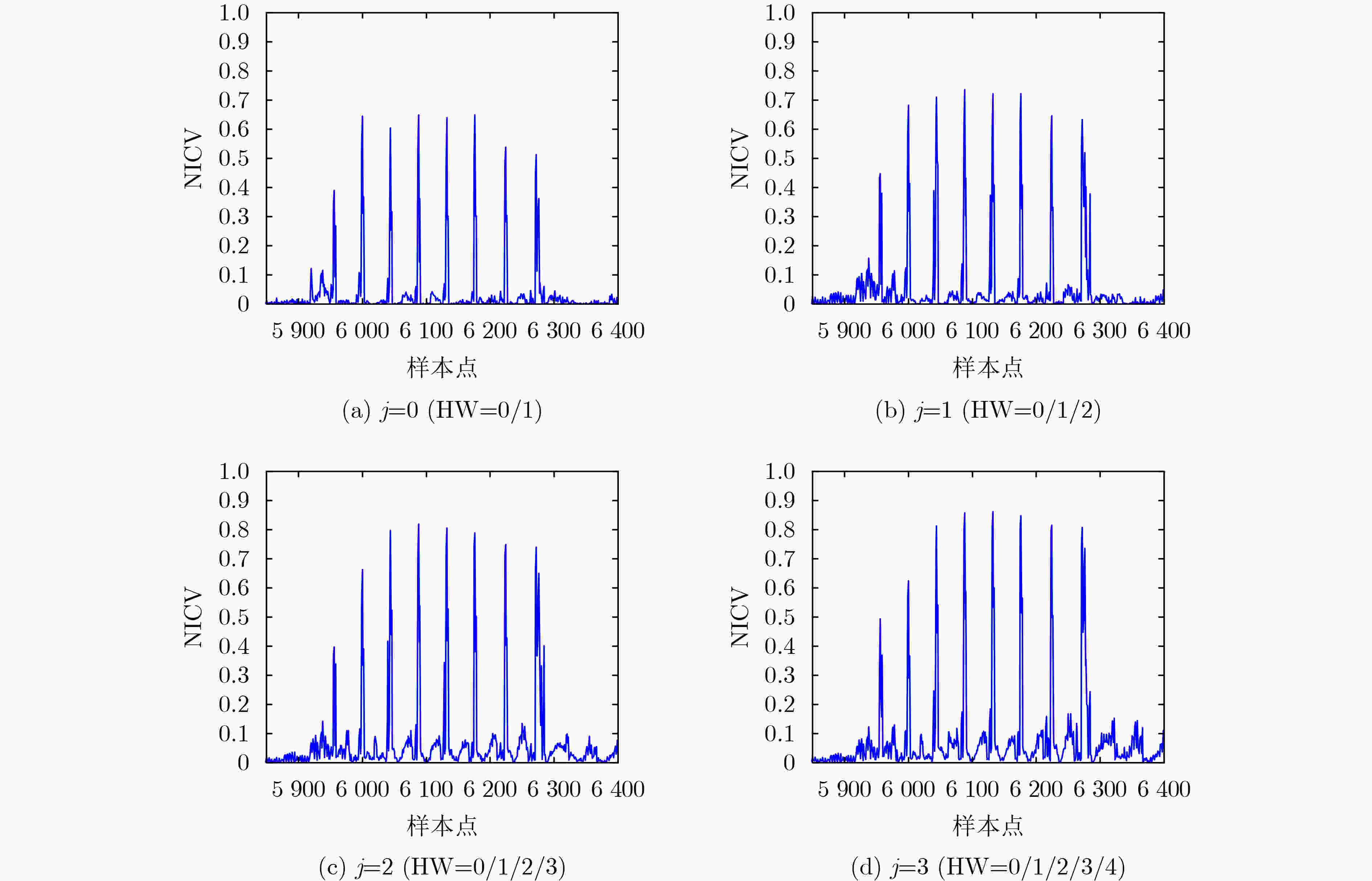
const poly *data) {(2) size_t t, i, j; (3) for (j = 0; j < SABER_KEYBYTES; j++) { (4) bytes[j] = 0; (5) for (i = 0; i < 8; i++) { (6) t = (data->coeffs[j × 8 + i] & 0x01); (7) bytes[j] |= t << i; (8) } (9) } (10) } 算法4 针对Saber算法的消息恢复方法 预处理阶段 (1) for j from 0 by 1 to 7 do (2) for k from 0 by 1 to j+1 do (3) $T_{\left( {0,j} \right)}^k = {{\rm{Saber}}} {{\rm{KEM}}} .{\rm{Dec}}({\rm{CT}}_{\left( {0,j} \right)}^k)$ (4) end for (5) ${W_j} = {{\rm{TVLA}}} (T_{(0,1)}^0,T_{\left( {0,1} \right)}^1)$ (6) ${P_{(0,j)} } = {\rm{NICV}}({W_j},T_{\left( {0,j} \right)}^0,\cdots,T_{\left( {0,j} \right)}^{j + 1})$ (7) for k from 0 by 1 to j+1 do (8) $T{_{\left( {0,j} \right)}^{k'}} = T_{\left( {0,j} \right)}^k({P_{(0,j)} })$ (9) $r_P^k = {\text{average} }(T{_{\left( {0,j} \right)}^{k'}})$ (10) end for (11) end for 模板匹配阶段 (12) for i from 0 by 1 to l –1 do (13) cti = 构造密文(ct, i) (14) tri =Saber KEM.Dec(cti) (15) for j from 0 by 1 to 7 do (16) ${ {\rm{tr} }'_{(i,j)} } = { {\rm{tr} }_i}({P_{(0,j)} })$ (17) for k from 0 by 1 to j+1 do (18) $\varGamma _{(i,j)}^k = { {\rm{SOSD} } } ({ {\rm{tr} }'_{(i,j)} },r_P^k)$ (19) end for (20) ${{\rm{HW}}} (m[i,j]) = \min (\varGamma _{(i,j)}^k)$ (21) $m{[i]_j} = {\text{Recover} }({{\rm{HW}}} (m[i,j]),{{\rm{HW}}} (m[i,j] - 1))$ (22) end for (23) end for 表 1 不同方案实验结果
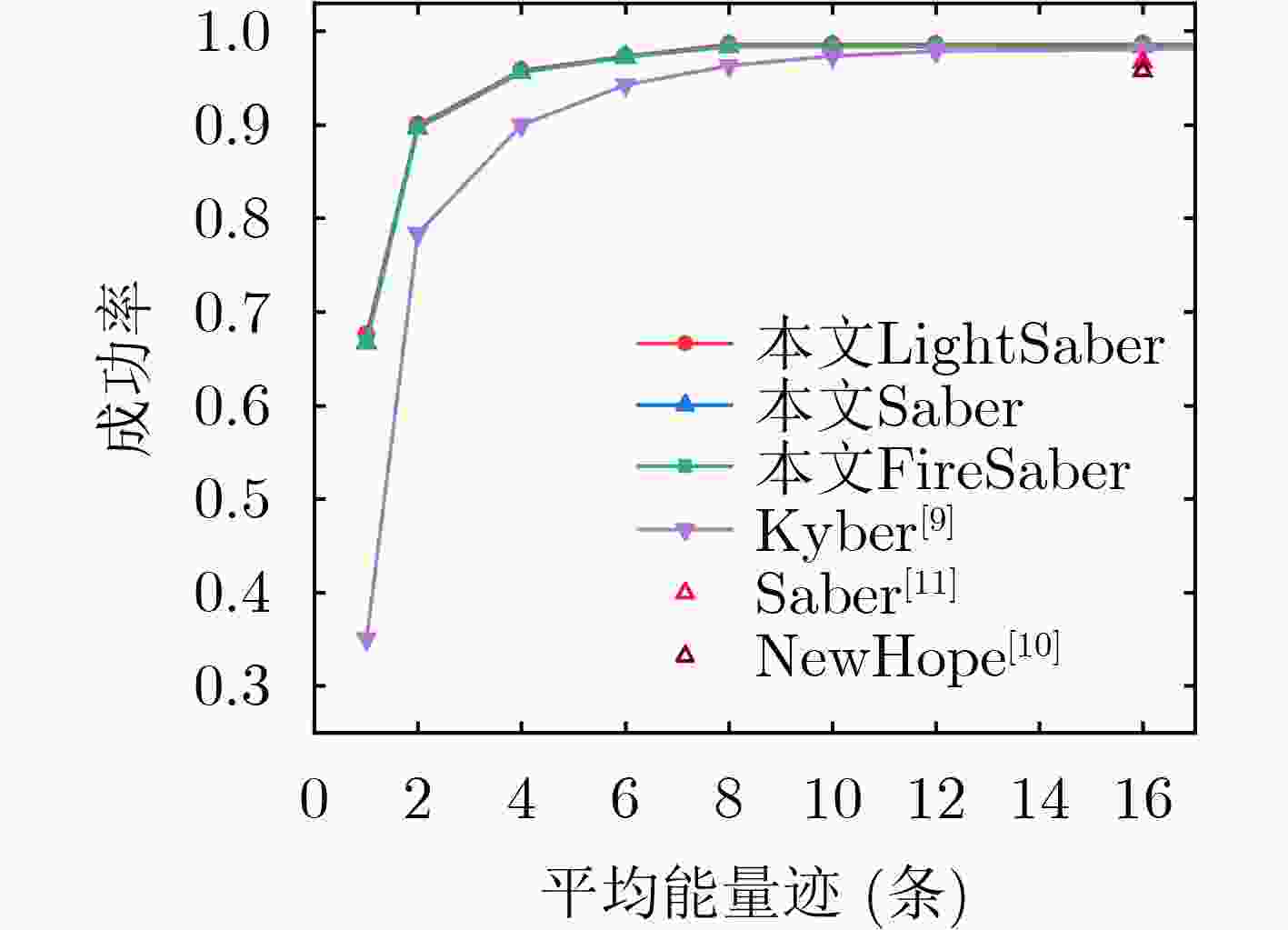
表 2 不同SNR条件下恢复秘密消息的成功率
实验 重复测量次数 成功率*(%) 实验1 1 67.50/66.71/66.68 实验2 2 90.00/89.67/89.63 实验3 4 95.81/95.64/95.64 实验4 6 97.36/97.22/97.20 实验5 8 98.62/98.43/98.37 实验6 10 98.62/98.43/98.39 实验7 12 98.62/98.43/98.39 *:成功率分别为LightSaber/Saber/FireSaber -
[1] 李子臣, 谢婷, 张卷美. 基于RLWE问题的后量子口令认证密钥交换协议[J]. 电子学报, 2021, 49(2): 260–267. doi: 10.12263/DZXB.20190101LI Zichen, XIE Ting, and ZHANG Juanmei. Post Quantum password-based authentication key exchange protocol based on ring learning with errors problem[J]. Acta Electronica Sinica, 2021, 49(2): 260–267. doi: 10.12263/DZXB.20190101 [2] KOCHER P, JAFFE J, and JUN B. Differential power analysis[C]. 19th Advances in Cryptology-CRYPTO’ 99, Berlin, Germany: Springer, 1999. 388–397. [3] 陈华, 习伟, 范丽敏, 等. 密码产品的侧信道分析与评估[J]. 电子与信息学报, 2020, 42(8): 1836–1845. doi: 10.11999/JEIT190853CHEN Hua, XI Wei, FAN Limin, et al. Side channel analysis and evaluation on cryptographic products[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1836–1845. doi: 10.11999/JEIT190853 [4] PRIMAS R, PESSL P, and MANGARD S. Single-trace side-channel attacks on masked lattice-based encryption[C]. 19th Cryptographic Hardware and Embedded Systems – CHES 2017, Cham, Switzerland, 2017: 513–533. [5] PESSL P and PRIMAS R. More practical single-trace attacks on the number theoretic transform[C]. 6th Progress in Cryptology – LATINCRYPT 2019, Cham, Switzerland, 2019: 130–149. [6] RAVI P, ROY S S, CHATTOPADHYAY A, et al. Generic Side-channel Attacks on CCA-secure lattice-based PKE and KEMs[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020, 2020(3): 307–335. doi: 10.13154/tches.v2020.i3.307-335 [7] AYDIN F, AYSU A, TIWARI M, et al. Horizontal side-channel vulnerabilities of post-quantum key exchange and encapsulation protocols[J]. ACM Transactions on Embedded Computing Systems, 2021, 20(6): 110. doi: 10.1145/3476799 [8] XU Zhuang, PEMBERTON O, ROY S S, et al. Magnifying side-channel leakage of lattice-based cryptosystems with chosen ciphertexts: the case study of kyber[J]. IEEE Transactions on Computers, 2022, 71(9): 2163–2176. doi: 10.1109/TC.2021.3122997 [9] RAVI P, BHASIN S, ROY S S, et al. Drop by Drop you break the rock - Exploiting generic vulnerabilities in Lattice-based PKE/KEMs using EM-based Physical Attacks[EB/OL]. IACR Cryptology ePrint Arch, 2020: 549. [10] AMIET D, CURIGER A, LEUENBERGER L, et al. Defeating NewHope with a single trace[C]. 11th Post-Quantum Cryptography - PQCrypto 2020, Cham, Switzerland, 2020: 189–205. [11] SIM B Y, KWON J, LEE J, et al. Single-trace attacks on message encoding in lattice-based KEMs[J]. IEEE Access, 2020, 8: 183175–183191. doi: 10.1109/ACCESS.2020.3029521 [12] NGO K, DUBROVA E, GUO Qiao, et al. A side-channel attack on a masked IND-CCA secure saber KEM implementation[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(4): 676–707. doi: 10.46586/tches.v2021.i4.676-707 [13] NGO K, DUBROVA E, and JOHANSSON T. Breaking masked and shuffled CCA secure saber KEM by power analysis[C]. The 5th Workshop on Attacks and Solutions in Hardware Security, Virtual Event, Korea, 2021. 51–61. [14] D’ANVERS J. Saber algorithm specifications and supporting documentation[OL]. https://csrc.nist.gov/projects/postquantum-cryptography/round-3-submissions. 2020. [15] BANERJEE A, PEIKERT C, and ROSEN A. Pseudorandom functions and lattices[C]. 31st Advances in Cryptology – EUROCRYPT 2012, Berlin, Germany, 2012. 719–737. [16] GOODWILL G, JUN B, JAFFE J, et al. A testing methodology for side channel resistance validation[C]. NIST Non-Invasive Attack Testing Workshop, Gaithersburg, USA, 2011: 115–136. [17] WELCH B L. The generalization of ‘STUDENT'S’ problem when several different population varlances are involved[J]. Biometrika, 1947, 34(1/2): 28–35. doi: 10.1093/biomet/34.1-2.28 [18] BHASIN S, DANGER J L, GUILLEY S, et al. NICV: Normalized inter-class variance for detection of side-channel leakage[C]. 2014 International Symposium on Electromagnetic Compatibility, Tokyo, Japan, 2014. 310–313. [19] KANNWISCHER M J, RIJNEVELD J, SCHWABE P, et al. PQM4: Post-quantum crypto library for the ARM Cortex-M4[EB/OL]. https://github.com/mupq/pqm4, 2020. -





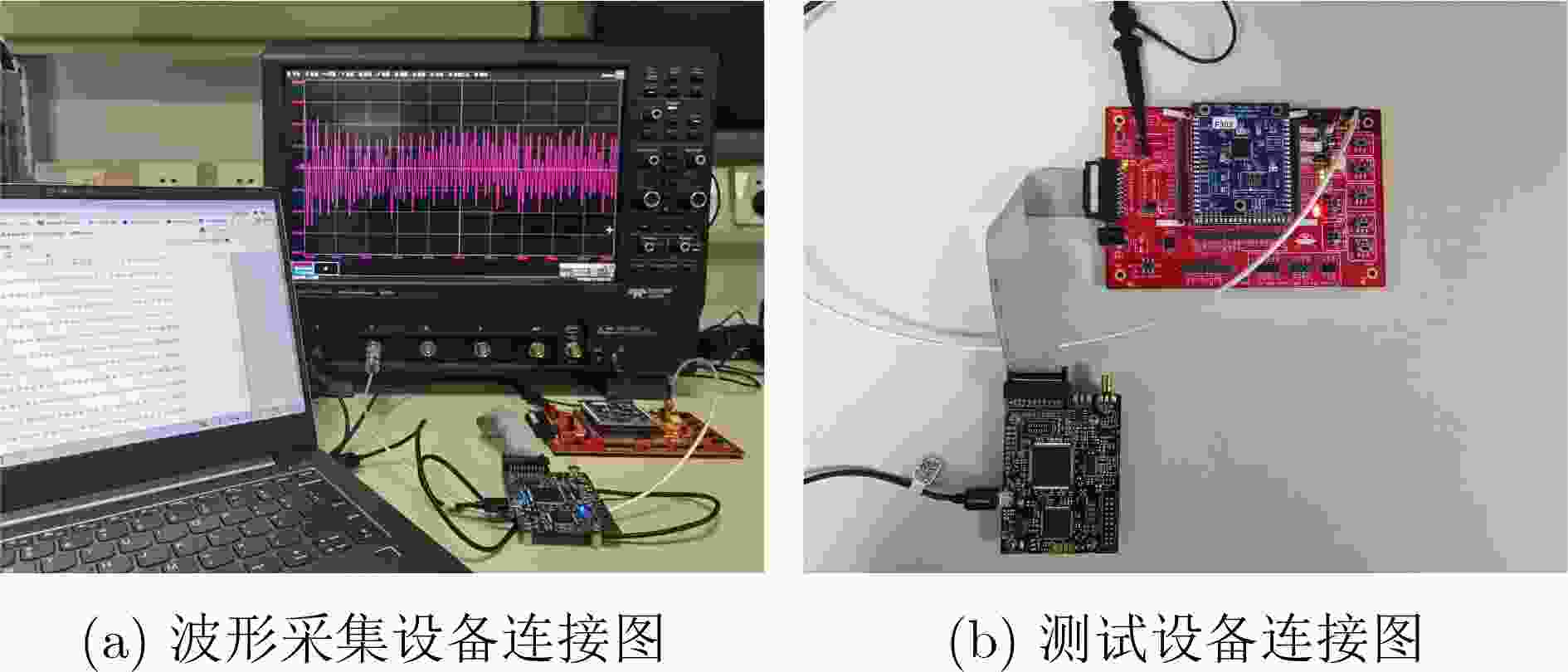
 下载:
下载:

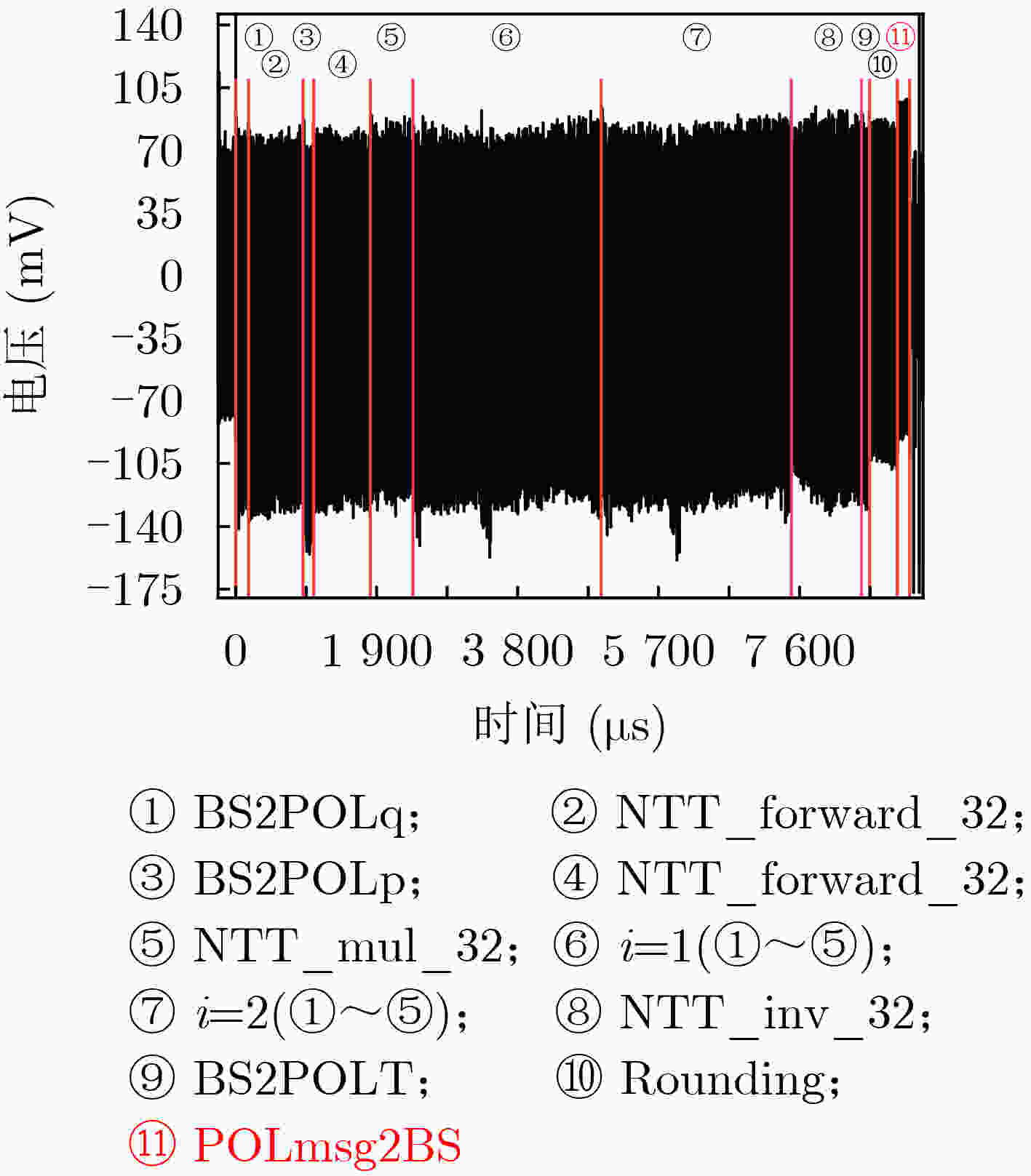
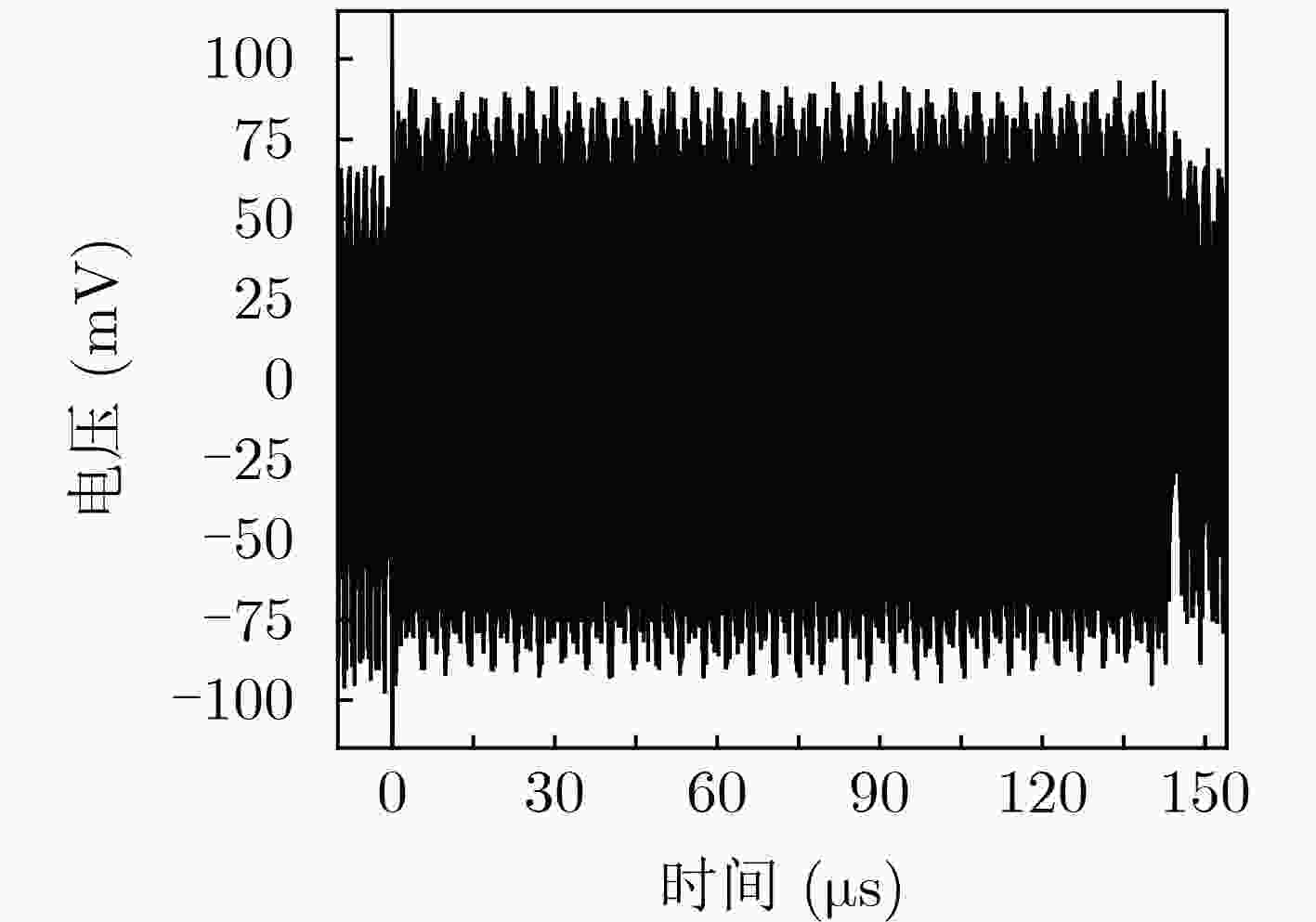


 下载:
下载:
