Multi-User Multi-Carrier Correlated Delay Shift Keying System Based on Time Slot Transformation
-
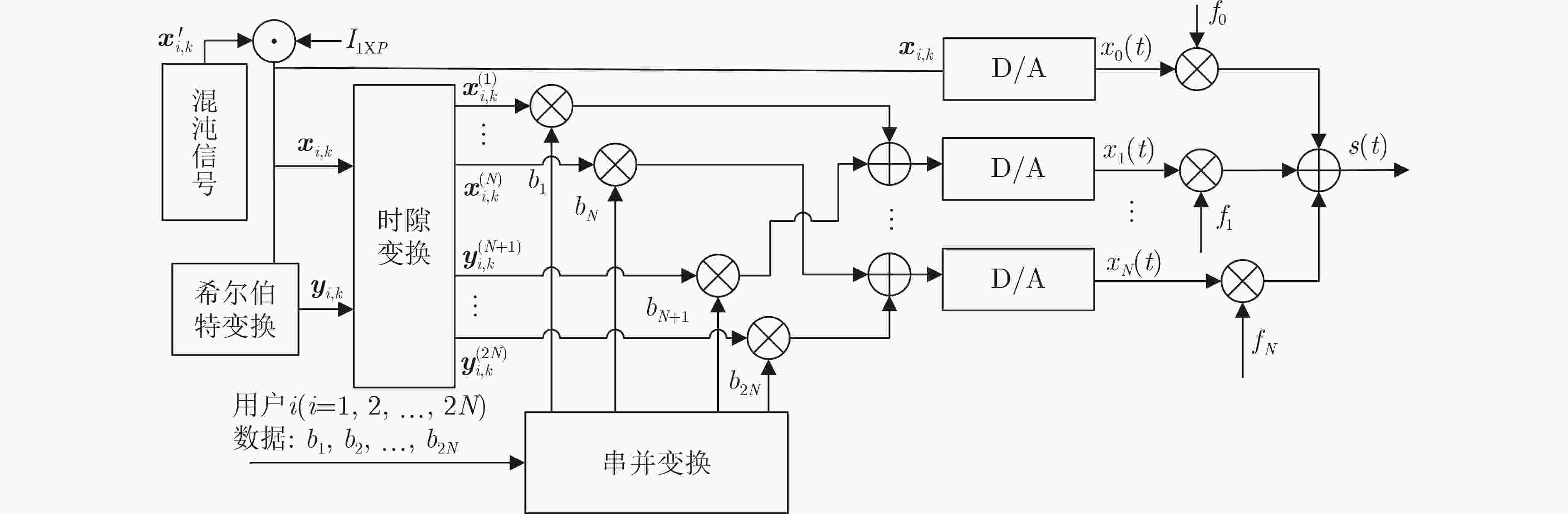
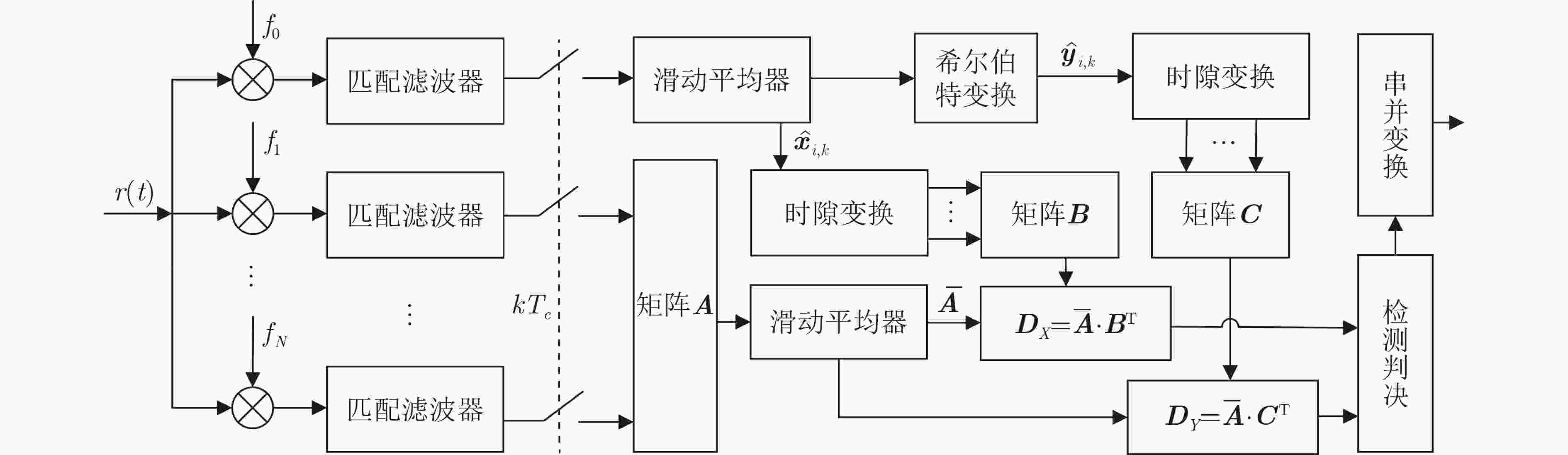
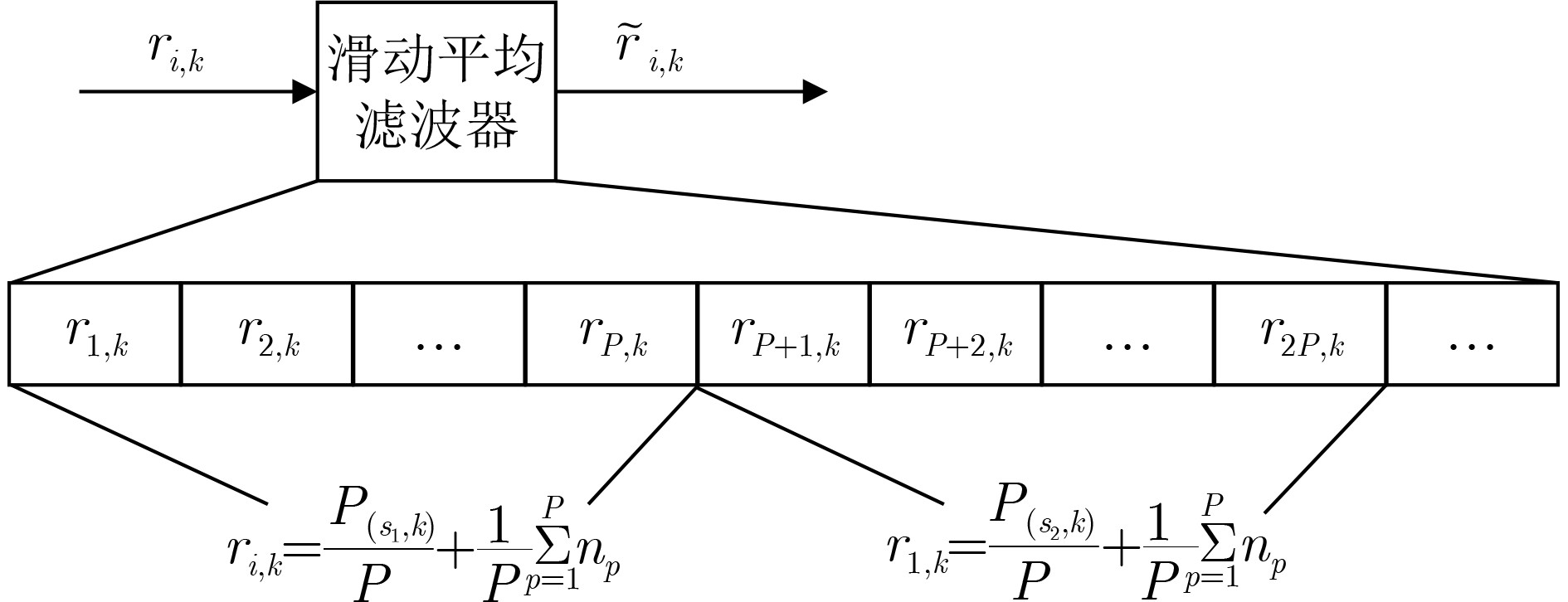
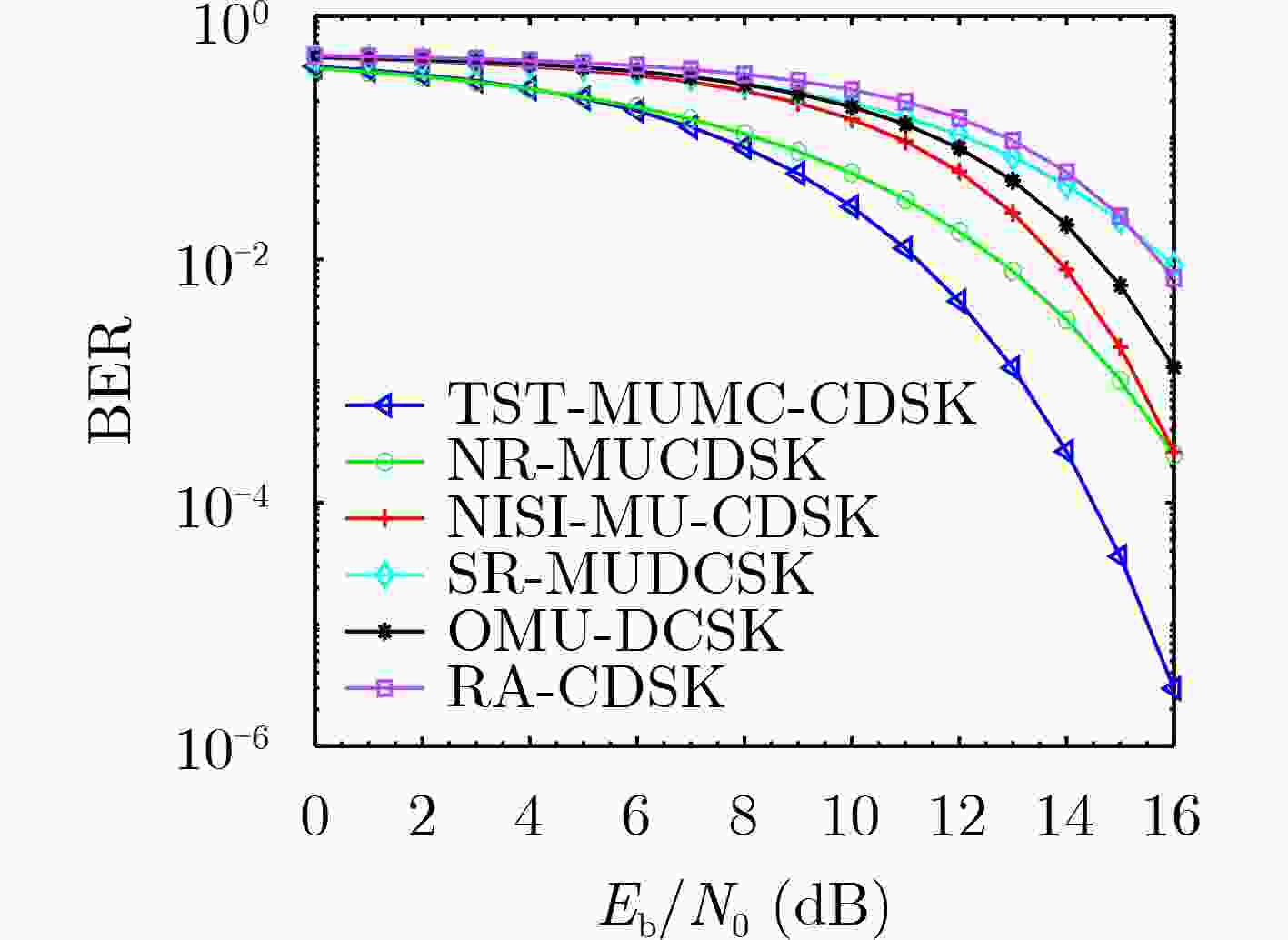
摘要: 为了改善多用户相关延迟移位键控(CDSK)系统误码率(BER)较高的缺点,该文提出一种基于时隙变换的多用户多载波相关延迟移位键控(TST-MUMC-CDSK)系统。该方案采用置换矩阵对参考信号进行变换达到传输多用户信息的目的。在发送端,复制P次之后的混沌信号与经过希尔伯特变换的正交信号一同经过时隙变换器,产生2N个相互正交的混沌信号来承载2N个用户信息,大大提高了系统的传输速率。该文推导了该系统在加性高斯白噪声(AWGN)信道和瑞利衰落信道(RFC)下的误码率表达式,通过理论分析以及数值仿真验证了理论推导的正确性。仿真结果表明对比于其他同类系统,所提系统在相同误码率的情况下可以节约更多的比特能量,在误码率同为10–2时,该系统所需的信噪比比降噪多用户相关延迟移位键控(NR_MUCDSK)系统低1.5 dB,比无信号间干扰多用户相关延迟移位键控(NISI_MU_CDSK)系统低2.6 dB。该系统具有良好的理论价值,且为实际工程应用提供了良好的参考。Abstract: In order to improve the high Bit Error Rate(BER) of multi-user Correlated Delay Shift Keying(CDSK) system, a Multi-User Multi-Carrier Correlated Delay Shift Keying system based on Time Slot Transformation (TST-MUMC-CDSK) system is proposed. The scheme uses a permutation matrix to transform the reference signal for the purpose of transmitting multi-user information. At the transmitter, the chaotic signals are copied P times and passed through the time slot converter together with the Hilbert transformed orthogonal signals, resulting in 2N mutually orthogonal chaotic signals to carry 2N user messages, greatly increasing the transmission rate of the system. In this paper, the theoretical BER expressions of the system are derived for the Additive White Gaussian Noise (AWGN) channel and the Rayleigh Fading Channel (RFC), and the correctness of the theoretical derivation is verified by numerical simulation. Simulation results show that the proposed system can save more bit energy with the same BER than other similar systems, and the required signal-to-noise ratio is 1.5 dB lower than that of Noise Reduction Multi-User Correlated Delay Shift Keying(NR_MUCDSK) and 2.6 dB lower than that of Multi-User Correlated Delay Shift Keying with No Intra-Signal Interference(NISI_MU_CDSK) at the same BER of 10-2. The system has good theoretical value and provides a good reference for practical engineering applications.
-
表 1 TST_MUMC_CDSK与其他系统的传输速率和能量效率对比
系统 传输速率R 能量效率EE TST_MUMC_CDSK $ 2N/\beta {T_c} $ $ 2N/(2N + 1) $ NISI_MU_CDSK $ N/\beta {T_c} $ $ N/(N + 1) $ NR_MUCDSK $ 2N/\beta {T_c} $ $ N/(N + 1) $ CDSK $ 1/\beta {T_c} $ 1/2 -
[1] XU Weikai, HUANG Tingting, and WANG Lin. Code-shifted differential chaos shift keying with code index modulation for high data rate transmission[J]. IEEE Transactions on Communications, 2017, 65(10): 4285–4294. doi: 10.1109/TCOMM.2017.2725261 [2] CHENG Guixian, WANG Lin, XU Weikai, et al. Carrier index differential chaos shift keying modulation[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2017, 64(8): 907–911. doi: 10.1109/TCSII.2016.2613093 [3] CAO Xuepeng, LV Yibo, HUANG Tingting, et al. Performance of different DCSK schemes over the UWB in- body channel[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2016, 28(1): 72–77. [4] KOLUMBÁN G, VIZVÁRI B, SCHWARZ W, et al. Differential chaos shift keying: A robust coding for chaos communication[J]. proc ndes, 1996. https://www.researchgate.net/publication/239666158_Differential_chaos_shift_keying_A_robust_coding_for_chaos_communication. [5] SUSHCHIK M, TSIMRING L S, and VOLKOVSKII A R. Performance analysis of correlation-based communication schemes utilizing chaos[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications, 2000, 47(12): 1684–1691. doi: 10.1109/81.899920 [6] 徐思远, 杨华, 蒋国平. 短参考载波索引差分混沌移位键控通信方案[J]. 南京邮电大学学报:自然科学版, 2021, 41(4): 35–42. doi: 10.14132/j.cnki.1673-5439.2021.04.005XU Siyuan, YANG Hua, and JIANG Guoping. Short reference carrier-index differential chaos shift keying modulation scheme[J]. Journal of Nanjing University of Posts and Telecommunications:Natural Science Edition, 2021, 41(4): 35–42. doi: 10.14132/j.cnki.1673-5439.2021.04.005 [7] KADDOUM G, RICHARDSON F D, GAGNON F, et al. Design and analysis of a multi-carrier differential chaos shift keying communication system[J]. IEEE Transactions on Communications, 2013, 61(8): 3281–3291. doi: 10.1109/TCOMM.2013.071013.130225 [8] KADDOUM G. Design and performance analysis of a multiuser OFDM based differential chaos shift keying communication system[J]. IEEE Transactions on Communications, 2016, 64(1): 249–260. doi: 10.1109/TCOMM.2015.2502259 [9] KADDOUM G and SOUJERI E. NR-DCSK: A noise reduction differential chaos shift keying system[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2016, 63(7): 648–652. doi: 10.1109/TCSII.2016.2532041 [10] TALEB F, BENDIMERAD F T, and ROVIRAS D. Very high efficiency differential chaos shift keying system[J]. IET Communications, 2016, 10(17): 2300–2307. doi: 10.1049/iet-com.2016.0411 [11] QUYEN N X. On the study of a quadrature DCSK modulation scheme for cognitive radio[J]. International Journal of Bifurcation and Chaos, 2017, 27(9): 1750135. doi: 10.1142/S0218127417501358 [12] 张刚, 和华杰, 张天骐. 无信号内干扰的降噪多用户CDSK混沌通信系统[J]. 系统工程与电子技术, 2020, 42(9): 2098–2106. doi: 10.3969/j.issn.1001-506X.2020.09.28ZHANG Gang, HE Huajie, and ZHANG Tianqi. Chaotic communication system of noise reduction multiuser correlation delay shift keying with no intra-signal interference[J]. Systems Engineering and Electronics, 2020, 42(9): 2098–2106. doi: 10.3969/j.issn.1001-506X.2020.09.28 [13] 徐磊, 林文珂, 林文豪, 等. 基于置乱矩阵的短参差分混沌键控系统[J]. 系统工程与电子技术, 2019, 41(10): 2365–2370. doi: 10.3969/j.issn.1001-506X.2019.10.28XU Lei, LIN Wenke, LIN Wenhao, et al. Short-reference differential chaos shift keying system based on scrambling matrix[J]. Systems Engineering and Electronics, 2019, 41(10): 2365–2370. doi: 10.3969/j.issn.1001-506X.2019.10.28 [14] 张刚, 赵畅畅, 张天骐. 基于时间反转的多用户差分混沌键控方案[J]. 上海交通大学学报, 2020, 54(4): 352–358. doi: 10.16183/j.cnki.jsjtu.2020.04.003ZHANG Gang, ZHAO Changchang, and ZHANG Tianqi. Multiuser differential chaos shift keying scheme based on time reverse[J]. Journal of Shanghai Jiaotong University, 2020, 54(4): 352–358. doi: 10.16183/j.cnki.jsjtu.2020.04.003 [15] 张刚, 孟维, 张天骐. 多用户分段移位差分混沌键控通信方案[J]. 电子与信息学报, 2017, 39(5): 1219–1225. doi: 10.11999/JEIT160795ZHANG Gang, MENG Wei, and ZHANG Tianqi. Multiuser communication scheme based on segment shift differential chaos shift keying[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1219–1225. doi: 10.11999/JEIT160795 -





 下载:
下载:
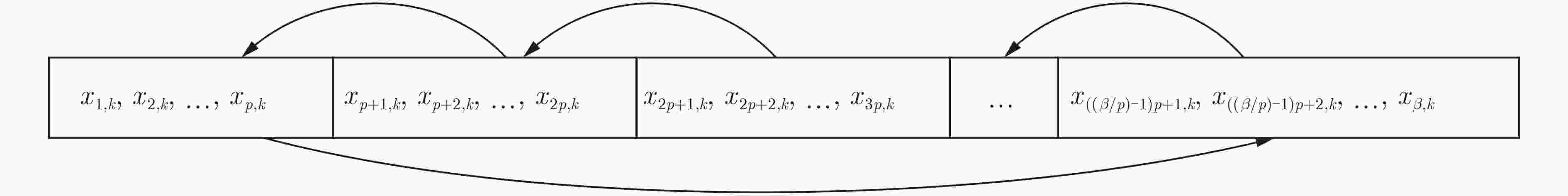


 下载:
下载:
