An Approach of Enhancing the Physical Layer Security of RIS-assisted PD-NOMA Networks Based on Stochastic Geometry
-
摘要: 为提升基于非正交多址访问(NOMA)大规模雾接入网络的上行物理层安全(PLS)，该文考虑了可重构智能表面(RIS)辅助无小区(CF)传输场景。基于功率域复用NOMA(PD-NOMA)并调用随机几何工具将空间效应引入所考虑网络的RIS模型设计，基于该方法来增强其PLS。该网络采用发射机-发射机对建模、Fisher-Snedecor $\mathcal{F}$模型表征复合信道，并重新设计了RIS反射模型。首先推导出所考虑网络组合信道增益的新统计特性，接着推导出RIS辅助PD-NOMA传输场景保密中断概率(SOP)的解析表达式。分析结果和仿真结果表明：该RIS设计能有效提高边缘用户信道质量，从而改变该网络NOMA用户对连续干扰消除(SIC)顺序；该RIS设计及排斥性雾节点(F-AP)部署均可增强该网络PLS，其中，基于β-Ginibre点过程(β-GPP)部署F-AP，在同等条件下，不需增加部署成本即可使SOP至多降低约2个数量级、使保密速率至多提升约$10.5\% $。Abstract: The uplink Physical Layer Security (PLS) of large-scale Non-Orthogonal Multiple Access (NOMA)-based Fog access networks with a Reconfigurable Intelligent Surface (RIS)-assisted Cell-Free (CF) framework is investigated in this paper. The spatial effects of Fog-Access Point (F-AP) locations are introduced into the RIS reflecting model design by invoking stochastic geometry and Power Domain (PD) multiplexing schemes, this spatial-repulsion-based co-design approach is proposed to enhance the PLS of the considered system. This system is modeled with reference to a receiver-transmitter pair, the Fisher-Snedecor $\mathcal{F}$ model is adopted to characterize the composite channel, and the RIS reflecting model is redesigned. The analytical expressions of the Security Outage Probability (SOP) for RIS-assisted PD-NOMA scenarios are derived following the newly expressed channel statistics of the combined channel gains. The analytical and simulation results indicate that the proposed RIS redesign is capable of enhancing the edge users’ channel quality effectively to alter the Successive Interference Cancellation (SIC) orders of NOMA user pairs in this investigated network; The PLS performance of this network can be improved by the proposed RIS redesign and repulsively distributed F-AP deployment, where deploying F-APs in a β-Ginibre Point Process (β-GPP) way can reduce a maximum of two orders of magnitude of the SOP and increase a maximum of $10.5\% $ of the security rate without additional deployment costs under the same conditions.
-
图 2 SOP与用户对总发射功率的关系(${\lambda _{\text{F}}} = {1 \mathord{\left/ {\vphantom {1 {{\text{(}}{{100}^2}\pi {\text{)}}}}} \right. } {{\text{(}}{{100}^2}\pi {\text{)}}}}$)
图 3 SOP与用户对总发射功率的关系(${\lambda _{\text{F}}} = {1 \mathord{\left/ {\vphantom {1 {{\text{(}}{{100}^2}\pi {\text{)}}}}} \right. } {{\text{(}}{{100}^2}\pi {\text{)}}}}$, $N = 16$)
图 4 SOP与用户对总发射功率的关系(${\lambda _{\text{F}}} = {1 \mathord{\left/ {\vphantom {1 {{\text{(}}{{100}^2}\pi {\text{)}}}}} \right. } {{\text{(}}{{100}^2}\pi {\text{)}}}}$, $m = 1$)
-
[1] IMT-2030 (6G)推进组. 6G典型场景和关键能力[R]. 北京: IMT-2030 (6G)推进组, 2022.IMT-2030 (6G) Promotion Group. 6G typical scenarios and key capabilities[R]. Beijing: IMT-2030 (6G) Promotion Group, 2022. [2] WANG Kunlun, ZHOU Yong, LIU Zening, et al. Online task scheduling and resource allocation for intelligent NOMA-based industrial Internet of Things[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(5): 803–815. doi: 10.1109/JSAC.2020.2980908 [3] WEN Xiangming, ZHANG Huiwen, ZHANG Haijun, et al. Interference pricing resource allocation and user-subchannel matching for NOMA hierarchy fog networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 467–479. doi: 10.1109/JSTSP.2019.2899238 [4] WU Qingqing, ZHANG Shuowen, ZHENG Beixiong, et al. Intelligent reflecting surface-aided wireless communications: A tutorial[J]. IEEE Transactions on Communications, 2021, 69(5): 3313–3351. doi: 10.1109/TCOMM.2021.3051897 [5] LI Yun, LIAO Chao, WANG Yong, et al. Energy-efficient optimal relay selection in cooperative cellular networks based on double auction[J]. IEEE Transactions on Wireless Communications, 2015, 14(8): 4093–4104. doi: 10.1109/TWC.2015.2416715 [6] PANG Weina, WANG Ping, HAN Maojie, et al. Optical intelligent reflecting surface for mixed Dual-Hop FSO and beamforming-based RF system in C-RAN[J]. IEEE Transactions on Wireless Communications, 2022, 21(10): 8489–8506. doi: 10.1109/TWC.2022.3166756 [7] SHAWAQFEH M K and BADARNEH O S. Performance of mobile networks under composite $ \mathcal{F}$ fading channels[J]. Digital Communications and Networks, 2022, 8(1): 25–32. doi: 10.1016/j.dcan.2021.01.001 [8] HOU Tianwei, LIU Yuanwei, SONG Zhengyu, et al. Reconfigurable intelligent surface aided NOMA networks[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(11): 2575–2588. doi: 10.1109/JSAC.2020.3007039 [9] YU Xianhua, LI Dong, XU Yongjun, et al. Convolutional autoencoder-based phase shift feedback compression for intelligent reflecting surface-assisted wireless systems[J]. IEEE Communications Letters, 2022, 26(1): 89–93. doi: 10.1109/LCOMM.2021.3123941 [10] DU Hongyang, ZHANG Jiayi, PEPPAS K P, et al. On the distribution of the ratio of products of Fisher-Snedecor $ \mathcal{F} $ random variables and its applications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1855–1866. doi: 10.1109/TVT.2019.2961427 [11] ZWILLINGER D and JEFFREY A. Table of Integrals, Series, and Products[M]. 7th ed. Burlington: Academic Press, 2007. [12] BASAR E. Reconfigurable intelligent surfaces for Doppler effect and multipath fading mitigation[J]. Frontiers in Communications and Networks, 2021, 2: 672857. doi: 10.3389/frcmn.2021.672857 [13] BLOCH M, BARROS J Ã, RODRIGUES M R D, et al. Wireless information-theoretic security[J]. IEEE Transactions on Information Theory, 2008, 54(6): 2515–2534. doi: 10.1109/TIT.2008.921908 [14] YAKUBOVICH S B and NGUYEN T H. The Double Mellin-Barnes Type Integrals and Their Applications To Convolution Theory[M]. Singapore: World Scientific, 1992. [15] MATHAI A M, SAXENA R K, and HAUBOLD H J. The H-Function: Theory and Applications[M]. New York: Springer, 2009. [16] KILBAS A A. H-transforms: Theory and Applications[M]. Boca Raton: CRC Press, 2004. [17] LI Dong. How many reflecting elements are needed for energy- and spectral-efficient intelligent reflecting surface-assisted communication[J]. IEEE Transactions on Communications, 2022, 70(2): 1320–1331. doi: 10.1109/TCOMM.2021.3128544 [18] LI Dong. Bound analysis of number configuration for reflecting elements in IRS-Assisted D2D communications[J]. IEEE Wireless Communications Letters, 2022, 11(10): 2220–2224. doi: 10.1109/LWC.2022.3197614 [19] MOHJAZI L, BARIAH L, MUHAIDAT S, et al. Performance of reconfigurable intelligent surfaces in the presence of generalized Gaussian noise[J]. IEEE Communications Letters, 2022, 26(4): 773–777. doi: 10.1109/LCOMM.2022.3145291 [20] FENG Youhong, YAN Shihao, YANG Nan, et al. Safeguarding non-orthogonal multiple access with physical layer techniques[J]. IEEE Network, 2022, 36(3): 145–151. doi: 10.1109/MNET.014.2100091 [21] XU Yongjun, GUI Guan, OHTSUKI T, et al. Robust resource allocation for two-tier HetNets: An interference-efficiency perspective[J]. IEEE Transactions on Green Communications and Networking, 2021, 5(3): 1514–1528. doi: 10.1109/TGCN.2021.3090592 -
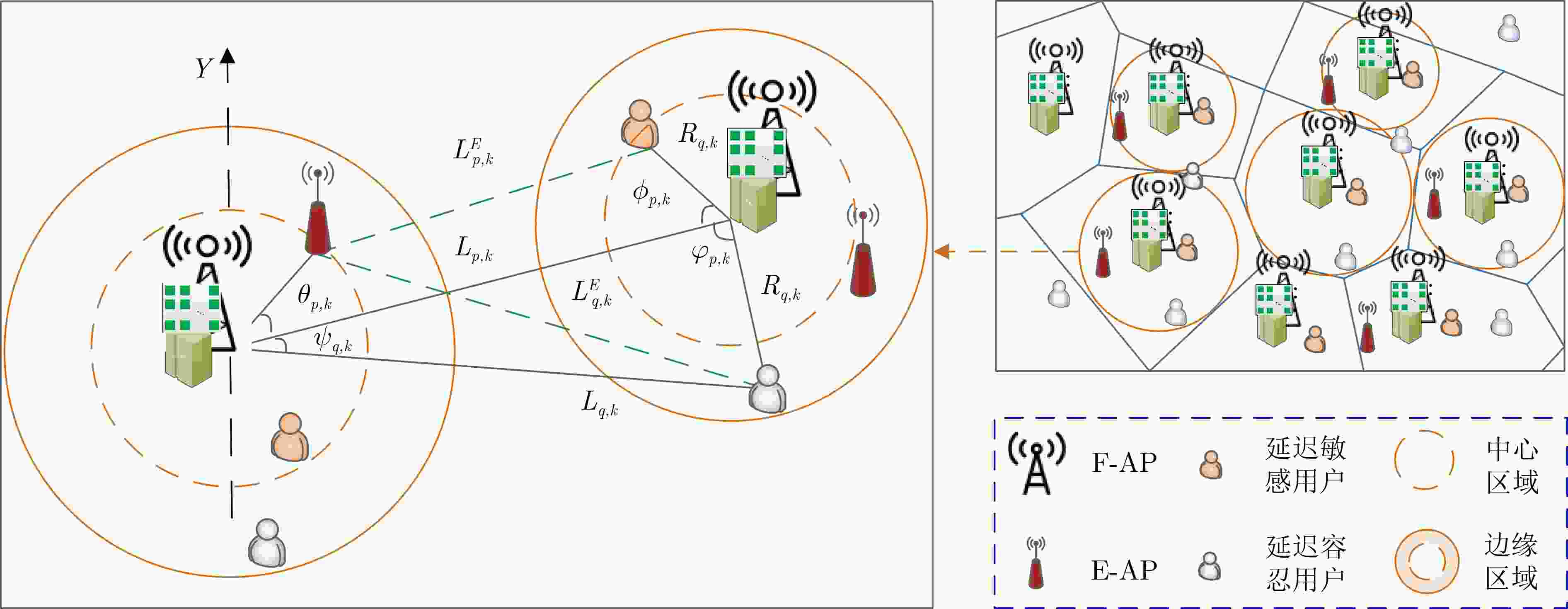
下载:
图(9)
计量
- 文章访问数: 742
- HTML全文浏览量: 353
- PDF下载量: 88
- 被引次数: 0
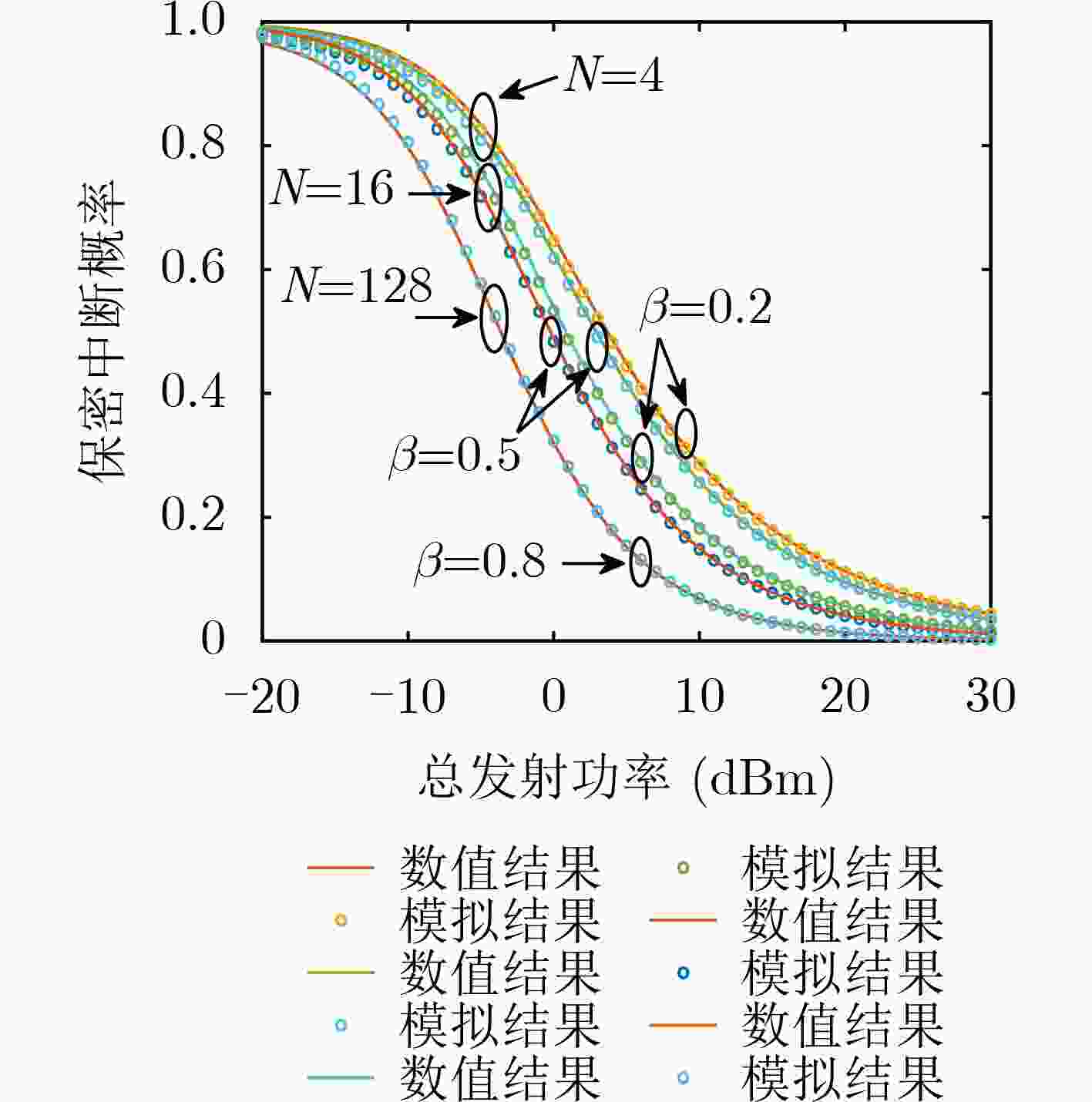
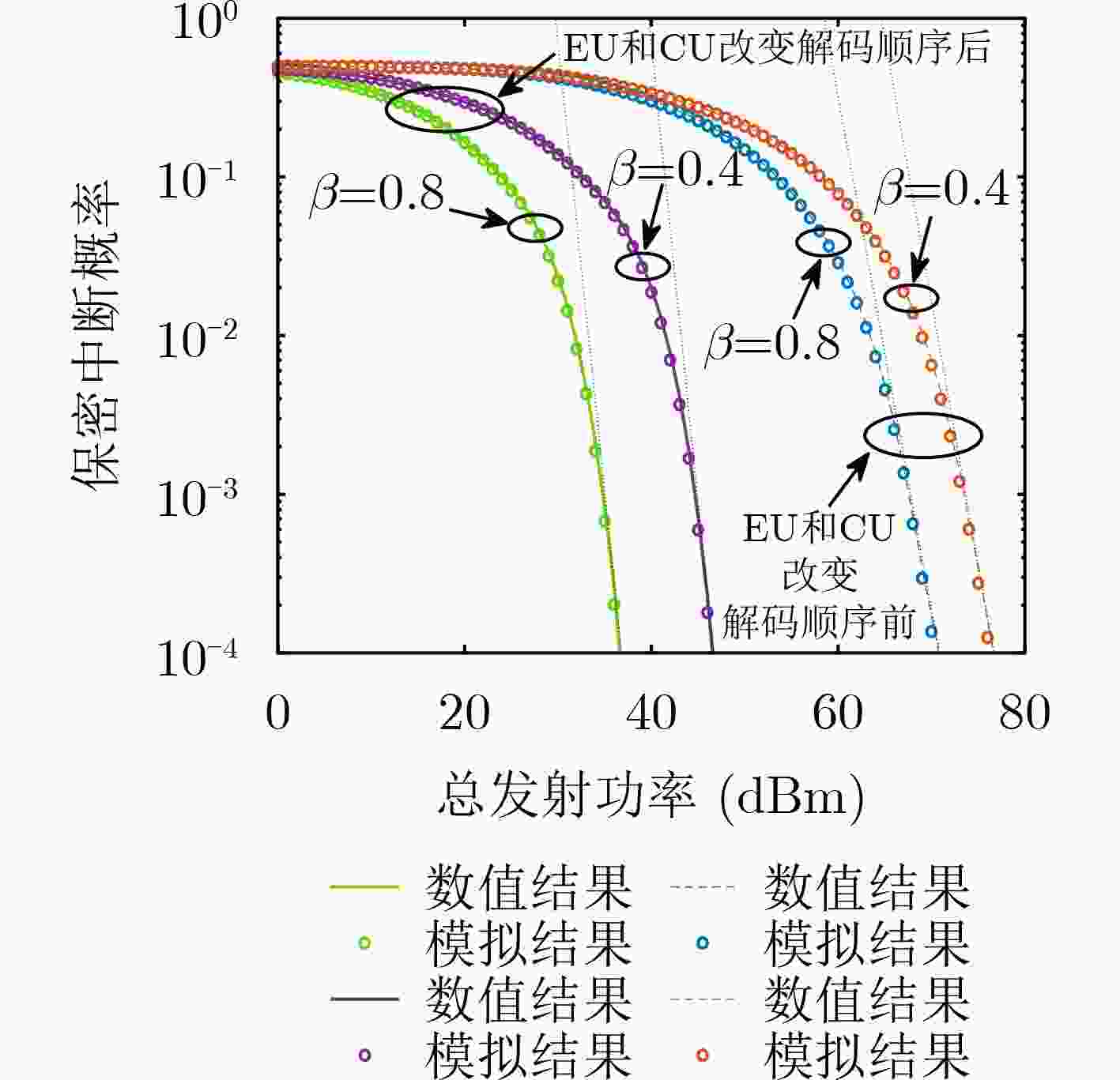
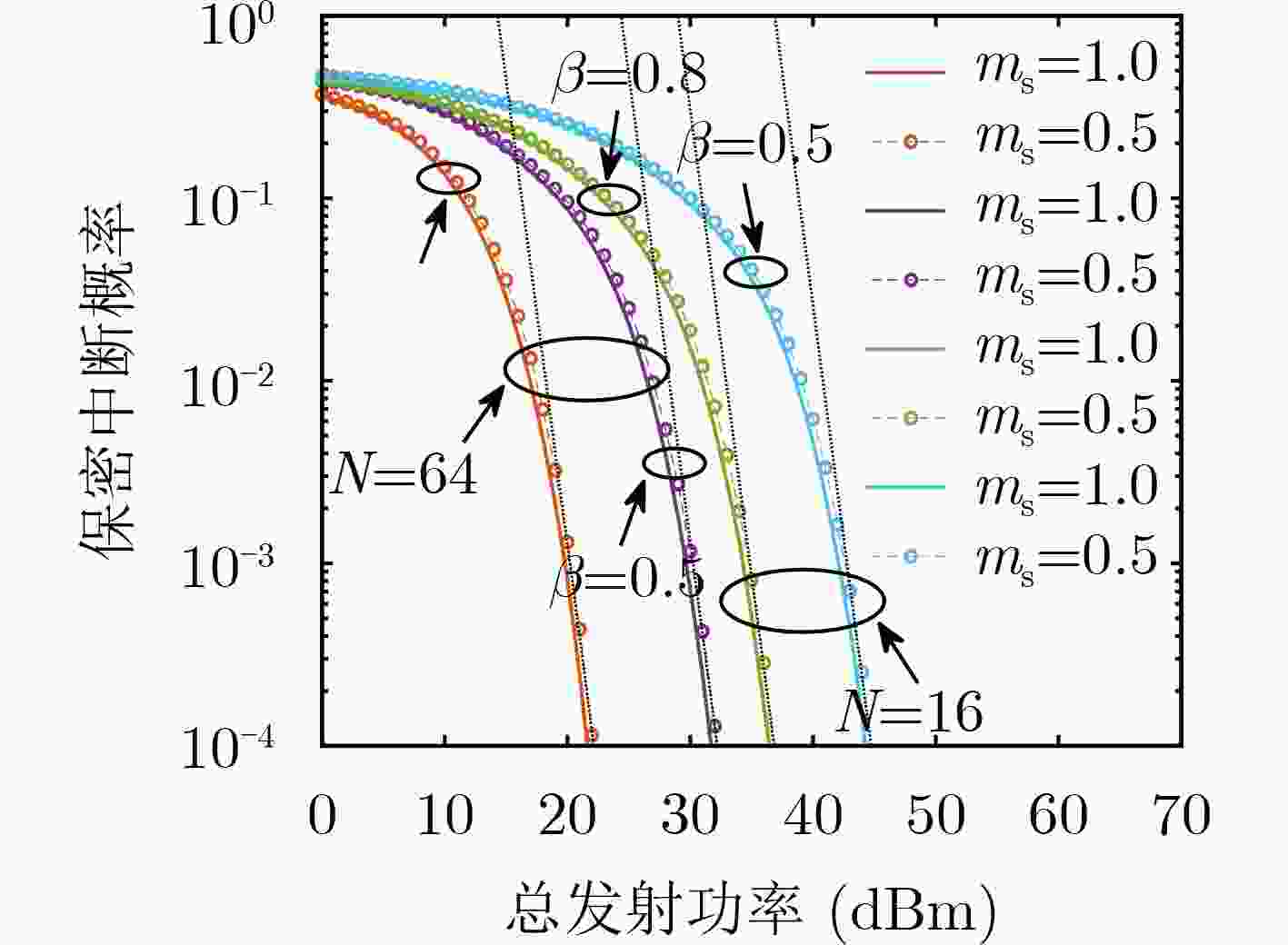
下载:
