基于自适应分块和联合优化光滑<i>l</i><sub>0</sub>范数的二维压缩感知算法

张小贝; 唐辰; 涂喜梅; 陆晓刚; 张琦

doi:10.11999/JEIT221097

基于自适应分块和联合优化光滑l₀范数的二维压缩感知算法

doi: 10.11999/JEIT221097

1.
上海大学通信与信息工程学院上海 200444
2.
上海飞机设计研究院上海 201210

基金项目: 工信部民用飞机专项科研项目(MJZ-2018-S-30)

详细信息

作者简介:
张小贝：男，教授，研究方向为光电信息技术

唐辰：男，硕士生，研究方向为航空图像压缩加密

涂喜梅：女，研究员，研究方向为航空无线通信系统

陆晓刚：男，高级工程师，研究方向为航空数据链通信系统

张琦：男，讲师，研究方向为光电信息技术

通讯作者:
张小贝　xbzhang@shu.edu.com

中图分类号: TN911.73
计量
- 文章访问数: 414
- HTML全文浏览量: 257
- PDF下载量: 115
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-22
- 修回日期: 2023-03-31
- 网络出版日期: 2023-04-04
- 刊出日期: 2023-12-26

2D Compressed Sensing Algorithm Based on Adaptive Blocking and Joint Optimization Smooth l₀ Norm

1.
School of Communication and Information Engineering, Shanghai University, Shanghai 200444, China
2.
Shanghai Aircraft Design and Research Institute, Shanghai 201210, China

Funds: The Ministry of Industry and Information Technology Civil Aircraft Special Research Project (MJZ-2018-S-30)

摘要

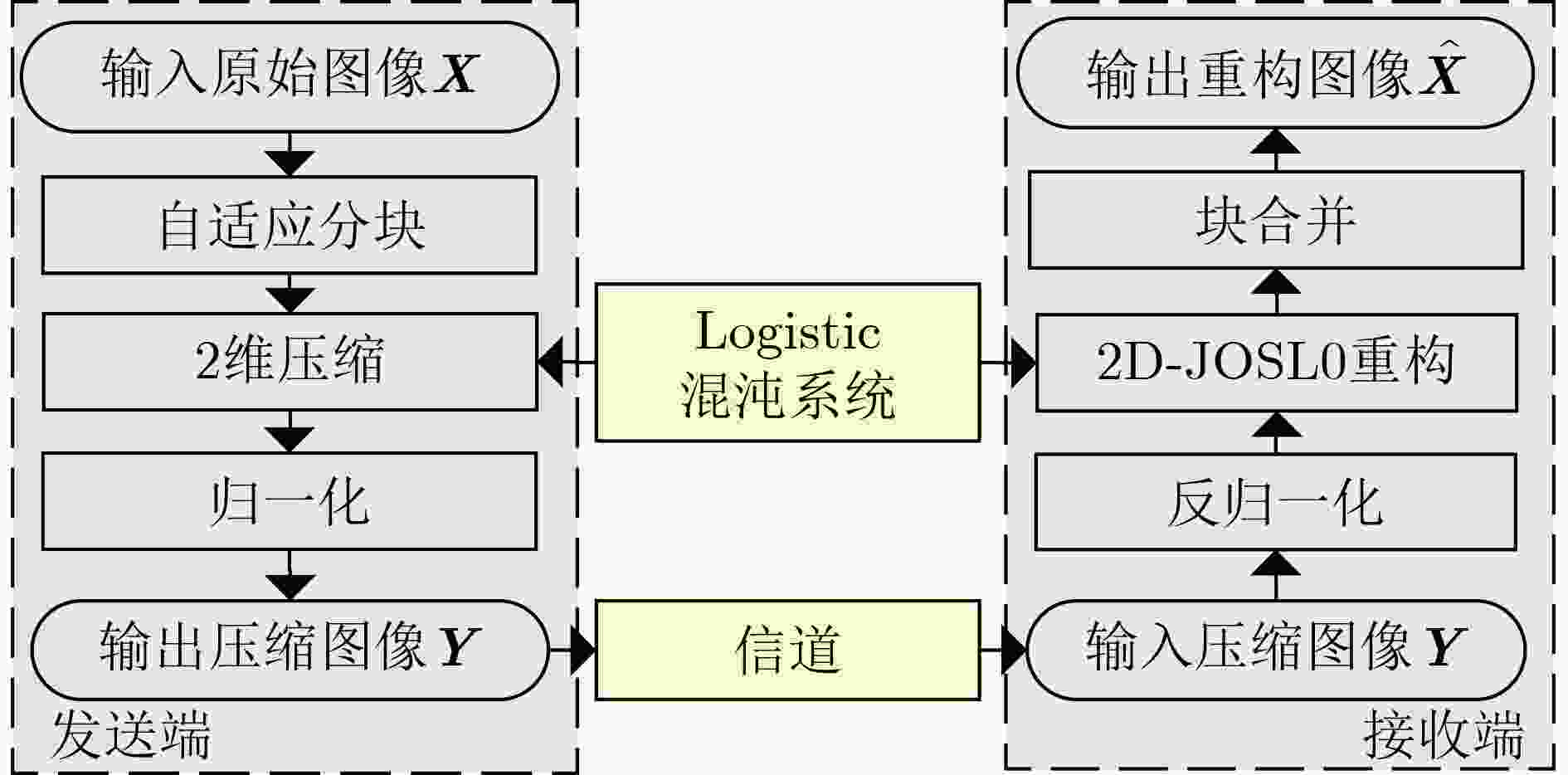
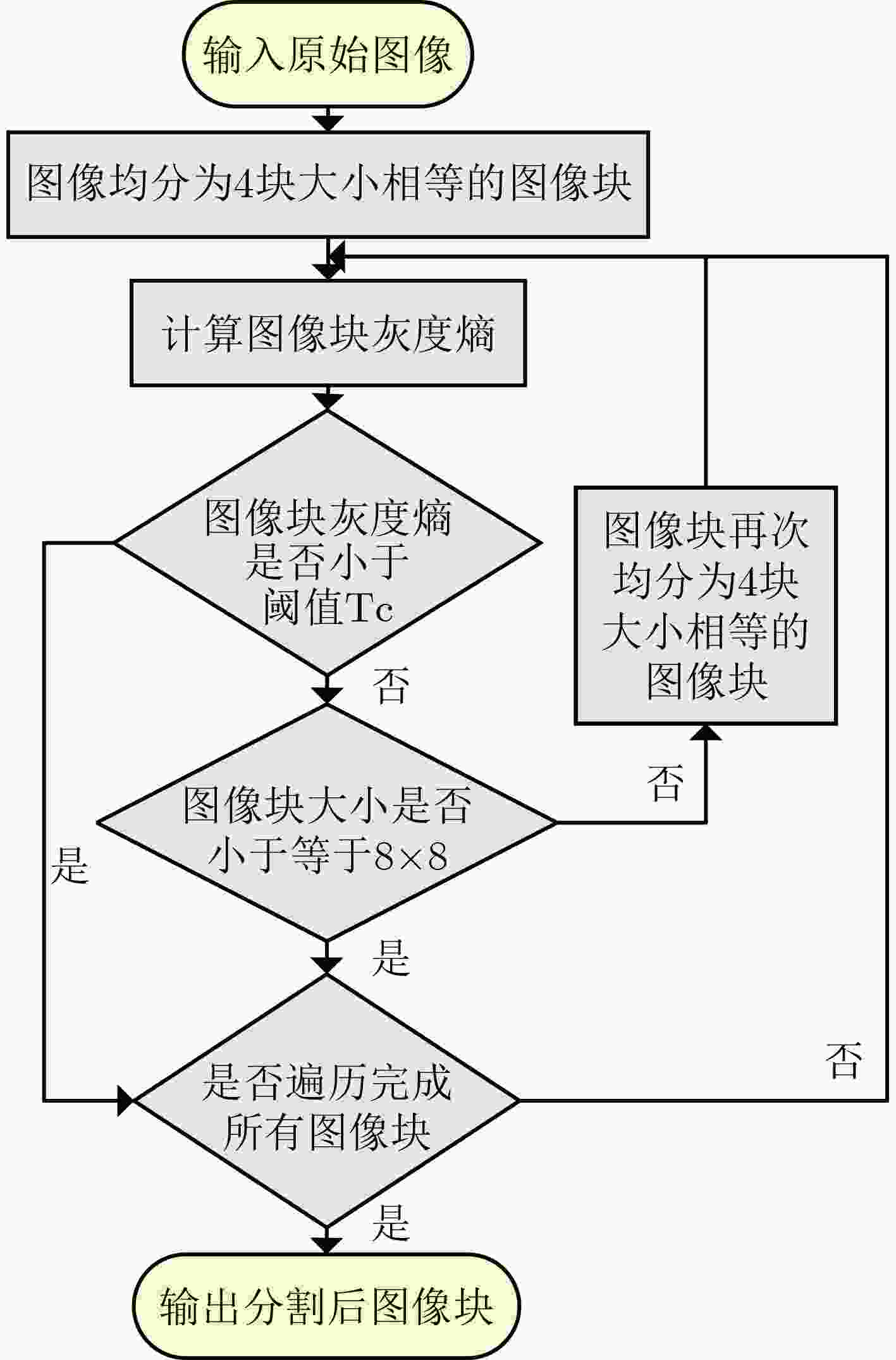
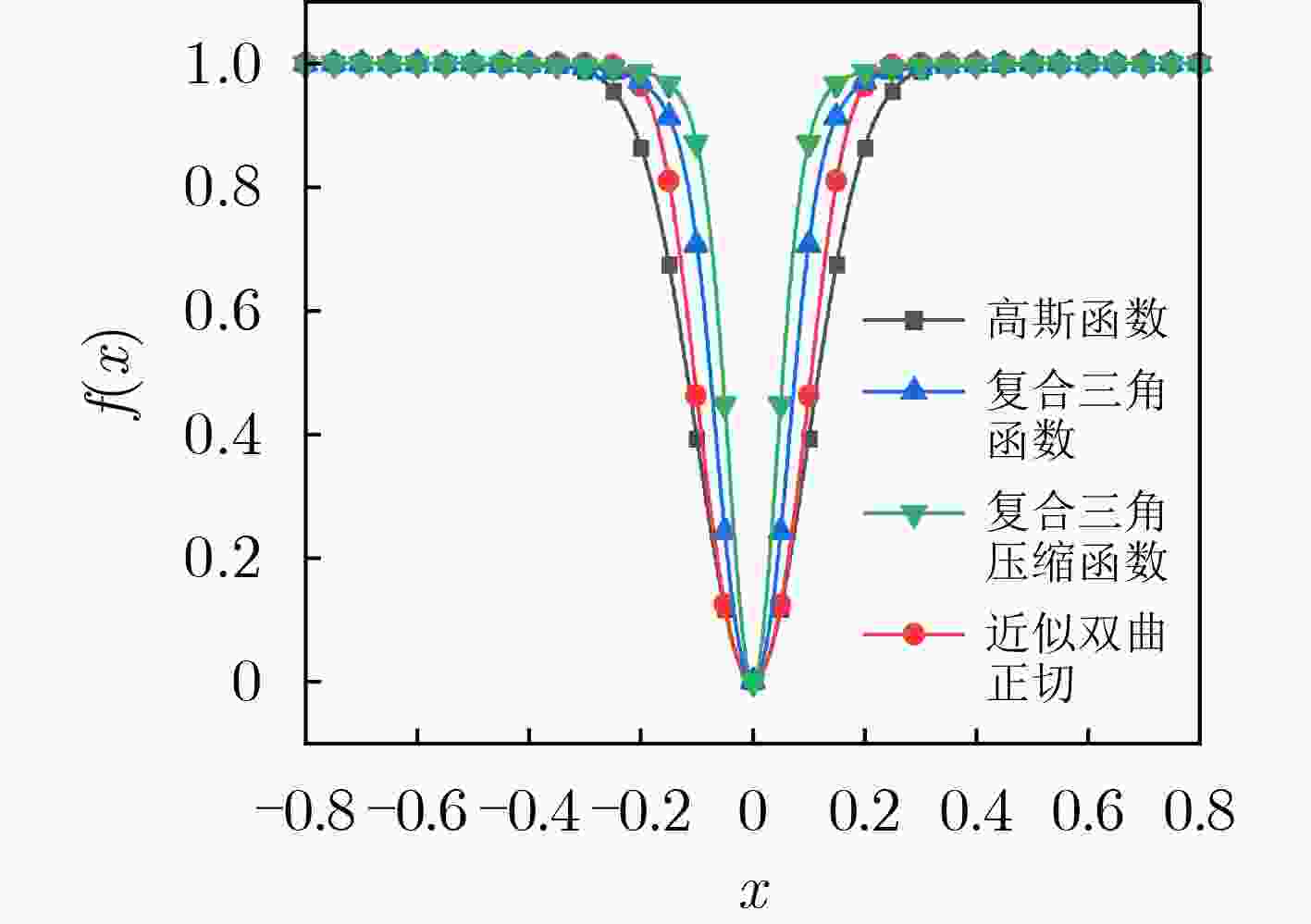
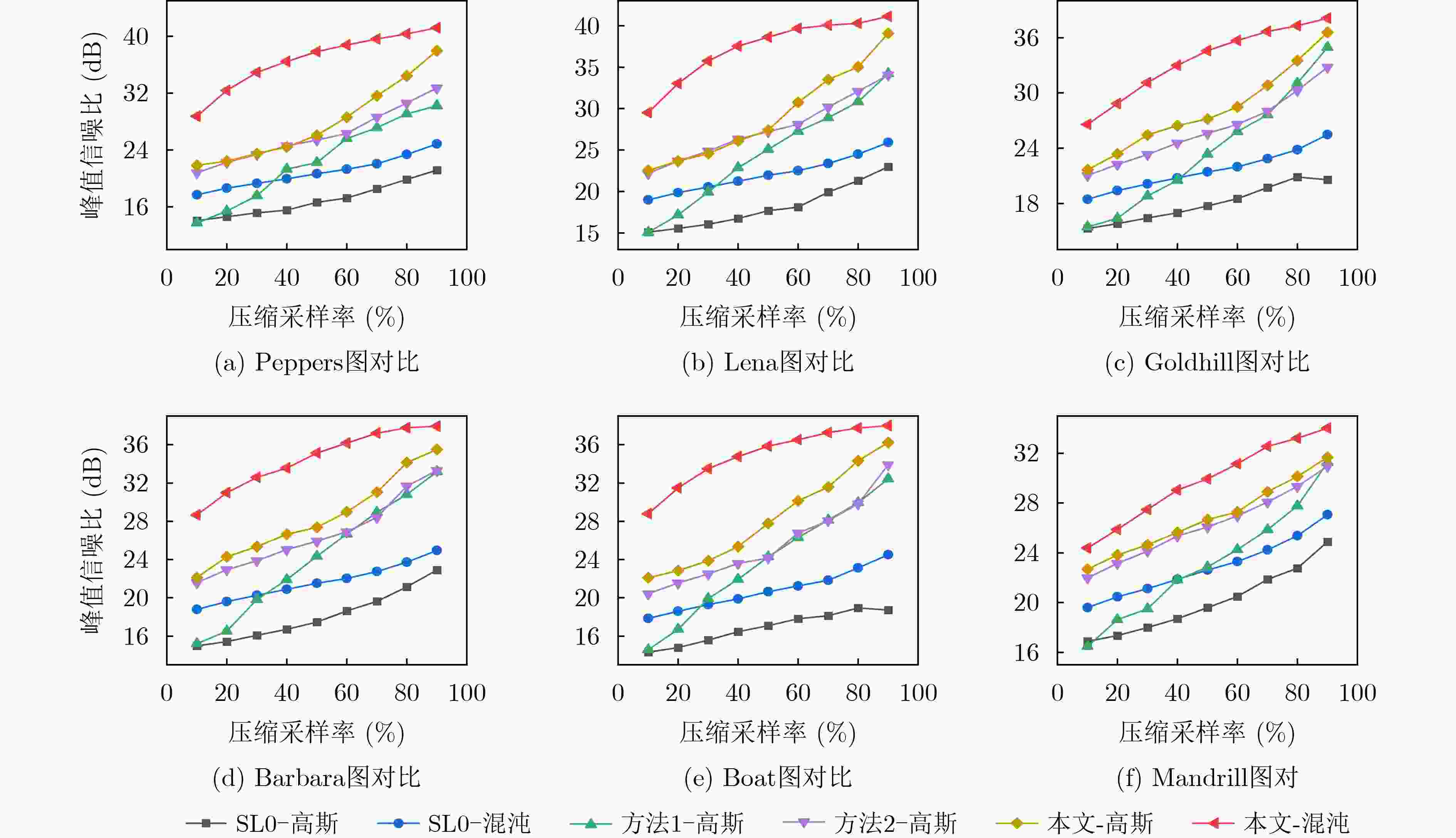
摘要: 传统的压缩感知模型和重构方法，虽能有效减少数据量，但压缩和重构性能不佳，故该文提出一种基于自适应分块和联合优化光滑l₀范数(SL0)的2维压缩感知算法。压缩过程利用灰度熵和四叉树算法进行自适应分块和采样率分配，同时对压缩模型改进，使用混沌循环矩阵作为测量矩阵，提升了压缩性能。重构过程基于SL0算法，采用陡峭性更高的拟合函数，结合拟牛顿法和动态迭代的方案提高重构质量和效率。该算法峰值信噪比和结构相似性指数相比现有算法平均提升了5.44 dB和21.08%，平均计算时间仅需1.59 s，表明该算法能稳定、快速地实现图像的压缩感知和精确重构，为压缩感知和图像重构提供了新方法。
- 2维压缩感知 /
- 自适应分块 /
- 图像重构 /
- 光滑l₀范数算法 /
- 拟牛顿法
Abstract: A 2-dimension compressed sensing algorithm based on adaptive blocking and joint optimization Smooth l₀ (SL0) norm is proposed to solve the problem of poor compression and reconstruction performance of the traditional compressed sensing model and reconstruction method. In the compression process, gray entropy and quadtree algorithm are used for adaptive blocking and sample rate allocation. At the same time, the compressed sensing model is optimized and the chaotic cyclic matrix is used as the measure matrix, which improves the compression performance. In the reconstruction process based on SL0 algorithm, a fitting function with higher steepness and a scheme combined with Quasi-Newton method and dynamic iteration are adopted to improve the reconstruction quality and efficiency. Compared with other algorithms, the peak signal to noise ratio and structural similarity index of the proposed algorithm are improved by 5.44 dB and 21.08% on average respectively. The average calculation time is only 1.59 s. Based on realizing image compression and accurate reconstruction stably and quickly, the proposed algorithm provides a new method for compressed sensing and image reconstruction.
- 2-Dimensional compressed sensing /
- Adaptive blocking /
- Image reconstruction /
- Smooth l₀ algorithm /
- Quasi-Newton method

HTML全文

图 1 2D-ABCS-JOSL0算法流程图

下载: 全尺寸图片幻灯片

图 2 图像自适应分块流程

下载: 全尺寸图片幻灯片

图 3 l₀近似函数对比图

下载: 全尺寸图片幻灯片

图 4 6幅测试图像

下载: 全尺寸图片幻灯片

图 5 图像自适应分块后结果

下载: 全尺寸图片幻灯片

图 6 图像单一优化算法PSNR对比

下载: 全尺寸图片幻灯片

图 7 图像单一优化算法SSIM对比

下载: 全尺寸图片幻灯片

图 8 30%压缩采样率下不同算法Lena图像结果对比

下载: 全尺寸图片幻灯片

图 9 30%压缩采样率下不同算法Barbara图像重构结果对比

下载: 全尺寸图片幻灯片

图 10 不同算法计算时间对比

下载: 全尺寸图片幻灯片

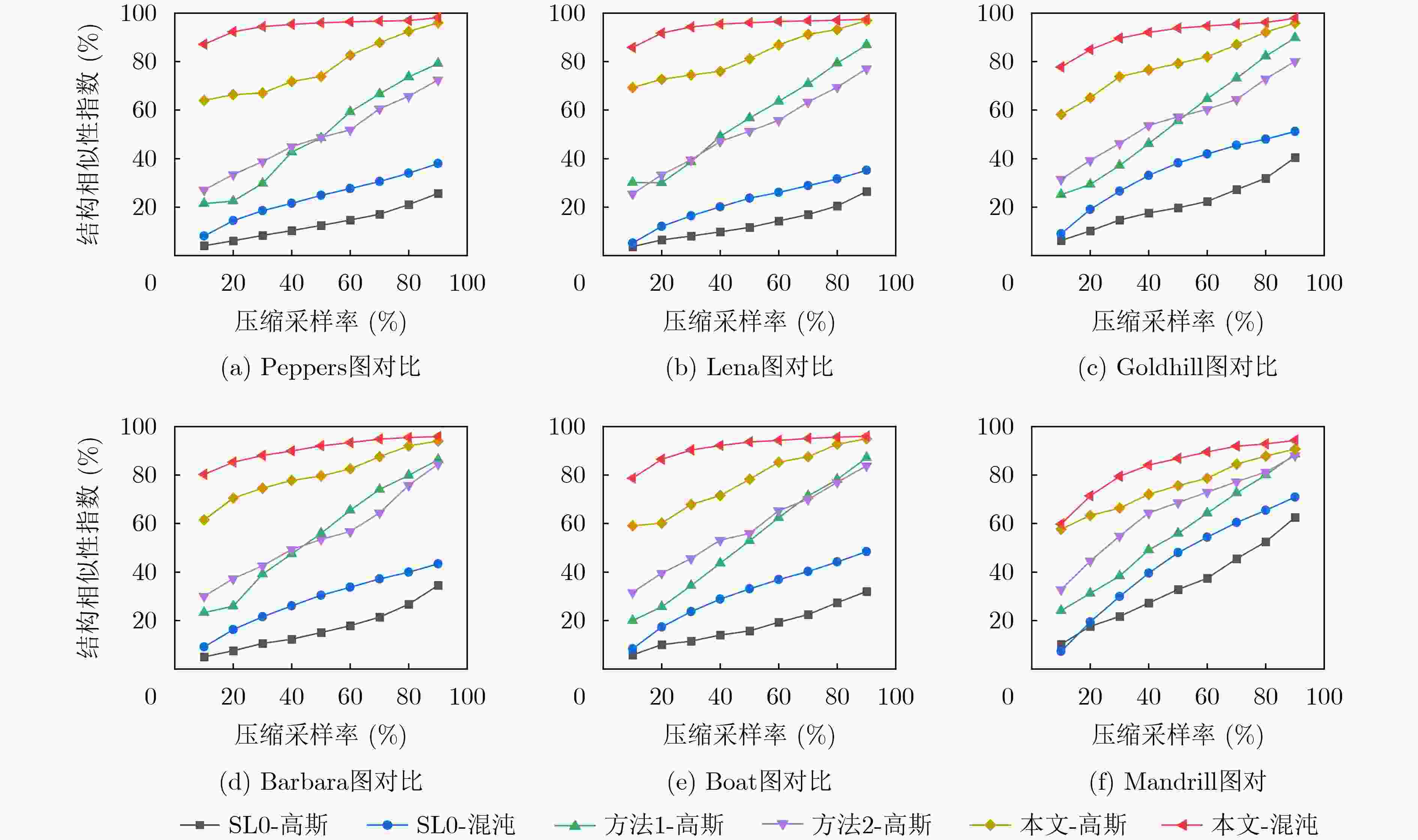
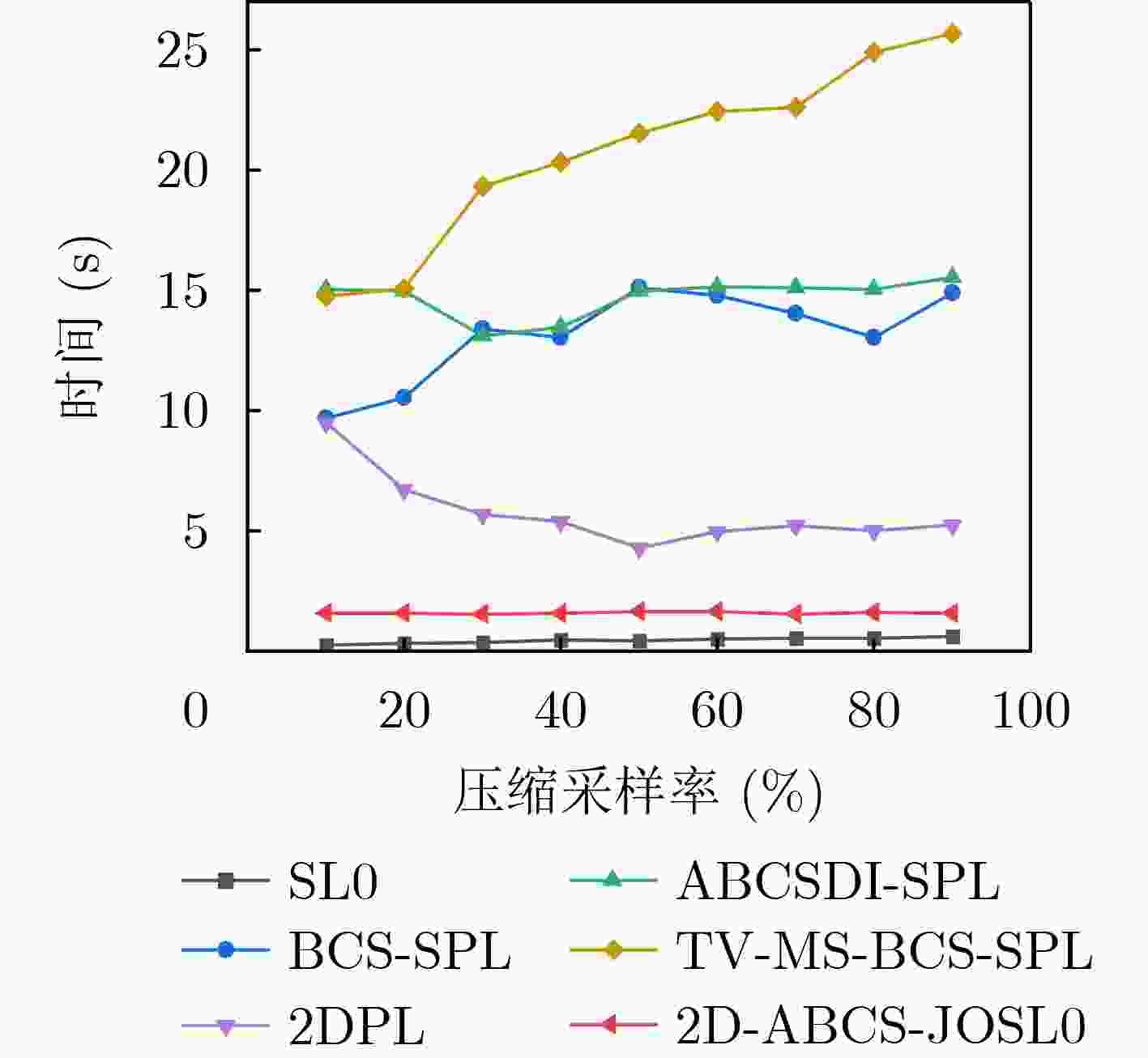
表 1 不同图像不同算法PSNR(dB)/SSIM(%))对比

压缩采样率(%)	算法	Peppers	Lena	Goldhill	Barbara	Boat	Mandrill	平均值
10	BCS-SPL	23.79/64.86	23.58/64.57	26.71/54.98	23.12/55.12	23.64/55.1	22.54/37.15	23.65/55.30
	ABCSDI-SPL	24.79/72.09	24.05/73.87	27.57/57.26	23.97/55.52	24.28/56.54	20.81/36.02	24.24/58.55
	2DPL	27.79/86.81	27.13/83.99	27.05/74.42	24.34/72.96	23.54/73.43	21.89/50.84	25.29/73.74
	TV-MS-BCS-SPL	28.21/87.03	27.33/80.43	28.21/75.89	28.01/74.04	24.27/74.33	22.97/52.32	26.50/74.01
	2D-ABCS-JOSL0	28.75/87.13	29.50/85.89	28.79/78.76	28.67/80.33	26.57/77.84	24.38/59.73	27.77/78.28
30	BCS-SPL	28.54/77.08	29.04/81.35	30.13/73.02	26.20/68.25	26.65/73.42	26.03/52.47	27.35/70.93
	ABCSDI-SPL	29.93/82.50	29.92/87.12	32.09/72.25	30.39/70.01	27.65/73.43	24.54/52.59	29.09/72.98
	2DPL	34.24/94.34	34.33/93.16	30.48/87.91	28.46/85.76	30.48/87.98	26.36/69.88	30.73/86.50
	TV-MS-BCS-SPL	34.32/93.13	30.99/88.94	33.12/83.95	29.76/82.46	28.87/83.32	27.04/73.56	30.68/84.23
	2D-ABCS-JOSL0	34.94/94.49	35.74/94.27	33.51/90.36	32.58/88.11	31.13/89.71	27.47/79.50	32.56/89.41
50	BCS-SPL	31.53/84.90	32.43/87.04	32.85/80.08	30.05/79.54	28.93/82.51	29.38/68.72	30.20/80.47
	ABCSDI-SPL	33.02/88.45	33.72/92.65	33.84/81.54	33.12/81.11	30.02/82.50	26.85/70.32	31.76/82.76
	2DPL	36.75/95.03	37.56/95.29	34.01/91.22	32.64/91.04	34.01/93.72	29.01/86.25	34.00/92.26
	TV-MS-BCS-SPL	36.95/96.00	33.20/92.00	34.84/88.47	33.96/88.91	32.72/90.13	28.04/81.23	33.29/89.46
	2D-ABCS-JOSL0	37.85/96.04	38.61/96.00	35.87/93.67	35.12/92.03	34.58/93.73	29.94/86.95	35.33/93.07
70	BCS-SPL	33.81/90.75	34.87/94.02	34.28/91.19	33.52/87.89	31.89/90.42	32.01/81.02	32.90/89.22
	ABCSDI-SPL	36.71/94.34	38.12/96.14	34.95/89.26	36.01/88.14	33.38/90.99	28.55/82.34	34.62/90.20
	2DPL	38.63/96.55	39.55/96.88	36.98/94.56	36.25/94.65	36.22/95.13	31.83/90.75	36.58/94.75
	TV-MS-BCS-SPL	38.10/96.09	34.92/93.91	36.52/93.87	36.32/93.43	35.93/94.81	31.75/90.12	35.59/93.70
	2D-ABCS-JOSL0	39.64/96.74	40.05/96.88	37.28/95.08	37.21/94.80	36.66/95.54	32.56/91.97	37.23/95.17

下载: 导出CSV

参考文献(24)

[1]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[2]	覃亚丽, 梅济才, 任宏亮, 等. 基于高斯平滑压缩感知分数阶全变分算法的图像重构[J]. 电子与信息学报, 2021, 43(7): 2105–2112. doi: 10.11999/JEIT200376 QIN Yali, MEI Jicai, REN Hongliang, et al. Image reconstruction based on Gaussian smooth compressed sensing fractional order total variation algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(7): 2105–2112. doi: 10.11999/JEIT200376
[3]	仲元红, 周宇杰, 张静, 等. 基于非局部先验的深度压缩感知图像重构网络[J]. 电子与信息学报, 2023, 45(2): 654–663. doi: 10.11999/JEIT211506 ZHONG Yuanhong, ZHOU Yujie, ZHANG Jing, et al. Deep compressive sensing image reconstruction network based on non-local prior[J]. Journal of Electronics &Information Technology, 2023, 45(2): 654–663. doi: 10.11999/JEIT211506
[4]	方澄, 李慧娟, 路稳, 等. 基于形态学自适应分块的高分辨SAR多特征增强算法[J]. 系统工程与电子技术, 2022, 44(2): 470–479. doi: 10.12305/j.issn.1001-506X.2022.02.15 FANG Cheng, LI Huijuan, LU Wen, et al. Multi-feature enhancement algorithm for high resolution SAR based on morphological auto-blocking[J]. Systems Engineering and Electronics, 2022, 44(2): 470–479. doi: 10.12305/j.issn.1001-506X.2022.02.15
[5]	MUN S and FOWLER J E. Block compressed sensing of images using directional transforms[C]. 2009 16th IEEE International Conference on Image Processing, Cairo, Egypt, 2009: 3021–3024.
[6]	何敬禄. 基于压缩感知的块稀疏信号重构和图像分块采样算法研究[D]. [硕士论文]. 广西大学, 2017. HE Jinglu. Research on block-sparse signal reconstruction and image block sampling algorithm based on compressive sensing[D]. [Master dissertation], Guangxi University, 2017.
[7]	MOHIMAN I H, BABAIE-ZADEH M, and JUTTEN C. A fast approach for overcomplete sparse decomposition based on smoothed l⁰ norm[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289–301. doi: 10.1109/TSP.2008.2007606
[8]	孙娜, 刘继文, 肖东亮. 基于BFGS拟牛顿法的压缩感知SL0重构算法[J]. 电子与信息学报, 2018, 40(10): 2408–2414. doi: 10.11999/JEIT170813 SUN Na, LIU Jiwen, and XIAO Dongliang. SL0 reconstruction algorithm for compressive sensing based on BFGS quasi newton method[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2408–2414. doi: 10.11999/JEIT170813
[9]	CANDES E J and TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203–4215. doi: 10.1109/TIT.2005.858979
[10]	ZHANG Li and ZHOU Weijun. Spectral gradient projection method for solving nonlinear monotone equations[J]. Journal of Computational and Applied Mathematics, 2006, 196(2): 478–484. doi: 10.1016/j.cam.2005.10.002
[11]	GU Yuejianan, PIAO Yan, and HUANG Yufu. Adaptive block compressed sensing algorithm based on integral imaging[C]. 2020 IEEE 3rd International Conference on Electronic Information and Communication Technology, Shenzhen, China, 2020: 85–88.
[12]	陈建, 苏凯雄, 杨秀芝, 等. 基于变分模型的块压缩感知重构算法[J]. 通信学报, 2016, 37(1): 100–109. doi: 10.11959/j.issn.1000-436x.2016011 CHEN Jian, SU Kaixiong, YANG Xiuzhi, et al. Reconstruction algorithm for block compressed sensing based on variation model[J]. Journal on Communications, 2016, 37(1): 100–109. doi: 10.11959/j.issn.1000-436x.2016011
[13]	YE Guodong, PAN Chen, HUANG Xiaoling, et al. An efficient pixel-level chaotic image encryption algorithm[J]. Nonlinear Dynamics, 2018, 94(1): 745–756. doi: 10.1007/s11071-018-4391-y
[14]	王玥, 周城, 熊承义, 等. 基于纹理自适应全变分滤波的图像分块压缩感知优化算法[J]. 计算机科学, 2016, 43(2): 307–310,315. doi: 10.11896/j.issn.1002-137X.2016.2.064 WANG Yue, ZHOU Cheng, XIONG Chengyi, et al. Enhanced block compressed sensing of images based on total variation using texture information[J]. Computer Science, 2016, 43(2): 307–310,315. doi: 10.11896/j.issn.1002-137X.2016.2.064
[15]	YE Xinrong and ZHU Weiping. Sparse channel estimation of pulse-shaping multiple-input-multiple-output orthogonal frequency division multiplexing systems with an approximate gradient l₂–Sl₀ reconstruction algorithm[J]. IET Communications, 2014, 8(7): 1124–1131. doi: 10.1049/iet-com.2013.0571
[16]	FANG Xiaofeng, ZHANG Jiangshe, and LI Yingqi. Sparse signal reconstruction based on multiparameter approximation function with smoothed l₀ norm[J]. Mathematical Problems in Engineering, 2014, 2014: 416542. doi: 10.1155/2014/416542
[17]	GENG Juan, WANG Laisheng, FU Aimin, et al. A smoothed rank function algorithm based Hyperbolic Tangent function for matrix completion[C]. 2012 International Conference on Machine Learning and Cybernetics, Xi’an, China, 2012: 1333–1338.
[18]	XIANG Jianhong, YUE Huihui, YIN Xiangjun, et al. A reweighted symmetric smoothed function approximating L₀-norm regularized sparse reconstruction method[J]. Symmetry, 2018, 10(11): 583. doi: 10.3390/sym10110583
[19]	张巍, 朱正为, 汪亮, 等. 一种A-HNSL0压缩感知SAR图像重建方法[J]. 电光与控制, 2020, 27(8): 28–32. doi: 10.3969/j.issn.1671-637X.2020.08.006 ZHANG Wei, ZHU Zhengwei, WANG Liang, et al. An A-HNSL0 compressed sensing based SAR image reconstruction method[J]. Electronics Optics &Control, 2020, 27(8): 28–32. doi: 10.3969/j.issn.1671-637X.2020.08.006
[20]	PANT J K, LU Wusheng, and ANTONIOU A. Unconstrained regularized l_p-norm based algorithm for the reconstruction of sparse signals[C]. 2011 IEEE International Symposium of Circuits and Systems, Rio de Janeiro, Brazil, 2011: 1740–1743.
[21]	ZHAO Hui, YE Hao, and WANG Ruyan. The construction of measurement matrices based on block weighing matrix in compressed sensing[J]. Signal Processing, 2016, 123: 64–74. doi: 10.1016/j.sigpro.2015.12.016
[22]	MAY R M. Simple mathematical models with very complicated dynamics[J]. Nature, 1976, 261(5560): 459–467. doi: 10.1038/261459a0
[23]	ZHANG Bo, XIAO Di, ZHANG Zhenyu, et al. Compressing encrypted images by using 2D compressed sensing[C]. 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems, Zhangjiajie, China, 2019: 1914–1919.
[24]	WU Rui, FU Yusheng, and LEI Jianmin. Adaptive multiscale block compressed sensing algorithm based on total variation[C]. 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference, Xi’an, China, 2018: 617–620.