Characteristic Analysis of Chaotic System Based on Binary-valued and Tri-valued Memristor Models
-
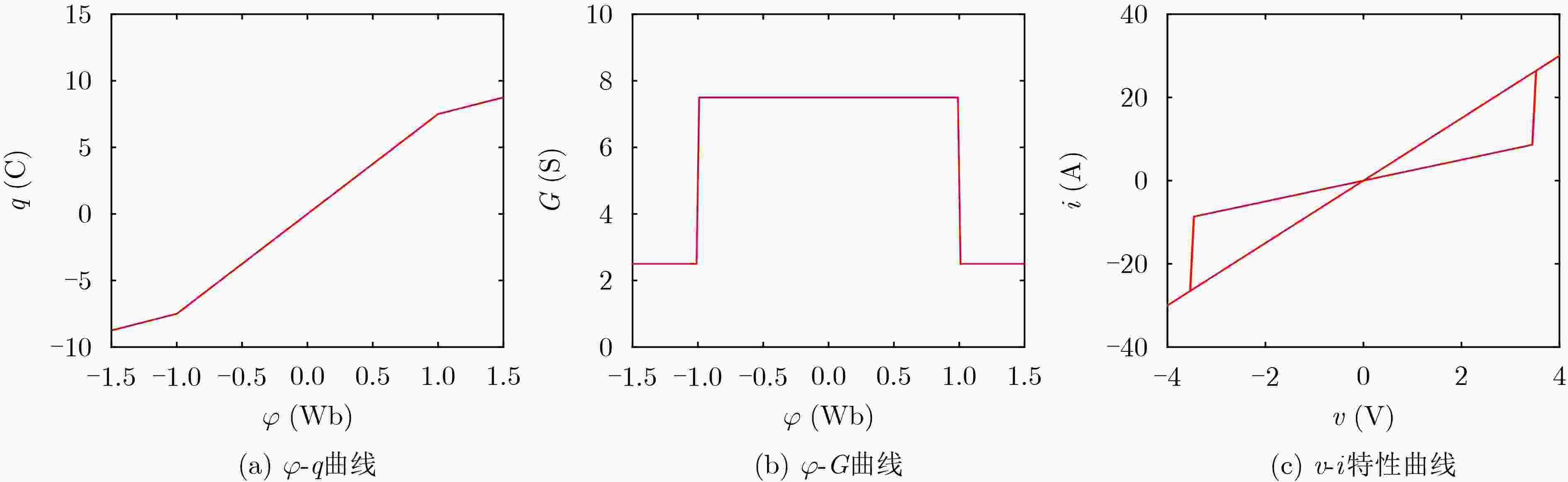
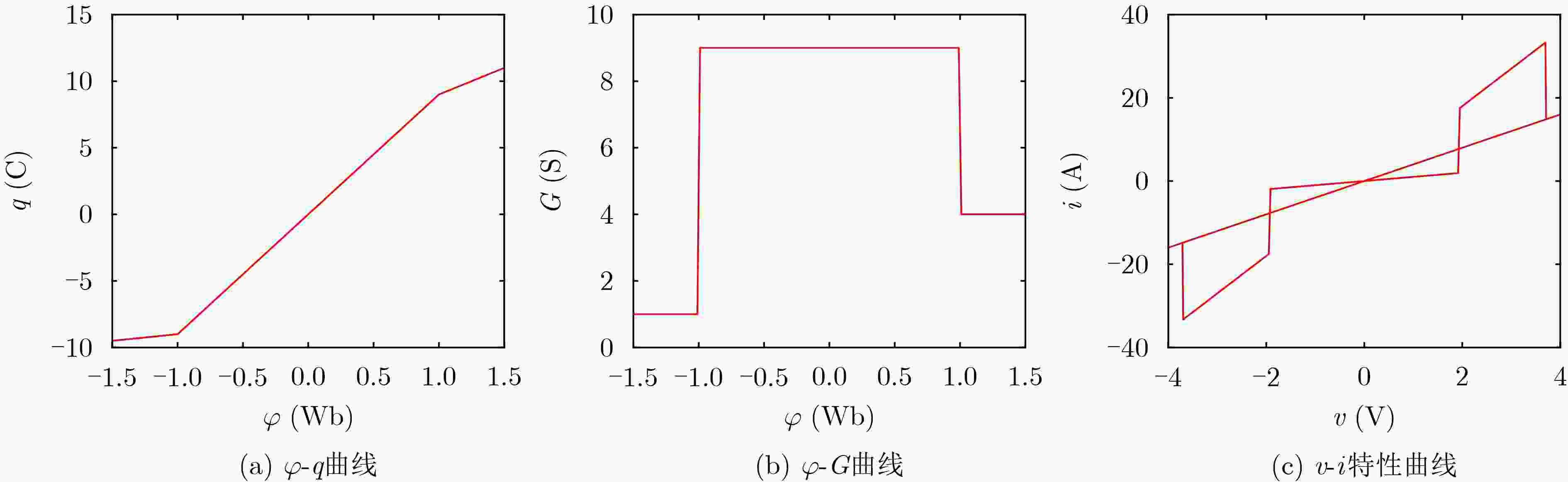
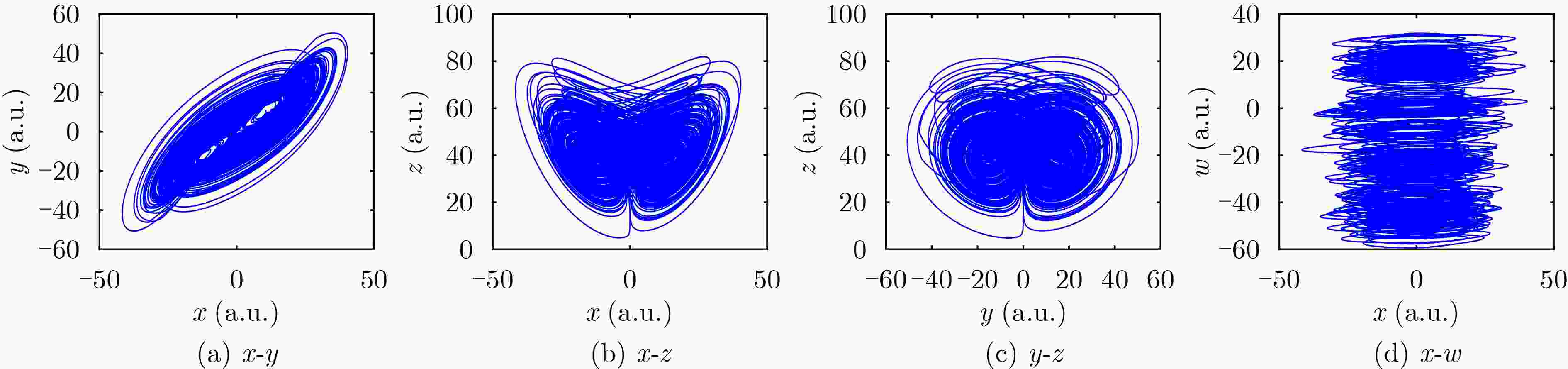
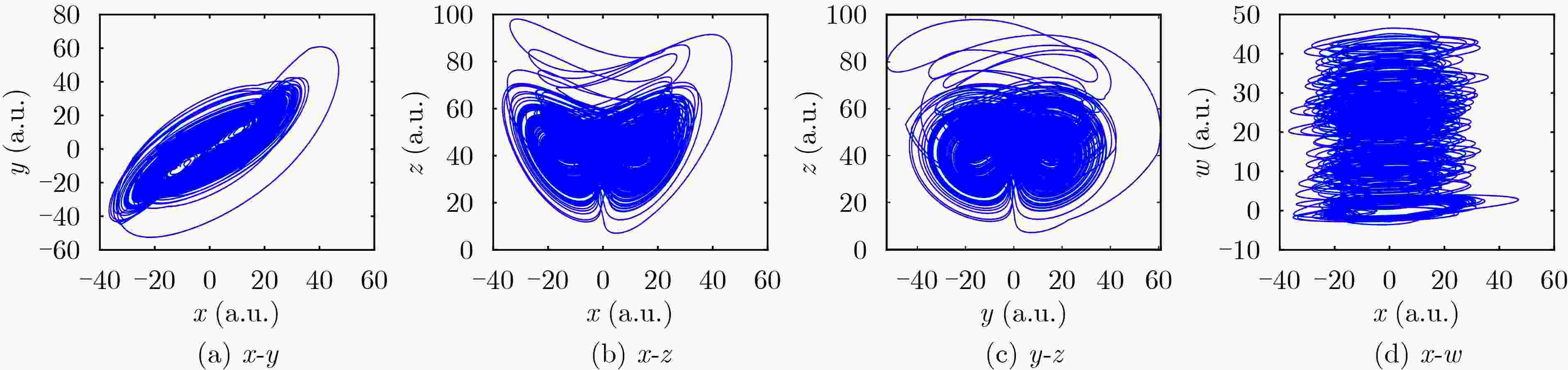
摘要: 近年来,基于忆阻器的非线性动力学问题备受关注。该文以二值和三值忆阻器为例分析了二值和多值忆阻器对于混沌系统动力特性的影响。首先,将二值忆阻器引入Chen系统,构建了一个4维的基于二值忆阻器的混沌系统(BMCS)。其次,使用三值忆阻器替换上述系统中的二值忆阻器,构建一个4维的基于三值忆阻器的混沌系统(TMCS)。通过理论分析与数值仿真,从多个角度对比了两个混沌系统之间的动力学特性差异,如Lyapunov指数、分岔图、系统的平衡点、系统稳定性、对初值的敏感性以及系统的复杂度分析等。结果表明,两个基于忆阻器的混沌系统都具有无穷多个平衡点,二者产生的吸引子均为隐藏吸引子,且都存在的暂态混沌现象,但三值忆阻混沌系统具有超混沌特性,且相比二值忆阻混沌系统具有更强的初值敏感性以及更大的参数取值区间。分析得出基于三值忆阻器构建的混沌系统比基于二值忆阻器的混沌系统能够产生更为复杂的动力学特性,混沌信号也更为复杂。Abstract: In recent years, nonlinear dynamics problems based on memristors have received much attention. In this paper, binary-valued and tri-valued memristors are used as examples to analyze the influence of binary-valued and multi-value memristors on the dynamic characteristics of chaotic systems. Firstly, the binary-valued memristor is introduced into the Chen system, and a four-dimensional Binary-valued Memristor-based Chaotic System(BMCS) is constructed. Secondly, a tri-valued memristor is used to replace the binary-valued memristor in the above system, and a four-dimensional Tri-valued Memristor-based Chaotic System(TMCS) is constructed. Through theoretical analysis and numerical simulation, the differences of dynamic characteristics between the two chaotic systems are compared from multiple perspectives, such as Lyapunov exponent, bifurcation diagram, equilibrium point of the system, system stability, sensitivity to initial value and system complexity analysis, etc. The results show that the two memristor-based chaotic systems have infinite equilibrium points, the attractors generated by both are hidden attractors, and both have transient chaotic phenomena, but the Tri-valued memristor chaotic system has Hyper-chaos, and has stronger initial value sensitivity than Binary-valued memristor chaotic system. Further, the Tri-valued memristor chaotic system has a larger parameter value interval than the Binary-valued memristor chaotic system to obtain chaotic sequences with sufficiently high complexity. Through analysis, it is concluded that the chaotic system based on Tri-valued memristor can generate more complex dynamic characteristics and more complex chaotic signal than the chaotic system based on binary-valued memristor.
-
Key words:
- Binary-valued memristor /
- Tri-valued memristor /
- Hyper-chaos /
- Hidden attractors /
- System complexity
-
表 1 混沌系统的Lyapunov指数及Lyapunov维数
混沌系统 公式 LE1 LE2 LE3 LE4 DL 超混沌 BMCS 式(5) 2.3090 –0.0017 –0.0795 –18.2281 3.1222 否 TMCS 式(6) 2.4818 0.1578 0.0017 –18.6413 3.1417 是 表 2 序列相关性的对照比较
混沌系统 X1,X2的相关性 Y1,Y2的相关性 Z1,Z2的相关性 W1,W2的相关性 BMCS –0.0122 –0.0137 –0.0207 0.1530 TMCS –0.0085 –0.0068 0.0017 –0.0055 表 3 不同参数c对应的Lyapunov指数值
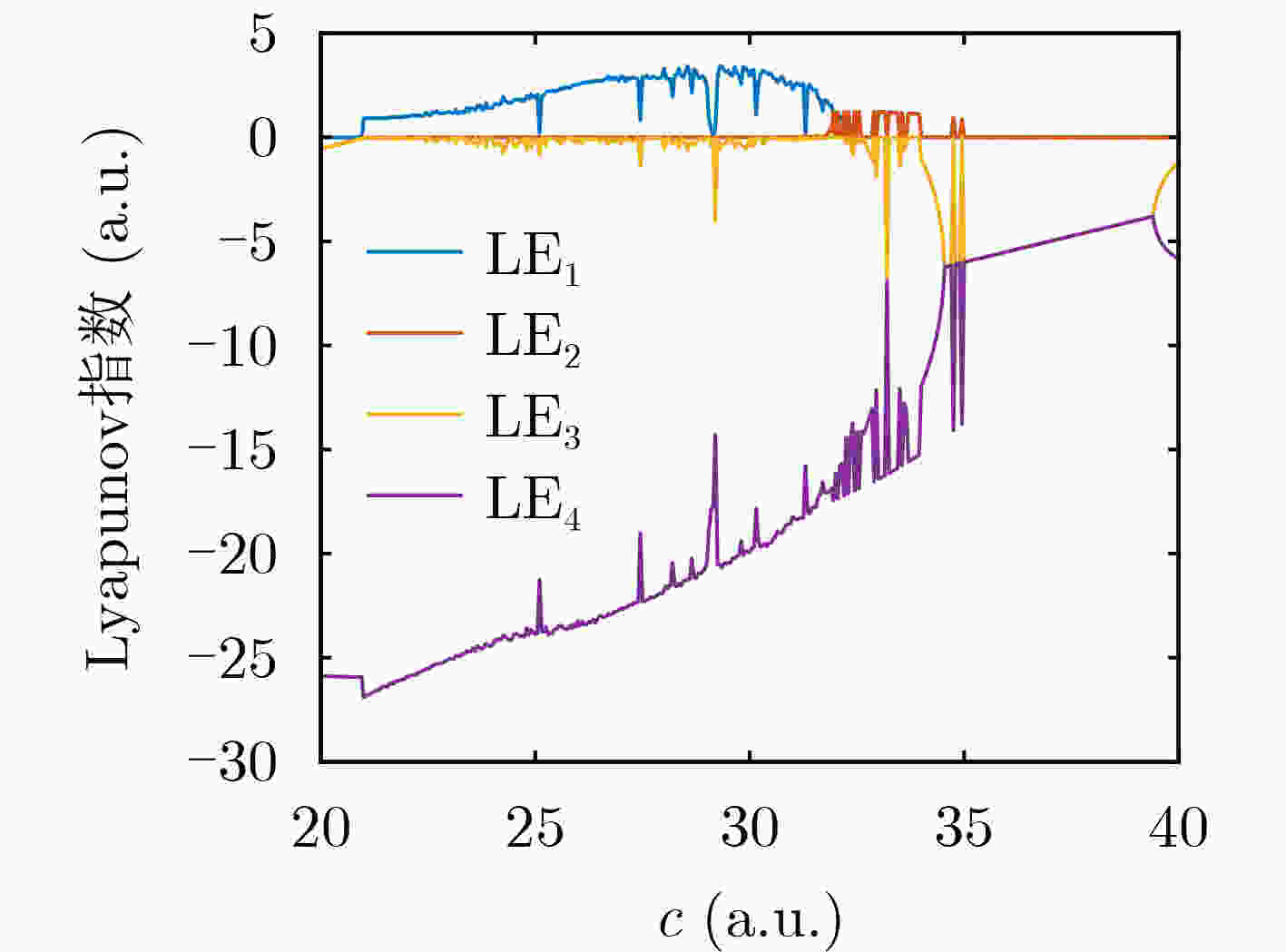
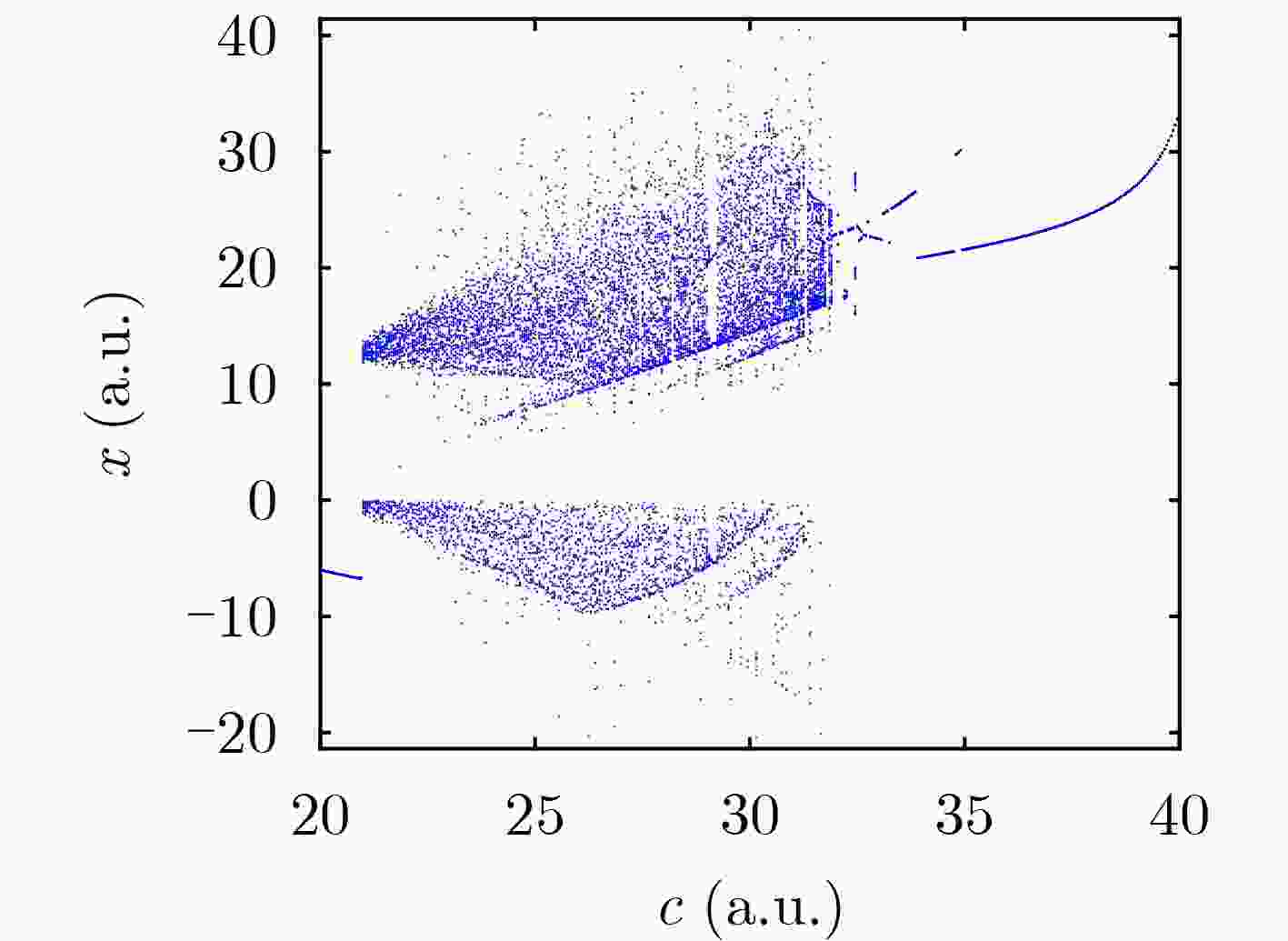
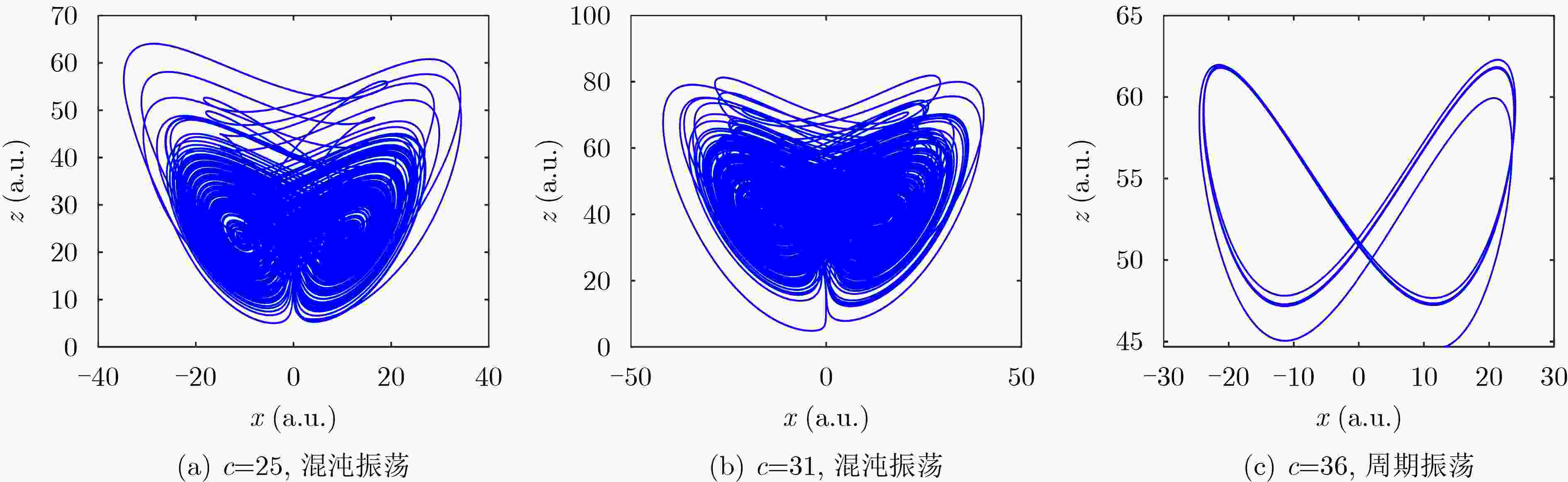
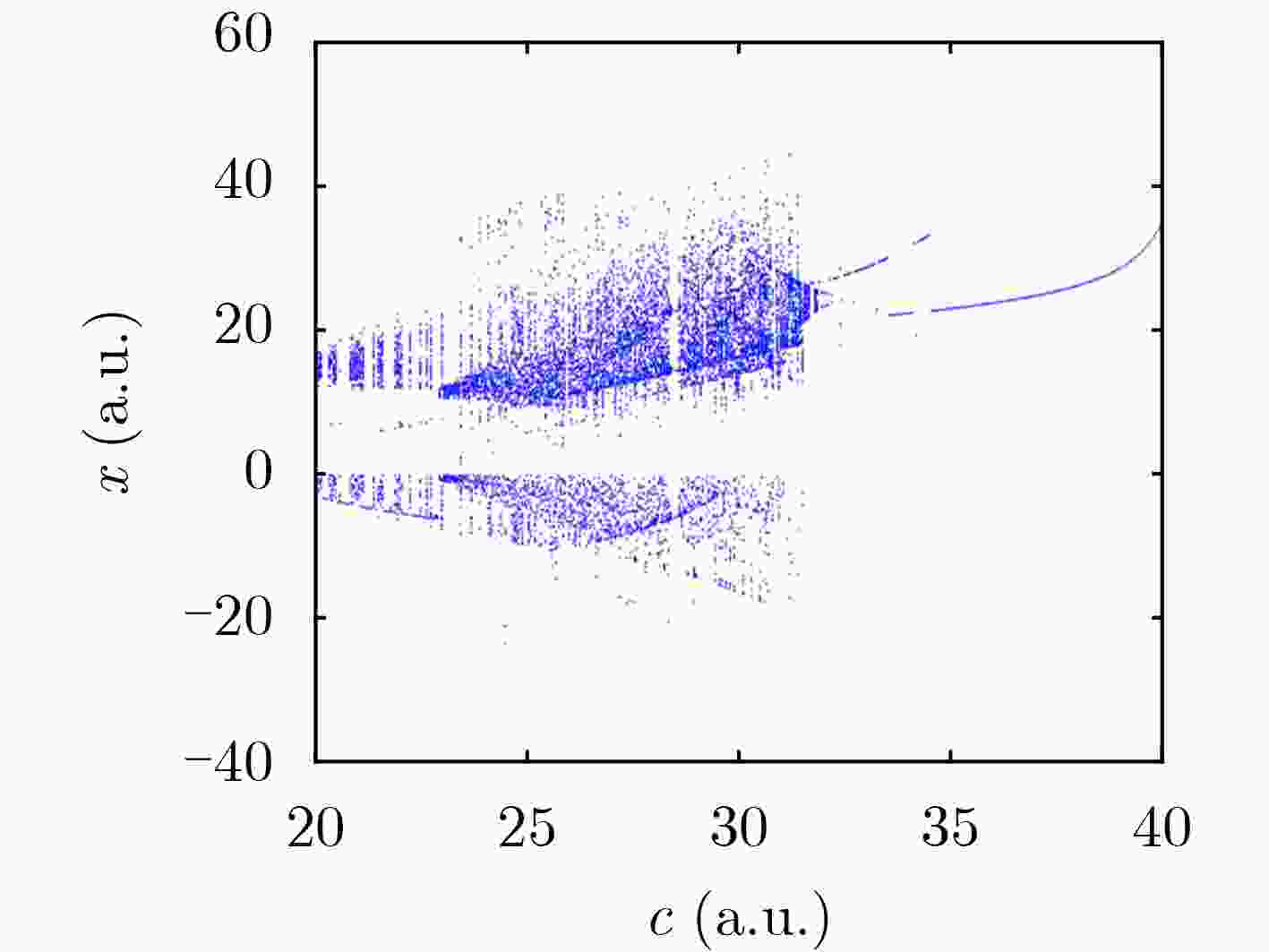
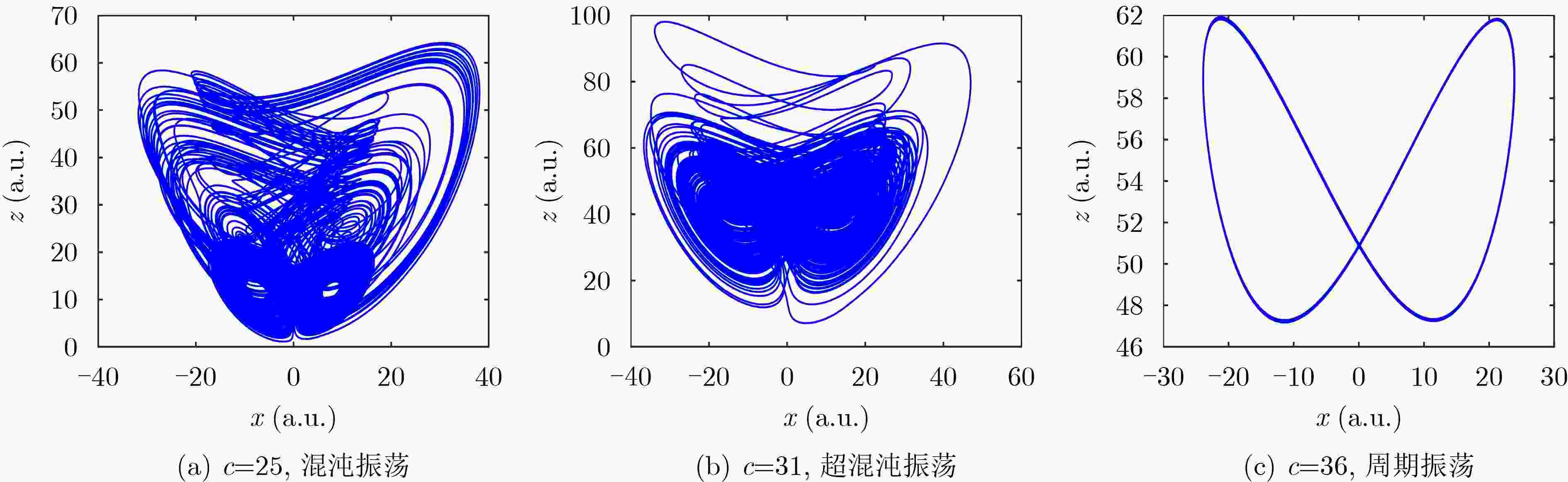
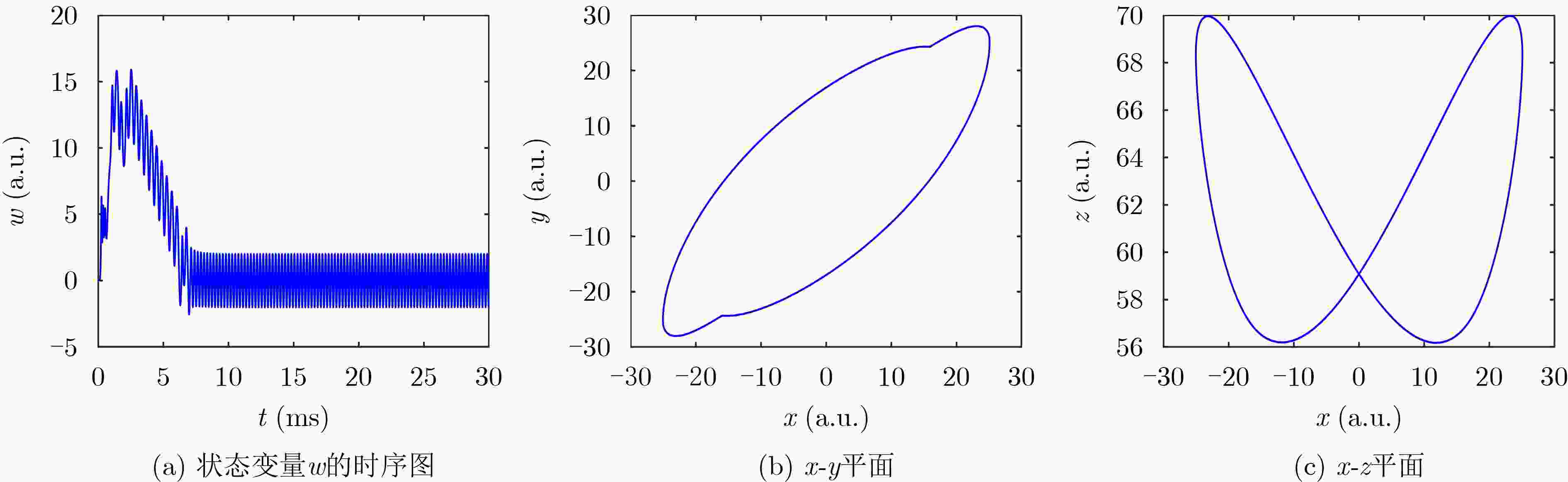
参数c LE1 LE2 LE3 LE4 系统状态 25 2.3090 0.0007 –0.0329 –23.8567 混沌 31 2.3090 –0.0017 –0.0795 –18.2281 混沌 36 0.0068 –0.0111 –5.4995 –5.4962 周期 表 4 不同参数下TMCS对应的Lyapunov指数值
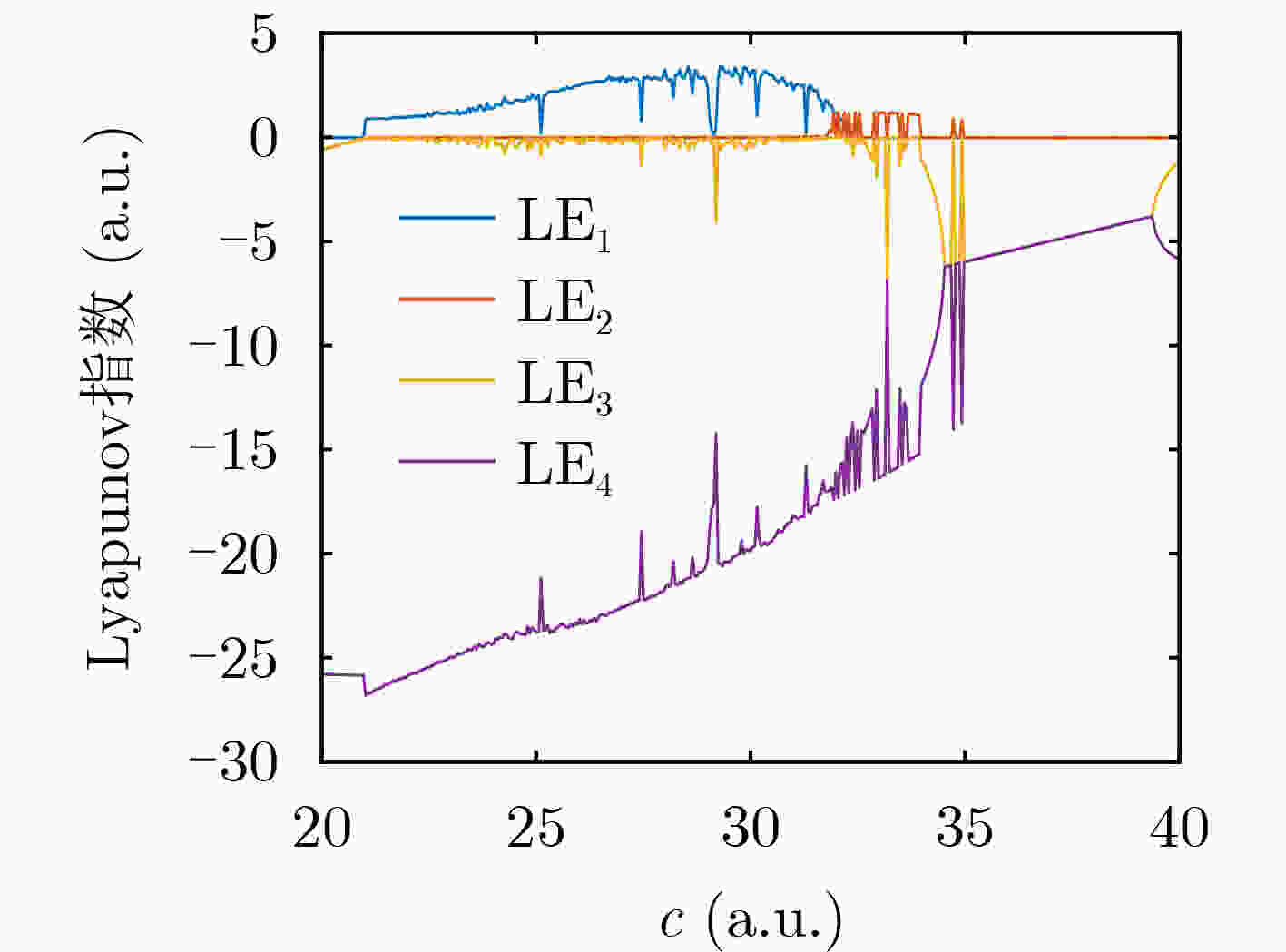
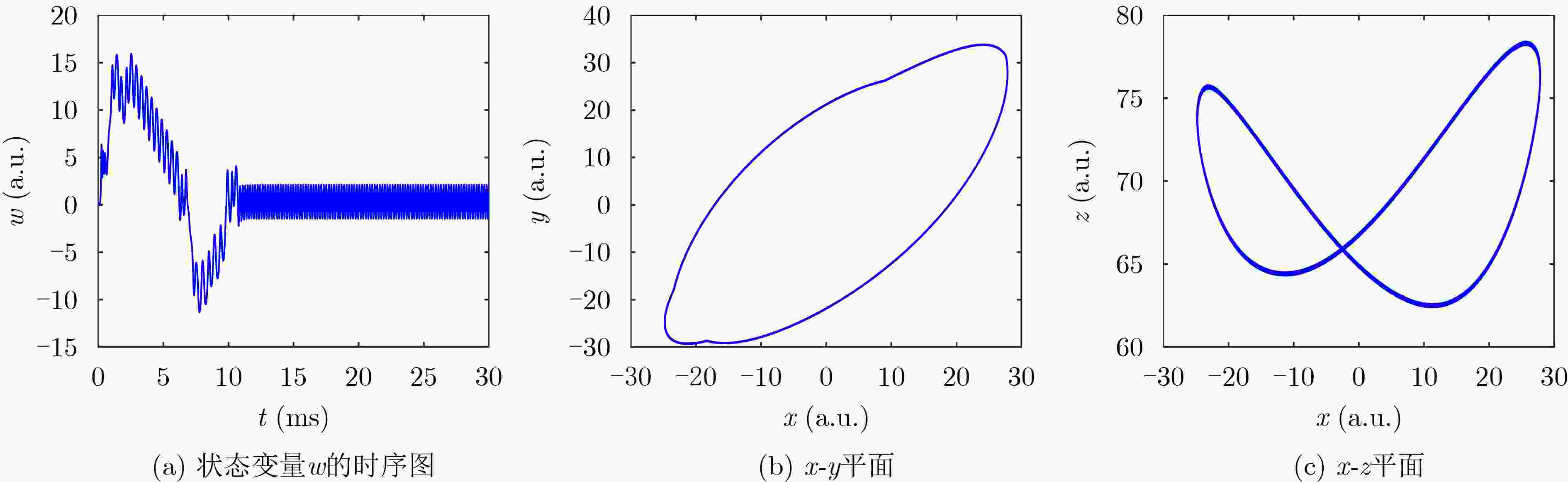
参数c LE1 LE2 LE3 LE4 系统状态 25 2.2273 –0.0066 –0.0628 –18.6413 混沌 31 2.4818 0.1578 0.0017 –18.6413 超混沌 36 0.0087 –0.0090 –5.5039 –5.4958 周期 -
[1] WANG Xiaoyuan, GAO Meng, IU H H C, et al. Tri-valued memristor-based hyper-chaotic system with hidden and coexistent attractors[J]. Chaos, Solitons & Fractals, 2022, 159: 112177. doi: 10.1016/j.chaos.2022.112177 [2] GUO Mei, YANG Wenyan, XUE Youbao, et al. Multistability in a physical memristor-based modified Chua’s circuit[J]. Chaos, 2019, 29(4): 043114. doi: 10.1063/1.5089293 [3] ZHANG Xinrui, WANG Xiaoyuan, GE Zhenyu, et al. A novel memristive neural network circuit and its application in character recognition[J]. Micromachines, 2022, 13(12): 2074. doi: 10.3390/mi13122074 [4] ZHOU Lili and TAN Fei. A chaotic secure communication scheme based on synchronization of double-layered and multiple complex networks[J]. Nonlinear Dynamics, 2019, 96(2): 869–883. doi: 10.1007/s11071-019-04828-7 [5] YANG Sen, TONG Xiaojun, WANG Zhu, et al. Efficient color image encryption algorithm based on 2D coupled chaos and multi-objective optimized S-box[J]. Physica Scripta, 2022, 97(4): 045204. doi: 10.1088/1402-4896/ac59fa [6] WANG Xiaoyuan, GAO Meng, MIN Xiaotao, et al. On the use of memristive hyperchaotic system to design color image encryption scheme[J]. IEEE Access, 2020, 8: 182240–182248. doi: 10.1109/ACCESS.2020.3027480 [7] ITOH M and CHUA L O. Memristor oscillators[J]. International Journal of Bifurcation and Chaos, 2008, 18(11): 3183–3206. doi: 10.1142/S0218127408022354 [8] TAN Qiwei, ZENG Yicheng, and LI Zhijun. A simple inductor-free memristive circuit with three line equilibria[J]. Nonlinear Dynamics, 2018, 94(3): 1585–1602. doi: 10.1007/s11071-018-4443-3 [9] 秦铭宏, 赖强, 吴永红. 具有无穷共存吸引子的简单忆阻混沌系统的分析与实现[J]. 物理学报, 2022, 71(16): 160502. doi: 10.7498/aps.71.20220593QIN Minghong, LAI Qiang, and WU Yonghong. Analysis and implementation of simple four-dimensional memristive chaotic system with infinite coexisting attractors[J]. Acta Physics Sinica, 2022, 71(16): 160502. doi: 10.7498/aps.71.20220593 [10] WANG Xiaoyuan, YU Jun, JIN Chenxi, et al. Chaotic oscillator based on memcapacitor and meminductor[J]. Nonlinear Dynamics, 2019, 96(1): 161–173. doi: 10.1007/s11071-019-04781-5 [11] MIN Xiaotao, WANG Xiaoyuan, ZHOU Pengfei, et al. An optimized memristor-based hyperchaotic system with controlled hidden attractors[J]. IEEE Access, 2019, 7: 124641–124646. doi: 10.1109/ACCESS.2019.2938183 [12] WANG Xiaoyuan, MIN Xiaotao, ZHOU Pengfei, et al. Hyperchaotic circuit based on memristor feedback with multistability and symmetries[J]. Complexity, 2020, 2020: 2620375. doi: 10.1155/2020/2620375 [13] LAI Qiang, WAN Zhiqiang, KUATE P D K, et al. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit[J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 89: 105341. doi: 10.1016/j.cnsns.2020.105341 [14] WANG Chunhua, ZHOU Ling, and WU Renping. The design and realization of a hyper-chaotic circuit based on a flux-controlled memristor with linear memductance[J]. Journal of Circuits, Systems and Computers, 2018, 27(3): 1850038. doi: 10.1142/S021812661850038X [15] 张贵重, 全旭, 刘嵩. 一个具有超级多稳定性的忆阻混沌系统的分析与FPGA实现[J]. 物理学报, 2022, 71(24): 240502. doi: 10.7498/aps.71.20221423ZHANG Guizhong, QUAN Xu, and LIU Song. Analysis and FPGA implementation of memristor chaotic system with extreme multistability[J]. Acta Physica Sinica, 2022, 71(24): 240502. doi: 10.7498/aps.71.20221423 [16] WANG Xiaoyuan, ZHOU Pengfei, JIN Chenxi, et al. Mathematic modeling and circuit implementation on multi-valued memristor[C]. 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 2020: 1–5. [17] WANG Xiaoyuan, ZHANG Xue, and GAO Meng. A novel voltage-controlled tri-valued memristor and its application in chaotic system[J]. Complexity, 2020, 2020: 6949703. doi: 10.1155/2020/6949703 [18] CHEN Guanrong and UETA T. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999, 9(7): 1465–1466. doi: 10.1142/S0218127499001024 [19] HUA Zhongyun and ZHOU Yicong. Dynamic parameter-control chaotic system[J]. IEEE Transactions on Cybernetics, 2016, 46(12): 3330–3341. doi: 10.1109/TCYB.2015.2504180 [20] HU Gang, WANG Kejun, and LIU Liangliang. Detection line spectrum of ship radiated noise based on a new 3D chaotic system[J]. Sensors, 2021, 21(5): 1610. doi: 10.3390/s21051610 -





 下载:
下载:



 下载:
下载:
