A Study of Local Differential Privacy Mechanisms Based on Federated Learning
-
摘要: 联邦学习与群体学习作为当前热门的分布式机器学习范式,前者能够保护用户数据不被第三方获得的前提下在服务器中实现模型参数共享计算,后者在无中心服务器的前提下利用区块链技术实现所有用户同等地聚合模型参数。但是,通过分析模型训练后的参数,如深度神经网络训练的权值,仍然可能泄露用户的隐私信息。目前,在联邦学习下运用本地化差分隐私(LDP)保护模型参数的方法层出不穷,但皆难以在较小的隐私预算和用户数量下缩小模型测试精度差。针对此问题,该文提出正负分段机制(PNPM),在聚合前对本地模型参数进行扰动。首先,证明了该机制满足严格的差分隐私定义,保证了算法的隐私性;其次分析了该机制能够在较少的用户数量下保证模型的精度,保证了机制的有效性;最后,在3种主流图像分类数据集上与其他最先进的方法在模型准确性、隐私保护方面进行了比较,表现出了较好的性能。Abstract: Federated Learning and swarm Learning, as currently popular distributed machine learning paradigms, the former enables shared computation of model parameters in servers while protecting user data from third parties, while the latter uses blockchain technology to aggregate model parameters equally for all users without a central server. However, by analyzing the parameters after model training, such as the weights of deep neural network training, it is still possible to leak the user's private information. At present, there are several methods for protecting model parameters utilizing Local Differential Privacy (LDP) in federated learning, however it is challenging to reduce the gap in model testing accuracy when there is a limited privacy budget and user base. To solve this problem, a Positive and Negative Piecewise Mechanism (PNPM) is proposed, which perturbs the local model parameters before aggregation. First, it is proved that the mechanism satisfies the strict definition of differential privacy and ensures the privacy of the algorithm; Secondly, it is analyzed that the mechanism can ensure the accuracy of the model under a small number of users and ensure the effectiveness of the mechanism; Finally, it is compared with other state-of-the-art methods in terms of model accuracy and privacy protection on three mainstream image classification datasets and shows a better performance.
-
Key words:
- Privacy preserving /
- Federated learning /
- Local Differential Privacy (LDP) /
- Blockchain
-
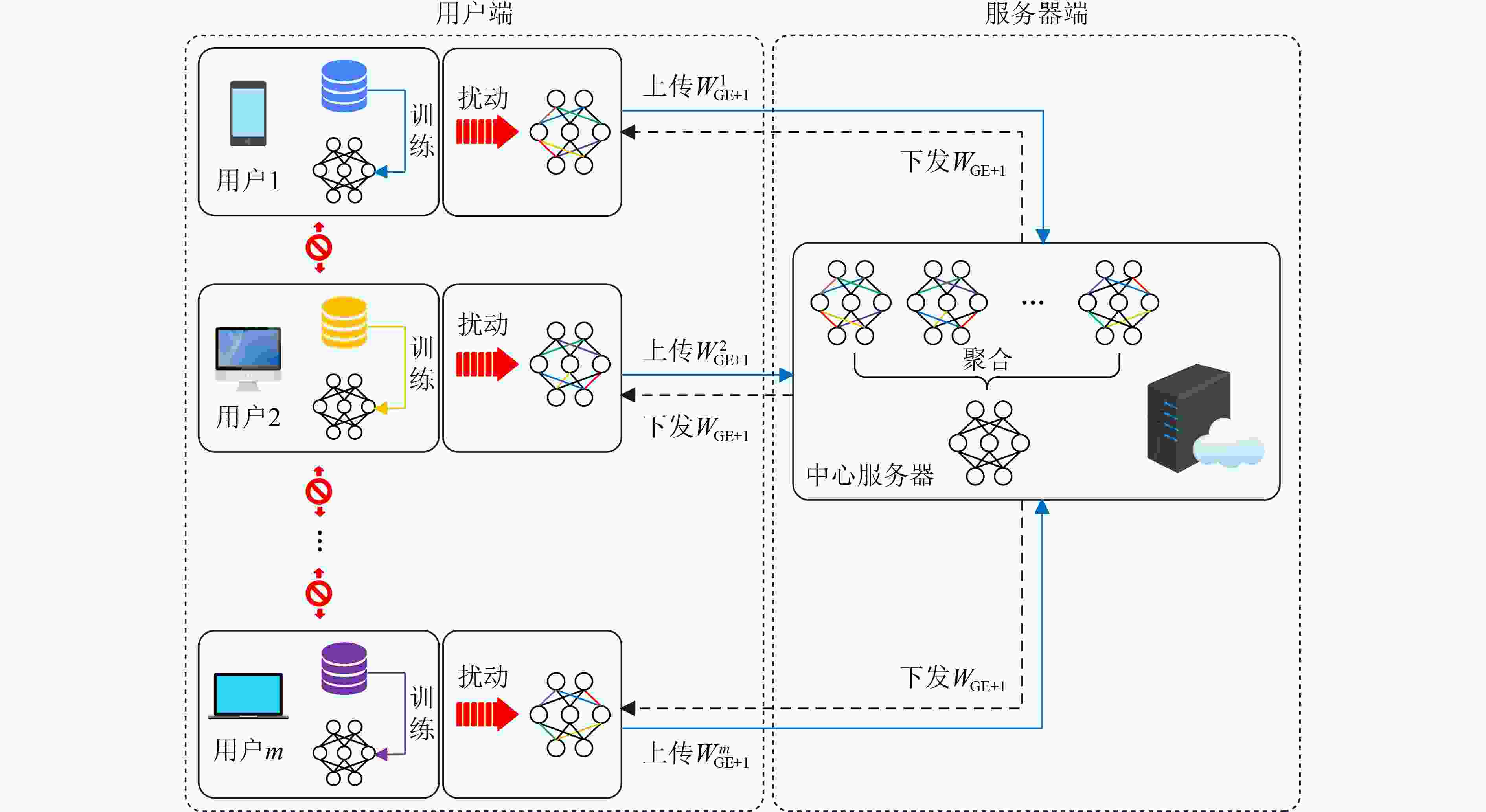
算法1 结合本地化差分隐私保护的联邦学习算法 输入:n是本地用户的数量;B是本地mini-batch大小;LE为本
地迭代数量;GE为全局迭代数量;γ为学习率;Fr为用户比率。(1)服务器更新 (2)初始化全局模型${W_0}$; (3)发送给用户 ; (4)进行GE轮迭代 (5) 随机选取$m = {\text{Fr}} \cdot n$个本地用户; (6) 收集发送给服务器的$m$个更新后的模型参数; (7) # 聚合并更新全局模型${W_{{\text{GE}}}}$; (8) for 每个相同位置权重$w \in \left\{ {W_{{\text{GE}}}^m} \right\}$ do (9) $w\stackrel{ }{\leftarrow }\dfrac{1}{m}\displaystyle\sum w$; (10) 发送给用户 ; (11)本地更新 (12)接受发送给用户的全局模型${W_{{\text{GE}}}}$,用户数量$m$; (13)for 每个本地用户$s \in m$ do (14) $ {W}_{\text{GE}+1}^{s}\stackrel{ }{\leftarrow }{W}_{\text{GE}} $; (15) 本地进行LE轮迭代 (16) for 每个批$b \in B$ do (17) $ {W}_{\text{GE}+1}^{s}\stackrel{ }{\leftarrow }{W}_{\text{GE}+1}^{s}-\gamma \nabla L\left({W}_{\text{GE}+1}^{s};b\right) $; (18) # 对本地模型参数进行扰动 (19) for 每个$w \in W_{{\text{GE}} + 1}^s$ do (20) $w\stackrel{ }{\leftarrow }\left|w\right|\cdot \mathrm{PNPM}\left(\dfrac{w}{\left|w\right|}\right)$; (21) 发送给服务器; (22)返回。 算法2 正负分段机制PNPM 输入:$t \in \left\{ { - 1,1} \right\}$和隐私预算$\varepsilon $。 输出:${t^*} \in \left[ { - C, - 1\left] \cup \right[1,C} \right]$。 (1)在$ \left[\mathrm{0,1}\right] $$\left[ {0,1} \right]$内均匀地取一个随机数$x$; (2)如果$x < \dfrac{ {{\rm{e}}}^{\epsilon } }{ {{\rm{e}}}^{\epsilon}+1}$,那么 (3) ${t^*}$在$\left[ {l\left( t \right),r\left( t \right)} \right]$上均匀取一个随机数; (4)否则 (5) ${t^*}$在$\left[ { - r\left( t \right), - l\left( t \right)} \right]$上均匀取一个随机数; (6)返回${t^*}$。 表 1
$t = - 1$ 或$t = 1$ 扰动值${t^*}$ 的概率密度函数值$t = - 1$ $t = 1$ $ - r\left( t \right) \le y \le - l\left( t \right)$ $l\left( t \right) \le y \le r\left( t \right)$ $ - r\left( t \right) \le y \le - l\left( t \right)$ $l\left( t \right) \le y \le r\left( t \right)$ ${\text{pdf(}}{t^*} = y|t)$ $ \dfrac{{\text{e}}^{2\varepsilon }-{\text{e}}^{\varepsilon }}{4{\left({\text{e}}^{\varepsilon }+1\right)}^{ }} $ $ \dfrac{{\text{e}}^{\varepsilon }-1}{4{\left({\text{e}}^{\varepsilon }+1\right)}^{ }} $ $ \dfrac{{\text{e}}^{\varepsilon }-1}{4{\left({\text{e}}^{\varepsilon }+1\right)}^{ }} $ $ \dfrac{{\text{e}}^{2\varepsilon }-{\text{e}}^{\varepsilon }}{4{\left({\text{e}}^{\varepsilon }+1\right)}^{ }} $ 表 2 在不改变卷积核参数正负的前提下,两种赋值所能得到的精度(%)
数据集 每个权重绝对值都为0.5 每个权重在(–1,0)∪(0,1)上随机取值(20次随机中的最大精度) 未做处理的模型原精度 MNIST 78.67 89.10 98.98 Fashion-MNIST 75.26 72.83 89.89 Cifar-10 28.00 27.18 71.83 -
[1] WANG Shuai, KANG Bo, MA Jinlu, et al. A deep learning algorithm using CT images to screen for Corona virus disease (COVID-19)[J]. European Radiology, 2021, 31(8): 6096–6104. doi: 10.1007/s00330-021-07715-1 [2] MCMAHAN H B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[EB/OL]. https://doi.org/10.48550/arXiv.1602.05629, 2016. [3] 杨强. AI与数据隐私保护: 联邦学习的破解之道[J]. 信息安全研究, 2019, 5(11): 961–965. doi: 10.3969/j.issn.2096-1057.2019.11.003YANG Qiang. AI and data privacy protection: The way to federated learning[J]. Journal of Information Security Research, 2019, 5(11): 961–965. doi: 10.3969/j.issn.2096-1057.2019.11.003 [4] WARNAT-HERRESTHAL S, SCHULTZE H, SHASTRY K L, et al. Swarm Learning for decentralized and confidential clinical machine learning[J]. Nature, 2021, 594(7862): 265–270. doi: 10.1038/s41586-021-03583-3 [5] SONG Congzheng, RISTENPART T, and SHMATIKOV V. Machine learning models that remember too much[C]. 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 587–601. [6] FREDRIKSON M, JHA S, and RISTENPART T. Model inversion attacks that exploit confidence information and basic countermeasures[C]. 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, USA, 2015: 1322–1333. [7] SUN Lichao, QIAN Jianwei, and CHEN Xun. LDP-FL: Practical private aggregation in federated learning with local differential privacy[C]. The Thirtieth International Joint Conference on Artificial Intelligence, Montreal, Canada, 2021: 1571–1578. [8] PAPERNOT N, ABADI M, ERLINGSSON Ú, et al. Semi-supervised knowledge transfer for deep learning from private training data[C]. 5th International Conference on Learning Representations, Toulon, France, 2017. [9] PAPERNOT N, MCDANIEL P, SINHA A, et al. SoK: Security and privacy in machine learning[C]. 2018 IEEE European Symposium on Security and Privacy, London, UK, 2018: 399–414. [10] TRAMÈR F, ZHANG Fan, JUELS A, et al. Stealing machine learning models via prediction APIs[C]. The 25th USENIX Conference on Security Symposium, Austin, USA, 2016: 601–618. [11] WANG Binghui and GONG N Z. Stealing hyperparameters in machine learning[C]. 2018 IEEE Symposium on Security and Privacy, San Francisco, USA, 2018: 36–52. [12] LYU Lingjuan, YU Han, MA Xingjun, et al. Privacy and robustness in federated learning: Attacks and defenses[J]. IEEE Transactions on Neural Networks and Learning Systems, To be published. doi: 10.1109/TNNLS.2022.3216981 [13] SUN Lichao and LYU Lingjuan. Federated model distillation with noise-free differential privacy[C]. The Thirtieth International Joint Conference on Artificial Intelligence, Montreal, Canada, 2021: 1563–1570. [14] MCMAHAN H B, RAMAGE D, TALWAR K, et al. Learning differentially private recurrent language models[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [15] GEYER R C, KLEIN T, and NABI M. Differentially private federated learning: A client level perspective[EB/OL]. https://doi.org/10.48550/arXiv.1712.07557, 2017. [16] NGUYÊN T T, XIAO Xiaokui, YANG Yin, et al. Collecting and analyzing data from smart device users with local differential privacy[EB/OL]. https://doi.org/10.48550/arXiv.1606.05053, 2016. [17] DUCHI J C, JORDAN M I, and WAINWRIGHT M J. Local privacy, data processing inequalities, and statistical minimax rates[EB/OL]. https://doi.org/10.48550/arXiv.1302.3203, 2013. [18] WANG Ning, XIAO Xiaokui, YANG Yin, et al. Collecting and analyzing multidimensional data with local differential privacy[C]. 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 2019: 638–649, [19] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791 [20] XIAO Han, RASUL K, and VOLLGRAF R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms[EB/OL]. https://doi.org/10.48550/arXiv.1708.07747, 2017. [21] KRIZHEVSKY A. Learning multiple layers of features from tiny images[R]. Technical Report TR-2009, 2009. [22] 邱晓慧, 杨波, 赵孟晨, 等. 联邦学习安全防御与隐私保护技术研究[J]. 计算机应用研究, 2022, 39(11): 3220–3231. doi: 10.19734/j.issn.1001-3695.2022.03.0164QIU Xiaohui, YANG Bo, ZHAO Mengchen, et al. Survey on federated learning security defense and privacy protection technology[J]. Application Research of Computers, 2022, 39(11): 3220–3231. doi: 10.19734/j.issn.1001-3695.2022.03.0164 [23] ZHU Ligeng, LIU Zhijian, and HAN Song. Deep leakage from gradients[C]. The 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 1323. [24] YANG Ziqi, ZHANG Jiyi, CHANG E C, et al. Neural network inversion in adversarial setting via background knowledge alignment[C]. The 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 2019: 225–240. [25] ZHANG Yuheng, JIA Ruoxi, PEI Hengzhi, et al. The secret revealer: Generative model-inversion attacks against deep neural networks[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 250–258, [26] BHOWMICK A, DUCHI J, FREUDIGER J, et al. Protection against reconstruction and its applications in private federated learning[EB/OL]. https://doi.org/10.48550/arXiv.1812.00984, 2018. [27] TRUEX S, LIU Ling, CHOW K H, et al. LDP-fed: Federated learning with local differential privacy[C]. The Third ACM International Workshop on Edge Systems, Analytics and Networking, Heraklion, Greece, 2020: 61–66. [28] SHOKRI R, STRONATI M, SONG Congzheng, et al. Membership inference attacks against machine learning models[C]. 2017 IEEE Symposium on Security and Privacy (SP), San Jose, USA, 2017: 3–18. -





 下载:
下载:
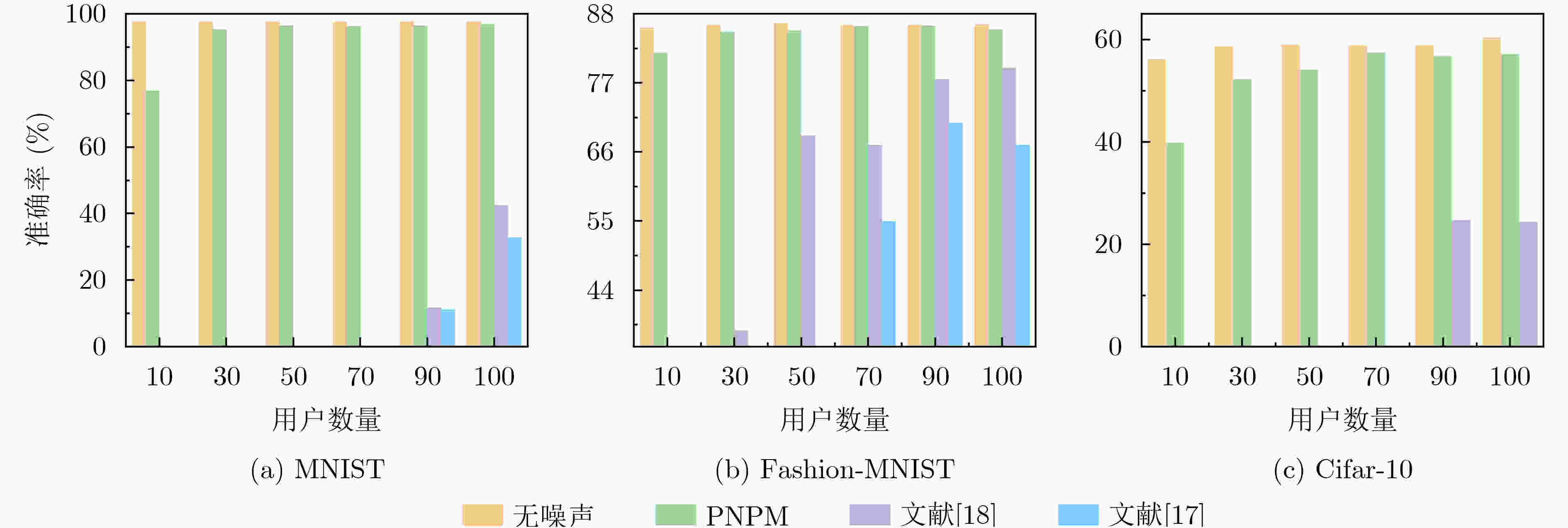





 下载:
下载:
