An Off-Grid DOA Estimation Based on Iterative Adaptive Approach
-
摘要: 针对真实信源位置与字典网格不匹配导致波达角估计(DOA)误差过大的问题，该文提出一种基于修正迭代自适应(IAA)功率谱算法的离网格(Off-Grid)DOA估计方法(OGIAA)。该方法首先通过修正IAA方法得到信号功率谱，读出功率峰值的对应网格角度作为粗估计结果，再利用平方误差代价函数，将代价函数2阶泰勒展开并最小化得到初始偏移量，最后交替优化功率分量和偏移量，实现高精度的离网格DOA估计。理论分析和仿真结果表明，该方法实现过程简单，无正则化参数影响，能准确估计出偏移网格的信源角度，在高阵列自由度的非均匀阵列上也同样具备高估计精度。Abstract: According to the problems that the mismatch between the real source location and the dictionary grid leads to the great error of Direction Of Arrival (DOA), an Off-Grid DOA estimation based on modified Iterative Adaptive Approach (IAA) is proposed (OGIAA). Firstly, the signal power spectrum obtained by the IAA is modified, and the corresponding grid angle of the peak power is read out as the coarse estimation results. Then, the square error cost function is expanded to the second order Taylor expansion and minimized to obtain the initial offset. Finally, the power component and offset are optimized alternately to achieve high precision off grid DOA estimation. Theoretical analysis and simulation results show that the implementation process of this method is simple, and it can accurately estimate the source angle of the migration grid without regularization parameters. It also has higher estimation accuracy on non-uniform arrays with more degrees of freedom.
-
1. 引言
波达方向估计(Direction Of Arrival, DOA)在雷达、通信、电子对抗、生物医学等领域有着广泛的应用。在现有的DOA估计方法中，基于稀疏重构的估计算法适用于非均匀阵列，能估计出比阵元数更多的信源个数，并且在低信噪比、低快拍、相干信源条件下具有优良的性能，因此得到了广大学者的关注[1-20]。
基于稀疏重构的DOA估计方法需要选择一个稀疏度量，在预定义的离散字典网格上进行信号的重构。一些方法利用正则化系数综合重构精度与稀疏程度，这往往会导致估计结果精度无法保证[3,4]。为了消除正则化系数的干扰，一系列无参数的估计方法被提出，如基于稀疏迭代的协方差估计(SParse Iterative Covariance based Estimation, SPICE)、迭代自适应(Iterative Adaptive Approach, IAA)、基于似然的稀疏参数估计(LIkelihood-based Estimation of Sparse parameters, LIKES)等[5-7]，这些方法能在预定义的网格上重构信号，然而实际上待估计信源的位置往往不会正好定位在网格上，导致估计结果误差较大。
为了解决网格与信源位置不匹配的问题，一类方法是提高网格的密集度，但这会导致算法复杂度急剧上升[8]；另一类方法是自适应的网格细化方法，徐文先等人[9]在IAA算法的估计的基础上细化网格，进行自适应的字典校正，能准确估计出偏离网格的信源角度，但是细化网格会带来较大运算负担，并且当网格间的相关度过高时，根据有限等距性质(Restricted Isometry Property, RIP)准则，此时算法的估计能力反而大大降低[10]。针对该问题，近年来国内外学者提出了基于偏移量的离网格稀疏重构估计方法[11-15]。Gretsistas等人[11]基于正交匹配的原则提出了同步正交匹配追踪(Simultaneous Orthogonal Matching Pursuit, SOMP)方法，交替优化信号分量和网格偏移量，实现了离网格的DOA估计，但是其计算量过高，并且部分情况下精度无法保证；Yang等人[12]提出了一种离网稀疏贝叶斯推理(Off-Grid Sparse Bayesian Inference, OGSBI)的方法。在OGSBI方法基础上，一系列基于贝叶斯框架内的估计算法被提出，如Wu等人[13]提出的基于期望最大化的改进稀疏贝叶斯推理方法等。然而上述方法大多涉及非凸优化，只能保证局部收敛，并且具有较大计算复杂度。Ma等人[14]提出了一种基于迭代相位偏移校正的估计方法(Iterative Phase Offset Correction, IPOC)，该方法利用虚拟阵的等效单快拍接收数据结构进行DOA估计，应用在稀疏阵上能在增大阵列自由度的同时减小算法复杂度，但应用在均匀阵时估计精度受限；王洪雁等人[15]提出了一种基于协方差矩阵重构的离网格DOA方法，但其功率求解涉及凸优化问题，具有较高的计算复杂度。与此同时，一类基于原子范数最小化及Toeplitz矩阵范德蒙德分解的无网格方法也被提出[16-18]，但是这类方法仅适用于均匀阵列。对于非均匀阵列，Zhou等人[19,20]提出了基于阵元内插的Toeplitz矩阵重构方法，并在互质阵列上取得了良好的效果。然而阵元内插不可避免地带来额外的估计误差，并且半定规划问题求解具有较高的计算复杂度。
针对上述算法存在的问题，本文将离网格的思想引入到IAA算法中，并对IAA算法功率计算进行修正，提出了一种基于修正IAA功率谱的离网格DOA估计算法(Off-Grid Iterative Adaptive Approach, OGIAA)。该算法可以解决信源位置与网格不匹配等问题，并且能够进行全局寻优以实现高精度的DOA估计。算法可以分为基于修正IAA算法功率谱的粗估计和基于最小平方误差准则的偏移量求解两个部分。首先，对IAA方法求出的功率谱进行修正，得到预定义网格上更加准确的信号功率分量和噪声功率分量；之后，基于最小平方误差准则构建代价函数，利用泰勒二次展开并最小化代价函数得到初始偏移量；最后，交替优化功率分量和网格偏移量，直至满足收敛条件。仿真验证了算法的有效性。
2. 基于修正IAA功率谱算法的粗估计
本文分别在第2节和第3节推导了OGIAA算法的两个步骤。首先，通过修正IAA算法求出的空域功率谱得到信号功率和波达角方向的粗估计结果。假设存在一个M元均匀线阵，各个阵元全向同性且阵元间距为d，远场处有K个信号{{\boldsymbol{s}}_k}以角度{\theta _k}抵达线阵，则阵列接收到的窄带信号数据可以表示为
y(n) = \sum\limits_{k = 1}^K {{\boldsymbol{A}}({\theta _k}){{\boldsymbol{s}}_k}(n)} + {\boldsymbol{e}}(n),n = 1,2, \cdots ,N (1) 其中，N是快拍数，{\boldsymbol{A}}是大小为M×K的导向矢量矩阵， {\boldsymbol{A}} = ({\boldsymbol{a}}({\theta _1}),{\boldsymbol{a}}({\theta _2}), \cdots ,{\boldsymbol{a}}({\theta _K})) ，在远场条件下，导向矢量 {\boldsymbol{a}}({\theta _k}) = {{\text{e}}^{ - {\text{j}}2\pi md\sin {\theta _k}/\lambda }} ，则有限快拍下的信号协方差矩阵可以表示为
{\boldsymbol{R}} = \frac{1}{{\boldsymbol{N}}}{\boldsymbol{y}}{{\boldsymbol{y}}^{\text{H}}} = {\boldsymbol{AP}}{{\boldsymbol{A}}^{\text{H}}} (2) 其中，{\boldsymbol{P}} = {\rm{diag}}({\boldsymbol{p}})，{\boldsymbol{p}}表示K个信源的功率分量组成的向量。此外，除了期望信号{{\boldsymbol{s}}_k}之外的干扰和噪声的协方差矩阵{\boldsymbol{Q}}({\theta _k})可以表示为
{\boldsymbol{Q}}({\theta _k}) = {\boldsymbol{R}} - p({\theta _k}){\boldsymbol{a}}({\theta _k}){{\boldsymbol{a}}^{\text{H}}}({\theta _k}) (3) 接下来根据基于加权最小二乘法 (Weighted Least Squares, WLS)的代价函数 {J_{{\rm{WLS}}}} [21]得到波达角方向为 {\theta _k} 的信号分量{{\boldsymbol{s}}_k}
\begin{split} {J_{{\rm{WLS}}}} =& \sum\limits_{n = 1}^N {{({\boldsymbol{y}}(n) - {\boldsymbol{a}}^{\text{H}}({\theta _k}){{\boldsymbol{s}}_k}(n))}}{Q^{ - 1}}({\theta _k})\\ & \cdot({\boldsymbol{y}}(n) - {\boldsymbol{a}}({\theta _k}){{\boldsymbol{s}}_k}(n)) ,n = 1,2, \cdots ,N \end{split} (4) 最小化式(4)得到
{{\boldsymbol{s}}_k}(n) = \frac{{{{\boldsymbol{a}}^{\text{H}}}({\theta _k}){{\boldsymbol{Q}}^{ - 1}}{\boldsymbol{y}}(n)}}{{{{\boldsymbol{a}}^{\text{H}}}({\theta _k}){{\boldsymbol{Q}}^{ - 1}}{\boldsymbol{a}}({\theta _k})}},n = 1,2, \cdots ,N (5) 根据式(3)和矩阵求逆定理，式(5)可以进一步化简为
{{\boldsymbol{s}}_k}(n) = \frac{{{{\boldsymbol{a}}^{\text{H}}}({\theta _k}){{\boldsymbol{R}}^{ - 1}}{\boldsymbol{y}}(n)}}{{{{\boldsymbol{a}}^{\text{H}}}({\theta _k}){{\boldsymbol{R}}^{ - 1}}{\boldsymbol{a}}({\theta _k})}},n = 1,2, \cdots ,N (6) 要求出信号在空域上的功率谱，首先基于等角度划分的原则在空间域上设置过完备表示的离散网格\varPhi = ({\phi _1},{\phi _2}, \cdots ,{\phi _Q})，其中Q \gg M \gt K，网格角度对应的导向矢量矩阵为{{\bar {\boldsymbol{A}}}}(\varPhi ) = ({\boldsymbol{a}}({\phi _1}), {\boldsymbol{a}}({\phi _2}), \cdots , {\boldsymbol{a}}({\phi _Q}))，根据式(1)的信号模型，对每个网格点对应的功率分量进行初始估计
\begin{split} {{{\bar {\boldsymbol{p}}}}^{(1)}}({\phi _q}) &= \frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {{{{{\bar {\boldsymbol{s}}}}}^{(1)}}({\phi _q},n)} \right|}^2} } \\ & =\frac{1}{{{{\boldsymbol{a}}^{\text{H}}}({\phi _q}){\boldsymbol{a}}({\phi _q})N}}\sum\limits_{n = 1}^N {{{\left| {{{\boldsymbol{a}}^{\text{H}}}({\phi _q}){\boldsymbol{y}}(n)} \right|}^2}} \end{split} (7) 其中，{\boldsymbol{\bar s}}({\phi _q},n), {\boldsymbol{\bar p}}({\phi _q})分别是字典角度{\phi _q}对应的信号分量和功率分量，根据式(6)进一步更新网格上的功率谱，在第i次迭代有
{{{\bar {\boldsymbol{R}}}}^{(i)}} = {{\bar {\boldsymbol{A}}}}(\varPhi ){{{\bar {\boldsymbol{P}}}}^{(i)}}(\varPhi ){{\bar {\boldsymbol{A}}}}(\varPhi ) (8) {{\boldsymbol{\bar s}}^{(i + 1)}}({\phi _q},n) = \frac{{{{\boldsymbol{a}}^{\text{H}}}({\phi _q}){{{\boldsymbol{\bar R}}}^{ - 1(i)}}{\boldsymbol{y}}(n)}}{{{{\boldsymbol{a}}^{\text{H}}}({\phi _q}){{{\boldsymbol{\bar R}}}^{ - 1(i)}}{\boldsymbol{a}}({\phi _q})}},n = 1,2, \cdots ,N (9) {{\boldsymbol{\bar p}}^{(i + 1)}}({\phi _q}) = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {{{{\boldsymbol{\bar s}}}^{(i + 1)}}({\phi _q},n)} \right|}^2}} (10) 其中，{\boldsymbol{\bar P}}(\varPhi ) = {\rm{diag}}({\boldsymbol{\bar p}})，循环至满足收敛条件\left\| {{{{\boldsymbol{\bar p}}}^{(i + 1)}}(\varPhi ) - {{{\boldsymbol{\bar p}}}^{(i)}}(\varPhi )} \right\|_2^2 \lt \varepsilon，得到信号在预置网格上的功率谱。
如果信源数已知，则可以直接根据功率谱得到对应的功率谱峰值分量{\bar p_k}和对应的粗估计结果 {\bar \theta _k} 。如果信源数未知，则可以根据贝叶斯信息准则(Bayesian Information Criterion, BIC)[22]进行粗估计。
\begin{split} & {\text{BIC}}(\eta )\\ & \quad{\text{ = }}2MN\ln \left( {\sum\limits_{n = 1}^N {\left\| {{\boldsymbol{y}}(n) - \sum\limits_{k \in \{ J \cup j\} } {{\boldsymbol{a}}({\phi _k}){\boldsymbol{\hat s}}({\phi _k},n)} } \right\|} _2^2} \right) \\ & \qquad + \eta \ln (2MN) \\[-10pt] \end{split} (11) 其中，\eta 是剩余的峰值数，j是功率谱峰值对应的网格位置，J是选中网格的集合。
假设附加噪声e(n)为高斯白噪声，文献[7]直接利用 M \cdot \min ({\boldsymbol{\bar p}}({\bar \theta _k})) 求解噪声功率，但是这一表达式得到的噪声功率估计结果并不准确。本文利用IAA求解过程中得到的信号分量估计出噪声分量
\bar e(n) = y(n) - \sum\limits_{k = 1}^K {A({{\bar \theta }_k})\bar s({{\bar \theta }_k},n)} (12) 求出噪声分量{\boldsymbol{\bar e}}(n)的方差，就能得到估计更为准确的噪声功率 \bar \sigma _n^2 ，此时进一步对功率谱修正，得到修正后的峰值处功率分量{\hat p_k}
{\hat p_k} = {\bar p_k} - \frac{{\bar \sigma _n^2}}{M} (13) 3. 基于最小平方误差准则的偏移量求解
接下来求解网格偏移量得到精细估计的结果。首先对协方差矩阵R进行向量化
{{\bar {\boldsymbol{y}}}} = {\text{vec}}({\boldsymbol{R}}) = {{\bar {\boldsymbol{A}}}}(\theta ){{\bar {\boldsymbol{p}}}} + {\boldsymbol{\bar i}}\sigma _n^2 (14) 其中，{{\bar {\boldsymbol{A}}}}(\theta ) = {\boldsymbol{A}}(\theta ) \odot {{\boldsymbol{A}}^ * }(\theta )， \odot 表示克罗内克积，{\boldsymbol{\bar i}}是M阶的单位阵I向量化后的单位向量。
根据 {\boldsymbol{\bar y}} 的表达式，结合粗估计结果，基于最小平方误差准则设置目标函数F
F({\bar \theta _k}) = \left\| {{\boldsymbol{\bar y}} - {\boldsymbol{\bar i}}\sigma _n^2 - \sum\limits_{k = 1}^K {{{\bar {\boldsymbol{A}}}}({{\bar \theta }_k}){{\hat p}_k}} } \right\|_2^2 = {{\boldsymbol{z}}^{\text{H}}}({\bar \theta _k}){\boldsymbol{z}}({\bar \theta _k}) (15) 其中，{\boldsymbol{z}}({\bar \theta _k}) = {\boldsymbol{\bar y}} - {{\bar {\boldsymbol{i}}}}\sigma _n^2 - \displaystyle\sum\nolimits_{k = 1}^K {{{\bar {\boldsymbol{A}}}}({{\bar \theta }_k}){{{{\hat {\boldsymbol{p}}}}}_k}}，接下来分别求解目标函数F对 {\bar \theta _k} 的1阶导数和2阶导数
F'({\bar \theta _k}) = 2{\text{real}}\left({\left( - \sum\limits_{k = 1}^K {{{\bar {\boldsymbol{A}}'}}({{\bar \theta }_k}){{\hat p}_k}} \right)^{\text{H}}}{\boldsymbol{z}}\right) (16) \begin{split} F''({\bar \theta _k}) =& 2{\text{real}}({( - \sum\limits_{k = 1}^K {{{\bar {\boldsymbol{A}}''}}({{\bar \theta }_k}){{\hat p}_k}} )^{\text{H}}}{\boldsymbol{z}}) \\ & + 2{\text{real}}\left({\left( - \sum\limits_{k = 1}^K {{{\bar {\boldsymbol{A}}'}}({{\bar \theta }_k}){{\stackrel \frown{p} }_k}} \right)^{\text{H}}}\right.\\ & \left.\cdot\left( - \sum\limits_{k = 1}^K {{{\bar {\boldsymbol{A}}'}}({{\bar \theta }_k}){{\stackrel \frown{p} }_k}} \right)\right) \end{split} (17) 其中，{\text{real}}( \cdot )表示取括号内复数变量的实部，在目标函数F中对第k个信源的粗估计结果 {\bar \theta _k} 进行2阶泰勒展开，得到新的代价函数 \bar F
\bar F = F({\bar \theta _k}) + F'({\bar \theta _k}){\delta _k} + \frac{1}{2}F''({\bar \theta _k})\delta _k^2 (18) 其中， {\delta _k} 是 {\hat \theta _k} 的偏移量，为了求出代价函数 \bar F 的最小值，将 \bar F 对偏移量{\delta _k}求导，并令导数为零，解得
\delta _k^{(1)} = - F'({\bar \theta _k})/F''({\bar \theta _k}) (19) 求解K次得到K个偏移量，则第1次DOA估计的结果为
\hat \theta _k^{(1)} = {\bar \theta _k} + \delta _k^{(1)} (20) 将第1次估计的结果代回IAA算法中，重复式(7)—式(10)，求出新的信号功率分量和噪声功率分量，再代入式(15)—式(19)中求出新的偏移量。交替优化功率和偏移量，假设循环L次后满足收敛条件\delta _k^{(L)} - \delta _k^{(L - 1)} \le \beta，结束循环。最终估计结果为
\hat \theta _k^{(L)} = {\bar \theta _k} + \delta _k^{(1)} + \cdots + \delta _k^{(L)} (21) 综上所述，算法具体的步骤如下：
步骤1 根据式(7)—式(10)的IAA算法得到参数粗估计的结果{\bar \theta _k}，{\bar p_k}， \bar \sigma _n^2 ，并且根据式(13)对功率谱进行修正，得到修正后的信号功率{\hat p_k}。
步骤2 基于最小平方误差准则，根据粗估计的结果设置代价函数{\bar F^{(1)}}，按式(15)—式(19)最小化{\bar F^{(1)}}得到偏移量\delta _k^{(1)}，根据式(20)能得到精细估计结果\hat \theta _k^{(1)}。
步骤3 将步骤2的估计结果代回IAA算法中，更新功率谱并修正，得到\hat p_k^{(1)}, \bar \sigma _n^{2(1)} 。
步骤4 利用更新后的参数重新构建目标函数{\bar F^{(2)}}，最小化{\bar F^{(2)}}得到新的偏移量\delta _k^{(2)}。
步骤5 重复步骤3、步骤4，交替优化功率分量和偏移量，当满足\delta _k^{(L)} - \delta _k^{(L - 1)} \le \beta或达到最大迭代次数{i_{\max }}时结束循环，得到最终的估计结果\hat \theta _k^{(L)} = {\bar \theta _k} + \delta _k^{(1)} + \cdots + \delta _k^{(L)}。
4. 仿真验证
本节首先研究OGIAA算法中的一些预定义参数，如字典间隔、最大迭代次数的取值对估计结果的影响。之后分别在均匀阵与互质阵上进行仿真实验，通过对比SOMP[10], OGSBI[11]和IPOC[14]等算法，验证本文提出的OGIAA算法的有效性。
仿真1 为了探究最大迭代次数和字典网格间隔对算法估计结果的影响，设置阵元数M=10，快拍数N=100，待估计信源个数K=5，波达角方向分别为40.80°, 17.78°, 5.25°, –28.28°, –51.30°，假设估计结果\left| {{{\hat \theta }_i} - {\theta _i}} \right| \le {0.15^ \circ }为估计正确，在每个条件下进行T=200次蒙特卡罗实验。不同迭代次数imax和不同网格间隔r在信噪比–10～30 dB下的估计正确率分别如图1(a)、图1(b)所示。
由图1可以看到，图1(a)中除了1次迭代的条件下精度明显降低，在两次迭代后几乎都能达到最高精度，可见本文所提算法具有较快的收敛速度。图1(b)中除了网格间隔为4°时在低信噪比情况下估计精度略有降低，其余网格间隔下的估计精度几乎一致，可以看出预定义字典间隔的设置对所提算法估计精度影响有限。综上所述，在计算量受限的场合，减少最大迭代次数或者增大网格间隔都是一种减少算法运算量的有效选择。
仿真2 假设存在阵元数M=10的均匀阵列，待估计信源个数K=2，信源波达角分别为{\theta _1}=40.8°, {\theta _2}=–51.3°，信噪比SNR=10 dB，快拍数N=100，设置字典离散网格间隔为r=2°，图2为本文所提OGIAA算法与IAA, SOMP, OGSBI和IPOC算法的空域谱对比结果。
由图2放大的部分可以看到，由于待估计信源角度不会正好定位在网格上，所以IAA算法峰值对应的网格无法正确估计出信源角度，而其余4种离网格估计方法都能得到准确的估计结果。为了进一步说明本文所提算法的有效性，将算法估计精度用均方根误差(Root Mean Squared Error, RMSE)表示
{\rm{RMSE}}{\text{ = }}\sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^T {\displaystyle\sum\limits_{k = 1}^K {[{{({{\hat \theta }_{ik}} - {\theta _k})}^2}]} } }}{{TK}}} (22) 保持其他条件不变，在–10～30 dB的范围内改变信噪比的取值，并令快拍数N分别为200和20，在每个条件下进行T=200次蒙特卡罗实验，则不同算法的估计精度为随信噪比的变化如图3所示。
由图3(a)可以看到，当N=200时，由于网格不匹配的原因，IAA算法估计精度最低，而OGSBI算法和SOMP算法无法做到全局寻优，导致精度受限。IPOC算法对均匀阵列的虚拟阵进行处理，虽然减少了计算量，但是估计精度受到限制。MUSIC算法虽然在高信噪比下具有较高的估计精度，然而在低信噪比下精度不足。相比之下，本文提出的OGIAA算法精度最高，并且能接近克拉默-拉奥界(Cramer-Rao Bound, CRB)。由图3(b)可以看到，当N=20时，OGSBI算法和MUSIC算法在高信噪比下能取得较好的效果，但是在低信噪比下精度就无法保证，而本文所提算法在不同信噪比和快拍数下都具有更高的估计精度，并且在高信噪比下估计精度能接近CRB。
仿真3 互质阵列由两个阵元数互质的子阵组成，利用2阶相关矩阵向量化，并删去其中重复的元素，观察剩余数据的结构，其对应的虚拟阵列具有更大的阵列口径和高达 O({M_1}{M_2}) 的阵列自由度，因此在近几年，基于互质阵列扩展虚拟阵列的信号处理技术得到了广大学者的关注。为了说明本文算法应用在高自由度的稀疏阵上仍然具有较高的估计精度，如图4所示，假设存在一个{M_1} = 3, {M_2} = 5的互质阵列，总阵元个数M = 7，利用2阶相关矩阵向量化，可以得到阵元数\bar M = 21的中间连续，两端稀疏的扩展虚拟阵列。
对虚拟阵列等效单快拍接收数据 {\boldsymbol{\tilde y}} 进行处理，此时更改代价函数F的表达式为
{{\tilde {\boldsymbol{y}}}} = {{{\boldsymbol{G}}\bar {\boldsymbol{y}}}} = {{\tilde {\boldsymbol{Ap}}}} + {{\bar {\boldsymbol{i}}}}\sigma _n^2 (23) F = \left\| {{{\tilde {\boldsymbol{y}}}} - {{\tilde {\boldsymbol{i}}}}\sigma _n^2 - \sum\limits_{k = 1}^K {{{\tilde {\boldsymbol{A}}}}({{\bar \theta }_k}){{\hat p}_k}} } \right\|_2^2 = {{{\tilde {\boldsymbol{z}}}}^{\text{H}}}{{\tilde {\boldsymbol{z}}}} (24) 其中，{{\tilde {\boldsymbol{z}}}} = {{\tilde {\boldsymbol{y}}}} - {{\tilde {\boldsymbol{i}}}}\sigma _n^2 - \displaystyle\sum\nolimits_{k = 1}^K {{{\tilde {\boldsymbol{A}}}}({{\bar \theta }_k}){{\hat p}_k}}，G是大小为\bar M \times {M^2}的选择矩阵，每行只有一个单元为1，其余单元都为0，目的是剔除{{\tilde {\boldsymbol{y}}}}中的重复元素，构建虚拟阵列的单快拍接收数据。{{\tilde {\boldsymbol{A}}}}是非均匀虚拟阵对应的导向矢量矩阵，{{\tilde {\boldsymbol{i}}}}是除了中间单元为1其余单元都为0的列向量。
设置信噪比SNR=20 dB，快拍数N=200，待估计信源个数K=9，其波达角方向在{\theta _1}=–60.3°，{\theta _2}=60.8°间均匀分布。图5为利用虚拟阵列单快拍数据进行DOA估计的结果。可以看到，对于总阵元数为7的互质阵来说，利用本文算法对其虚拟阵列的单快拍接收数据进行DOA估计，可以准确估计出比阵元数更多的信源个数。
为了进一步说明本文算法在互质阵DOA估计上的优势，假设待估计信源波达角为40.8°, –51.3°，保持其他条件不变，分别改变信噪比和快拍数的取值，每个条件下进行T=200次蒙特卡罗实验，不同算法估计精度随信噪比和快拍数的变化如图6所示。由图6(a)可以看到，当N=200时，对于虚拟阵列等效单快拍接数据，SOMP和OGSBI算法无法做到全局寻优，而IPOC算法和OGIAA算法具有更高的估计精度。MUSIC算法由于只能对虚拟阵列中间连续阵元进行平滑处理，导致两端稀疏部分阵元的接收数据丢失，因此算法精度受限。由图6(b)可以看到，当N=20时，IPOC算法在低信噪比情况下精度无法保证。相比之下，OGIAA算法仍然具有较高的估计精度。综上所述，在不同信噪比和快拍数下，本文所提OGIAA算法能做到全局寻优，具有更强的估计性能。
5. 结论
本文提出了一种基于修正IAA算法功率谱的离网格DOA估计方法，有效解决了常规稀疏重构算法字典网格与信源位置不匹配问题，实现了高精度的离网格DOA估计。本文算法以修正IAA算法得到的功率谱构建基于最小平方误差准则的代价函数，并通过泰勒展开最小化代价函数求解偏移量，原理清晰，结构简单，无正则化系数的干扰。仿真结果表明，相比其他离网格DOA估计方法，本文算法具有更高的估计精度，能准确估计出偏离网格的信源波达角方向。
-
[1] 金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2): 470–475. doi: 10.3724/SP.J.1146.2009.00497JIN Jian, GU Yuantao, and MEI Shunliang. An introduction to compressive sampling and its applications[J]. Journal of Electronics &Information Technology, 2010, 32(2): 470–475. doi: 10.3724/SP.J.1146.2009.00497 [2] YANG Zai, LI Jian, STOICA P, et al. Chapter 11 - sparse methods for direction-of-arrival estimation[M]. CHELLAPPA R and THEODORIDIS S. Academic Press Library in Signal Processing, Volume 7. Academic Press, 2018: 509–581. [3] TIBSHIRANI R. Regression shrinkage and selection via the lasso: A retrospective[J]. Journal of the Royal Statistical Society:Series B, 2011, 73(3): 273–282. doi: 10.1111/j.1467-9868.2011.00771.x [4] LI Lixiang, FANG Yuan, LIU Liwei, et al. Overview of compressed sensing: Sensing model, reconstruction algorithm, and its applications[J]. Applied Sciences, 2020, 10(17): 5909. doi: 10.3390/app10175909 [5] ZHANG Yongchao, LI Jie, LI Minghui, et al. Online sparse reconstruction for scanning radar using beam-updating q-SPICE[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 19: 3503905. doi: 10.1109/LGRS.2021.3058404 [6] 何团, 唐波, 张玉. 基于加权SPICE的MIMO-STAP稀疏恢复算法[J]. 信号处理, 2019, 35(8): 1417–1424. doi: 10.16798/j.issn.1003-0530.2019.08.017HE Tuan, TANG Bo, and ZHANG Yu. Sparse recovery algorithm of MIMO-STAP based on weighted SPICE[J]. Journal of Signal Processing, 2019, 35(8): 1417–1424. doi: 10.16798/j.issn.1003-0530.2019.08.017 [7] WANG Hao, ZHANG Hong, and MA Qiming. Sparse spectrum fitting algorithm using signal covariance matrix reconstruction and weighted sparse constraint[J]. Multidimensional Systems and Signal Processing, 2022, 33(3): 807–817. doi: 10.1007/s11045-021-00811-x [8] STOICA P and BABU P. Sparse estimation of spectral lines: Grid selection problems and their solutions[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 962–967. doi: 10.1109/TSP.2011.2175222 [9] 徐文先, 高志奇, 徐伟, 等. 基于迭代自适应的字典校正空时自适应处理算法[J]. 信号处理, 2021, 37(11): 2216–2226. doi: 10.16798/j.issn.1003-0530.2021.11.024XU Wenxian, GAO Zhiqi, XU Wei, et al. Space-time adaptive processing with dictionary calibration based on iterative adaptive approach[J]. Journal of Signal Processing, 2021, 37(11): 2216–2226. doi: 10.16798/j.issn.1003-0530.2021.11.024 [10] AUSTIN C D, ASH J N, and MOSES R L. Dynamic dictionary algorithms for model order and parameter estimation[J]. IEEE Transactions on Signal Processing, 2013, 61(20): 5117–5130. doi: 10.1109/TSP.2013.2276428 [11] GRETSISTAS A and PLUMBLEY M D. An alternating descent algorithm for the off-grid DOA estimation problem with sparsity constraints[C]. 2012 Proceedings of the 20th European Signal Processing Conference, Bucharest, Romania, 2012: 874–878. [12] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378 [13] WU Xiaohuan, ZHU Weiping, and YAN Jun. Direction of arrival estimation for off-grid signals based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2016, 16(7): 2004–2016. doi: 10.1109/JSEN.2015.2508059 [14] MA Yanan, CAO Xianbin, and WANG Xiangrong. Multi-source off-grid DOA estimation using iterative phase offset correction in coarray domain[J]. Digital Signal Processing, 2021, 112: 102998. doi: 10.1016/j.dsp.2021.102998 [15] 王洪雁, 于若男, 潘勉, 等. 基于协方差矩阵重构的离网格DOA估计方法[J]. 电子与信息学报, 2021, 43(10): 2863–2870. doi: 10.11999/JEIT200697WANG Hongyan, YU Ruonan, PAN Mian, et al. Off-grid DOA estimation method based on covariance matrix reconstruction[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2863–2870. doi: 10.11999/JEIT200697 [16] YANG Zai and XIE Lihua. Enhancing sparsity and resolution via reweighted atomic norm minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 995–1006. doi: 10.1109/TSP.2015.2493987 [17] CHUNG H, JOO J M, and KIM S Y. Off-grid DOA estimation on non-uniform linear array using constrained hermitian matrix[J]. Energies, 2020, 13(21): 5775. doi: 10.3390/en13215775 [18] 陈涛, 史林, 黄桂根, 等. 适用于任意几何结构平面阵列的无网格DOA估计算法[J]. 电子与信息学报, 2022, 44(3): 1052–1058. doi: 10.11999/JEIT210038CHEN Tao, SHI Lin, HUANG Guigen, et al. Gridless DOA estimation algorithm for planar arrays with arbitrary geometry[J]. Journal of Electronics &Information Technology, 2022, 44(3): 1052–1058. doi: 10.11999/JEIT210038 [19] ZHOU Chengwei, GU Yujie, SHI Zhiguo, et al. Off-grid direction-of-arrival estimation using coprime array interpolation[J]. IEEE Signal Processing Letters, 2018, 25(11): 1710–1714. doi: 10.1109/LSP.2018.2872400 [20] ZHANG Xue, ZHENG Zhi, WANG Wenqin, et al. DOA estimation of coherent sources using coprime array via atomic norm minimization[J]. IEEE Signal Processing Letters, 2022, 29: 1312–1316. doi: 10.1109/LSP.2022.3179336 [21] LI Jian and STOICA P. An adaptive filtering approach to spectral estimation and SAR imaging[J]. IEEE Transactions on Signal Processing, 1996, 44(6): 1469–1484. doi: 10.1109/78.506612 [22] YARDIBI T, LI Jian, and STOICA P. Nonparametric and sparse signal representations in array processing via iterative adaptive approaches[C]. The 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2008: 278–282. 期刊类型引用(4)
1. 刘帅，许媛媛，闫锋刚，金铭. 泰勒展开与交替投影最大似然结合的离网格DOA估计算法. 电子与信息学报. 2024(08): 3219-3227 . 
本站查看2. 于丹阳，杜磊. 一种基于快速迭代自适应算法的毫米波雷达波达角高精度测量方法. 计量科学与技术. 2024(11): 3-9+21 . 
百度学术3. 裴秋秋，何琳，帅长庚，胡鹏涛，孙玉臣. 基于改进迭代自适应算法的水下近场噪声源定位. 海军工程大学学报. 2024(06): 66-70 . 百度学术4. 张伟，杨继承，贾沛源，闫紫航. 基于轻量MIMO毫米波雷达的高精度检测与定位. 公路交通科技. 2023(S1): 446-455 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
计量
- 文章访问数: 1318
- HTML全文浏览量: 739
- PDF下载量: 225
- 被引次数: 9
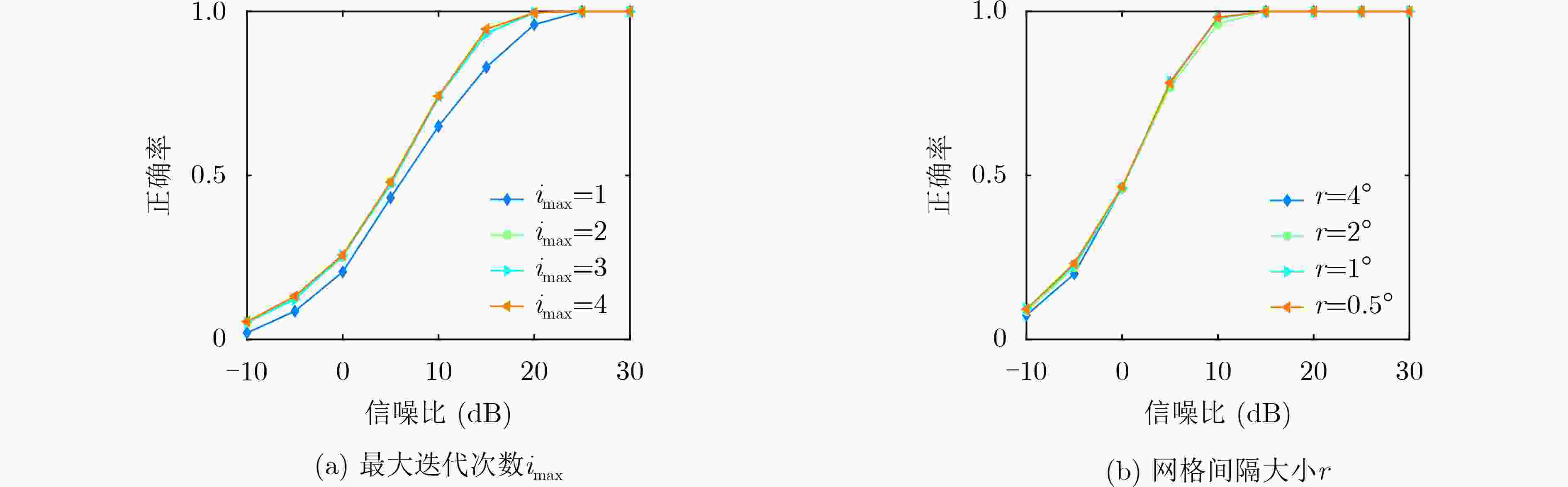
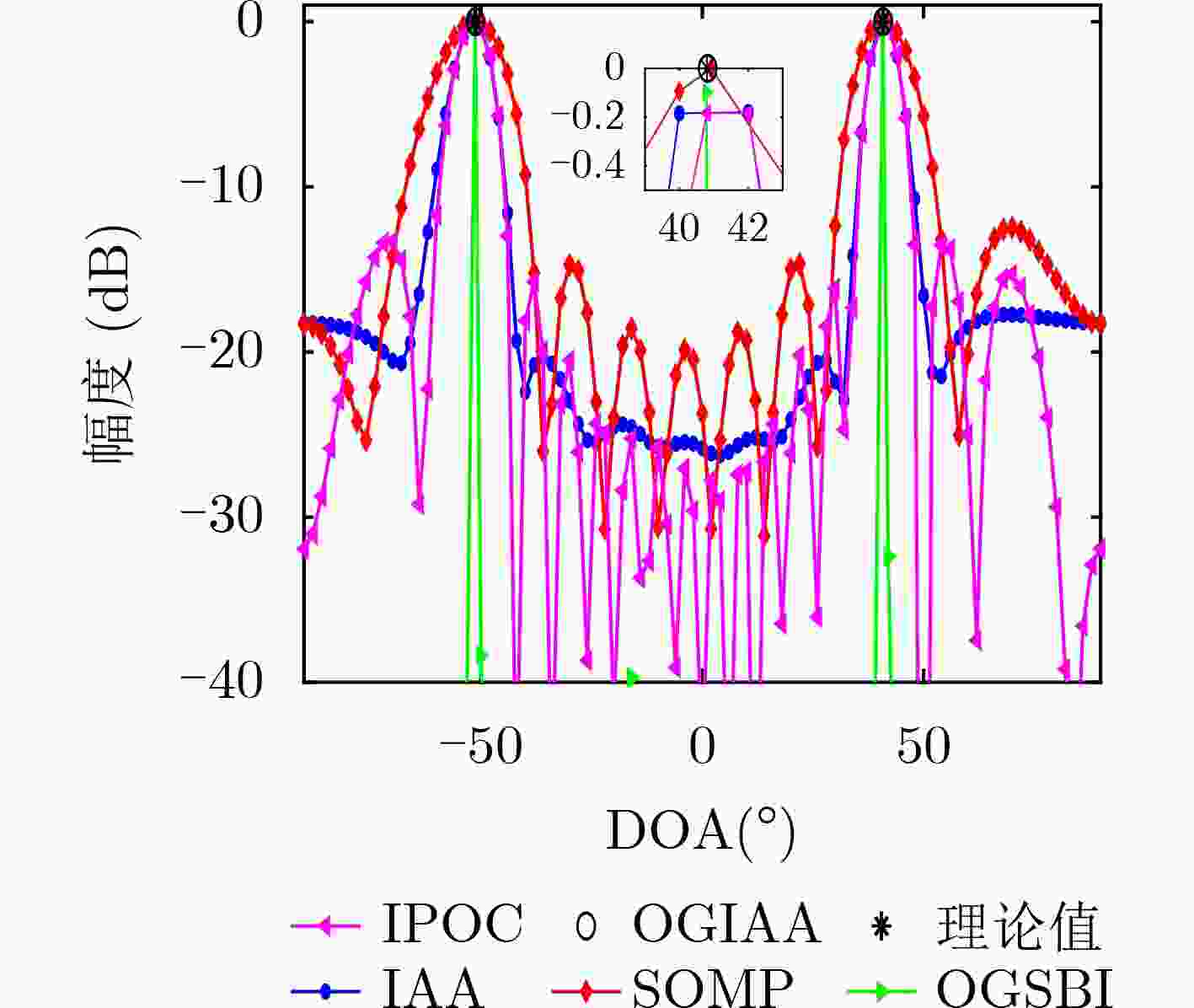
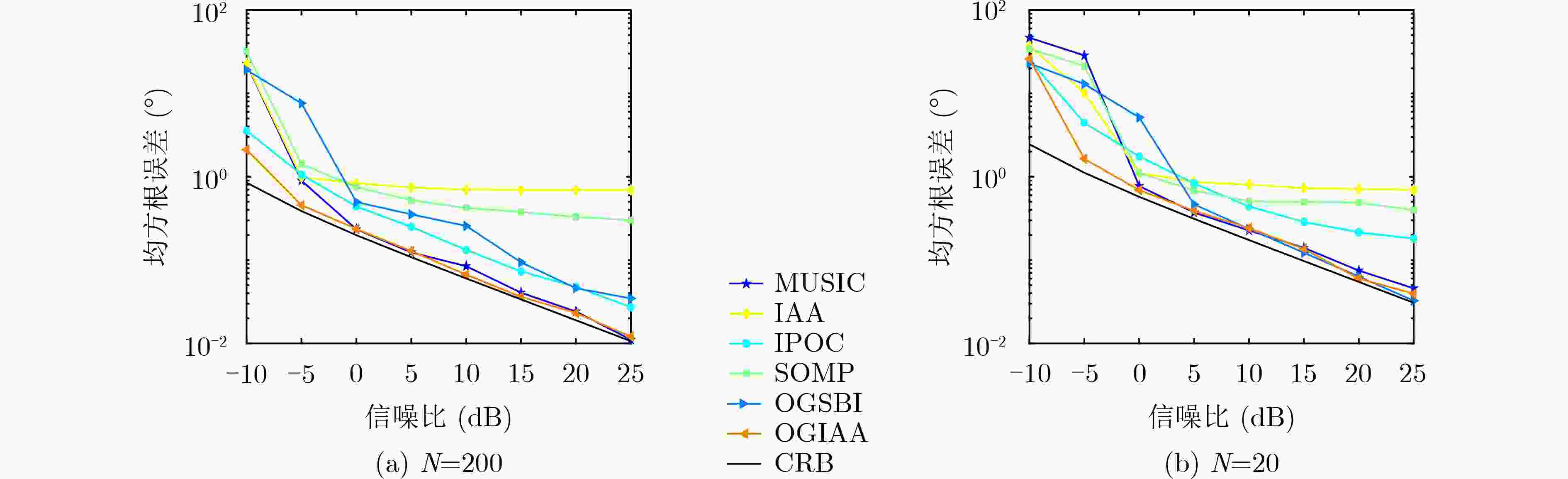
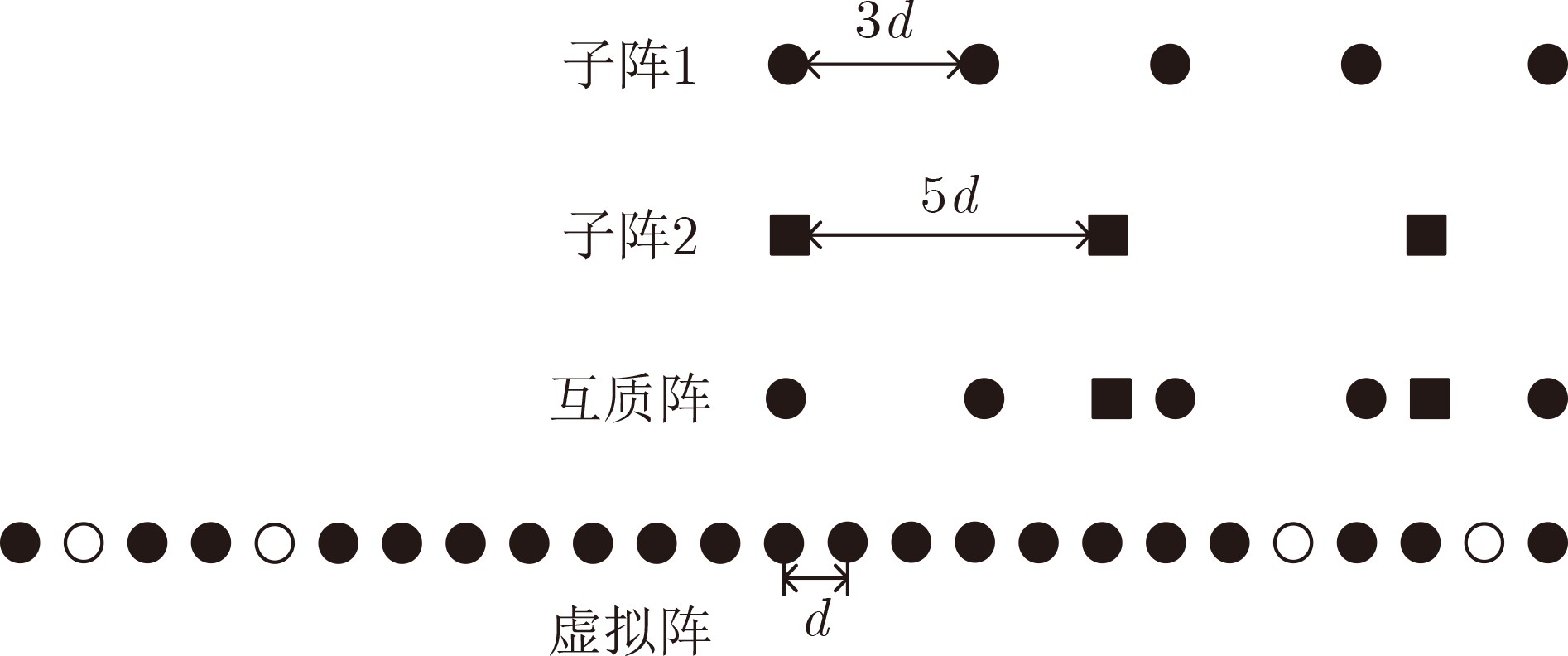
下载:
