Mean Estimation Mechanisms under (ε, δ)-Local Differential Privacy
-
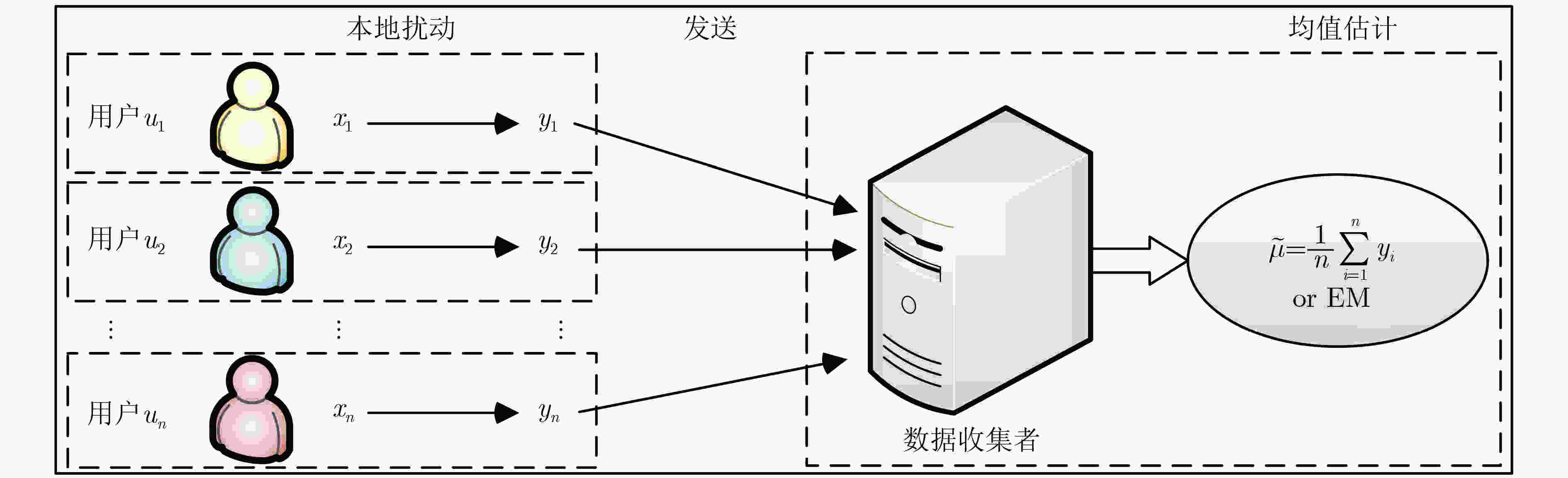
摘要: 相对于ε-本地差分隐私(LDP)机制,(ε, δ)-本地差分隐私模型下的方案具有更小的误差边界和更高的数据效用。然而,当前的(ε, δ)-本地差分隐私均值估计机制仍存在估计误差大、数据效用低等问题。因此,针对均值估计问题,该文提出两种新的(ε, δ)-本地差分隐私均值估计机制:基于区间的均值估计机制(IM)和基于近邻的均值估计机制(NM)。IM的主要思想是:划分扰动后的数据到3个区间,真实数据以较大概率扰动到中间的区间,以较小概率扰动到两边的区间,收集者直接对扰动数据求均值得到无偏估计。NM的主要思想是:把真实数据以较大概率扰动到其邻域,以较小概率扰动到距离较远的值,收集者结合期望最大化算法得到高准确度的估计均值。最后,该文通过理论分析证明了IM和NM均可以满足隐私保护要求,并通过实验证实了IM和NM的数据效用优于现有机制。Abstract: Compared with the ε-Local Differential Privacy (LDP) mechanism, the scheme under (ε, δ)-local differential privacy has a smaller error bound and higher data utility. However, the current mean estimation mechanisms under (ε, δ)-local differential privacy still have problems such as large estimation error and low data utility. Therefore, for the mean estimation problem, two new mean estimation mechanisms under (ε, δ)-local differential privacy are proposed: the Interval-based Mechanism for mean estimation (IM) and the Neighbor-based Mechanism for mean estimation (NM). IM divides the perturbed data into three intervals. Then the real data is perturbed to the middle interval with a large probability, and the two sides are perturbed with a small probability. Collector averages directly the perturbed data to get an unbiased estimation. NM perturbs the real data to its near neighborhood with a large probability and perturbs it far away with a small probability. Then the collector applies the expectation maximization algorithm to obtain an estimated mean value with high accuracy. Finally, both IM and NM satisfy the privacy protection requirements are proved through theoretical analysis, and the data utility of IM and NM is superior to existing mechanisms is confirmed by experiments.
-
Key words:
- Privacy protection /
- Local Differential Privacy (LDP) /
- Data collection /
- Mean estimation
-
表 1 现有的满足(ε, δ)-LDP的均值估计机制的误差
GM[10] Opt-GM[11] NDM[12] MSE $\dfrac{2}{\varepsilon }\sqrt {2\ln \dfrac{ {1.25} }{\delta } }$ $ \dfrac{{\sqrt 2 }}{\varepsilon }(\xi + \sqrt {{\xi ^2} + \varepsilon } ) $* ${\left( {\dfrac{ { {{\rm{e}}^\varepsilon } + 1} }{ { {{\rm{e}}^\varepsilon } + 2\delta - 1} } } \right)^2}$ *:其中$ \xi $由${\rm{erfc} }(\xi ) - {{\rm{e}}^\varepsilon }{\rm{erfc} }(\sqrt { {\xi ^2} + \varepsilon } ) = 2\delta$计算可得,${\rm{erfc}}( \cdot )$是互补误差函数[13] 算法1 基于区间的均值估计机制(IM) 输入:用户${u_i}$的数据${x_i} \in [ - 1,1]$,隐私预算$\varepsilon $,松弛因子$\delta $ 输出:扰动数据${y_i} \in [ - C,C]$ (1) 初始时,令$q = \dfrac{ { {{\rm{e}}^{\varepsilon/2} } - 1 - 4\delta } }{ {2{{\rm{e}}^{\varepsilon/2} }({{\rm{e}}^{\varepsilon/2} } + 1 + 4\delta )} }$, $p = {{\rm{e}}^\varepsilon }q + \delta$, $a = \dfrac{1}{{4q}} - \sqrt {\dfrac{p}{{2q(q - p)}} + \dfrac{1}{{16{q^2}}}} $, $C = \dfrac{{1 - 2a(q - p)}}{{2p}}$, $b = a - C$,
$l({x_i}) = a{x_i} + b$, $r({x_i}) = a{x_i} - b$;(2) 对数据${x_i}$做如下扰动 ${\rm{pdf} }[{y_i} = t\left| { {x_i} } \right.] = \left\{ \begin{aligned} & p,\;{\text{ } }t \in \left[ {l({x_i}),r({x_i})} \right] \\ & q,\;{\text{ } }t \in \left[ {\left. { - C,l({x_i})} \right) \cup \left( {r({x_i}),C} \right.} \right] \end{aligned} \right.$ (2) (3) 将扰动后的$ {y_i} $发送给数据收集者。 算法2 基于近邻的均值估计机制(NM) 输入:用户${u_i}$的数据${x_i} \in [ - 1,1]$,隐私预算$\varepsilon $,松弛因子$\delta $ 输出:扰动数据${y_i} \in [ - b,b + 1]$ (1) 初始时,令$q = \dfrac{ {1 - 2b\delta } }{ {1 + 2b{{\rm{e}}^\varepsilon } } }$, $p = \dfrac{ { {{\rm{e}}^\varepsilon } + \delta } }{ {1 + 2b{{\rm{e}}^\varepsilon } } }$, $b = \dfrac{ { {{\rm{e}}^\varepsilon } - 1 - \varepsilon ({{\rm{e}}^\varepsilon } + \delta )} }{ {2({{\rm{e}}^\varepsilon }(1 - {{\rm{e}}^\varepsilon }) + \varepsilon ({{\rm{e}}^\varepsilon } + \delta ))} }$; (2) 格式化数据$ {x'_i} = {{({x_i} + 1)} \mathord{\left/ {\vphantom {{({x_i} + 1)} 2}} \right. } 2} $; (3) 对数据${x_i}$做如式(4)的扰动 ${\rm{pdf} }\left( { {y_i}\left| { { x'_i} } \right.} \right) = \left\{ \begin{gathered} p,{\text{ } }\left| { { x'_i} - {y_i} } \right| \le b \\ q,{\text{ } }\left| { { x'_i} - {y_i} } \right| > b \\ \end{gathered} \right.$ (4) (4) 将扰动后的$ {y_i} $发送给数据收集者。 算法3 NM机制的后处理过程 输入:扰动数据$ y = \{ {y_1},{y_2}, \cdots ,{y_n}\} $ 输出:估计均值$\tilde \mu $ (1) ${d_x} = {d_y} = {2^{\left\lfloor {{{\log }_2}\sqrt n } \right\rfloor }}$, $c = 0$; (2) 对NM的格式化输入区间$[0,1]$分组为$ {G^x} = \{ G_1^x,G_2^x, \cdots ,G_{{d_x}}^x\} $,输出区间$[ - b,b + 1]$分组为${G^y} = \{ G_1^y,G_2^y, \cdots ,G_{{d_y}}^y\} $; (3) 初始化原始数据在组$G_i^x$中的估计概率为$ {\tilde f^0} = \left\{ {{{\tilde f}^0}_1,{{\tilde f}^0}_2, \cdots ,{{\tilde f}^0}_{{d_x}}} \right\} = \left\{ {{1 \mathord{\left/ {\vphantom {1 {{d_x}}}} \right. } {{d_x}}},{1 \mathord{\left/ {\vphantom {1 {{d_x}}}} \right. } {{d_x}}}, \cdots ,{1 \mathord{\left/ {\vphantom {1 {{d_x}}}} \right. } {{d_x}}}} \right\} $; (4) 构建扰动矩阵${\boldsymbol{M}}$:${M_{ji} } = {\Pr _{{\rm{NM}}} }[G_j^y\left| {G_i^x} \right.]{\text{ } }(1 \le i \le {d_x},1 \le j \le {d_y})$; (5) while $c < 10000$ and $\left| {L({{\tilde f}^c}) - L({{\tilde f}^{c - 1}})} \right| > {10^{ - 3}}$: $c = c + 1$;
E步骤:$ {P_i} = {\tilde f_i}^{c - 1}\displaystyle\sum\nolimits_{j = 1}^{{d_y}} {{n_j}\dfrac{{\Pr [y \in G_j^y\left| {x \in G_i^x,{{\tilde f}^{c - 1}}} \right.]}}{{\Pr [y \in G_j^y\left| {{{\tilde f}^{c - 1}}} \right.]}}} = {\tilde f_i}^{c - 1}\displaystyle\sum\nolimits_{j = 1}^{{d_y}} {{n_j}\dfrac{{{M_{ji}}}}{{\displaystyle\sum\nolimits_{k = 1}^{{d_x}} {{M_{jk}}{{\tilde f}^{c - 1}}_k} }}} {\text{ }}(1 \le i \le {d_x}) $;M步骤:$ {\tilde f^c}_i = {{{P_i}} \mathord{\left/ {\vphantom {{{P_i}} {\displaystyle\sum\nolimits_{k = 1}^{{d_x}} {{P_k}} }}} \right. } {\displaystyle\sum\nolimits_{k = 1}^{{d_x}} {{P_k}} }}{\text{ }}(1 \le i \le {d_x}) $;
平滑步骤:${\tilde f^c}_i = \left\{ \begin{array}{lllllll} \dfrac{2}{3}{ {\tilde f}^c}_i + \dfrac{1}{3}{ {\tilde f}^c}_{i + 1}{\text{, } }& i = 1 \\ \dfrac{1}{2}{ {\tilde f}^c}_i + \dfrac{1}{4}({ {\tilde f}^c}_{i - 1} + { {\tilde f}^c}_{i + 1}){\text{, } }& 1 < i < {d_x} \\ \dfrac{1}{3}{ {\tilde f}^c}_{i - 1} + \dfrac{2}{2}{ {\tilde f}^c}_i{\text{, } }& i = {d_x} \\ \end{array} \right.$;end while (6) $\tilde \mu = \displaystyle\sum\nolimits_{i = 1}^{{d_x}} {{{\tilde f}^c}_i({{(1 + 2i)} \mathord{\left/ {\vphantom {{(1 + 2i)} {{d_x}}}} \right. } {{d_x}}} - 1)} $; (7) 返回$\tilde \mu $。 -
[1] HITAJ B, ATENIESE G, and PEREZ-CRUZ F. Deep models under the GAN: Information leakage from collaborative deep learning[C]. The ACM SIGSAC Conference on Computer and Communications Security, Dallas Texas, USA, 2017: 603–618. [2] 钱文君, 沈晴霓, 吴鹏飞, 等. 大数据计算环境下的隐私保护技术研究进展[J]. 计算机学报, 2022, 45(4): 669–701. doi: 10.11897/SP.J.1016.2022.00669QIAN Wenjun, SHEN Qingni, WU Pengfei, et al. Research progress on privacy-preserving techniques in big data computing environment[J]. Chinese Journal of Computers, 2022, 45(4): 669–701. doi: 10.11897/SP.J.1016.2022.00669 [3] KASIVISWANATHAN S P, LEE H K, NISSIM K, et al. What can we learn privately?[C]. The 49th Annual IEEE Symposium on Foundations of Computer Science, Philadelphia, USA, 2008: 531–540. [4] KASIVISWANATHAN S P, LEE H K, NISSIM K, et al. What can we learn privately?[J]. SIAM Journal on Computing, 2011, 40(3): 793–826. doi: 10.1137/090756090 [5] 冯登国, 张敏, 叶宇桐. 基于差分隐私模型的位置轨迹发布技术研究[J]. 电子与信息学报, 2020, 42(1): 74–88. doi: 10.11999/JEIT190632FENG Dengguo, ZHANG Min, and YE Yutong. Research on differentially private trajectory data publishing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 74–88. doi: 10.11999/JEIT190632 [6] XUE Qiao, ZHU Youwen, WANG Jian, et al. Locally differentially private distributed algorithms for set intersection and union[J]. Science China Information Sciences, 2021, 64: 219101. doi: 10.1007/s11432-018-9899-8 [7] WANG Ning, XIAO Xiaokui, YANG Yin, et al. Collecting and analyzing multidimensional data with local differential privacy[C]. 2019 IEEE 35th International Conference on Data Engineering, Macao, China, 2019: 638–649. [8] LI Zitao, WANG Tianhao, LOPUHAÄ-ZWAKENBERG M, et al. Estimating numerical distributions under local differential privacy[C]. The 2020 ACM SIGMOD International Conference on Management of Data, Portland, USA, 2020: 621–635. [9] BASSILY R. Linear queries estimation with local differential privacy[C]. The 22nd International Conference on Artificial Intelligence and Statistics, Naha, Japan, 2019: 721–729. [10] DWORK C and ROTH A. The algorithmic foundations of differential privacy[J]. Foundations and Trends® in Theoretical Computer Science, 2014, 9(3/4): 211–407. doi: 10.1561/0400000042 [11] BALLE B and WANG Yuxiang. Improving the Gaussian mechanism for differential privacy: Analytical calibration and optimal denoising[C]. The 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 403–412. [12] WANG Teng, ZHAO Jun, HU Zhi, et al. Local differential privacy for data collection and analysis[J]. Neurocomputing, 2021, 426: 114–133. doi: 10.1016/j.neucom.2020.09.073 [13] TELLAMBURA C and ANNAMALAI A. Efficient computation of erfc(x) for large arguments[J]. IEEE Transactions on Communications, 2000, 48(4): 529–532. doi: 10.1109/26.843116 [14] YEH I C and LIEN C H. The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients[J]. Expert Systems with Applications, 2009, 36(2): 2473–2480. doi: 10.1016/j.eswa.2007.12.020 [15] Minnesota Population Center. Integrated public use microdata series-international: version 7.3 [dataset][EB/OL]. https://doi.org/10.18128/D020.V7.3. -





 下载:
下载:


 下载:
下载:
