Gimli/Xoodoo密码算法的不可能差分分析

樊婷; 韦永壮; 李灵琛

doi:10.11999/JEIT221038

Gimli/Xoodoo密码算法的不可能差分分析

doi: 10.11999/JEIT221038

桂林电子科技大学广西密码学与信息安全重点实验室桂林 541004

基金项目: 国家自然科学基金(61872103, 62162016)，广西自然科学基金创新研究团队项目 (2019GXNSFGA245004)

详细信息

作者简介:
樊婷：女，博士生，研究方向为分组密码算法设计与分析

韦永壮：男，教授，博士生导师，研究方向为密码函数、对称密码算法设计与分析

李灵琛：女，博士，硕士生导师，研究方向为分组密码算法设计与分析

通讯作者:
韦永壮　walker_wyz@guet.edu.cn

中图分类号: TN918
计量
- 文章访问数: 549
- HTML全文浏览量: 322
- PDF下载量: 89
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-08
- 修回日期: 2022-11-24
- 网络出版日期: 2022-12-01
- 刊出日期: 2023-10-31

Impossible Differential Cryptanalysis on Gimli/Xoodoo Ciphers

Guangxi Key Laboratory of Cryptography and Information Security, Guilin University of Electronic Technology, Guilin 541004, China

Funds: The National Natural Science Foundation of China (61872103, 62162016), The Innovation Research Team Project of Guangxi Natural Science Foundation (2019GXNSFGA245004)

摘要

摘要: 大状态轻量级分组密码Gimli和Xoodoo具备逻辑门较少﹑低功耗和快速加密等诸多优点，备受业界关注。Gimli和Xoodoo算法均基于384 bit置换，大状态增加了对其安全性分析的困难性。该文通过引入AND、OR操作与S盒之间的等价表示，构建了Gimli和Xoodoo不可能差分区分器自动化搜索模型。进一步，为了验证不可能差分区分器的正确性，提出基于“二分法”的不可能差分区分器矛盾点检测新方法。结果表明：该文搜索并验证得到Gimli算法10轮不可能差分区分器以及Xoodoo算法4轮不可能差分区分器。特别地，Gimli算法不可能差分区分器轮数较已有结果提高了3轮。
- 不可能差分分析 /
- 自动化分析 /
- Gimli /
- Xoodoo
Abstract: Gimli and Xoodoo are large state lightweight block ciphers that have many advantages such as fewer logic gates, low power consumption and fast encryption, and have attracted much attention on the industry. Both are based on 384 bit permutation, while the large state can lead to the increase of difficulty of security analysis. In this paper, the equivalent representations of the AND, OR and S-boxes operations are introduced. And the automatic search model of the impossible differential distinguisher of Gimli and Xoodoo are constructed. Furthermore, a new technique based on "bisection method" is proposed to detect the contradiction for the impossible differential distinguisher, which is used to verify the correctness of the distinguisher. The results show that the impossible differential distinguishers of 10-round Gimli and 4-round Xoodoo are obtained and verified in this paper. Especially, the new impossible differential distinguisher of Gimli is increased by 3 rounds compared with the existing results.
- Impossible differential cryptanalysis /
- Automatic cryptanalysis /
- Gimli /
- Xoodoo

HTML全文

图 1 Gimli状态矩阵

下载: 全尺寸图片幻灯片

图 2 Xoodoo状态矩阵

下载: 全尺寸图片幻灯片

图 3 Gimli置换SP盒等价表示

下载: 全尺寸图片幻灯片

图 4 Gimli的10轮不可能差分区分器矛盾点

下载: 全尺寸图片幻灯片

表 1 符号说明

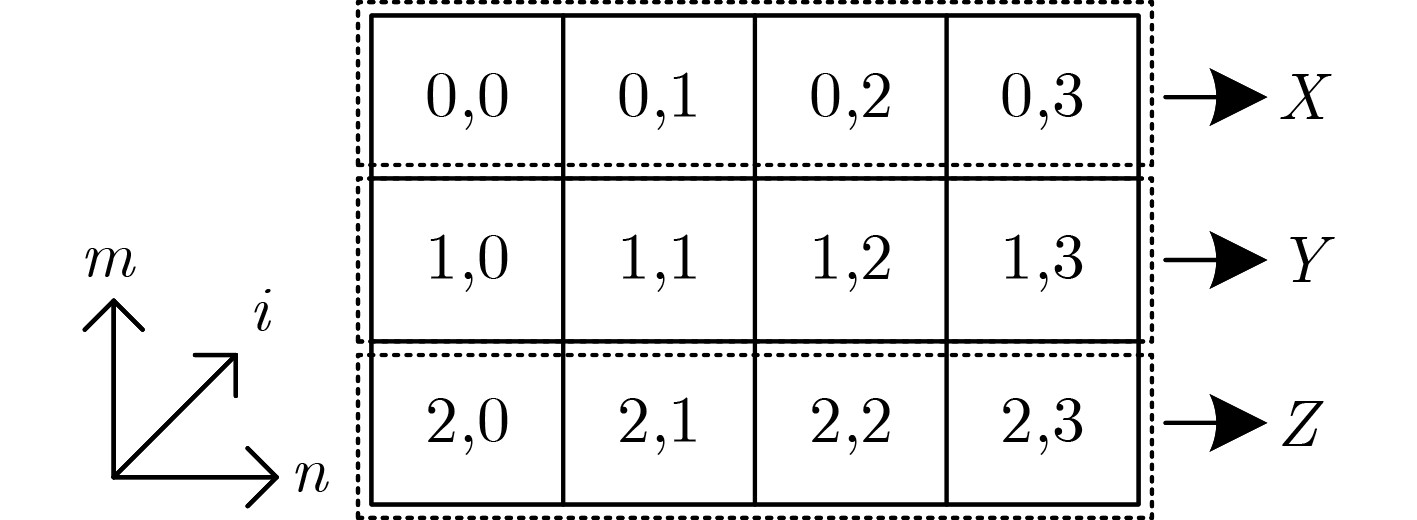
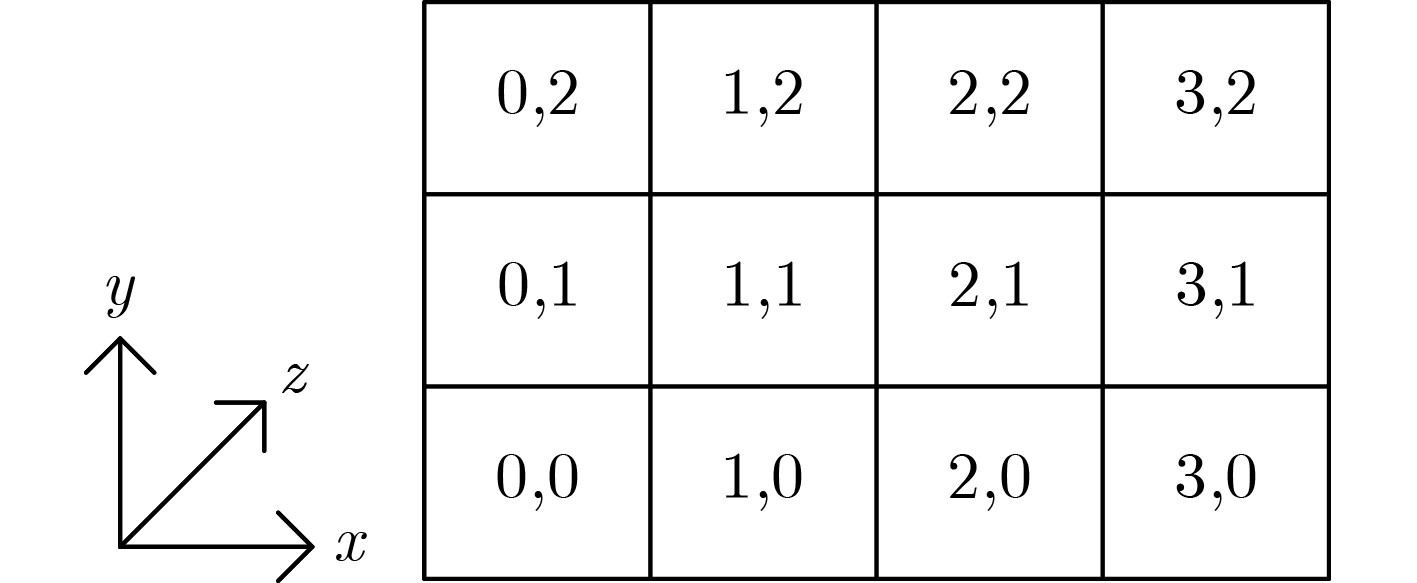
符号	说明	符号	说明
${\bf{SG}}$	Gimli算法输入状态	$ \wedge $	与运算
$\Delta {\bf{SG}}$	Gimli算法状态差分	$ \vee $	或运算
$ {\bf{SX}} $	Xoodoo算法输入状态	$ \lt \lt $	左移
$ \Delta {\bf{SX}} $	Xoodoo算法状态差分	$ \lt \lt \lt $	循环左移
${\Delta _{{\rm{in}}} }\not \to {\Delta _{{\rm{out}}} }$	${\Delta _{{\rm{in}}} }$不能传播到${\Delta _{{\rm{out}}} }$	$ \oplus $	异或运算

下载: 导出CSV

算法1　Gimli算法
$ {{\bf{SG}}_{0,n}} = X, $$ {{\bf{SG}}_{1,n}} = Y, $${ {\bf{SG} }_{2,n} } = {\boldsymbol{Z}}(0 \le n \le 3)$
对$ r = 24,23, \cdots ,1 $执行：
${\boldsymbol{X}} \leftarrow {\boldsymbol{X}} \lt \lt \lt 24,$${\boldsymbol{Y}} \leftarrow {\boldsymbol{Y}} \lt \lt \lt 9,$$ Z \leftarrow Z $　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　循环移位
${\bf{SG} }' \leftarrow {\bf{SP} }({\boldsymbol{X} },{\boldsymbol{Y} },{\boldsymbol{Z} })$　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 SP盒
若$ r\text{mod} 4 = 0 $，执行${\bf{SG} }'' \leftarrow {\rm{Small}} - {\rm{Swap}}({\bf{SG}})$　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　交换操作
若$ r\text{mod} 4 = 2 $，执行${\bf{SG}}'' \leftarrow {\rm{Big}} - {\rm{Swap}}({\bf{SG}})$
若$ r\text{mod} 4 = 0 $，执行$ {{\bf{SG}}''_{0,0}} \leftarrow {{\bf{SG}}''_{0,0}} \oplus 0x9e37790 \oplus r $　　　　　　　　　　　　　　　　　　　　　　　　　　　异或轮常数
结束，返回Gimli$({\bf{SG}}) = {\bf{SG}}''$

下载: 导出CSV

表 2 S1, S2和S3盒置换表3 bit输出

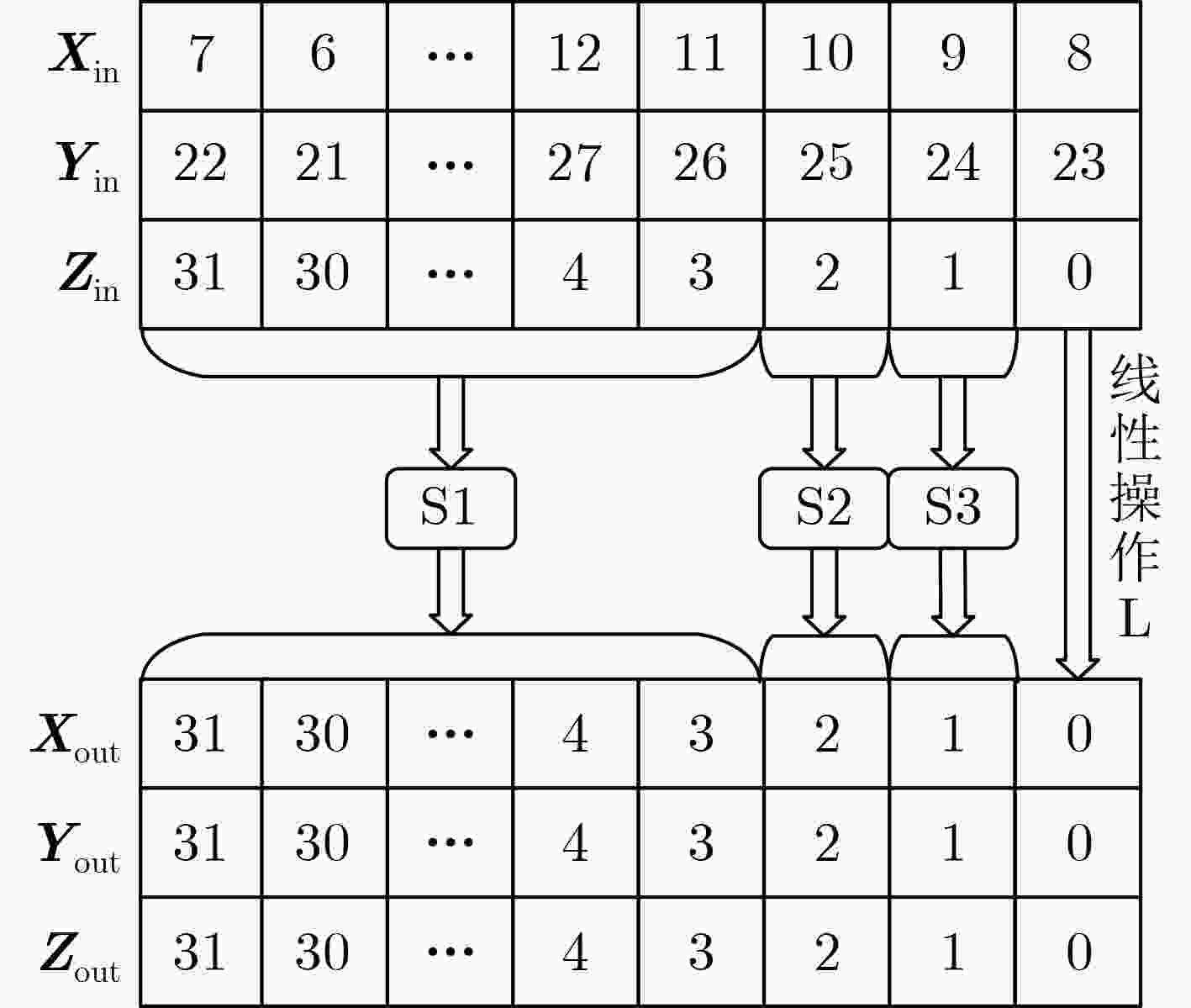
S盒	3 bit输出
S1 =	[0, 0, 0, 1, 1, 1, 1, 0, 6, 6, 6, 7, 7, 7, 7, 6, 2, 2, 2, 3, 3, 3, 3, 2, 6, 6, 6, 7, 7, 7, 7, 6, 3, 3, 3, 2, 2, 2, 2, 3, 5, 5, 5, 4, 4, 4, 4, 5, 1, 1, 1, 0, 0, 0, 0, 1, 5, 5, 5, 4, 4, 4, 4, 5, 0, 0, 0, 1, 1, 1, 1, 0, 6, 6, 6, 7, 7, 7, 7, 6, 2, 2, 2, 3, 3, 3, 3, 2, 6, 6, 6, 7, 7, 7, 7, 6, 3, 3, 3, 2, 2, 2, 2, 3, 5, 5, 5, 4, 4, 4, 4, 5, 1, 1, 1, 0, 0, 0, 0, 1, 5, 5, 5, 4, 4, 4, 4, 5, 0, 0, 0, 1, 1, 1, 1, 0, 6, 6, 6, 7, 7, 7, 7, 6, 2, 2, 2, 3, 3, 3, 3, 2, 6, 6, 6, 7, 7, 7, 7, 6, 3, 3, 3, 2, 2, 2, 2, 3, 5, 5, 5, 4, 4, 4, 4, 5, 1, 1, 1, 0, 0, 0, 0, 1, 5, 5, 5, 4, 4, 4, 4, 5, 4, 4, 4, 5, 5, 5, 5, 4, 2, 2, 2, 3, 3, 3, 3, 2, 6, 6, 6, 7, 7, 7, 7, 6, 2, 2, 2, 3, 3, 3, 3, 2, 7, 7, 7, 6, 6, 6, 6, 7, 1, 1, 1, 0, 0, 0, 0, 1, 5, 5, 5, 4, 4, 4, 4, 5, 1, 1, 1, 0, 0, 0, 0, 1, 6, 6, 6, 7, 7, 7, 7, 6, 0, 0, 0, 1, 1, 1, 1, 0, 4, 4, 4, 5, 5, 5, 5, 4, 0, 0, 0, 1, 1, 1, 1, 0, 5, 5, 5, 4, 4, 4, 4, 5, 3, 3, 3, 2, 2, 2, 2, 3, 7, 7, 7, 6, 6, 6, 6, 7, 3, 3, 3, 2, 2, 2, 2, 3, 6, 6, 6, 7, 7, 7, 7, 6, 0, 0, 0, 1, 1, 1, 1, 0, 4, 4, 4, 5, 5, 5, 5, 4, 0, 0, 0, 1, 1, 1, 1, 0, 5, 5, 5, 4, 4, 4, 4, 5, 3, 3, 3, 2, 2, 2, 2, 3, 7, 7, 7, 6, 6, 6, 6, 7, 3, 3, 3, 2, 2, 2, 2, 3, 6, 6, 6, 7, 7, 7, 7, 6, 0, 0, 0, 1, 1, 1, 1, 0, 4, 4, 4, 5, 5, 5, 5, 4, 0, 0, 0, 1, 1, 1, 1, 0, 5, 5, 5, 4, 4, 4, 4, 5, 3, 3, 3, 2, 2, 2, 2, 3, 7, 7, 7, 6, 6, 6, 6, 7, 3, 3, 3, 2, 2, 2, 2, 3, 2, 2, 2, 3, 3, 3, 3, 2, 4, 4, 4, 5, 5, 5, 5, 4, 0, 0, 0, 1, 1, 1, 1, 0, 4, 4, 4, 5, 5, 5, 5, 4, 1, 1, 1, 0, 0, 0, 0, 1, 7, 7, 7, 6, 6, 6, 6, 7, 3, 3, 3, 2, 2, 2, 2, 3, 7, 7, 7, 6, 6, 6, 6, 7]
S2 =	[0, 1, 6, 7, 2, 3, 6, 7, 3, 2, 5, 4, 1, 0, 5, 4, 0, 1, 6, 7, 2, 3, 6, 7, 3, 2, 5, 4, 1, 0, 5, 4, 0, 1, 6, 7, 2, 3, 6, 7, 3, 2, 5, 4, 1, 0, 5, 4, 4, 5, 2, 3, 6, 7, 2, 3, 7, 6, 1, 0, 5, 4, 1, 0, 6, 7, 0, 1, 4, 5, 0, 1, 5, 4, 3, 2, 7, 6, 3, 2, 6, 7, 0, 1, 4, 5, 0, 1, 5, 4, 3, 2, 7, 6, 3, 2, 6, 7, 0, 1, 4, 5, 0, 1, 5, 4, 3, 2, 7, 6, 3, 2, 2, 3, 4, 5, 0, 1, 4, 5, 1, 0, 7, 6, 3, 2, 7, 6]
S3 =	[0, 1, 6, 7, 2, 3, 6, 7, 3, 2, 5, 4, 1, 0, 5, 4, 6, 7, 0, 1, 4, 5, 0, 1, 5, 4, 3, 2, 7, 6, 3, 2]

下载: 导出CSV

表 3 Xoodoo算法操作$ \chi $的S盒表示

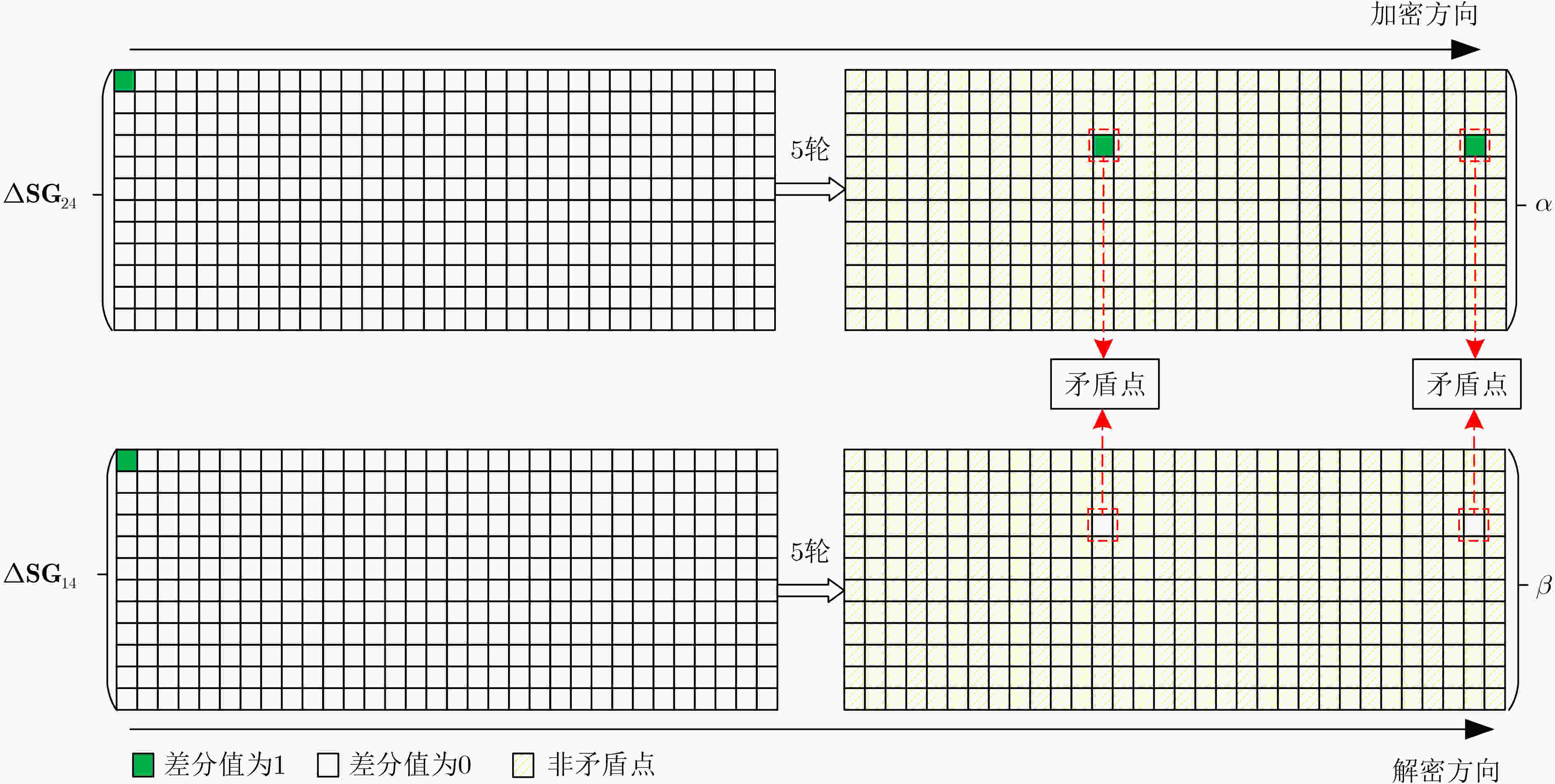
$ x $	0	1	2	3	4	5	6	7
$ S(x) $	0	5	3	2	6	1	4	7

下载: 导出CSV

算法2 新验证算法
输入轮数$ r $，分组长度轮数$ n $, ${\Delta _{{\rm{in}}} }\not \to {\Delta _{{\rm{out}}} }$, $ i = 0 $.
输出 $ q $ bit矛盾点, 集合$ {T_1} $和$ {T_2}. $
步骤1. while $i \le n:$
${\rm{mid}} = (i + n)/2$
删除等式$ {\alpha _j} = {\beta _j}, $$j \in [i,{\rm{mid}} - 1]$
if 模型有解：
$n = {\rm{mid}}$.
else if 模型无解：
$i = {\rm{mid}}$.
返回$ i,n $
步骤2. 逐条删除等式$ {\alpha _k} = {\beta _k} $, $ k \in [i,n - 1] $.
while 模型无解：
将$ {\alpha _k} $放入集合$ {T_1} $，将$ {\beta _k} $放入集合$ {T_2}. $
遍历集合$ {T_1} $,$ {T_2} $的值，在模型有解的情况下，查看二者　　　　　是否存在交集.

下载: 导出CSV

表 4 结果对比

密码算法	分析方法	轮数	文献
Gimli	不可能差分区分器	7	[12]
Gimli	不可能差分区分器	10	本文
Xoodoo	差分区分器	3	[14]
Xoodoo	不可能差分区分器	4	本文

下载: 导出CSV

参考文献(18)

[1]	NIST. Lightweight cryptography[EB/OL]. https://csrc.nist.gov/Projects/Lightweight-Cryptography, 2018.
[2]	NIST. Lightweight cryptography[EB/OL]. https://csrc.nist.gov/projects/lightweight-cryptography/round-1-candidates, 2019.
[3]	NIST. Lightweight cryptography[EB/OL]. https://csrc.nist.gov/projects/lightweight-cryptography/round-2-candidates, 2021.
[4]	BERNSTEIN D J, KÖLBL S, LUCKS S, et al. GIMLI: A cross-platform permutation[C]. The 19th International Conference on Cryptographic Hardware and Embedded Systems, Taipei, China, 2017: 299–320.
[5]	DOBRAUNIG C, EICHLSEDER M, MENDEL F, et al. ASCON v1.2: Lightweight authenticated encryption and hashing[J]. Journal of Cryptology, 2021, 34(3): 33. doi: 10.1007/s00145-021-09398-9
[6]	BEIERLE C, BIRYUKOV A, DOS SANTOS L C, et al. Lightweight AEAD and hashing using the Sparkle permutation family[J]. IACR Transactions on Symmetric Cryptology, 2020, 2020(S1): 208–261. doi: 10.13154/tosc.v2020.iS1.208-261
[7]	BERTONI G, DAEMEN J, PEETERS M, et al. Keccak[C]. The 32nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, 2013: 313–314.
[8]	DAEMEN J, HOFFERT S, PEETERS M, et al. Xoodyak, a lightweight cryptographic scheme[J]. IACR Transactions on Symmetric Cryptology, 2020, 2020(S1): 60–87. doi: 10.13154/tosc.v2020.iS1.60-87
[9]	BERNSTEIN D J, KÖLBL S, LUCKS S, et al. Gimli[EB/OL]. https://csrc.nist.gov/CSRC/media/Projects/lightweightcryptography/documents/round-2/submissions-rnd2/gimli.zip, 2019.
[10]	DAEMEN J, HOFFERT S, VAN ASSCHE G, et al. The design of Xoodoo and Xoofff[J]. IACR Transactions on Symmetric Cryptology, 2018, 2018(4): 1–38. doi: 10.13154/tosc.v2018.i4.1-38
[11]	LIU Fukang, ISOBE T, and MEIER W. Automatic verification of differential characteristics: Application to reduced Gimli[C]. The 40th Annual International Cryptology Conference, Santa Barbara, USA, 2020: 219–248.
[12]	谭豪, 申兵, 苗旭东, 等. Gimli认证加密方案的不可能差分分析[J]. 西安电子科技大学学报, 2022, 49(5): 1–9. doi: 10.19665/j.issn1001-2400.2022.05.024 TAN Hao, SHEN Bing, MIAO Xudong, et al. Impossible differential cryptanalysis of the Gimli authenticated encryption scheme[J]. Journal of Xidian University, 2022, 49(5): 1–9. doi: 10.19665/j.issn1001-2400.2022.05.024
[13]	LIU Yunwen, SUN Siwei, and LI Chao. Rotational cryptanalysis from a differential-linear perspective[C]. The 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2021: 741–770.
[14]	BELLINI E and MAKARIM R. Functional cryptanalysis: Application to reduced-round Xoodoo[EB/OL]. https://eprint.iacr.org/2022/134, 2022.
[15]	SUN Siwei, HU Lei, WANG Peng, et al. Automatic security evaluation and (related-key) differential characteristic search: Application to SIMON, PRESENT, LBlock, DES(L) and other bit-oriented block ciphers[C]. The 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, China, 2014: 158–178.
[16]	SageMath[EB/OL]. http://www.sagemath.org/index.html, 2022.
[17]	Gurobi optimizer 9.1. 2[EB/OL]. http://www.gurobi.com, 2021.
[18]	CUI Tingting, CHEN Shiyao, JIA Keting, et al. New automatic search tool for impossible differentials and zero-correlation linear approximations[EB/OL]. https://eprint.iacr.org/2016/689, 2016.