低信噪比场景下Link-16系统的联合频偏估计算法

宁晓燕; 罗海玲; 孙志国; 刁鸣

doi:10.11999/JEIT220967

低信噪比场景下Link-16系统的联合频偏估计算法

doi: 10.11999/JEIT220967

哈尔滨工程大学信息与通信工程学院哈尔滨 150001

详细信息

作者简介:
宁晓燕：女，副教授，研究方向为5G通信物理层新技术、军用数据链

罗海玲：女，硕士生，研究方向为军用数据链、认知通信

孙志国：男，教授，研究方向为新一代数据链与通信系统、认知通信防护、多维电磁频谱感知技术等

刁鸣：男，教授，研究方向为宽带信号检测、处理与识别，通信信号处理

通讯作者:
孙志国　sunzhiguo@hrbeu.edu.cn

中图分类号: TN919.3
计量
- 文章访问数: 464
- HTML全文浏览量: 644
- PDF下载量: 143
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-21
- 修回日期: 2022-12-06
- 网络出版日期: 2022-12-09
- 刊出日期: 2023-10-31

Joint Frequency Offset Estimation for Link-16 System in Low Signal-Noise Ratio Scene

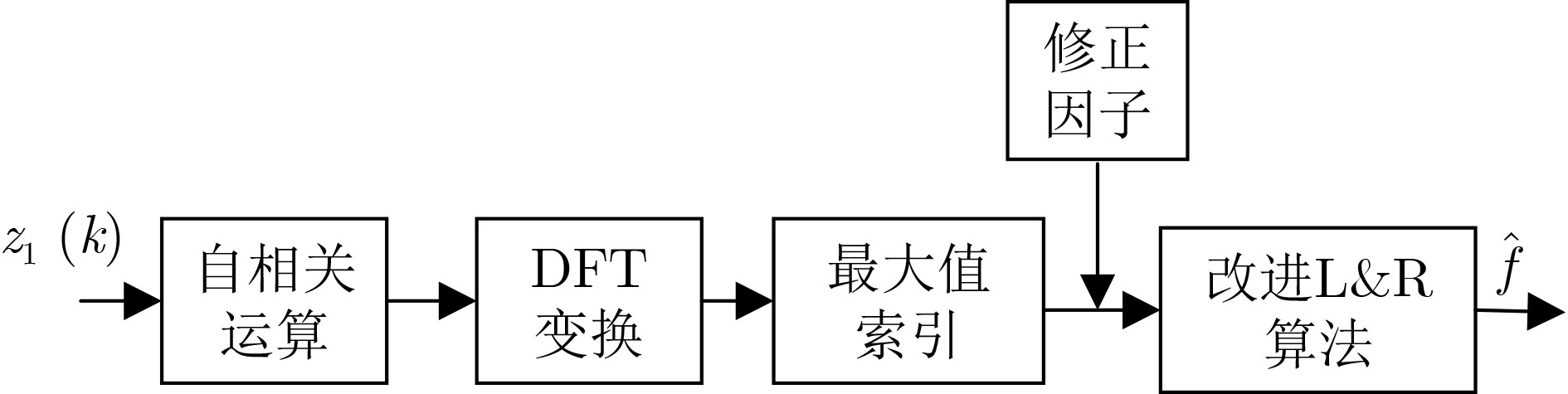
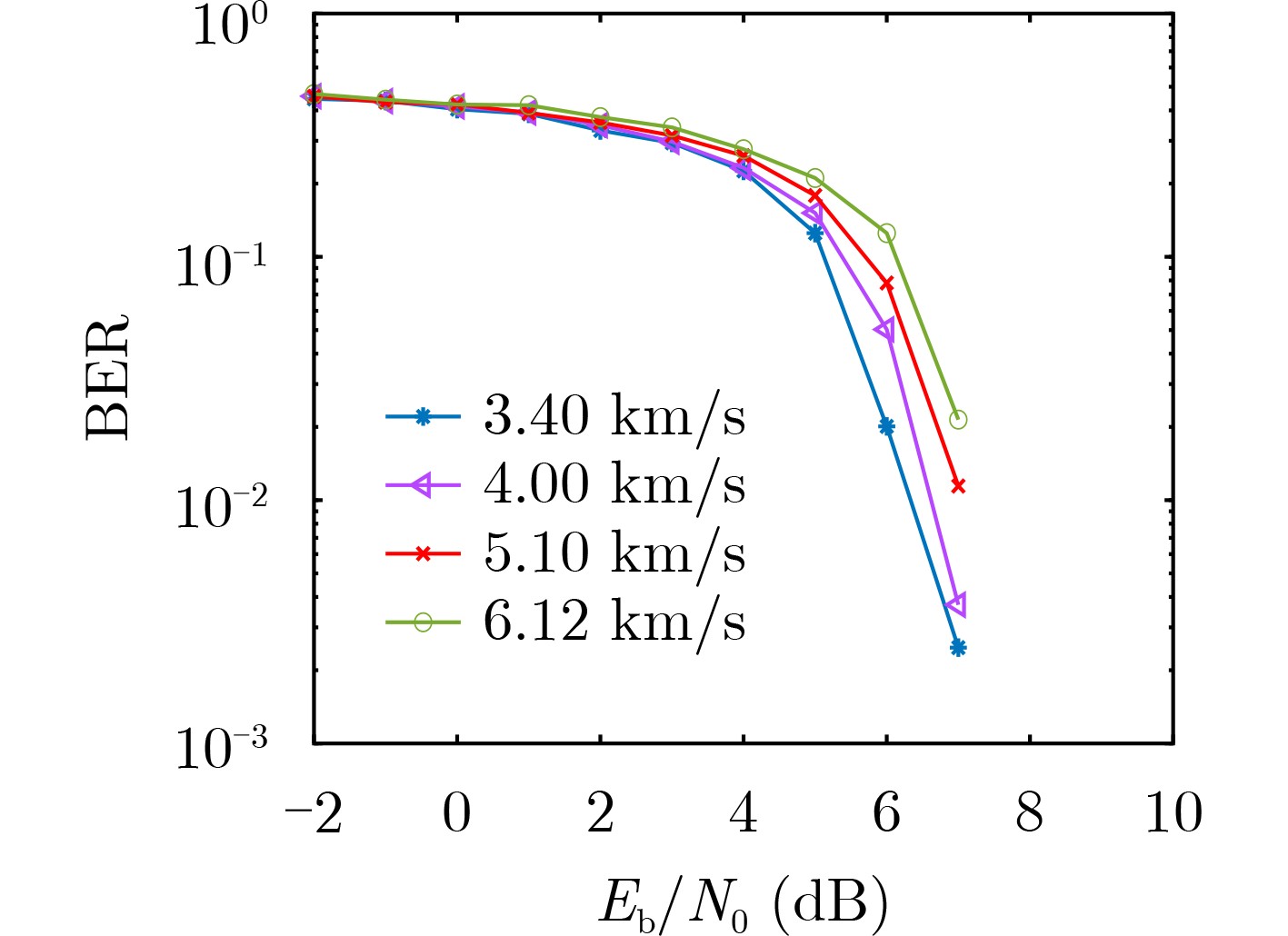
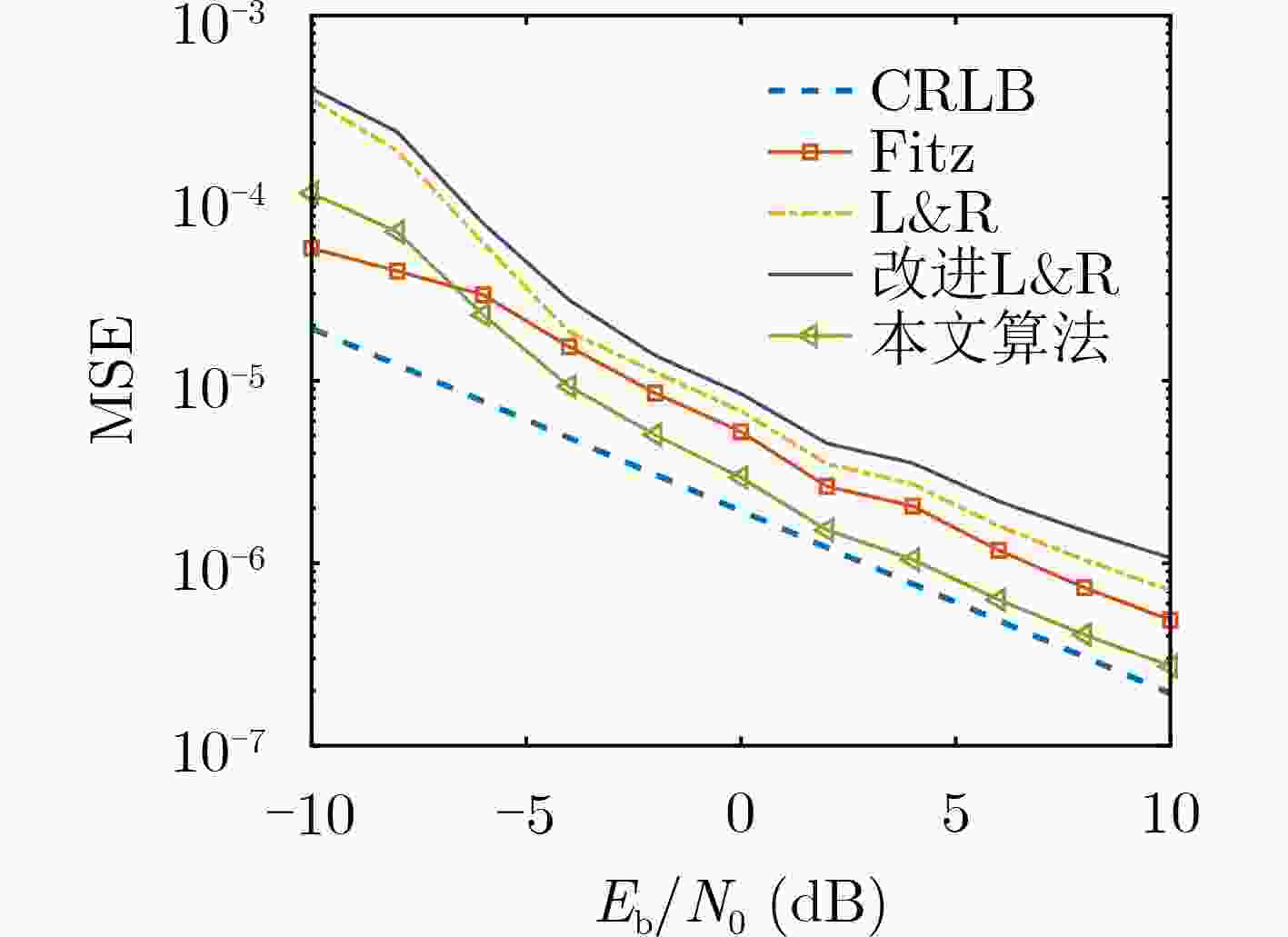
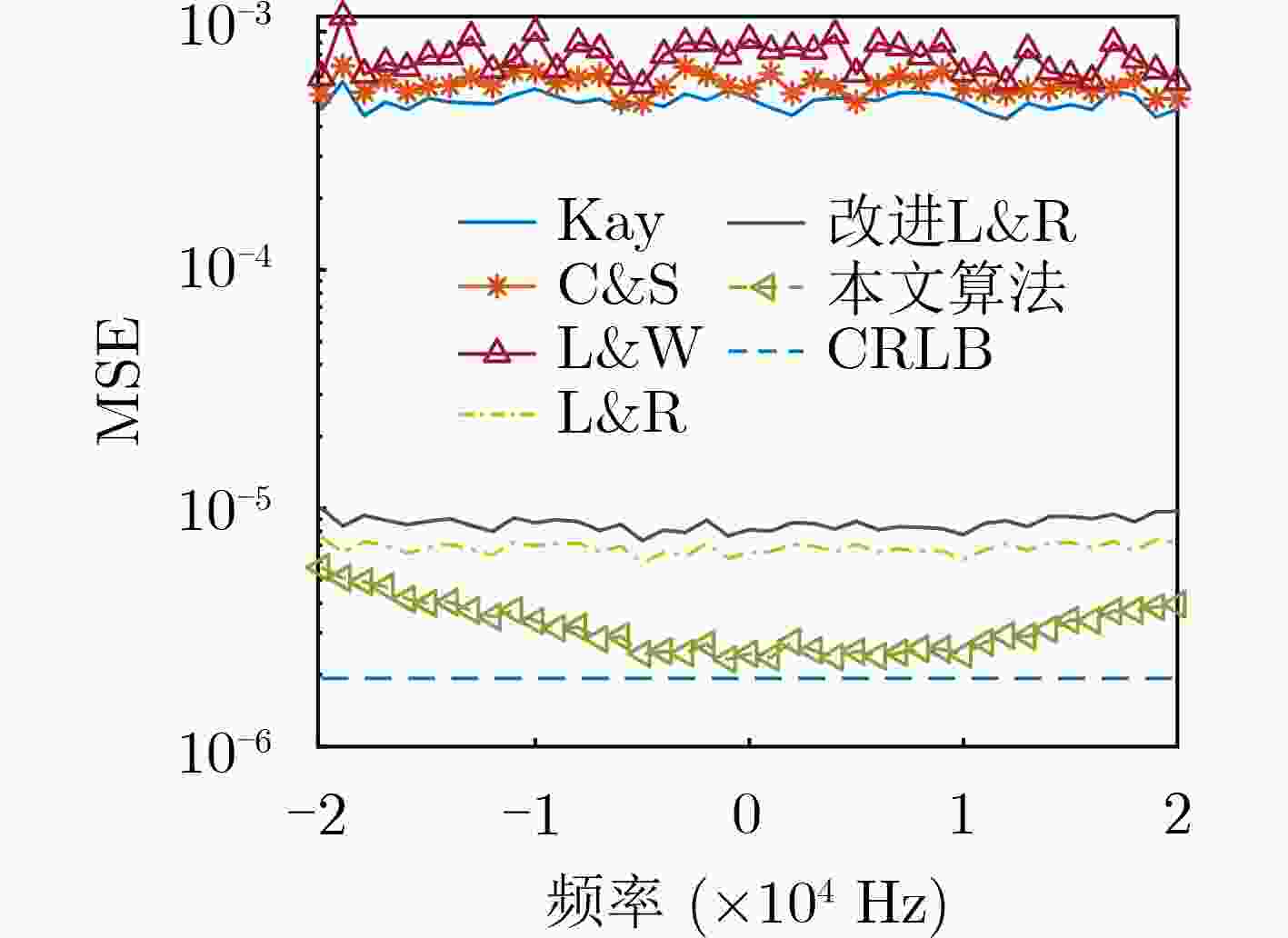
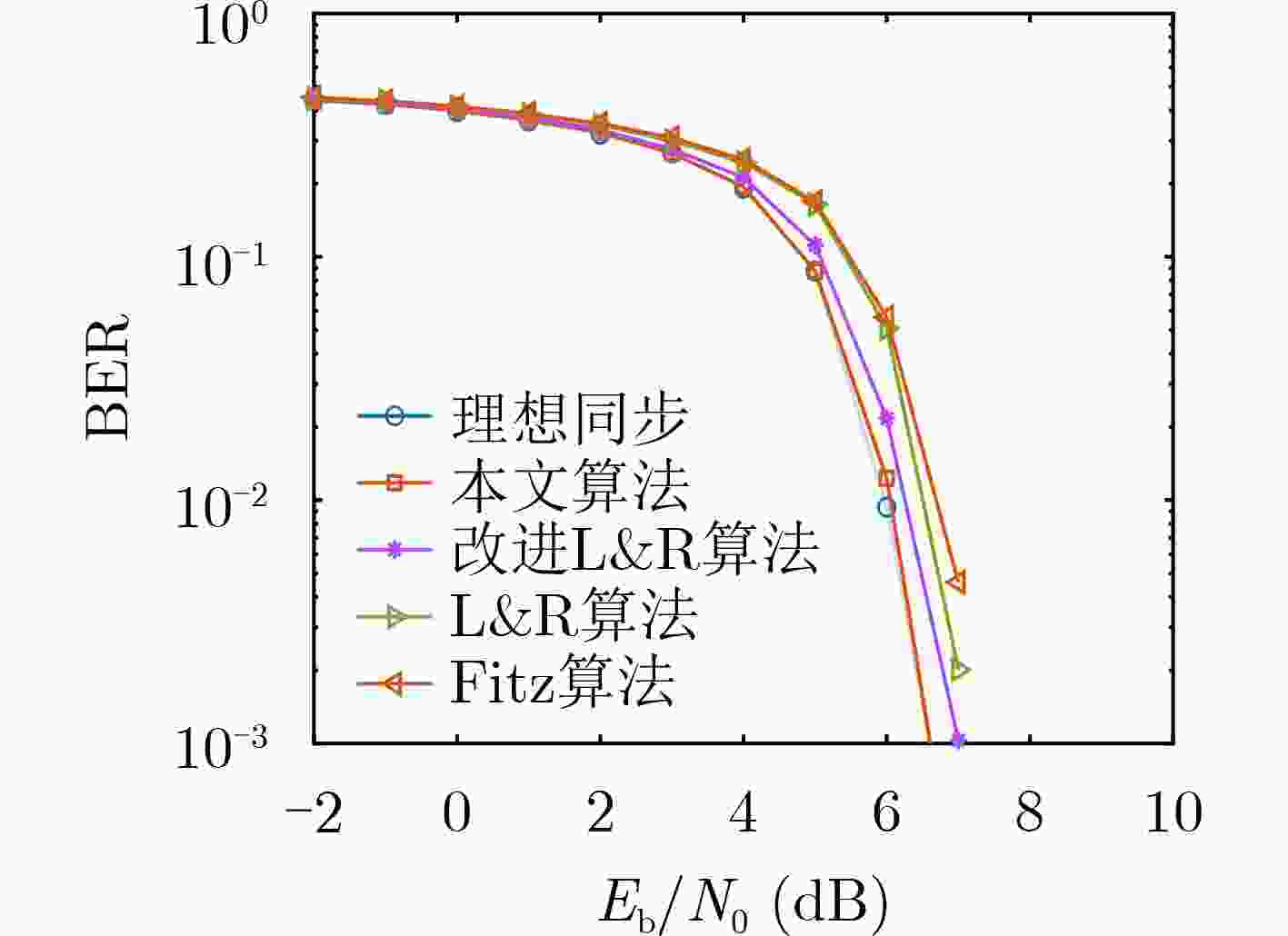
College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China

摘要

摘要: 对于Link-16数据链终端平台在低信噪比(SNR)高动态场景下的多普勒频率偏移问题，该文设计一种新的数据结构，推导了该结构下的克拉默-拉奥下界(CRLB)，并在此基础上提出一种联合频域变换与时域自相关运算的分步式频偏估计算法。其基本思想是，首先对接收信号做自相关处理，然后通过频域变换进行最大值索引，结合修正因子得到多普勒频移的粗估计值，再利用时域的改进L&R算法对接收信号进行细估计，根据两步估计算法得到最终的频偏估计值。算法应用蒙特卡罗实验仿真，仿真结果表明，与传统频偏估计算法相比，该算法的归一化均方误差更接近CRLB，在多普勒频偏为[–20 kHz, 20 kHz]时，估计精度可达10^–5。在低信噪比环境下，所提算法能达到较为理想的估计效果，适用于Link-16数据链通信。
- Link-16数据链 /
- 克拉默-拉奥下界 /
- 自相关处理 /
- 改进L&R算法 /
- 分步式估计算法
Abstract: For the Doppler frequency offset of Link-16 data link terminal platform in low Signal-Noise Ratio(SNR) and high-speed moving scene, a new data structure is designed, and a step-by-step frequency offset estimation algorithm combining frequency domain transform, and the Cramer-Rao Low Bound(CRLB) and time-domain autocorrelation is proposed on this basis. First according to the basic idea, the received signal is autocorrelated, and then the maximum index is found through frequency domain transformation. Combined with the correlation factor, the coarse estimation value of frequency offset is obtained. Then, the received signal is finely estimated by using improved L&R algorithm in time domain, and the final frequency offset estimation value is obtained according to the two-step estimation algorithm. The algorithm is simulated by Monte Carlo experiment. The simulation results show that compared with the traditional frequency offset estimation algorithm, the normalized mean square error of the algorithm is closer to CRLB, and when the Doppler frequency offset is [–20 kHz, 20 kHz], the estimation accuracy can reach 10^–5. In low SNR environment, the algorithm can achieve ideal estimation effect, which is suitable for Link-16 data link communication.
- Link-16 data link /
- Cramer-Rao Low Bound(CRLB) /
- Autocorrelation /
- Improved L&R algorithm /
- Distributed estimation algorithm

HTML全文

图 1 Link-16跳频图案

下载: 全尺寸图片幻灯片

图 2 加入导频序列的时隙结构

下载: 全尺寸图片幻灯片

图 3 加入导频序列的脉冲结构

下载: 全尺寸图片幻灯片

图 4 所提算法实现流程图

下载: 全尺寸图片幻灯片

图 5 不同信道下误码率曲线

下载: 全尺寸图片幻灯片

图 6 不同飞行速度下的误码率曲线

下载: 全尺寸图片幻灯片

图 7 不同估计算法的均方误差

下载: 全尺寸图片幻灯片

图 8 不同估计算法的估计范围

下载: 全尺寸图片幻灯片

图 9 接收系统误码率

下载: 全尺寸图片幻灯片

表 1 仿真参数

仿真参数值

带宽 3.5 MHz
调制方式 MSK
导频长度 32
码元周期 2 µs
采样点数 200
数据速率 59.6 kbit/s

下载: 导出CSV

参考文献(17)

[1]	王旭东, 樊涛, 黄强辉, 等. 大多普勒频偏SOQPSK信号FFT引导COSTAS环载波跟踪技术[J]. 电子学报, 2016, 46(2): 491–496. doi: 10.3969/j.issn.0372-2112.2016.02.034 WANG Xudong, FAN Tao, HUANG Qianghui, et al. SOQPSK carrier tracking technology with large Doppler frequency offset based on FFT guided Costas loop[J]. Acta Electronica Sinica, 2016, 46(2): 491–496. doi: 10.3969/j.issn.0372-2112.2016.02.034
[2]	KAY S. A fast and accurate single frequency estimator[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(12): 1987–1990. doi: 10.1109/29.45547
[3]	FITZ M P. Further results in the fast estimation of a single frequency[J]. IEEE Transactions on Communications, 1994, 42(234): 862–864. doi: 10.1109/TCOMM.1994.580190
[4]	LUISE M and REGGIANNINI R. Carrier frequency recovery in all-digital modems for burst-mode transmissions[J]. IEEE Transactions on Communications, 1995, 43(2/4): 1169–1178. doi: 10.1109/26.380149
[5]	MENGALI U and MORELLI M. Data-aided frequency estimation for burst digital transmission[J]. IEEE Transactions on Communications, 1997, 43(1): 23–25. doi: 10.1109/26.554282
[6]	孙锦华, 石静静. iNET系统多径衰落信道下的两步频偏估计算法[J]. 电子学报, 2019, 47(7): 1506–1511. doi: 10.3969/j.issn.0372-2112.2019.07.014 SUN Jinhua and SHI Jingjing. A two step frequency offset estimation algorithm using the INET preamble in multipath fading channels[J]. Acta Electronica Sinica, 2019, 47(7): 1506–1511. doi: 10.3969/j.issn.0372-2112.2019.07.014
[7]	ZHANG Qixun, SUN Huiqing, FENG Zhiyong, et al. Data-aided Doppler frequency shift estimation and compensation for UAVs[J]. IEEE Internet of Things Journal, 2020, 7(1): 400–415. doi: 10.1109/jiot.2019.2943608
[8]	ZENG Rong, HUANG Hanbing, YANG Liuqing, et al. Joint estimation of frequency offset and Doppler shift in high mobility environments based on orthogonal angle domain subspace projection[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2254–2266. doi: 10.1109/TVT.2017.2766887
[9]	许凯嘉, 黄巍, 查雨希, 等. 基于空时分组码的Link-16全空域增强传输方案[J]. 指挥与控制学报, 2021, 7(1): 70–75. doi: 10.3969/j.issn.2096-0204.2021.01.0070 XU Kaijia, HUANG Wei, ZHA Yuxi, et al. Link-16 full airspace enhanced transmission scheme based on space-time block code[J]. Journal of Command and Control, 2021, 7(1): 70–75. doi: 10.3969/j.issn.2096-0204.2021.01.0070
[10]	张嘉怡, 余忠洋, 朱敏, 等. 低轨卫星通信中SCMA系统载波同步算法设计[J]. 系统工程与电子技术, 2021, 43(5): 1354–1360. doi: 10.12305/j.issn.1001-506X.2021.05.24 ZHANG Jiayi, YU Zhongyang, ZHU Min, et al. Design of carrier synchronization algorithm for SCMA system in LEO satellite communication[J]. Systems Engineering and Electronics, 2021, 43(5): 1354–1360. doi: 10.12305/j.issn.1001-506X.2021.05.24
[11]	赵文超, 刘祖深, 许虎. 基于DMRS联合频偏估计方法及应用[J]. 电子测量与仪器学报, 2021, 35(11): 170–176. doi: 10.13382/j.jemi.B2104019 ZHAO Wenchao, LIU Zushen, and XU Hu. Method and application of joint frequency offset estimation based on DMRS[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(11): 170–176. doi: 10.13382/j.jemi.B2104019
[12]	吕娜, 张岳彤, 陈柯帆, 等. 数据链理论与系统[M]. 2版. 北京: 电子工业出版社, 2018: 130–131. LV Na, ZHANG Yuetong, CHEN Kefan, et al. Theory and System of Data Link[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2018: 130–131.
[13]	赵陆文, 张北江, 缪志敏, 等. 低信噪比突发信号载波频偏估计算法[J]. 系统工程与电子技术, 2015, 37(12): 2848–2852. doi: 10.3969/j.issn.1001-506X.2015.12.28 ZHAO Luwen, ZHANG Beijiang, MIAO Zhimin, et al. Carrier frequency offset estimation algorithm for burst and low SNR signal[J]. Systems Engineering and Electronics, 2015, 37(12): 2848–2852. doi: 10.3969/j.issn.1001-506X.2015.12.28
[14]	蒋占军, 刘庆达, 张鈜, 等. 高速移动通信系统中OTFS分数多普勒信道估计加窗研究[J]. 电子与信息学报, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561 JIANG Zhanjun, LIU Qingda, ZHANG Hong, et al. Study on OTFS fractional Doppler channel estimation and windowing in high-speed mobile communication systems[J]. Journal of Electronics &Information Technology, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561
[15]	关磊, 司江勃, 李赞, 等. 高动态环境下联合导频与Viterbi的同步技术[J]. 西安电子科技大学学报, 2022, 49(2): 21–28. doi: 10.19665/j.issn1001-2400.2022.02.003 GUAN Lei, SI Jiangbo, LI Zan, et al. Joint pilot and Viterbi decoding synchronization technology in high-dynamic environments[J]. Journal of Xidian University, 2022, 49(2): 21–28. doi: 10.19665/j.issn1001-2400.2022.02.003
[16]	SERGIENKO A B and BARANOV M A. Application of modified luise and reggiannini method for blind estimation of frequency offset for QAM signals[C]. 2020 Wave Electronics and its Application in Information and Telecommunication Systems, St. Petersburg, Russia, 2020: 1–4.
[17]	石璟, 张朝阳, 储珊, 等. 一种TD-SCDMA载波频偏与信道联合估计算法[J]. 电子与信息学报, 2006, 28(11): 2099–2102. SHI Jing, ZHANG Zhaoyang, CHU Shan, et al. A channel and carrier frequency offset joint estimation algorithm for TD-SCDMA[J]. Journal of Electronics &Information Technology, 2006, 28(11): 2099–2102.