An Adaptive Weak Target Detection Method Using Joint Detection and Tracking for Compact High Frequency Surface Ware Radar
-
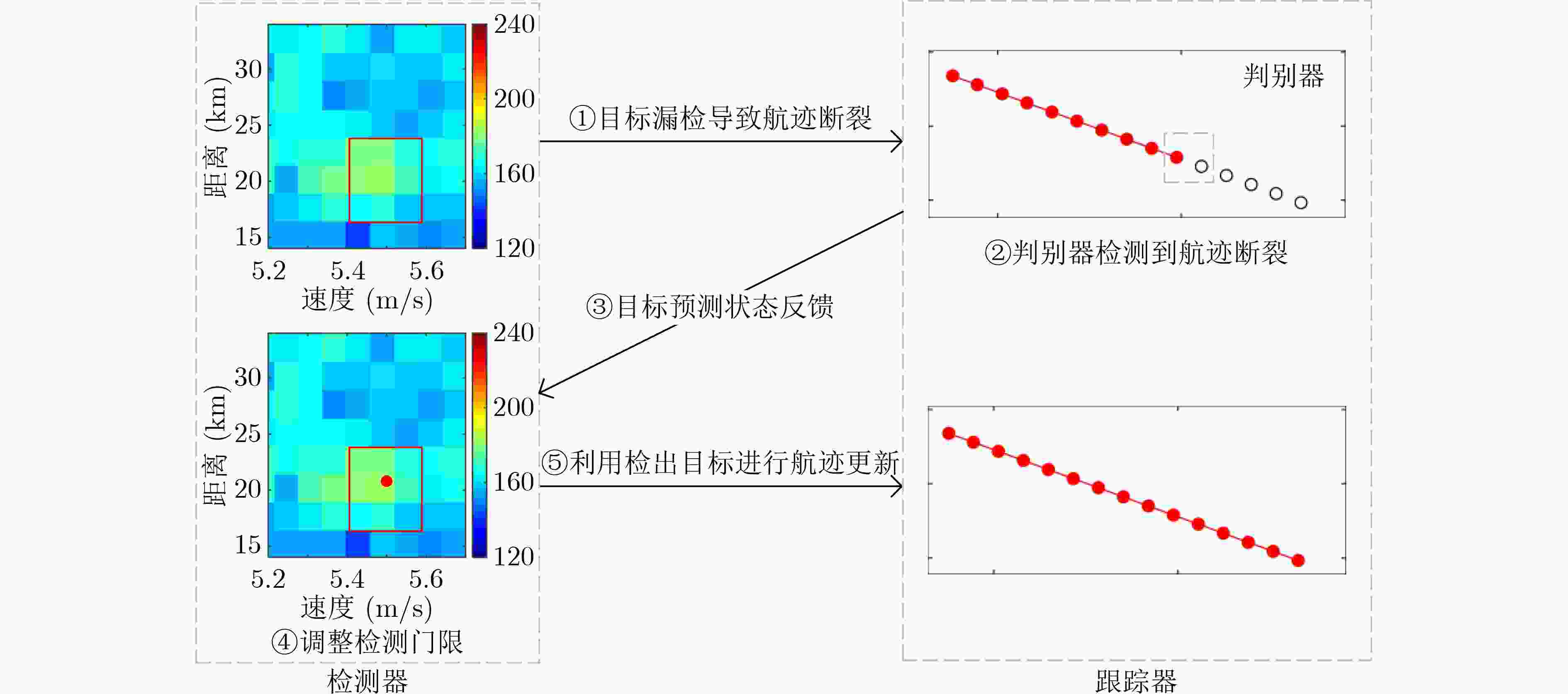
摘要: 紧凑型地波雷达发射功率低、回波信噪比低,目标检测难度大,在目标跟踪时由于目标漏检经常出现航迹断裂。为了提升其目标检测性能,提出了一种基于检测-跟踪联动的弱目标自适应检测方法。当跟踪器检测到目标航迹无法关联到新点迹时,将当前目标预测状态反馈至检测器;检测器在距离-多普勒谱上建立局部检测波门,采用二元假设检验法感知波门内的检测背景,根据不同的检测背景选取适用的检测门限调整方法,降低恒虚警检测的门限,判定是否有弱目标被检出。若能够检出目标,对其进行测向后将新点迹发送至跟踪器进行处理。利用实测数据开展了目标检测与跟踪实验,结果表明:与先检测后跟踪方法相比,该方法得到的目标航迹时长增加了29.76%,平均延长了19.25 min。Abstract: The low transmission power and low signal-to-noise ratio increase the challenges of target detection for compact High-Frequency Surface Wave Radar (HFSWR). Track fragmentation often occurs due to missed detections during the tracking procedure. An adaptive weak target detection method using joint detection and tracking is suggested to enhance its detection performance. The tracker will communicate back the current target prediction state to the detector when it discovers that a target track can not be connected to any new plot. The detector establishes a local detection gate on the Range-Doppler (R-D) spectrum, and the detection background is perceived using the binary hypothesis test. According to the detected background, an appropriate detection threshold adjustment method is used to lower the Constant False Alarm Rate (CFAR) detection threshold and determines whether a weak target can be detected. The newly generated plot is obtained after the azimuth estimate and transmitted to the tracker for additional processing if a target is detected. The experimental results with field data reveal that the track length obtained by the proposed method is 29.76% longer than that of the detection before tracking methods, and the tracking time increases by 19.25 minutes on average.
-
算法1 基于梯度下降法的检测门限调整方法步骤 输入:门限因子的初值${T_0}$与终值$\hat T$、梯度下降步长$\alpha $、参考单元
个数$N$、$k + 1$时刻的R-D谱数据、初始虚警率$ {P_{{{\text{f}}_0}}} $、方位角预测
值$\theta _{k + 1}^{\text{p}}$及点迹-航迹关联波门的方位角阈值${ {\boldsymbol{\varTheta } }_{ {\text{th} } } }$输出:新检出目标点迹${\boldsymbol{x}}_{k + 1}^{\text{m}} = {\left[ {v_{k + 1}^{\text{m}},r_{k + 1}^{\text{m}},\theta _{k + 1}^{\text{m}}} \right]^{\text{T}}}$(上角标
${\text{m}}$表示量测状态)算法步骤: (1) 初始化迭代次数$n = 0$,$T = {T_0}$; (2) 根据式(8)计算函数$T$在${P_{{{\text{f}}_n}}}$处的梯度$\nabla T$: $\nabla T = \dfrac{ {\partial T} }{ {\partial {P_{ { {\text{f} }_n} } } }} = - {P_{ { {\text{f} }_n} } }^{\left( { - \frac{1}{N} - 1} \right)}$ (8) (3) 根据式(9)求得当前$T$的下降距离$d$: $ d = - \alpha \times \nabla T $ (9) (4) $n = n + 1$,将门限因子$T$更新为$T = T - d$,并根据式(2)计
算$T$对应的虚警率${P_{{{\text{f}}_n}}}$;(5) 判断是否满足$T \le \hat T$。若满足,则终止算法;若未满足,则
转入步骤(6);(6) 采用门限因子$T$对应的检测门限在当前R-D谱数据的局部检
测波门内进行目标检测,若无新目标检出,则转入步骤(2);若
有新目标检出,则转入步骤(7);(7) 对新检出的目标进行方位角估计,判断方位角$\theta _{k + 1}^{\text{m}}$是否满足
$\left| {\theta _{k + 1}^{\text{m} } - \theta _{k + 1}^{\text{p} } } \right| < { {\boldsymbol{\varTheta } }_{ {\text{th} } } }$,若满足,则认为该目标为与断裂航迹匹
配的漏检目标,并输出新检出的目标点迹
${\boldsymbol{x}}_{k + 1}^{\text{m}} = {\left[ {v_{k + 1}^{\text{m}},r_{k + 1}^{\text{m}},\theta _{k + 1}^{\text{m}}} \right]^{\text{T}}}$;若不满足,则转入步骤(2)。表 1 基于实测数据的航迹跟踪时长对比(min)
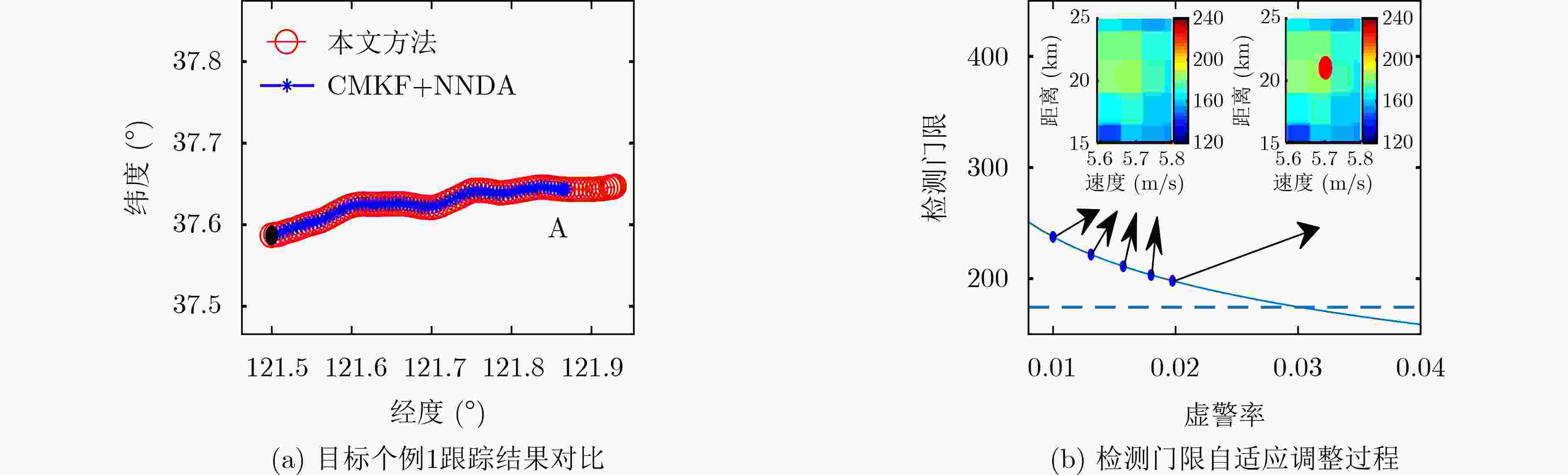
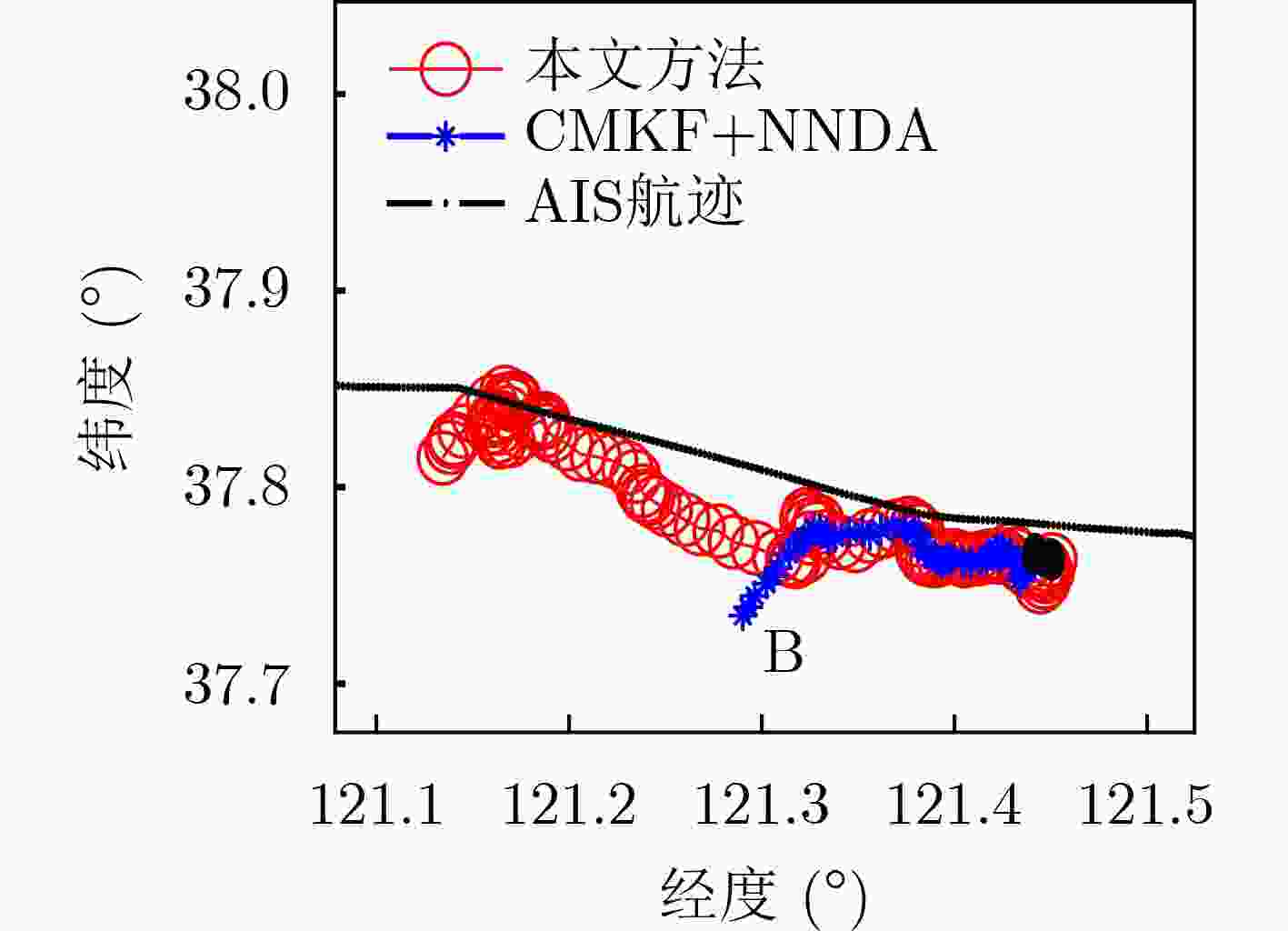
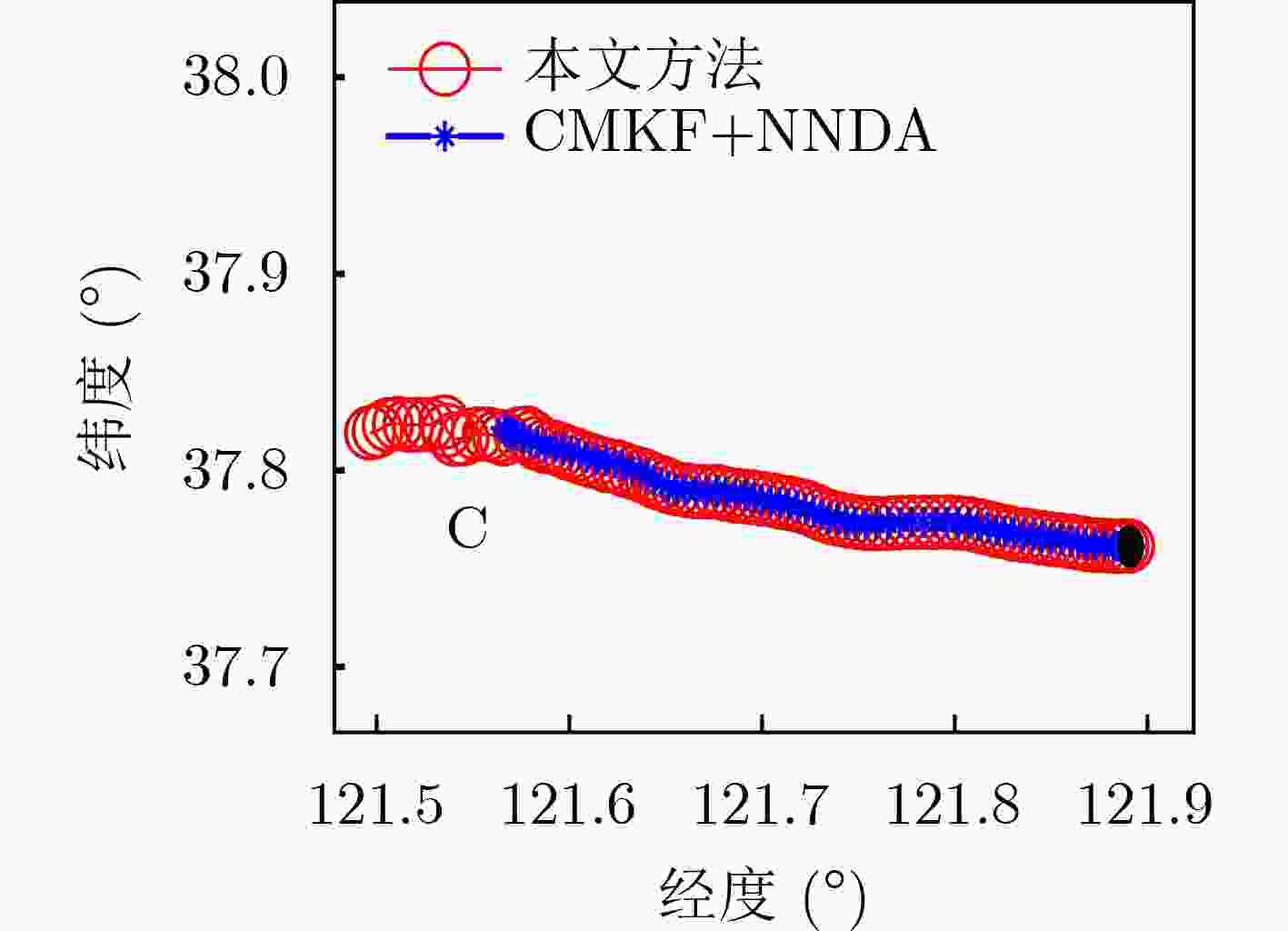
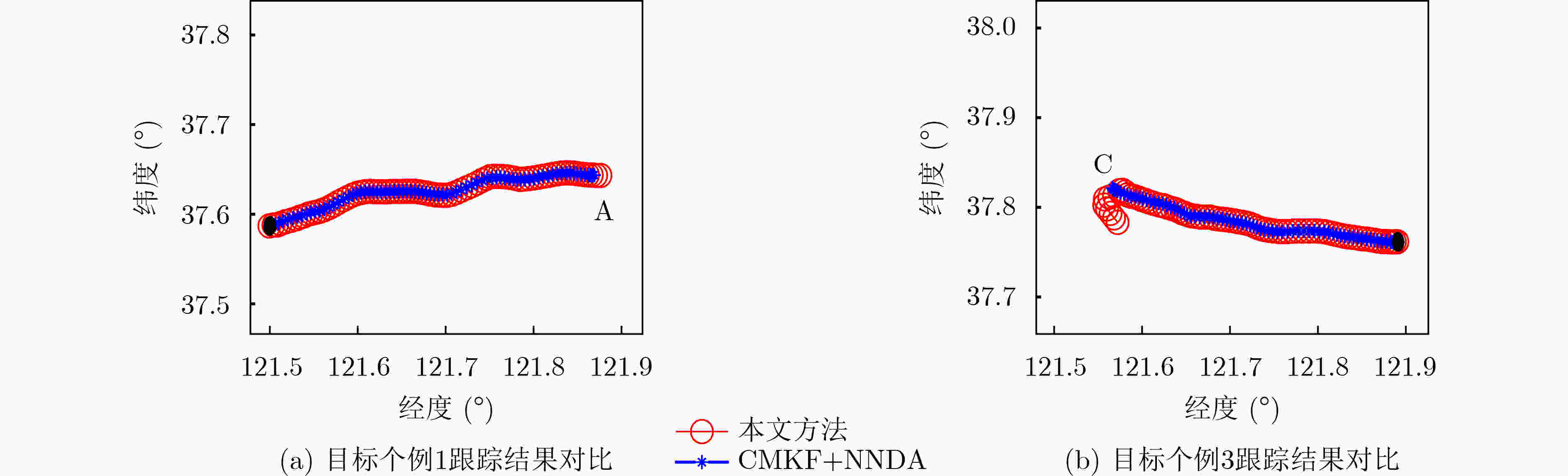
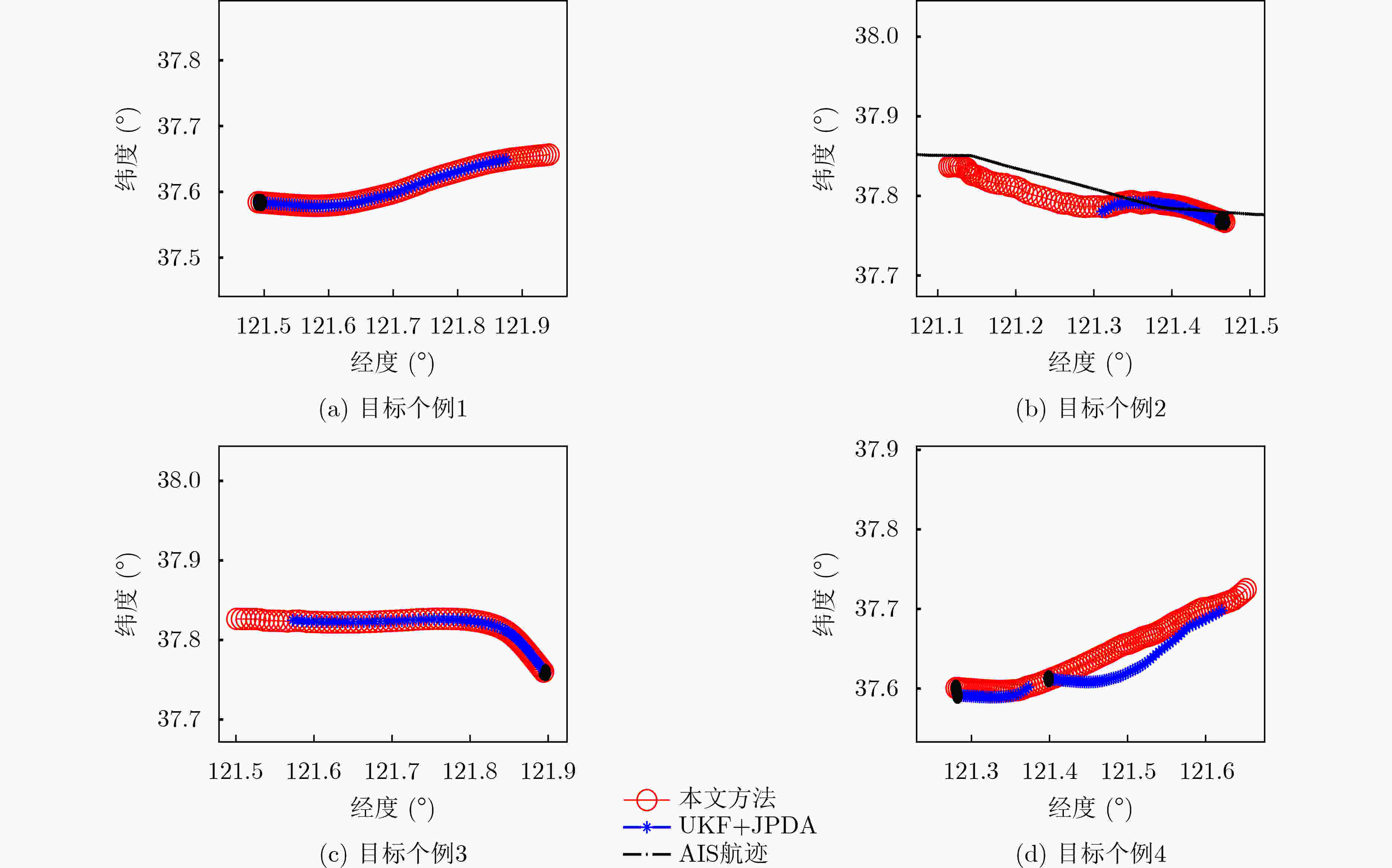
方法 目标个例1 目标个例2 目标个例3 目标个例4 CMKF+NNDA方法 78 57 73 100 本文方法 91 102 85 107 -
[1] SUN Weifeng, JI Mengjie, HUANG Weimin, et al. Vessel tracking using bistatic compact HFSWR[J]. Remote Sensing, 2020, 12(8): 1266. doi: 10.3390/rs12081266 [2] 戴永寿, 马鹏, 孙伟峰, 等. 基于JVC的紧凑型地波雷达海上目标点迹-航迹最优关联方法[J]. 电子与信息学报, 2021, 43(10): 2832–2839. doi: 10.11999/JEIT200604DAI Yongshou, MA Peng, SUN Weifeng, et al. An optimal plot-to-track association method based on JVC algorithm for maritime target with compact HFSWR[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2832–2839. doi: 10.11999/JEIT200604 [3] SUN Weifeng, HUANG Weimin, JI Yonggang, et al. A vessel azimuth and course joint re-estimation method for compact HFSWR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 1041–1051. doi: 10.1109/TGRS.2019.2943065 [4] SUN Weifeng, PANG Zhenzhen, HUANG Weimin, et al. Vessel velocity estimation and tracking from Doppler echoes of T/R-R composite compact HFSWR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 4427–4440. doi: 10.1109/JSTARS.2021.3071625 [5] 杨威, 付耀文, 潘晓刚, 等. 弱目标检测前跟踪技术研究综述[J]. 电子学报, 2014, 42(9): 1786–1793. doi: 10.3969/j.issn.0372-2112.2014.09.019YANG Wei, FU Yaowen, PAN Xiaogang, et al. Track-before-detect technique for dim targets: An overview[J]. Acta Electronica Sinica, 2014, 42(9): 1786–1793. doi: 10.3969/j.issn.0372-2112.2014.09.019 [6] 王国宏, 李岳峰, 于洪波, 等. 三维空间中高超声速目标修正三级Hough变换-检测前跟踪算法[J]. 电子与信息学报, 2018, 40(4): 890–897. doi: 10.11999/JEIT170622WANG Guohong, LI Yuefeng, YU Hongbo, et al. Modified triple-stage Hough transform track-before-detect algorithm in three-dimensional space for hypersonic target[J]. Journal of Electronics &Information Technology, 2018, 40(4): 890–897. doi: 10.11999/JEIT170622 [7] 柳超, 孙进平, 袁常顺, 等. Geodesic流多伯努利检测前跟踪方法[J]. 电子学报, 2020, 48(7): 1375–1379. doi: 10.3969/j.issn.0372-2112.2020.07.017LIU Chao, SUN Jinping, YUAN Changshun, et al. Multi-Bernoulli track-before-detect method with Geodesic flow[J]. Acta Electronica Sinica, 2020, 48(7): 1375–1379. doi: 10.3969/j.issn.0372-2112.2020.07.017 [8] 卢锦, 王鑫. 基于代价参考粒子滤波器组的检测前跟踪算法[J]. 电子与信息学报, 2021, 43(10): 2815–2823. doi: 10.11999/JEIT210234LU Jin and WANG Xin. Cost-reference particle filter bank based track-before-detecting algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2815–2823. doi: 10.11999/JEIT210234 [9] BAO Zhichao, JIANG Qiuxi, and LIU Fangzheng. Multiple model efficient particle filter based track-before-detect for maneuvering weak targets[J]. Journal of Systems Engineering and Electronics, 2020, 31(4): 647–656. doi: 10.23919/JSEE.2020.000040 [10] GROSSI E, LOPS M, and VENTURINO L. A novel dynamic programming algorithm for track-before-detect in radar systems[J]. IEEE Transactions on Signal Processing, 2013, 61(10): 2608–2619. doi: 10.1109/TSP.2013.2251338 [11] REED I S, GAGLIARDI R M, and SHAO H M. Application of three-dimensional filtering to moving target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(6): 898–905. doi: 10.1109/TAES.1983.309401 [12] YAN Bo, PAOLINI E, XU Luping, et al. A target detection and tracking method for multiple radar systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1–21. doi: 10.1109/TGRS.2022.3183387 [13] 邹鲲, 廖桂生, 李军, 等. 非高斯杂波下知识辅助检测器敏感性分析[J]. 电子与信息学报, 2014, 36(1): 181–186. doi: 10.3724/SP.J.1146.2013.00320ZOU Kun, LIAO Guisheng, LI Jun, et al. Sensitivity analysis of knowledge aided detector in non-Gaussian clutter[J]. Journal of Electronics &Information Technology, 2014, 36(1): 181–186. doi: 10.3724/SP.J.1146.2013.00320 [14] 卢术平, 宋海洋, 易伟, 等. 基于雷达知识库的知识辅助恒虚警检测算法[J]. 现代雷达, 2017, 39(6): 46–49. doi: 10.16592/j.cnki.1004-7859.2017.06.010LU Shuping, SONG Haiyang, YI Wei, et al. Knowledge-aided CFAR algorithm based on radar knowledge base[J]. Modern Radar, 2017, 39(6): 46–49. doi: 10.16592/j.cnki.1004-7859.2017.06.010 [15] 刘红亮, 周生华, 刘宏伟, 等. 一种航迹恒虚警的目标检测跟踪一体化算法[J]. 电子与信息学报, 2016, 38(5): 1072–1078. doi: 10.11999/JEIT150638LIU Hongliang, ZHOU Shenghua, LIU Hongwei, et al. An integrated target detection and tracking algorithm with constant track false alarm rate[J]. Journal of Electronics &Information Technology, 2016, 38(5): 1072–1078. doi: 10.11999/JEIT150638 [16] 鲁瑞莲. 基于信息辅助的雷达检测跟踪一体化方法研究[D]. [硕士论文], 西安电子科技大学, 2018.LU Ruilian. Study of information aided radar detection and tracking coprocessing[D]. [Master dissertation], Xidian University, 2018. [17] CAI Jiajia, ZHOU Hao, HUANG Weimin, et al. Ship detection and direction finding based on time-frequency analysis for compact HF radar[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(1): 72–76. doi: 10.1109/LGRS.2020.2967387 [18] 梁建. 高频地波雷达目标二维CFAR检测及软件实现[D]. [硕士论文], 中国海洋大学, 2014.LIANG Jian. Target CFAR detection method and software implementation with two-dimension data for HFSWR[D]. [Master dissertation], Ocean University of China, 2014. [19] GOLDMAN H. Performance of the excision CFAR detector in the presence of interferers[J]. IEE Proceedings F (Radar and Signal Processing), 1990, 137(3): 163–171. doi: 10.1049/ip-f-2.1990.0024 [20] BORDONARO S, WILLETT P, and BAR-SHALOM Y. Decorrelated unbiased converted measurement Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1431–1444. doi: 10.1109/TAES.2014.120563 -






 下载:
下载:




 下载:
下载:
