基于完美二叉树通信拓扑的拜占庭容错共识算法

李淑芝; 熊伟志; 邓小鸿; 王智强; 刘惠文

doi:10.11999/JEIT220798

基于完美二叉树通信拓扑的拜占庭容错共识算法

doi: 10.11999/JEIT220798

李淑芝¹,
熊伟志¹,
邓小鸿^{2, 3, ,},
王智强¹,
刘惠文²

1.
江西理工大学信息工程学院赣州 341000
2.
赣南科技学院电子信息工程学院赣州 341000
3.
赣州市云计算与大数据重点实验室赣州 341000

基金项目: 国家自然科学基金(61762046, 62166019)，江西省自然科学基金(2020BABL202032), 江西省教育厅科研项目(GJJ218506, GJJ209412)

详细信息

作者简介:
李淑芝：女，硕士，教授，研究方向为软件工程、信息隐藏

熊伟志：男，硕士生，研究方向为区块链

邓小鸿：男，博士，副教授，研究方向为网络信息安全、区块链

王智强：男，硕士生，研究方向为区块链

刘惠文：女，硕士，讲师，研究方向为区块链及其应用

通讯作者:
邓小鸿　deng_xh@jxust.edu.cn

中图分类号: TN915; TP309
计量
- 文章访问数: 330
- HTML全文浏览量: 214
- PDF下载量: 78
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-16
- 修回日期: 2022-12-07
- 网络出版日期: 2022-12-09
- 刊出日期: 2023-07-10

Byzantine Fault-Tolerance Consensus Algorithm Based on Perfect Binary Tree Communication

1.
College of Information Science, Jiangxi University of Science and Technology, Ganzhou 341000, China
2.
School of Electronics and Information Engineering, Gannan University of Science and Technology, Ganzhou 341000, China
3.
Key Laboratory of Cloud Computing and Big Data, Ganzhou 341000, China

Funds: The National Natural Science Foundation of China (61762046, 62166019), The Natural Science Foundation of Jiangxi Province (2020BABL202032), The Scientific Research Project of Education Department of Jiangxi Province (GJJ218506, GJJ209412)

摘要

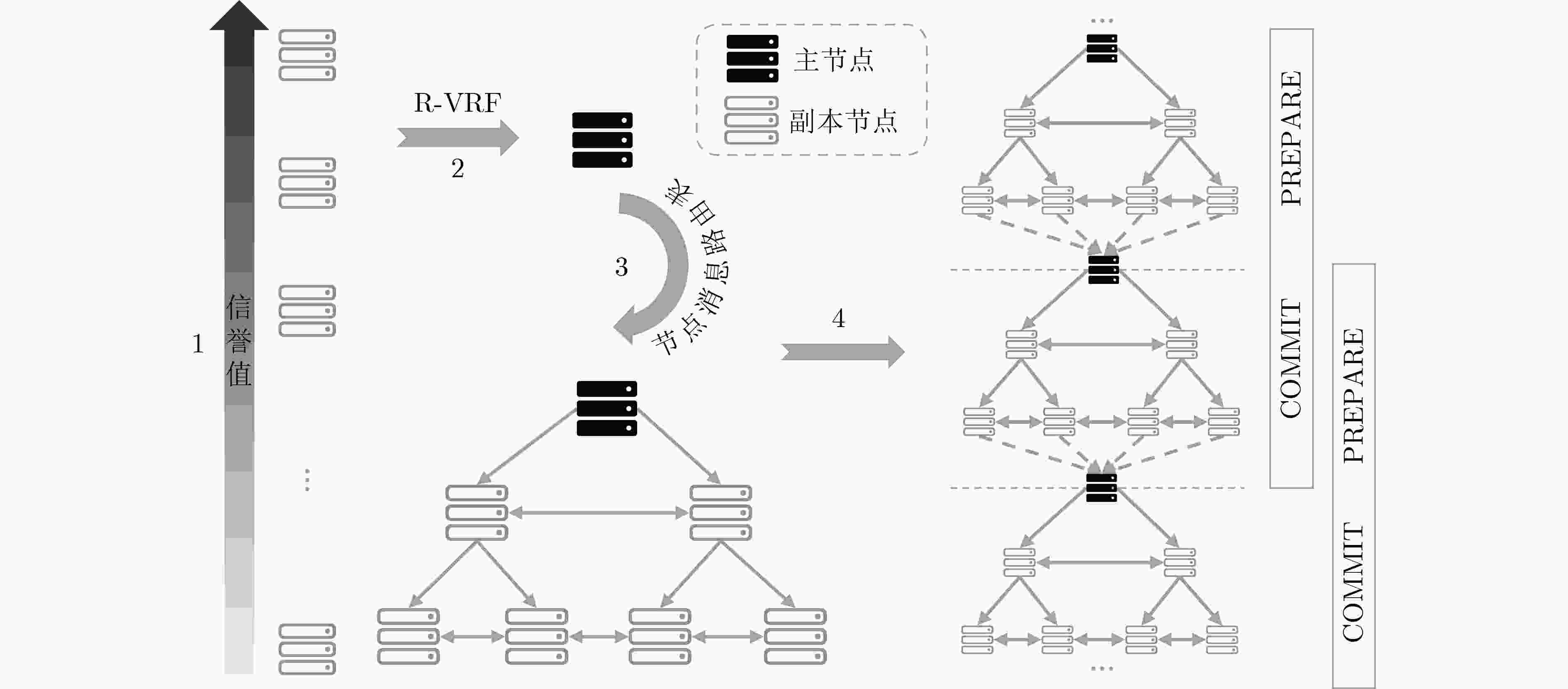
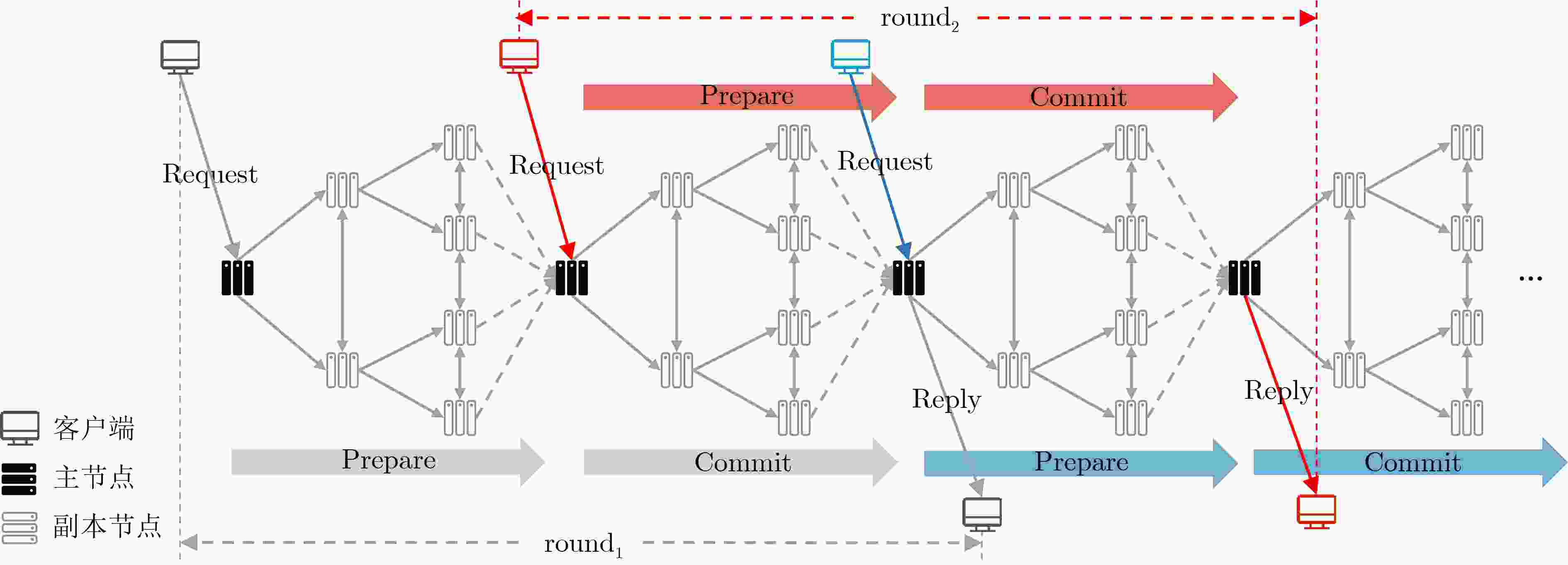
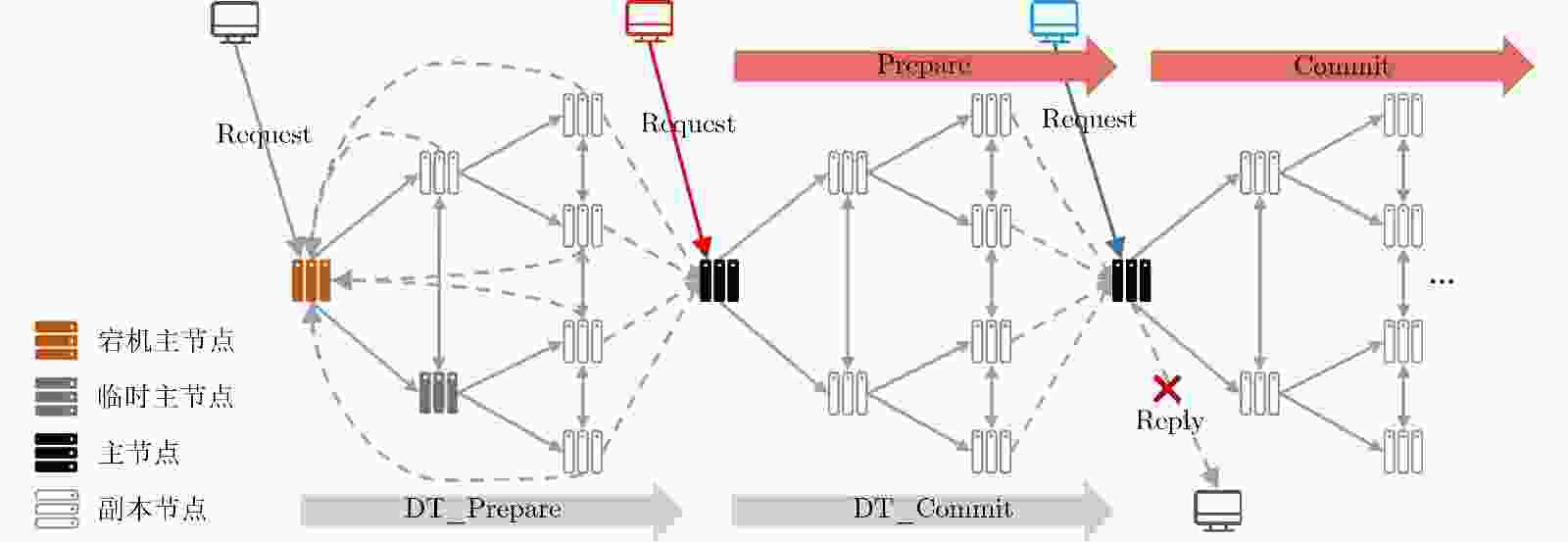
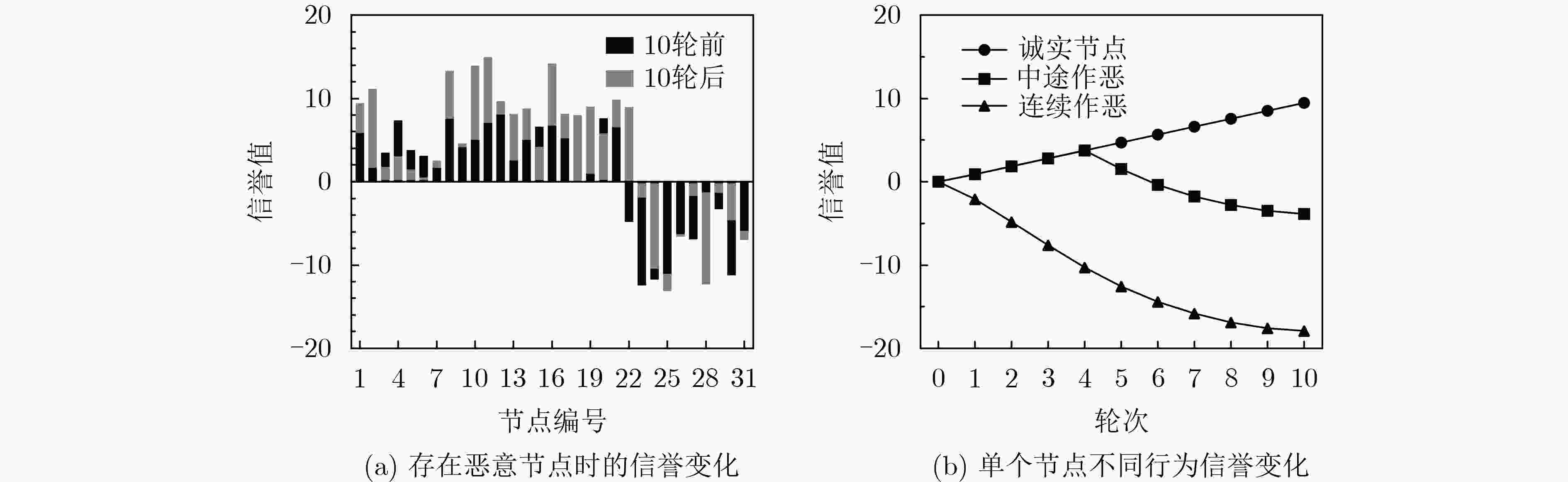
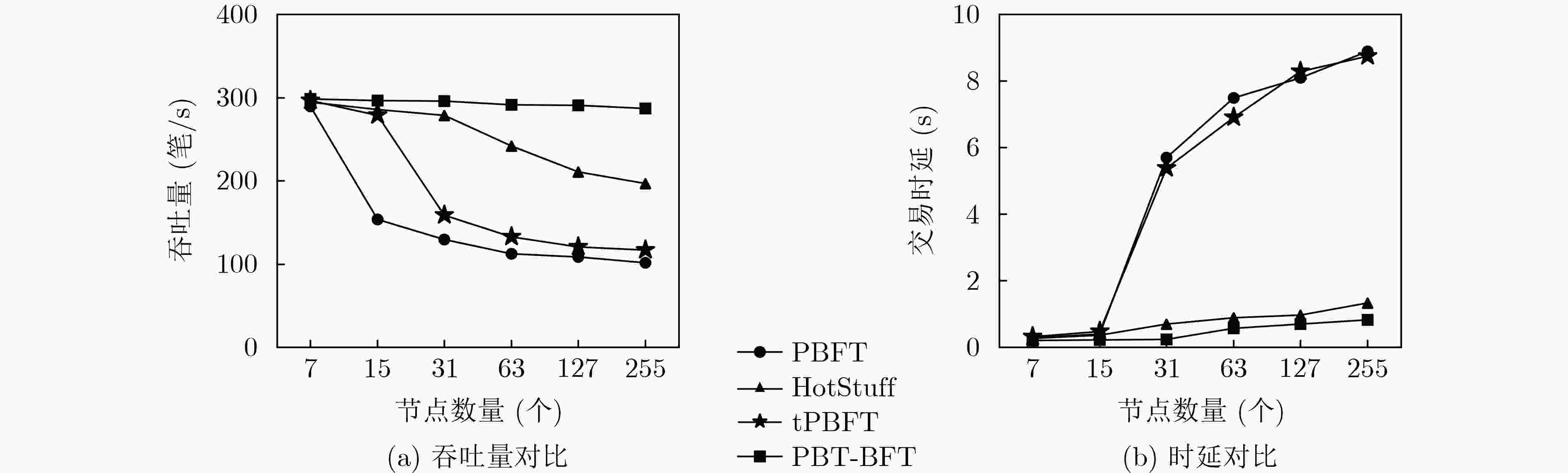
摘要: 针对实用拜占庭容错(PBFT)算法中主节点可预测、通信复杂度高和作恶节点缺少惩罚机制的问题，该文提出一种基于完美二叉树通信拓扑的联盟链拜占庭容错算法(PBT-BFT)。首先设计了信誉评估模型对节点的行为进行评估，同时提出基于信誉的可验证随机函数(R-VRF)，使得随机抽取概率与信誉值呈正相关，保证了拥有不同信誉值的节点抽签的公平性和随机性。然后，设计了完美二叉树通信拓扑，将通信复杂度降低至线性复杂度，同时提出轮换主节点和流水线工作机制，提高了共识效率。实验结果表明，与PBFT相比，平均吞吐量提高了121.6%，平均时延降低了73.8%，能够很好地适用于大规模网络节点的联盟链。
- 完美二叉树 /
- 通信拓扑 /
- 共识机制 /
- 拜占庭容错
Abstract: Considering the problems of a predictable primary node, high communication complexity, and lack of punishment mechanism for malicious nodes in Practical Byzantine Fault Tolerance (PBFT) algorithm, a consortium chain Byzantine Fault-Tolerant algorithm based on Perfect Binary Tree communication topology(PBT-BFT) is proposed. In PBT-BFT, a reputation evaluation model is designed to evaluate the behavior of nodes. At the same time, a Reputation-based Verifiable Random Function (R-VRF) is proposed, which makes the probability of random extraction positively correlated with the reputation value, and ensures the fairness and randomness of the lottery for nodes with different reputation values. Then, a perfect binary tree communication topology is designed to reduce the communication complexity to linear complexity, and a rotating primary node and Pipelining are proposed to improve the consensus efficiency. The experimental results show that compared with PBFT, the average throughput is increased by 121.6%, and the average delay is reduced by 73.8%, which can be well applied to the consortium chain of large-scale network nodes.
- Perfect binary tree /
- Communication topology /
- Consensus mechanism /
- Byzantine fault tolerance

HTML全文

图 1 PBT-BFT共识算法模型

下载: 全尺寸图片幻灯片

图 2 完美二叉树通信拓扑的构建

下载: 全尺寸图片幻灯片

图 3 共识流程图

下载: 全尺寸图片幻灯片

图 4 主节点宕机共识流程

下载: 全尺寸图片幻灯片

图 5 信誉评估效果

下载: 全尺寸图片幻灯片

图 6 主节点信誉分布图

下载: 全尺寸图片幻灯片

图 7 吞吐量、时延对比

下载: 全尺寸图片幻灯片

图 8 主节点连续切换时吞吐量对比

下载: 全尺寸图片幻灯片

表 1 信誉评估指标

1级指标	2级指标	符号表示
节点贡献度 $C_r^i$	转发消息数	${\text{Info}}_r^i$
	最大转发消息数	${\text{MaxInfo}}_r^i$
	创建有效区块	$B_r^i$
节点作恶度 $W_r^i$	出现宕机行为	${\text{Down}}_r^i$
	出现作恶行为	${\text{Bad}}_r^i$
	连续作恶系数	$\gamma $
	代价函数	${\text{Cost}}\left( x \right)$
历史信誉度 ${R_{{\text{old}}}}$	–	–

下载: 导出CSV

表 2 节点消息路由表

节点序号	邻接节点	父节点	信誉值
1	{2, 3}	–	0.5
2	{3, 4, 5}	1	0.6
3	{2, 6, 7}	1	0.5

下载: 导出CSV

参考文献(17)

[1]	NAKAMOTO S. Bitcoin: A peer-to-peer electronic cash system[EB/OL]. https://bitcoin.org/en/bitcoin-paper, 2022.
[2]	陈友荣, 章阳, 陈浩, 等. 面向车联网异构节点的区块链高效一致性共识算法研究[J]. 电子与信息学报, 2022, 44(1): 314–323. doi: 10.11999/JEIT201065 CHEN Yourong, ZHANG Yang, CHEN Hao, et al. Efficient consistency consensus algorithm of blockchain for heterogeneous nodes in the internet of vehicles[J]. Journal of Electronics &Information Technology, 2022, 44(1): 314–323. doi: 10.11999/JEIT201065
[3]	陈友荣, 陈浩, 韩蒙, 等. 基于信用等级划分的医疗数据安全共识算法[J]. 电子与信息学报, 2022, 44(1): 279–287. doi: 10.11999/JEIT200893 CHEN Yourong, CHEN Hao, HAN Meng, et al. Security consensus algorithm of medical data based on credit rating[J]. Journal of Electronics &Information Technology, 2022, 44(1): 279–287. doi: 10.11999/JEIT200893
[4]	邓小鸿, 王智强, 李娟, 等. 主流区块链共识算法对比研究[J]. 计算机应用研究, 2022, 39(1): 1–8. doi: 10.19734/j.issn.1001-3695.2021.06.0210 DENG Xiaohong, WANG Zhiqiang, LI Juan, et al. Comparative research on mainstream blockchain consensus algorithms[J]. Application Research of Computers, 2022, 39(1): 1–8. doi: 10.19734/j.issn.1001-3695.2021.06.0210
[5]	CASTRO M and LISKOV B. Practical Byzantine fault tolerance[C]. The Third Symposium on Operating Systems Design and Implementation, New Orleans, USA, 1999: 173–186.
[6]	黄冬艳, 李浪, 陈斌, 等. RBFT: 基于Raft集群的拜占庭容错共识机制[J]. 通信学报, 2021, 42(3): 209–219. doi: 10.11959/j.issn.1000-436x.2021043 HUANG Dongyan, LI Lang, CHEN Bin, et al. RBFT: A new Byzantine fault-tolerant consensus mechanism based on Raft cluster[J]. Journal on Communications, 2021, 42(3): 209–219. doi: 10.11959/j.issn.1000-436x.2021043
[7]	赖英旭, 薄尊旭, 刘静. 基于改进PBFT算法防御区块链中Sybil攻击的研究[J]. 通信学报, 2020, 41(9): 104–117. doi: 10.11959/j.issn.1000-436x.2020170 LAI Yingxu, BO Zunxu, and LIU Jing. Research on Sybil attack in defense blockchain based on improved PBFT algorithm[J]. Journal on Communications, 2020, 41(9): 104–117. doi: 10.11959/j.issn.1000-436x.2020170
[8]	王日宏, 袁杉杉, 徐泉清, 等. 基于时间权重值的共识算法研究[J]. 计算机应用研究, 2021, 38(11): 3243–3248. doi: 10.19734/j.issn.1001-3695.2021.03.0097 WANG Rihong, YUAN Shanshan, XU Quanqing, et al. Consensus algorithm based on time weight value[J]. Application Research of Computers, 2021, 38(11): 3243–3248. doi: 10.19734/j.issn.1001-3695.2021.03.0097
[9]	ZHAN Yu, WANG Baocang, LU Rongxing, et al. DRBFT: Delegated randomization Byzantine fault tolerance consensus protocol for blockchains[J]. Information Sciences, 2021, 559: 8–21. doi: 10.1016/j.ins.2020.12.077
[10]	LI Y X, QIAO Liang, and LV Zhihan. An optimized byzantine fault tolerance algorithm for consortium blockchain[J]. Peer-to-Peer Networking and Applications, 2021, 14(5): 2826–2839. doi: 10.1007/s12083-021-01103-8
[11]	CHEN Yineng, LI Ming, ZHU Xinghui, et al. An improved algorithm for practical byzantine fault tolerance to large-scale consortium chain[J]. Information Processing & Management, 2022, 59(2): 102884. doi: 10.1016/j.ipm.2022.102884
[12]	TANG Song, WANG Zhiqiang, JIANG Jian, et al. Improved PBFT algorithm for high-frequency trading scenarios of alliance blockchain[J]. Scientific Reports, 2022, 12(1): 4426. doi: 10.1038/s41598-022-08587-1
[13]	MICALI S, RABIN M, and VADHAN S. Verifiable random functions[C]. The 40th Annual Symposium on Foundations of Computer Science, New York, USA, 1999: 120–130.
[14]	GILAD Y, HEMO R, MICALI S, et al. Algorand: Scaling byzantine agreements for cryptocurrencies[C]. The 26th Symposium on Operating Systems Principles, Shanghai, China, 2017: 51–68.
[15]	GOLDBERG S, REYZIN L, PAPADOPOULOS D, et al. Verifiable random functions (VRFs)[EB/OL], https://datatracker.ietf.org/doc/draft-irtf-cfrg-vrf/11/, 2022.
[16]	ALQAHTANI S and DEMIRBAS M. Bottlenecks in blockchain consensus protocols[C]. 2021 IEEE International Conference on Omni-Layer Intelligent Systems (COINS), Barcelona, Spain, 2021: 1–8.
[17]	YIN Maofan, MALKHI D, REITER M K, et al. HotStuff: BFT consensus with linearity and responsiveness[C]. The 2019 ACM Symposium on Principles of Distributed Computing, Toronto, Canada, 2019: 347–356.