A Highly Robust Underwater 3D Localization Algorithm Based on Iterative Least Square
-
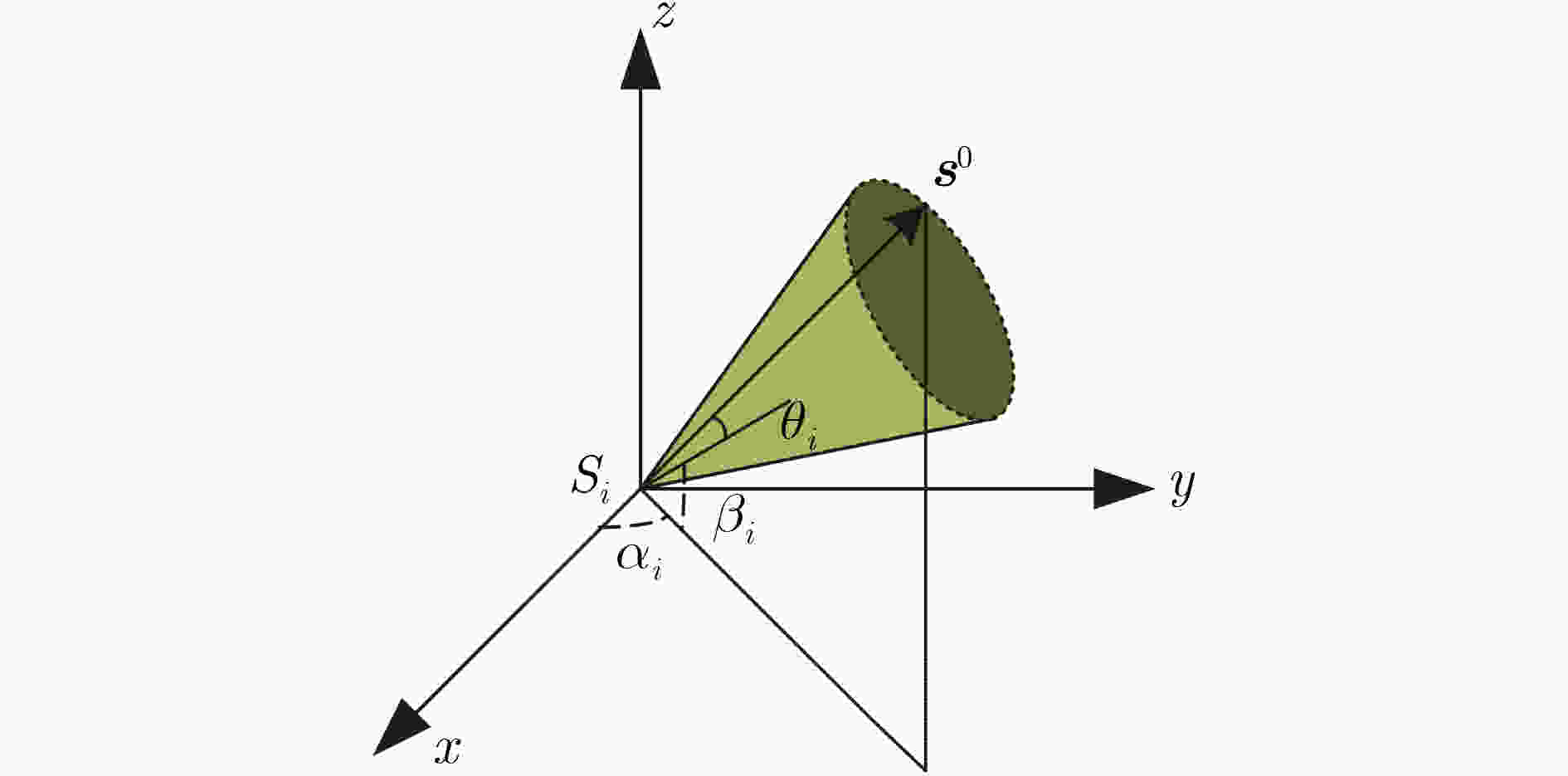
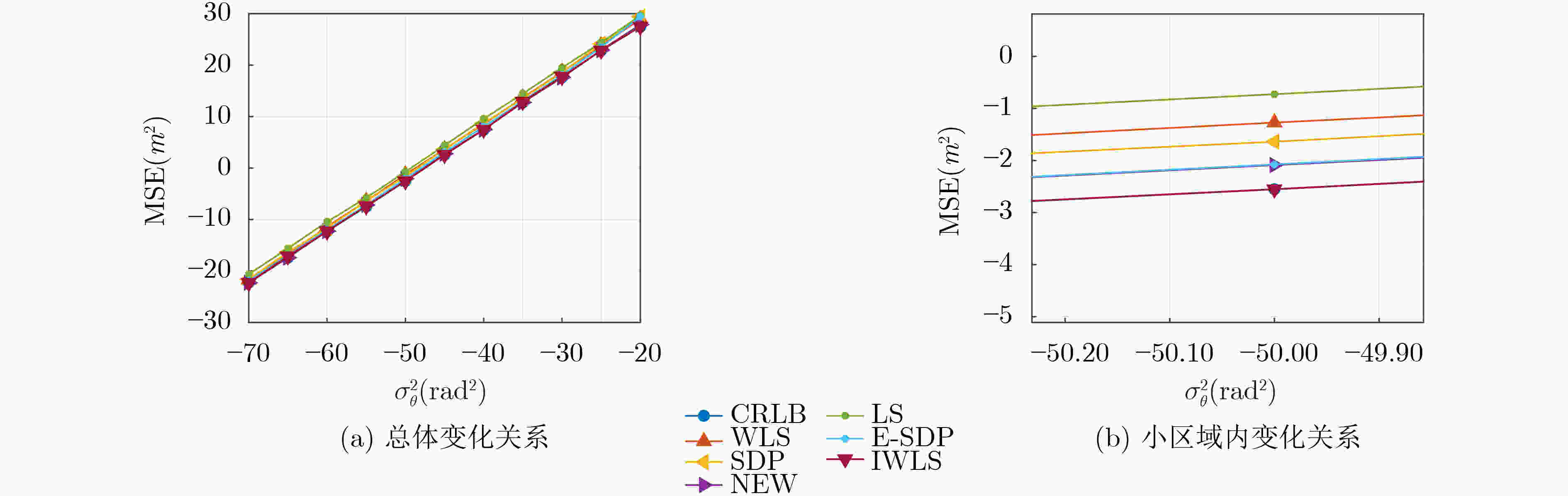
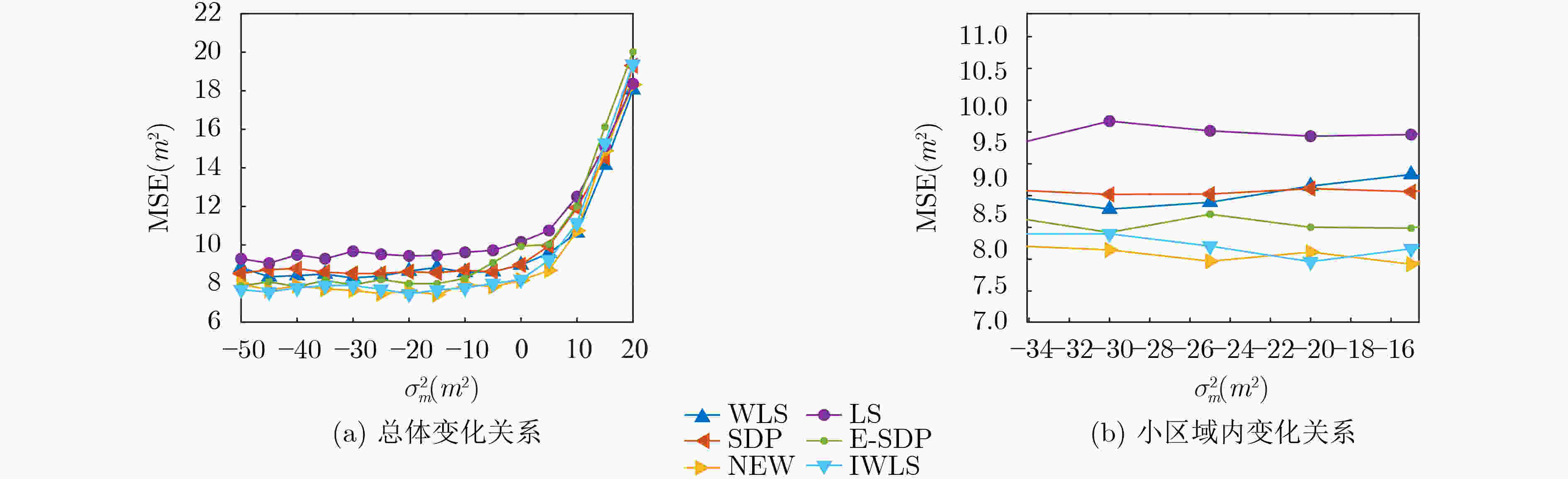
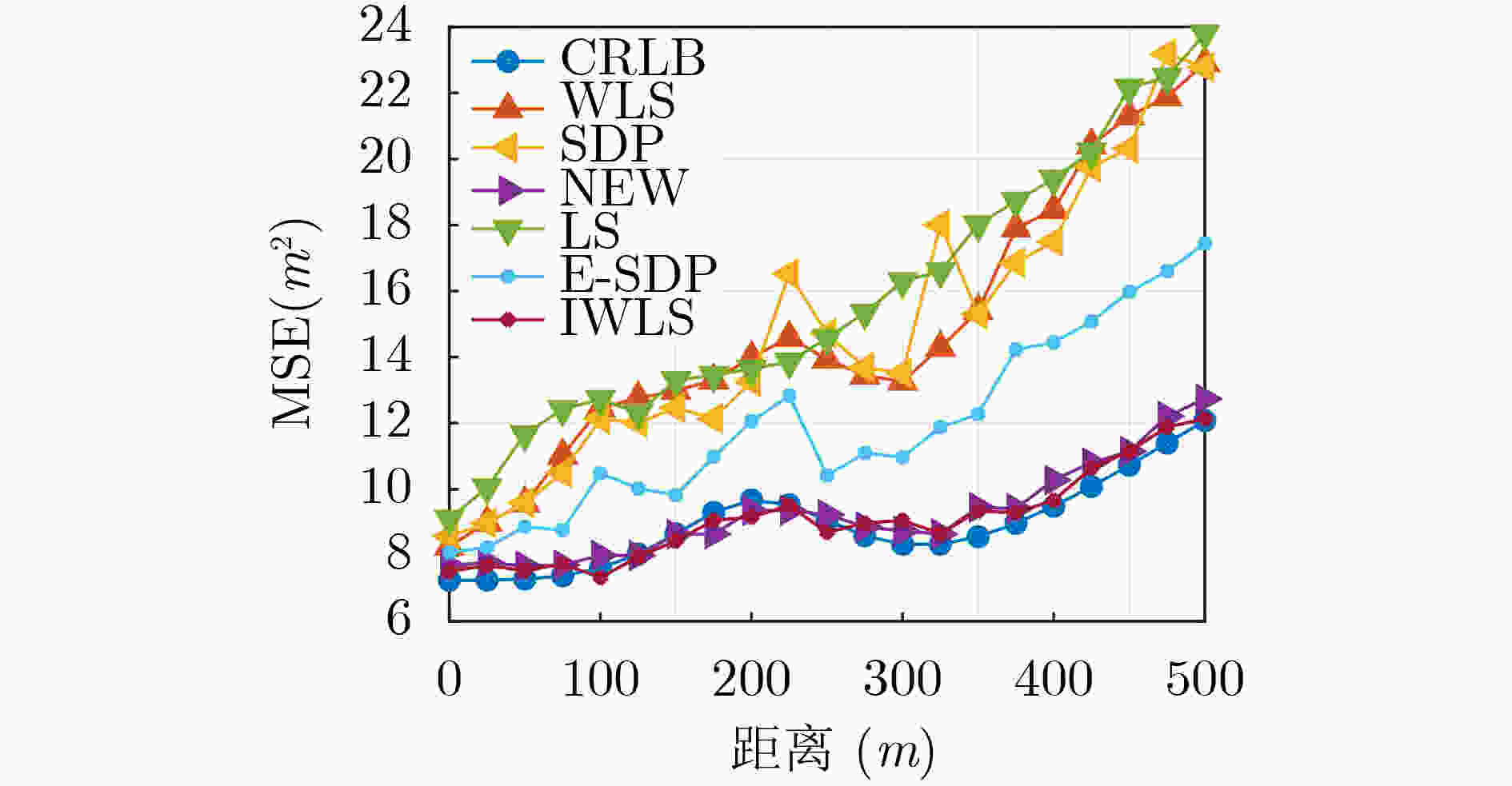
摘要: 为解决基于空间角信息水下3维定位中,闭式解算法中定位性能无法达到克拉默-拉奥界(CRLB)和牛顿迭代算法初始值选取问题,该文利用一种基于迭代最小二乘的高鲁棒性算法修正闭式解的残差项与选取迭代算法的初始值。利用伪线性加权最小二乘算法得到闭式解作为正则化修正迭代法的初始值,将迭代结果修正闭式解算法的残差项,通过迭代最小二乘法的交替运算,得到稳定精确的解。通过仿真验证了基于迭代最小二乘算法的高鲁棒性,消除伪线性加权最小二乘算法中残差项选取的不利影响,解决了迭代法初始值选取问题,得到与收敛情况下迭代法相近的定位性能。Abstract: In order to solve the problem that the positioning performance of the closed solution algorithm can not reach the Cramer Rao Lower Bound (CRLB) and the initial value selection of Newton iterative algorithm in the underwater three-dimensional positioning based on spatial angle information, a highly robust algorithm based on iterative least squares is used to correct the residual term of the closed form solution and select the initial value of the iterative algorithm. The pseudo linear Weighted Least Squares (WLS) algorithm is used to obtain the closed form solution as the initial value of the regularization modified iterative method. The iterative result is used to modify the residual term of the closed form solution algorithm. Through the alternating operation of the iterative least squares method, a stable and accurate solution is obtained. Through simulation, the high robustness of the iterative least squares algorithm is verified, the adverse effect of the selection of the residual term in the pseudo linear weighted least squares algorithm is eliminated, the problem of selecting the initial value of the iterative method is solved, and the positioning performance similar to that of the iterative method in the case of convergence is obtained.
-
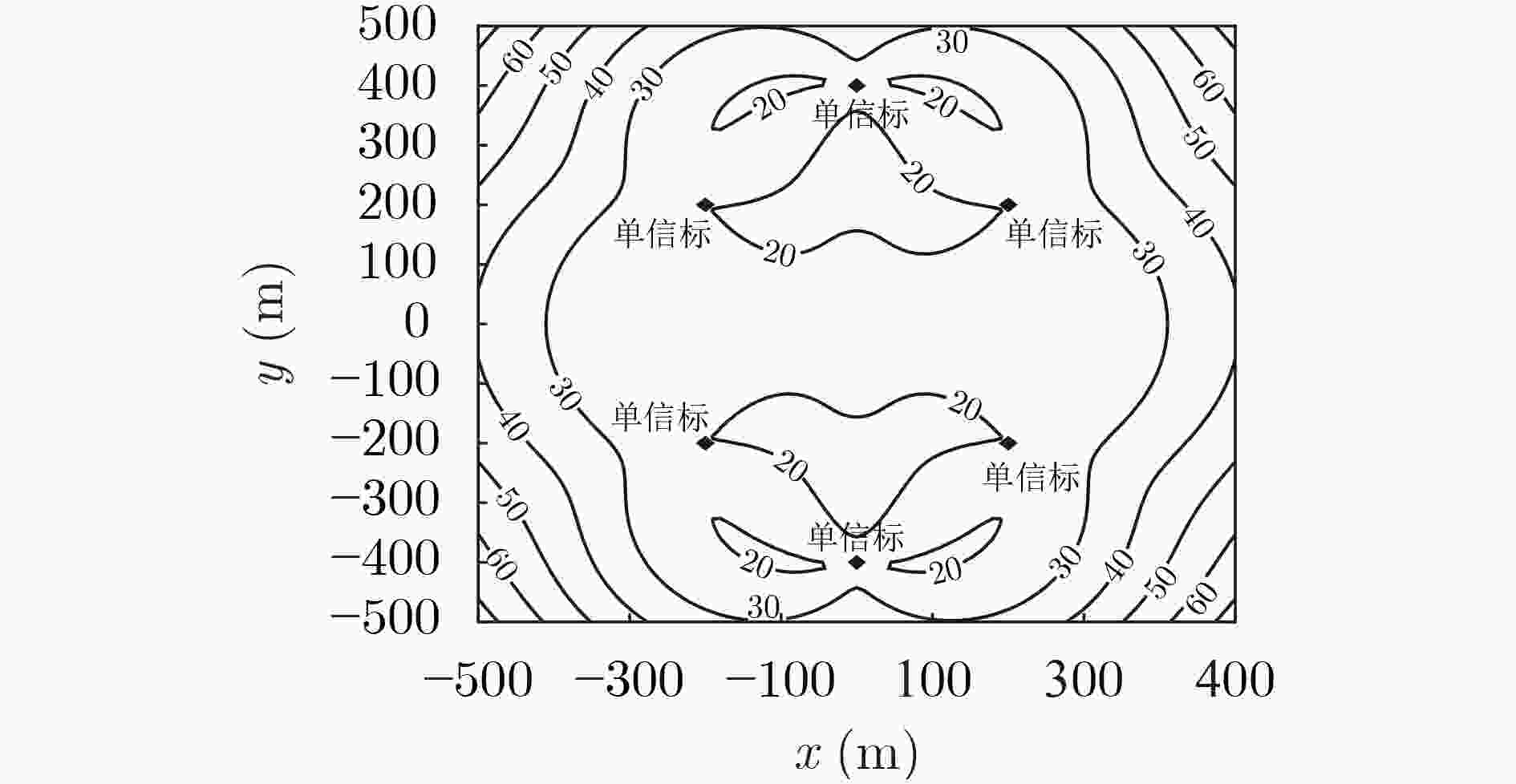
表 1 仿真布阵
浮标序号 1 2 3 4 5 6 X (m) 0 –200 200 –200 0 200 Y (m) 400 200 200 –200 –400 –200 线阵角度( rad) ${{\pi} \mathord{\left/ {\vphantom {{\pi} 3}} \right. } 3}$ ${{\pi} \mathord{\left/ {\vphantom {{\pi} {\text{3}}}} \right. } {\text{3}}}$ ${{\pi} \mathord{\left/ {\vphantom {{\pi} {\text{3}}}} \right. } {\text{3}}}$ ${{\pi} \mathord{\left/ {\vphantom {{\pi} {\text{3}}}} \right. } {\text{3}}}$ ${{\pi} \mathord{\left/ {\vphantom {{\pi} {\text{3}}}} \right. } {\text{3}}}$ ${{\pi} \mathord{\left/ {\vphantom {{\pi} {\text{3}}}} \right. } {\text{3}}}$ -
[1] 张同伟, 王向鑫, 唐嘉陵, 等. 深海超短基线定位系统现状及展望[J]. 舰船电子工程, 2018, 38(10): 1–6. doi: 10.3969/j.issn.1672-9730.2018.10.001ZHANG Tongwei, WANG Xiangxin, TANG Jialing, et al. Technical status and development trend of long range USBL[J]. Ship Electronic Engineering, 2018, 38(10): 1–6. doi: 10.3969/j.issn.1672-9730.2018.10.001 [2] GUO Bo, MA Jianye, and GUAN Juhua. Performance comparison among the various underwater acousitic positioning algorithms[C]. Proceedings of 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 2021: 92–95. [3] SHENG Huantang, WU Wenrong, HSIAO W H, et al. Joint channel and AoA estimation in OFDM systems: One channel tap with multiple AoAs problem[J]. IEEE Communications Letters, 2021, 25(7): 2245–2249. doi: 10.1109/LCOMM.2021.3070874 [4] ZHU Xiaodan, ZHU Weiqiang, and CHEN Zhuo. Direct localization based on motion analysis of single-station using TOA[C]. Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2018: 1823–1827. [5] ZHU Junjie, KOUDA E, HOU Pengcheng, et al. Indoor simultaneous TOA estimation of multiple users using leaky coaxial cable[C]. Proceedings of the 2022 IEEE 4th Global Conference on Life Sciences and Technologies (LifeTech), Osaka, Japan, 2022: 297–298. [6] WANG Lijuan, SU Dan, LIU Mei, et al. Modified zeroing neurodynamics models for range-based WSN localization from AOA and TDOA measurements[J]. IEEE Sensors Journal, 2022, 22(23): 13716–13726. doi: 10.1109/JSEN.2022.3177409 [7] PAN Jianghuai. Multi-station TDOA localization method based on tikhonov regularization[C]. Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi'an, China, 2022: 1903–1906. [8] 韩云峰, 李昭, 郑翠娥, 等. 一种基于长基线交汇的超短基线定位系统精度评价方法[J]. 物理学报, 2015, 64(9): 350–356. doi: 10.7498/aps.64.094301HAN Yunfeng, LI Zhao, ZHENG Cuie, et al. A precision evaluation metho d of USBL p ositioning systems based on LBL triangulationAn evaluation method of ultra short baseline positioning system accuracy based on long baseline intersection[J]. Acta Physica Sinica, 2015, 64(9): 350–356. doi: 10.7498/aps.64.094301 [9] 梁国龙, 张毅锋, 付进. 利用夹角几何关系的超短基线定位方法[J]. 哈尔滨工程大学学报, 2019, 40(8): 1474–1479. doi: 10.11990/jheu.201808081LIANG Guolong, ZHANG Yifeng, and FU Jin. Angle-based underwater source localization for USBLAngle-based underwater source localization for USBL[J]. Journal of Harbin Engineering University, 2019, 40(8): 1474–1479. doi: 10.11990/jheu.201808081 [10] ZHOU Yifan, WANG Yingmin, NIE Ruixin, et al. Optimal location method of spontaneous data fusion based on TDOA / AOA[C]. Proceedings of 2021 OES China Ocean Acoustics (COA), Harbin, China, 2021: 885–889. [11] HAO Kun, XUE Qixin, LI Cheng, et al. A hybrid localization algorithm based on doppler shift and AOA for an underwater mobile node[J]. IEEE Access, 2020, 8: 181662–181673. doi: 10.1109/ACCESS.2020.3028608 [12] 黄东华, 赵勇胜, 赵拥军, 等. 基于DOA-TDOA-FDOA的单站无源相干定位代数解[J]. 电子与信息学报, 2021, 43(3): 735–744. doi: 10.11999/JEIT200470HUANG Donghua, ZHAO Yongsheng, ZHAO Yongjun, et al. An algebraic solution for single-observer passive coherent location using DOA-TDOA-FDOA measurements[J]. Journal of Electronics &Information Technology, 2021, 43(3): 735–744. doi: 10.11999/JEIT200470 [13] 雍龙泉. 非线性方程牛顿迭代法研究进展[J]. 数学的实践与认识, 2021, 51(15): 240–249.YONG Longquan. Advances in newton's iterative methods for nonlinear equationResearch progress of newton iterative method for nonlinear equations[J]. Mathematics in Practice and Theory, 2021, 51(15): 240–249. [14] WANG Yue and HO K C. An asymptotically efficient estimator in closed-form for 3-D AOA localization using a sensor network[J]. IEEE Transactions on Wireless CommunicationsIEEE Trans Wireless Commun, 2015, 14(12): 6524–6535. doi: 10.1109/TWC.2015.2456057 [15] SUN Yimao, HO K C, and WAN Qun. Eigenspace solution for AOA localization in modified polar representation[J]. IEEE Transactions on Signal ProcessingIEEE Trans Signal Process, 2020, 68: 2256–2271. doi: 10.1109/TSP.2020.2981773 [16] ZOU Jifeng, SUN Yimao, and WAN Qun. A novel 3-D localization scheme using 1-D angle measurements[J]. IEEE Sensors Letters, 2020, 4(6): 1–4. doi: 10.1109/LSENS.2020.2992704 [17] ALAMDARI E, BEHNIA F, and AMIRI R. Conical localization from angle measurements: An approximate convex solution[J]. IEEE Sensors Letters, 2022, 6(5): 1–4. doi: 10.1109/LSENS.2022.3163186 -





 下载:
下载:



 下载:
下载:
