Identification of LOS Clusters in Power Angular Spectrum for Indoor Localization Compatible with Communication at Millimeter Band
-
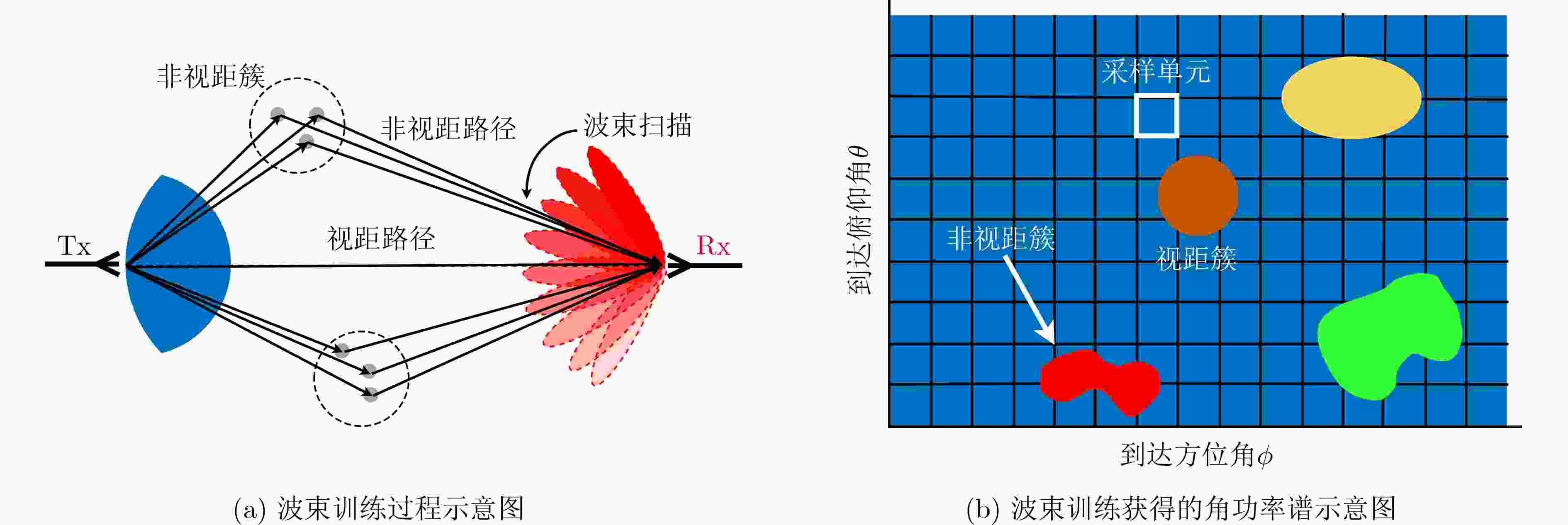
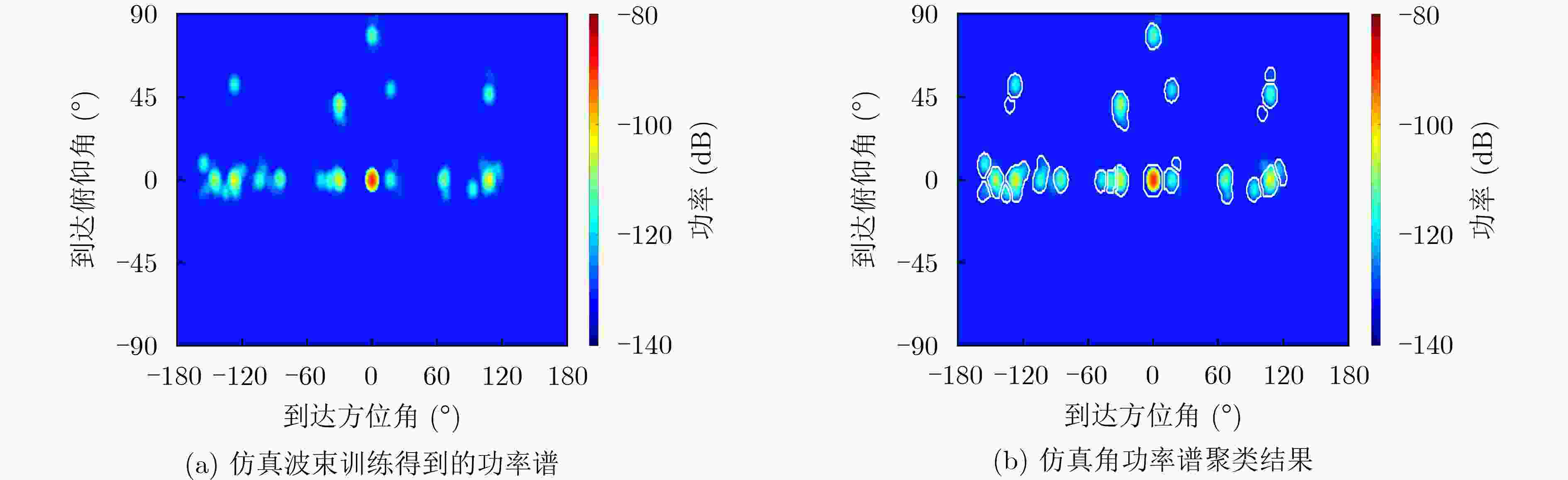
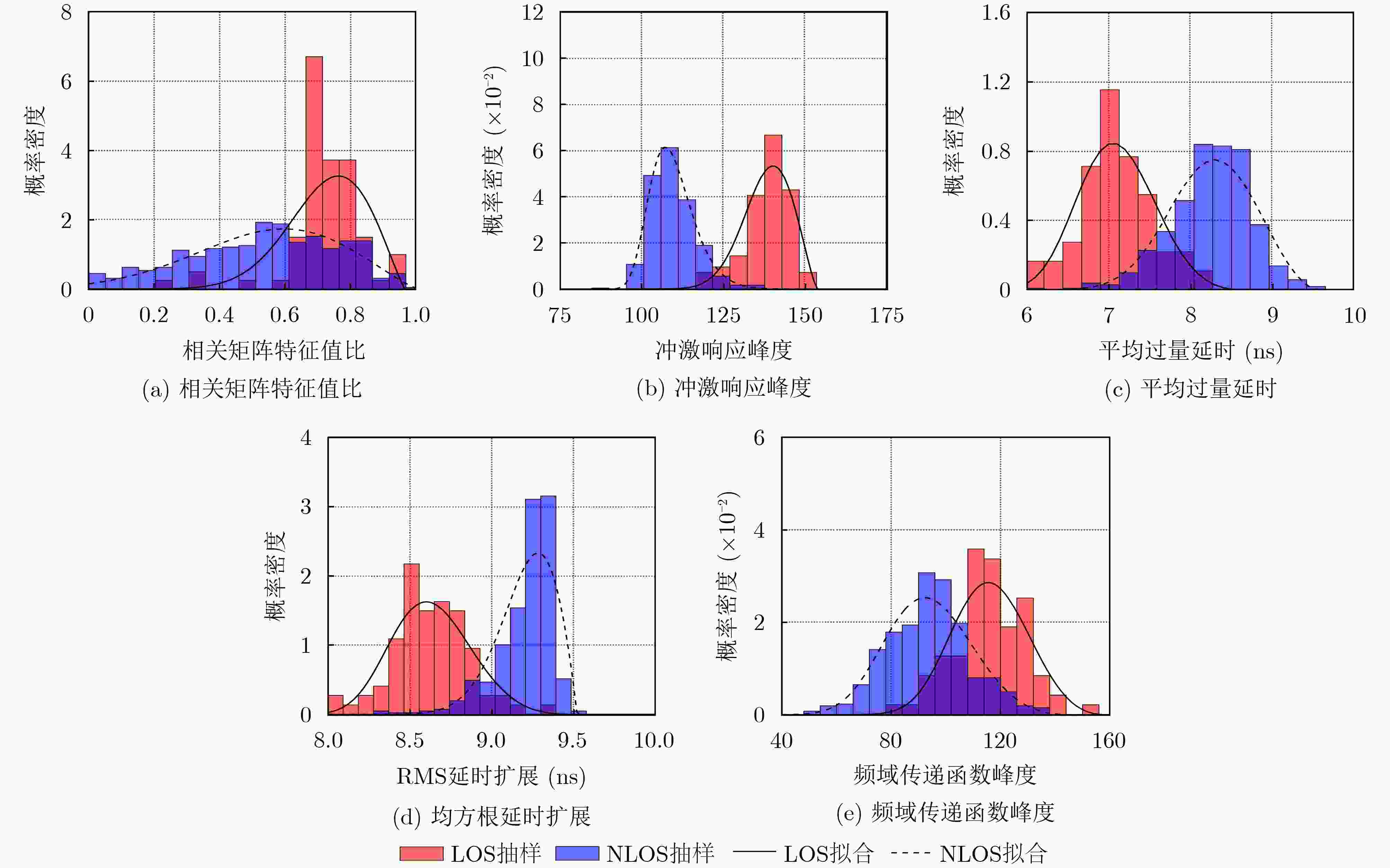
摘要: 该文提出一种在室内无线定位中识别毫米波视距传输(LoS)的方法,在室内毫米波无线通信的波束训练框架下,实现了信道角功率谱(PAS)中视距角度簇的识别。该方法通过分水岭算法,将角功率谱聚类成簇,进而采用最大似然比和人工神经网络分析角度簇内5个不同信道指标,即空间对称性、冲激响应和传递函数的信号峰度、平均过度延迟和均方根(RMS)延迟扩展。仿真结果中可观察到视距和非视距(NLOS)角功率谱簇之间差异明显,并以实验验证了该识别方法的有效性。Abstract: An identification method of Line-of-Sight (LOS) propagation for indoor localization at millimeter band is proposed in this paper. Based on beam training process, the proposed method identifies the LOS clusters in power angular spectrum. After clustering the Power Angular Spectrum (PAS), the statistical characteristics of five different channel metrics intra-clusters, namely the spatial-domain symmetry, kurtosis of impulse response and transfer function, mean excess delay, and Root Mean Square (RMS) delay spread, are analyzed using maximum likelihood ratio and artificial neural network. A noticeable difference between LOS and Non- Line-of-Sight (NLOS) clusters is observed, and validated with measurement.
-
表 1 识别视距传输簇的仿真错误率
检验方法 检验指标 第1类错误 第2类错误 最大似然比 相关矩阵特征值比 0.154 0.197 冲激响应峰度 0.040 0.125 频域传递函数峰度 0.152 0.671 平均过量延时 0.094 0.097 均方根延时扩展 0.242 0.447 联合指标 0.048 0.024 神经网络 联合指标 0.027 0.005 表 2 测量系统参数
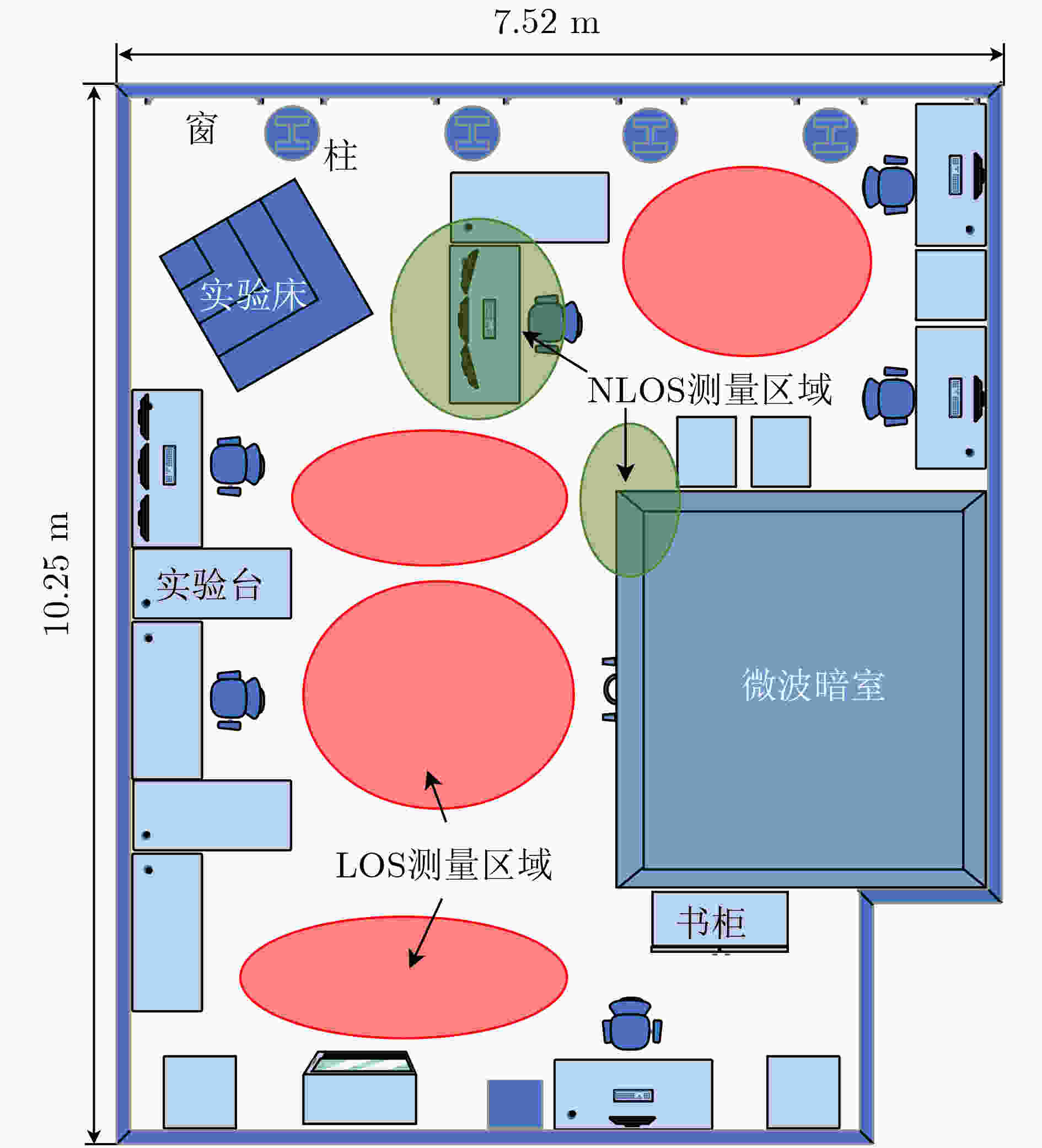
实验参数 参数值 带宽(GHz) 8.64 时间分辨率(ns) 0.12 频率采样点个数 752 频域分辨率(MHz) 11.5 发射功率(dBm) 4 Rx波束宽度(E/H面)(°) 10.1/13.1 Tx波束宽度(E/H面)(°) 360/60 Tx天线增益(dB) 2 Rx天线增益(dB) 24 方位向扫描范围(°) [–180, 180] 俯仰向扫描范围(°) [–45, 90] 空间扫描采样间隔(°) 5 表 3 识别视距传输簇的测量错误率
检验方法 检验指标 第1类错误 第2类错误 最大似然比 相关矩阵特征值比 0.1050 0.2418 冲激响应峰度 0.0200 0.0573 频域传递函数峰度 0.2598 0.1228 平均过量延时 0.1900 0.1111 均方根延时扩展 0.1750 0.1228 联合指标 0.1319 0.0183 神经网络 联合指标 0.0669 0.0408 -
[1] OBEIDAT H, SHUAIEB W, OBEIDAT O, et al. A review of indoor localization techniques and wireless technologies[J]. Wireless Personal Communications, 2021, 119(1): 289–327. doi: 10.1007/s11277-021-08209-5 [2] RIDOLFI M, KAYA A, BERKVENS R, et al. Self-calibration and collaborative localization for UWB positioning systems: A survey and future research directions[J]. ACM Computing Surveys, 2022, 54(4): 88. doi: 10.1145/3448303 [3] IEEE. 802.11ad-2012 Wireless LAN medium access control (MAC) and physical layer (PHY) specifications amendment 3: Enhancements for very high throughput in the 60 GHz band[S]. New York: IEEE, 2012. [4] IEEE. 802.11ay-2021 Wireless LAN medium access control (MAC) and physical layer (PHY) specifications amendment 2: Enhanced throughput for operation in license-exempt bands above 45 GHz[S]. New York: IEEE, 2021. [5] International Telecommunication Union. Recommendation P. 676-6: Attenuation by atmospheric gases[R]. ITU, 2005. [6] JAFARI A, MAVRIDIS T, PETRILLO L, et al. UWB interferometry TDOA estimation for 60-GHz OFDM communication systems[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1438–1441. doi: 10.1109/LAWP.2015.2512327 [7] DE LIMA C, BELOT D, BERKVENS R, et al. Convergent communication, sensing and localization in 6G systems: An overview of technologies, opportunities and challenges[J]. IEEE Access, 2021, 9: 26902–26925. doi: 10.1109/ACCESS.2021.3053486 [8] XIAO Zhiqiang and ZENG Yong. An overview on integrated localization and communication towards 6G[J]. Science China Information Sciences, 2022, 65(3): 131301. doi: 10.1007/s11432-020-3218-8 [9] YANG Tian, CABANI A, and CHAFOUK H. A survey of recent indoor localization scenarios and methodologies[J]. Sensors, 2021, 21(23): 8086. doi: 10.3390/s21238086 [10] GUVENC I, CHONG C C, and WATANABE F. NLOS identification and mitigation for UWB localization systems[C]. IEEE Wireless Communications & Networking Conference, Hong Kong, China, 2007: 1571–1576. [11] MARANÒ S, GIFFORD W M, WYMEERSCH H, et al. NLOS identification and mitigation for localization based on UWB experimental data[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(7): 1026–1035. doi: 10.1109/JSAC.2010.100907 [12] SHAFI M, ZHANG Jianhua, TATARIA H, et al. Microwave vs. millimeter-wave propagation channels: Key differences and impact on 5G cellular systems[J]. IEEE Communications Magazine, 2018, 56(12): 14–20. doi: 10.1109/MCOM.2018.1800255 [13] SUN Shu, RAPPAPORT T S, HEATH R W, et al. Mimo for millimeter-wave wireless communications: Beamforming, spatial multiplexing, or both?[J]. IEEE Communications Magazine, 2014, 52(12): 110–121. doi: 10.1109/MCOM.2014.6979962 [14] LIANG Xiaolin, JIN Yiheng, ZHANG Hao, et al. NLOS identification and machine learning methods for predicting the outcome of 60GHz ranging system[J]. Chinese Journal of Electronics, 2018, 27(1): 175–182. doi: 10.1049/cje.2017.11.003 [15] MALTSEV A. 802.11-09/0334r8 Channel models for 60 GHz WLAN systems[S]. New York: IEEE, 2010. [16] MALTSEV A, MASLENNIKOV R, SEVASTYANOV A, et al. Experimental investigations of 60 GHz WLAN systems in office environment[J]. IEEE Journal on Selected Areas in Communications, 2009, 27(8): 1488–1499. doi: 10.1109/JSAC.2009.091018 [17] LYU Pengfei, BENLARBI-DELAÏ A, REN Zhuoxiang, et al. Angular clustering of millimeter-wave propagation channels with watershed transformation[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(2): 1279–1290. doi: 10.1109/TAP.2021.3119051 -





 下载:
下载:




 下载:
下载:
