Outage Performance of Commensal Symbiotic Radio Based on Energy Harvesting
-
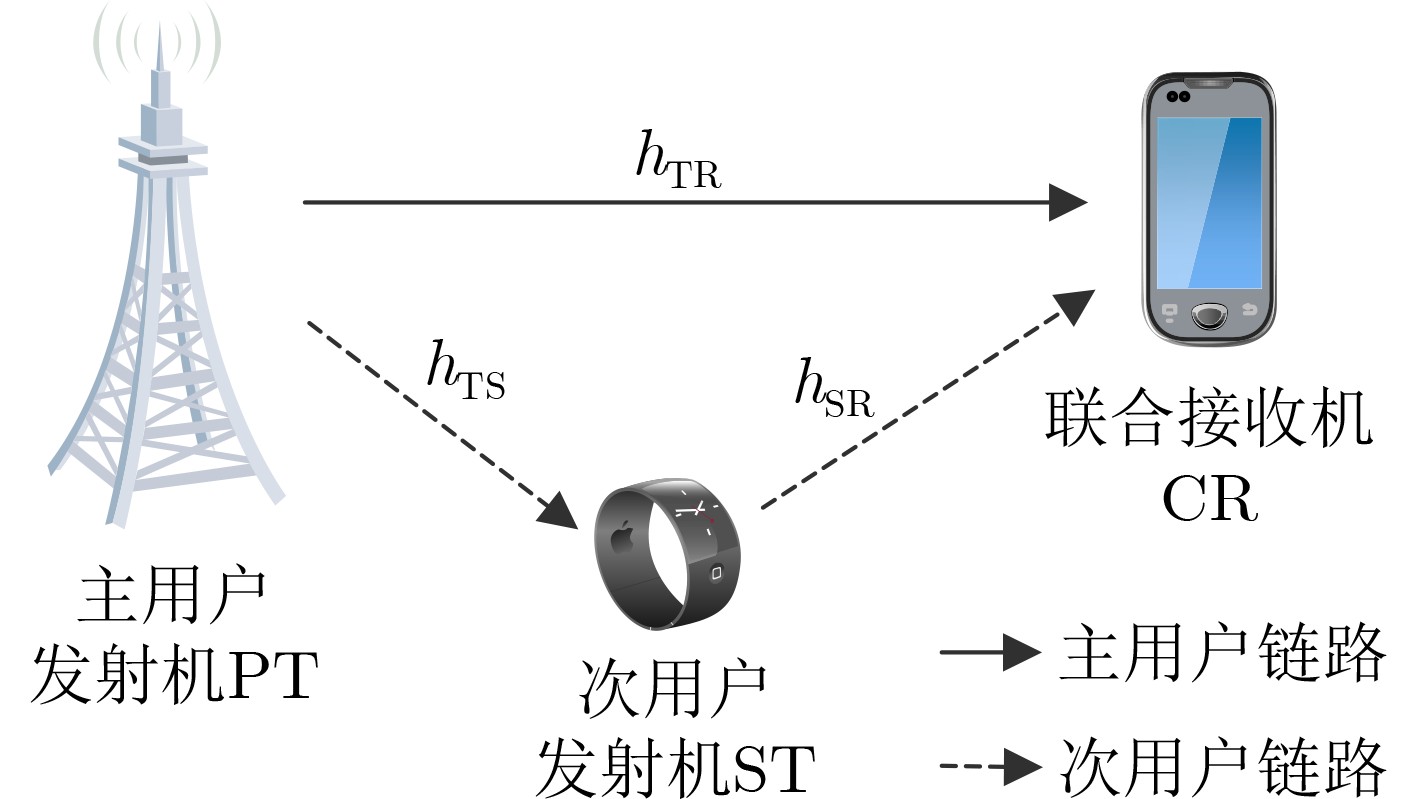
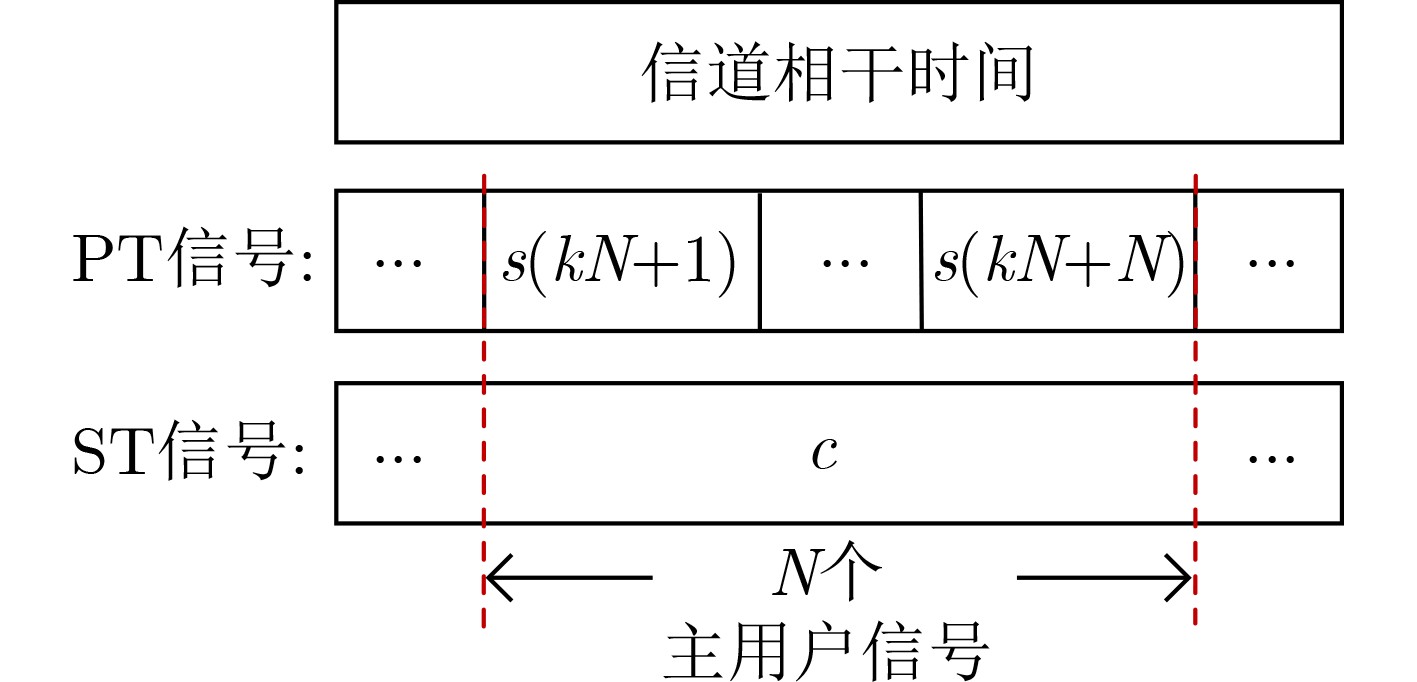
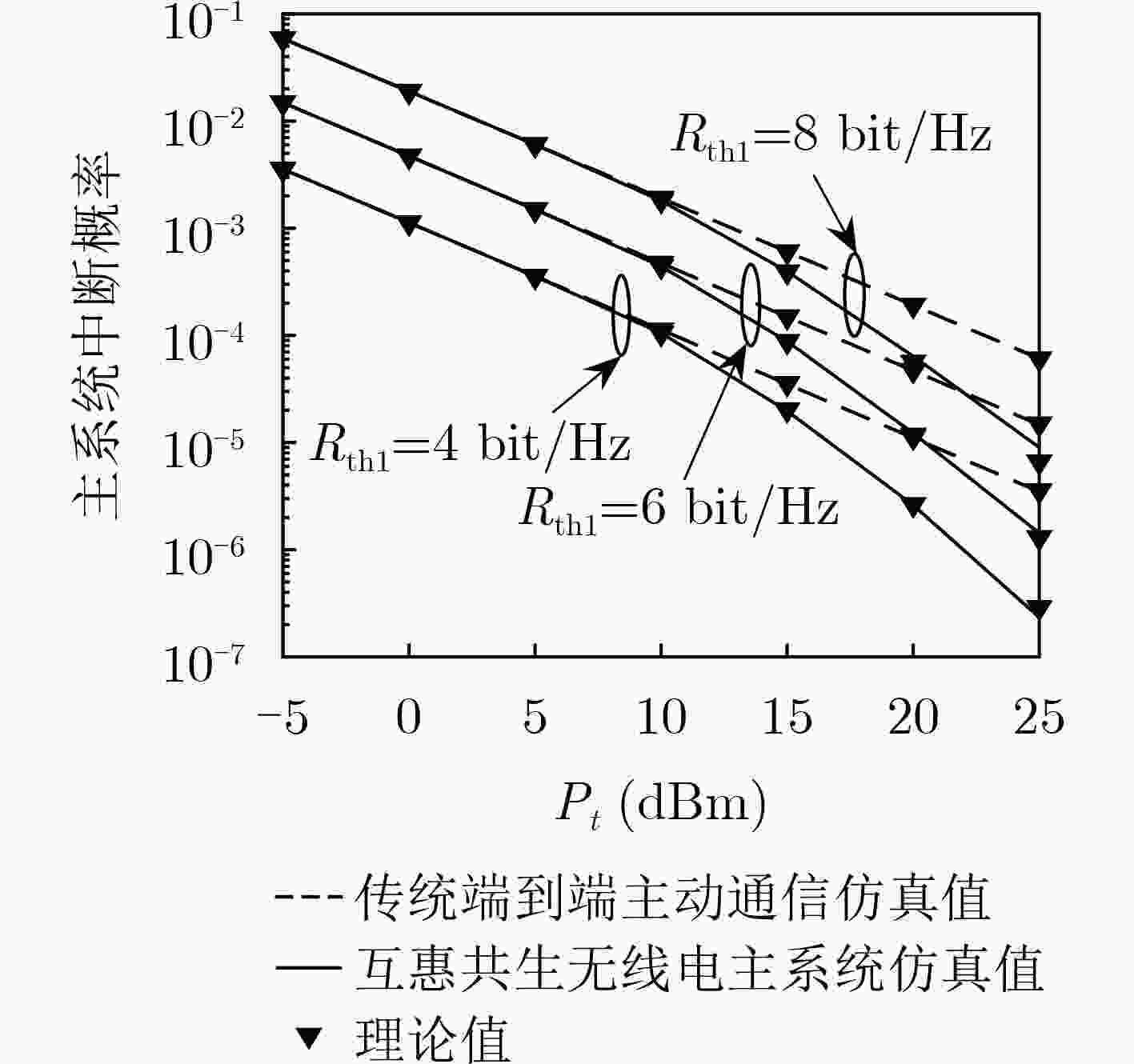
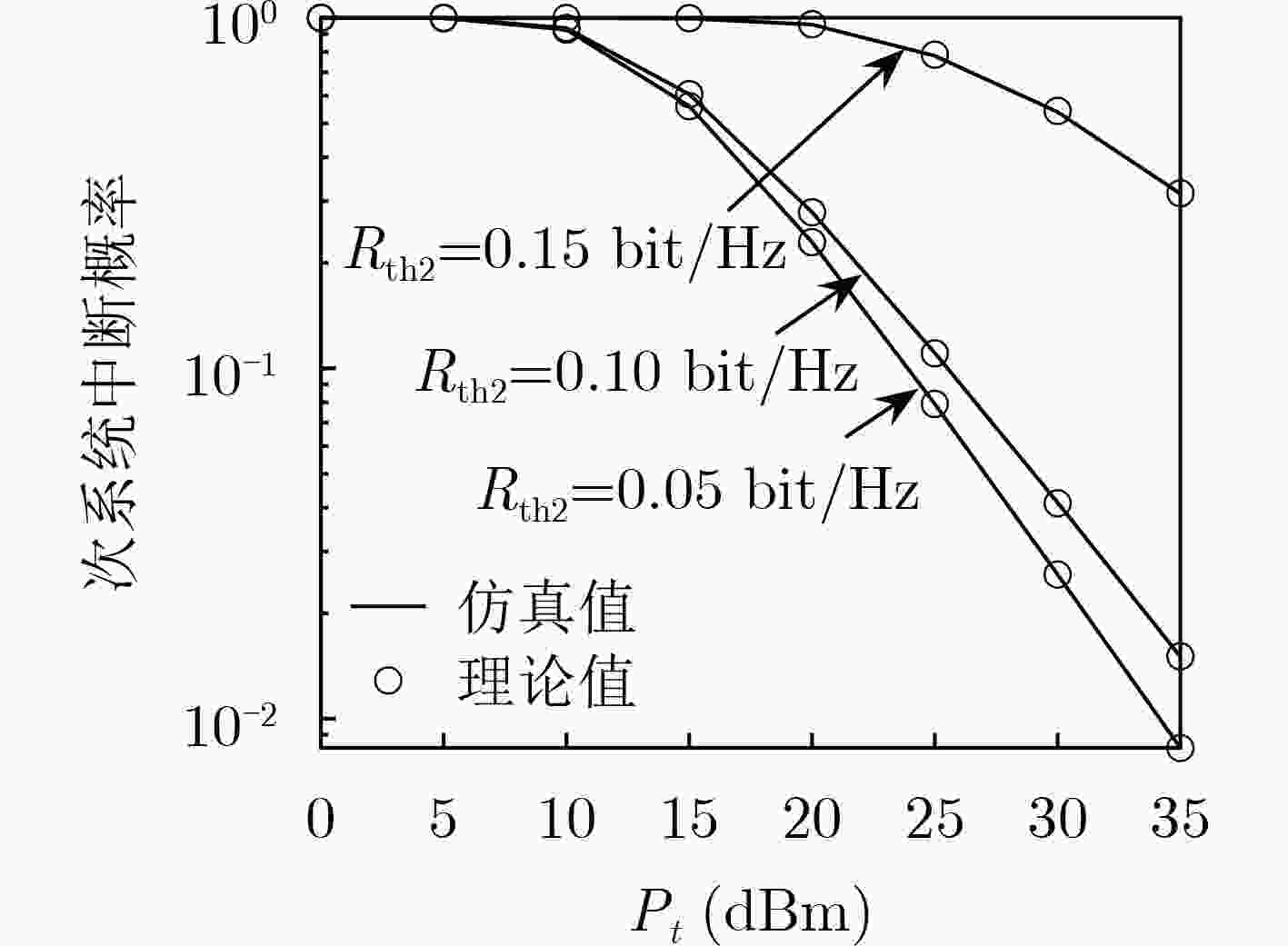
摘要: 该文研究了基于能量收集的互惠共生无线电主、次系统的中断性能。首先,在考虑次用户能量因果约束的基础上给出了主、次系统解码信噪比,并定义了主、次系统的中断概率。在此基础上,推导得到瑞利信道衰落模型下主、次系统的中断概率封闭表达式,进而刻画了主、次系统的分集增益,其结果表明,次用户的接入可以给主系统带来有益的分集增益,即主系统的分集增益由1提升至2。最后,通过仿真验证了理论分析的正确性,并研究了不同系统参数对主、次系统中断概率的影响。Abstract: The outage performance of the primary and secondary systems in a commensal symbiotic radio network with energy harvesting is investigated. First, on the basis of the energy-causality constraint of the secondary user, the signal-to-noise ratios to decode the primary and secondary systems are given, and the outage probabilities of primary and secondary systems are defined. Based on this, closed-form expressions for the outage probability of the primary and secondary systems under the Rayleigh channel fading model are derived, and then the diversity gain of the primary and secondary systems are obtained. It is shown that the access of the secondary users can bring beneficial diversity gain to the primary system, i.e., the diversity gain of the primary system is increased from 1 to 2. Finally, the correctness of the theoretical analysis is verified by simulations, and the effects of different system parameters on the primary and secondary system outage probabilities are investigated.
-
表 1 仿真参数设置
参数名称 参数符号 数值 路径损耗 $v$ 2.7 扩频因子 $N$ 128 PT到CR的距离(m) ${d_{{\text{TR}}}}$ 150 PT到ST的距离(m) ${d_{{\text{TS}}}}$ 10 ST到CR的距离(m) ${d_{{\text{SR}}}}$ 150 高斯白噪声功率(dBm/Hz) ${\sigma ^2}$ –160 反射系数 $\beta $ 0.4 -
[1] IMT-2030(6G)推进组. 6G总体愿景与潜在关键技术白皮书[R]. 2021: 1–32.IMT-2030(6G) Promotion Group. White paper on 6G vision and candidate technologies[R]. 2021: 1–32. [2] NGUYEN D C, DING Ming, PATHIRANA P N, et al. 6G internet of things: A comprehensive survey[J]. IEEE Internet of Things Journal, 2022, 9(1): 359–383. doi: 10.1109/JIOT.2021.3103320 [3] GIORDANI M, POLESE M, MEZZAVILLA M, et al. Toward 6G networks: Use cases and technologies[J]. IEEE Communications Magazine, 2020, 58(3): 55–61. doi: 10.1109/MCOM.001.1900411 [4] ZHANG Lin, LIANG Yingchang, and MING Xiao. Spectrum sharing for internet of things: A survey[J]. IEEE Wireless Communications, 2019, 26(3): 132–139. doi: 10.1109/MWC.2018.1800259 [5] GUO Huayan, LONG Ruizhe, and LIANG Yingchang. Cognitive backscatter network: A spectrum sharing paradigm for passive IOT[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1423–1426. doi: 10.1109/LWC.2019.2919835 [6] LIANG Yingchang, ZHANG Qianqian, LARSSON E G, et al. Symbiotic radio: Cognitive backscattering communications for future wireless networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2020, 6(4): 1242–1255. doi: 10.1109/TCCN.2020.3023139 [7] LIANG Yingchang, LONG Ruizhe, ZHANG Qianqian, et al. Symbiotic communications: Where Marconi meets Darwin[J]. IEEE Wireless Communications, 2022, 29(1): 144–150. doi: 10.1109/MWC.101.2100132 [8] LONG Ruizhe, LIANG Yingchang, GUO Huayan, et al. Symbiotic radio: A new communication paradigm for passive internet of things[J]. IEEE Internet of Things Journal, 2020, 7(2): 1350–1363. doi: 10.1109/JIOT.2019.2954678 [9] ELSAYED M, SAMIR A, EL-BANNA A A A, et al. When NOMA multiplexing meets symbiotic ambient backscatter communication: Outage analysis[J]. IEEE Transactions on Vehicular Technology, 2022, 71(1): 1026–1031. doi: 10.1109/TVT.2021.3127043 [10] YE Yinghui, SHI Liqin, CHU Xiaoli, et al. On the outage performance of ambient backscatter communications[J]. IEEE Internet of Things Journal, 2020, 7(8): 7265–7278. doi: 10.1109/JIOT.2020.2984449 [11] ZHANG Qianqian, LIANG Yingchang, YANG Hongchuan, et al. Mutualistic mechanism in symbiotic radios: When can the primary and secondary transmissions be mutually beneficial?[J]. IEEE Transactions on Wireless Communications, 2022, 21(10): 8036–8050. doi: 10.1109/TWC.2022.3163735 [12] YE Yinghui, SHI Liqin, CHU Xiaoli, et al. Impacts of hardware impairments on mutualistic cooperative ambient backscatter communications[C]. IEEE International Conference on Communications, Seoul, South Korea, 2022. [13] ZHOU Shaoqing, XU Wei, WANG Kezhi, et al. Ergodic rate analysis of cooperative ambient backscatter communication[J]. IEEE Wireless Communications Letters, 2019, 8(6): 1679–1682. doi: 10.1109/LWC.2019.2936196 [14] OPPO研究院. 零功耗通信白皮书[R]. 2022: 1–25.OPPO Research Institute. White paper on zero power communications[R]. 2022: 1–25. [15] WANG Gongpu, GAO Feifei, FAN Rongfei, et al. Ambient backscatter communication systems: Detection and performance analysis[J]. IEEE Transactions on Communications, 2016, 64(11): 4836–4846. doi: 10.1109/TCOMM.2016.2602341 [16] QIAN Jing, GAO Feifei, WANG Gongpu, et al. Noncoherent detections for ambient backscatter system[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1412–1422. doi: 10.1109/TWC.2016.2635654 [17] LV Lu, JIANG Hai, DING Zhiguo, et al. Secrecy-enhancing design for cooperative downlink and uplink NOMA with an untrusted relay[J]. IEEE Transactions on Communications, 2020, 68(3): 1698–1715. doi: 10.1109/TCOMM.2019.2960345 [18] LIU Yingting, YE Yinghui, and HU R Q. Secrecy outage probability in backscatter communication systems with tag selection[J]. IEEE Wireless Communications Letters, 2021, 10(10): 2190–2194. doi: 10.1109/LWC.2021.3095969 -





 下载:
下载:
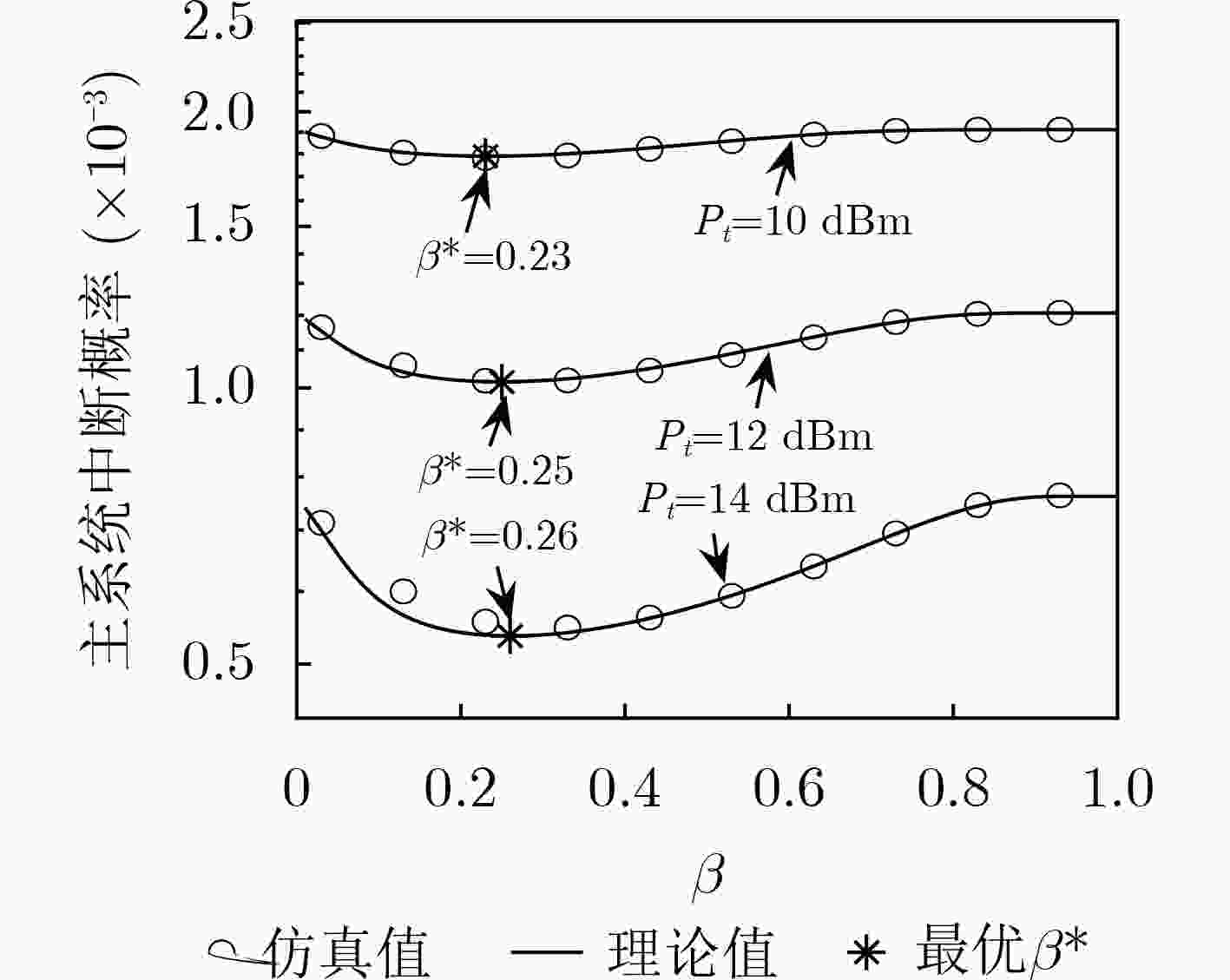


 下载:
下载:
