基于加权正则化协同表示的非均衡分类方法

李艳婷; 王帅; 金军委; 马江涛; 陈雪艳; 陈俊龙

doi:10.11999/JEIT220753

基于加权正则化协同表示的非均衡分类方法

doi: 10.11999/JEIT220753

1.
郑州轻工业大学计算机与通信工程学院郑州 450001
2.
河南工业大学人工智能与大数据学院郑州 450001
3.
华南理工大学计算机科学与工程学院广州 510641

基金项目: 国家自然科学基金(62106233, 62106068)，河南省科技攻关项目(222102210058, 222102210027, 202102210122)

详细信息

作者简介:
李艳婷：女，博士，讲师，研究方向为模式识别、人工智能

王帅：男，硕士生，研究方向为模式识别、机器学习

金军委：男，博士，讲师，研究方向为模式识别、人工智能

马江涛：男，博士，副教授，研究方向为知识图谱、人工智能

陈雪艳：女，博士，讲师，研究方向为通信工程、人工智能

陈俊龙：男，教授，博士生导师，研究方向为宽度学习、人工智能等

通讯作者:
金军委　jinjunwei24@163.com

中图分类号: TP391.4
计量
- 文章访问数: 333
- HTML全文浏览量: 206
- PDF下载量: 76
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-27
- 修回日期: 2023-03-30
- 网络出版日期: 2023-03-31
- 刊出日期: 2023-07-10

Imbalanced Classification Based on Weighted Regularization Collaborative Representation

1.
College of Computer and Communication Engineering , Zhengzhou University of Light Industry, Zhengzhou 450001, China
2.
College of Artifificial Intelligence and Big Data, Henan University of Technology, Zhengzhou 450001, China
3.
School of Computer Science and Engineering, South China University of Technology, Guangzhou 510641, China

Funds: The National Natural Science Foundation of China (62106233, 62106068), The Science and Technology Research Project of Henan Province (222102210058, 222102210027, 202102210122)

摘要

摘要: 协同表示分类器及其变种在模式识别领域展现出优越的识别性能。然而，其成功很大程度上依赖于类别的平衡分布，高度非均衡的类别分布可能会严重影响其有效性。为弥补这一不足，该文把补子空间诱导的正则项引入到协同表示模型框架，使得改进后的正则化模型更具判别性。进一步，为提高非均衡数据集上少数类的识别准确率，根据每类训练样本的表示能力提出一种基于最近子空间的类权学习算法。该算法根据原始数据的先验信息自适应地获取每类的权重并且能够赋予少数类更大的权重，使得最终的分类结果对少数类更加公平。所提模型具有闭式解，这展示了该方法的计算效率。在权威公开的两类和多类非均衡数据集上的实验结果表明所提方法显著优于其他主流非均衡分类算法。
- 非均衡分类 /
- 自适应权重 /
- 补子空间 /
- 协同表示
Abstract: Collaborative representation based classifier and its variants exhibit superior recognition performance in the field of pattern recognition. However, their success relies greatly on the balanced distribution of classes, and a highly imbalanced class distribution may seriously affect their effectiveness. To make up for this defect, this paper introduces the regularization term induced by the complemented subspace into the framework of collaborative representation model, which makes the improved regularization model more discriminative. Furthermore, in order to improve the recognition accuracy of the minority classes on imbalanced datasets, a class weight learning algorithm based on the nearest subspace is proposed according to the representation ability of each class of training samples. The algorithm obtains adaptively the weight of each class and can assign greater weights to the minority classes, so that the final classification results are more fair to the minority classes. The proposed model has a closed-form solution, which demonstrates its computational efficiency. Experimental results on authoritative public binary-class and multi-class imbalanced datasets show that the proposed method outperforms significantly other mainstream imbalanced classification algorithms.
- Imbalanced classification /
- Adaptive weight /
- Complemented subspace /
- Collaborative representation

HTML全文

图 1 CRC在两个非均衡数据集上的混淆矩阵

下载: 全尺寸图片幻灯片

图 2 测试样本在各类训练集中的重构误差占总体重构误差的比重

下载: 全尺寸图片幻灯片

图 3 基于CRC的不同方法在10个非均衡数据集上的对比

下载: 全尺寸图片幻灯片

图 4 WRCR在两个数据集上的混淆矩阵

下载: 全尺寸图片幻灯片

表 1 16个非均衡数据集的详细信息

数据集	类别	样本总数	维度	类别分布	不平衡率
Wine	3	178	13	59: 71: 48	1.48
Glass5	2	214	9	9: 205	22.78
Glass6	2	214	9	29: 185	6.38
Newthyroid1	2	215	5	35: 180	5.14
Newthyroid	3	215	5	150: 35: 30	5.00
Ecoli3	2	336	7	35: 301	8.60
Ecoli	8	336	7	143: 77: 2: 2: 35: 20：5：52	71.51
Dermatology	6	366	33	111: 60: 71: 48: 48: 20	5.55
Penbased	10	1100	16	115: 114: 114: 106: 114: 106: 105: 115: 105: 106	1.10
Shuttle0	2	1829	9	123: 1706	13.87
Ecoli0vs1	2	220	7	77: 143	1.86
Balance-scale	3	625	4	49: 288: 288	5.88
ShuttleC0vsC4	2	1829	9	123: 1706	13.86
Glass4	2	214	9	13: 201	15.46
Glass	3	163	4	70: 76: 17	4.47
Glass016vs2	2	192	9	17: 175	10.29

下载: 导出CSV

表 2 不同方法在Glass5数据集上的运行时间 (s)

	NSC	CRC	CCRC	WRCR
运行时间 (s)	3.19 × 10^–3	4.72 × 10^–3	7.35 × 10^–3	8.07 × 10^–3

下载: 导出CSV

表 3 WRCR与经典非均衡算法在16个数据集上的F-measure (%) 值对比

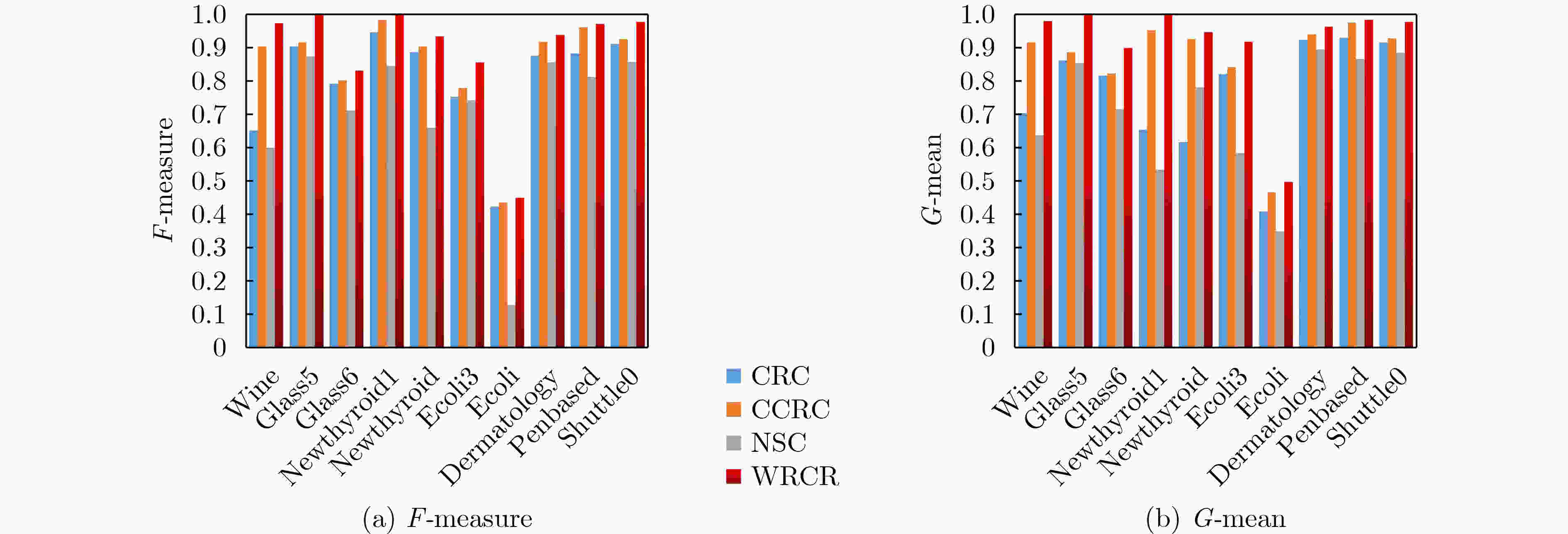
数据集	ADASYN	SMOTEENN	WELM	RUS	SMOTE	MWMOTE	EasyEnsemble	WRCR
Wine	89.01	87.12	88.63	89.05	89.03	89.82	89.51	100.00
Glass5	77.44	77.86	64.31	87.15	68.72	79.22	88.42	100.00
Glass6	88.61	89.23	82.72	82.51	83.14	83.52	85.42	90.04
Newthyroid1	97.52	97.93	97.05	94.52	95.46	92.17	94.34	100.00
Newthyroid	92.55	92.61	90.44	93.26	91.72	92.81	93.22	94.77
Ecoli3	87.61	86.63	88.62	84.13	87.46	81.13	88.22	98.35
Ecoli	29.91	38.92	30.14	35.32	33.90	34.82	27.14	53.10
Dermatology	92.81	89.91	91.33	92.37	92.24	92.11	78.72	96.25
Penbased	95.63	97.52	97.85	97.31	98.40	95.82	90.52	98.40
Shuttle0	88.42	84.62	97.41	80.43	82.72	81.32	89.41	97.87
Ecoli0vs1	95.72	94.17	98.51	91.34	94.69	96.56	97.75	100.00
Balance-scale	54.26	52.47	51.38	47.59	50.58	54.63	55.76	61.70
ShuttleC0vsC4	93.96	89.35	96.47	91.25	85.19	93.42	81.38	97.89
Glass4	90.33	93.66	91.34	92.48	90.33	94.16	94.42	96.18
Glass	48.59	51.36	54.81	48.75	49.65	50.23	51.48	56.06
Glass016vs2	58.11	59.19	83.77	62.47	61.36	69.82	66.78	84.09

下载: 导出CSV

表 4 WRCR与经典非均衡算法在16个数据集上的G-mean (%) 值对比

数据集	ADASYN	SMOTEENN	WELM	RUS	SMOTE	MWMOTE	EasyEnsemble	WRCR
Wine	84.11	80.63	94.51	83.15	83.41	84.53	88.62	100.00
Glass5	88.13	90.52	88.92	91.24	87.52	89.74	88.64	100.00
Glass6	88.64	89.22	82.73	82.53	83.16	83.01	85.41	83.33
Newthyroid1	95.65	98.23	97.44	96.82	95.07	94.42	94.33	100.00
Newthyroid	90.53	90.42	89.91	87.23	91.74	92.43	89.14	93.63
Ecoli3	83.02	82.51	84.83	82.32	84.23	82.83	84.63	87.49
Ecoli	62.31	46.54	38.92	36.74	60.05	60.22	33.86	50.07
Dermatology	87.32	81.43	87.25	76.13	86.34	89.73	74.14	93.98
Penbased	91.83	95.52	95.36	91.51	94.34	93.15	87.92	97.18
Shuttle0	87.61	97.21	97.41	97.65	84.81	85.20	92.41	97.87
Ecoli0vs1	91.54	90.34	98.55	89.23	91.38	94.76	94.84	100.00
Balance-scale	52.83	54.37	50.65	48.98	54.76	52.42	55.78	61.68
ShuttleC0vsC4	92.51	86.76	92.36	90.18	83.57	91.83	87.38	97.87
Glass4	54.47	51.85	61.18	53.32	52.49	57.39	59.42	66.66
Glass	42.36	40.46	39.47	36.53	39.76	38.76	41.04	44.01
Glass016vs2	45.48	47.69	47.89	45.83	49.67	51.28	53.89	66.66

下载: 导出CSV

表 5 WRCR与先进非均衡算法的G-mean (%) 值对比

数据集	GDO	VW-ELM	GEP	GMBSCL	GSE	WRCR
Glass5	84.10	97.51	95.85	91.50	–	100.00
Newthyroid1	89.99	99.52	97.33	–	–	100.00
Ecoli0vs1	95.16	98.64	98.32	98.31	97.58	100.00
Ecoli3	88.67	91.20	92.57	–	88.53	98.35

下载: 导出CSV

参考文献(23)

[1]	SHU Ting, ZHANG B, and TANG Yuanyan. Sparse supervised representation-based classifier for uncontrolled and imbalanced classification[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(8): 2847–2856. doi: 10.1109/TNNLS.2018.2884444
[2]	JIN Junwei, LI Yanting, and CHEN C L P. Pattern classification with corrupted labeling via robust broad learning system[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(10): 4959–4971. doi: 10.1109/TKDE.2021.3049540
[3]	JIN Junwei, LI Yanting, YANG Tiejun, et al. Discriminative group-sparsity constrained broad learning system for visual recognition[J]. Information Sciences, 2021, 576: 800–818. doi: 10.1016/j.ins.2021.06.008
[4]	JIN Junwei, QIN Zhenhao, YU Dengxiu, et al. Regularized discriminative broad learning system for image classification[J]. Knowledge-Based Systems, 2022, 251: 109306. doi: 10.1016/j.knosys.2022.109306
[5]	ZHU Zonghai, WANG Zhe, LI Dongdong, et al. Globalized multiple balanced subsets with collaborative learning for imbalanced data[J]. IEEE Transactions on Cybernetics, 2022, 52(4): 2407–2417. doi: 10.1109/TCYB.2020.3001158
[6]	ZHU Zonghai, WANG Zhe, LI Dongdong, et al. Geometric structural ensemble learning for imbalanced problems[J]. IEEE Transactions on Cybernetics, 2020, 50(4): 1617–1629. doi: 10.1109/TCYB.2018.2877663
[7]	CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321–357. doi: 10.1613/jair.953
[8]	HE Haibo, BAI Yang, GARCIA E A, et al. ADASYN: Adaptive synthetic sampling approach for imbalanced learning[C]. Proceedings of the International Joint Conference on Neural Networks, Hong Kong, China, 2008: 1322–1328.
[9]	BARUA S, ISLAM M M, YAO Xin, et al. MWMOTE: Majority weighted minority oversampling technique for imbalanced data set learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 405–425. doi: 10.1109/TKDE.2012.232
[10]	BATISTA G E A P A, PRATI R C, and MONARD M C. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6(1): 20–29. doi: 10.1145/1007730.1007735
[11]	DOUZAS G and BACAO F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE[J]. Information Sciences, 2019, 501: 118–135. doi: 10.1016/j.ins.2019.06.007
[12]	WANG Xinyue, XU Jian, ZENG Tieyong, et al. Local distribution-based adaptive minority oversampling for imbalanced data classification[J]. Neurocomputing, 2021, 422: 200–213. doi: 10.1016/j.neucom.2020.05.030
[13]	CHEN Baiyun, XIA Shuyin, CHEN Zizhong, et al. RSMOTE: A self-adaptive robust SMOTE for imbalanced problems with label noise[J]. Information Sciences, 2021, 553: 397–428. doi: 10.1016/j.ins.2020.10.013
[14]	XIE Yuxi, QIU Min, ZHANG Haibo, et al. Gaussian distribution based oversampling for imbalanced data classification[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(2): 667–679. doi: 10.1109/TKDE.2020.2985965
[15]	CAO Changjie, CUI Zongyong, WANG Liying, et al. Cost-sensitive awareness-based SAR automatic target recognition for imbalanced data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1–16. doi: 10.1109/TGRS.2021.3068447
[16]	ZONG Weiwei, HUANG Guangbin, and CHEN Yiqiang. Weighted extreme learning machine for imbalance learning[J]. Neurocomputing, 2013, 101: 229–242. doi: 10.1016/j.neucom.2012.08.010
[17]	LIU Zheng, JIN Wei, and MU Ying. Variances-constrained weighted extreme learning machine for imbalanced classification[J]. Neurocomputing, 2020, 403: 45–52. doi: 10.1016/j.neucom.2020.04.052
[18]	ZHANG Lei, YANG Meng, and FENG Xiangchu. Sparse representation or collaborative representation: Which helps face recognition[C]. Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 2011: 471–478.
[19]	YUAN Haoliang, LI Xuecong, XU Fangyuan, et al. A collaborative-competitive representation based classifier model[J]. Neurocomputing, 2018, 275: 627–635. doi: 10.1016/j.neucom.2017.09.022
[20]	LI Yanting, JIN Junwei, ZHAO Liang, et al. A neighborhood prior constrained collaborative representation for classification[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2021, 19(2): 2050073. doi: 10.1142/S0219691320500733
[21]	KHAN M M R, ARIF R B, SIDDIQUE M A B, et al. Study and observation of the variation of accuracies of KNN, SVM, LMNN, ENN algorithms on eleven different datasets from UCI machine learning repository[C]. Proceedings of the 4th International Conference on Electrical Engineering and Information & Communication Technology. Dhaka, Bangladesh, 2018: 124–129.
[22]	LIU Xuying, WU Jianxin, and ZHOU Zhihua. Exploratory undersampling for class-imbalance learning[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(2): 539–550. doi: 10.1109/TSMCB.2008.2007853
[23]	JEDRZEJOWICZ J and JEDRZEJOWICZ P. GEP-based classifier for mining imbalanced data[J]. Expert Systems with Applications, 2021, 164: 114058. doi: 10.1016/j.eswa.2020.114058