Spiking Neural Network Robot Tactile Object Recognition Method with Regularization Constraints
-
摘要: 拓展触觉感知能力是智能机器人未来发展的重要方向之一,决定着机器人的应用场景范围。由触觉传感器采集的数据是机器人完成触觉感知任务基础,但触觉数据具有复杂的时空性。脉冲神经网络具有丰富的时空动力学特征和契合硬件的事件驱动性,能更好地处理时空信息和应用于人工智能芯片给机器人带来更高能效。该文针对脉冲神经网络神经元脉冲活动离散性导致网络训练过程反向传播失效的问题,从智能触觉机器人动态系统角度,引入脉冲活动近似函数使脉冲神经网络反向传播梯度下降法有效;针对触觉脉冲数据量少导致的过拟合问题,融合正则化方法加以缓解;最后,提出具有正则化约束的脉冲神经网络机器人触觉物体识别(Spiking neural network Tactile dropout, SnnTd; Spiking neural network Tactile dropout-l2-cosine annealing, SnnTdlc)算法。相较于经典方法TactileSGNet, Grid-based CNN, MLP和GCN, SnnTd正则化方法触觉物体识别率在EvTouch-Containers数据集上比最好方法TactileSGNet提升了5.00%,SnnTdlc正则化方法触觉物体识别率在EvTouch-Objects数据集上比最好方法TactileSGNet提升了3.16%。Abstract: It is important for the future development of intelligent robots to expand tactile perception ability, which determines the scope of application scenarios for robots. Tactile data collected by tactile sensors are the basis of robotics work, but these data have complex spatio-temporal properties. Spiking neural network has rich spatio-temporal dynamics and event-driven nature. It can better process spatio-temporal information and be applied to artificial intelligence chips to bring higher energy efficiency to robots. To solve the problem of backpropagation failure in the network training process caused by the discreteness of neuron spike activity in the spiking neural network, from the perspective of the dynamic system of the intelligent robot, the spiking activity approximation function is introduced to make the spiking neural network back-propagation gradient descent method effective. The over-fitting problem caused by the small amount of tactile data is alleviated by the regularization methods. Finally, the spiking neural network robot tactile object recognition algorithm SnnTd and SnnTdlc with regularization constraints are proposed. Compared with the classical methods TactileSGNet, Grid-based CNN, MLP and GCN, the SnnTd method tactile object recognition rate is improved by 5.00% over the best method TactileSGNet on EvTouch-Containers dataset, and the SnnTdlc method tactile object recognition rate is improved by 3.16% over the best method TactileSGNet on EvTouch-Objects dataset.
-
算法1 具有L2正则化约束的脉冲神经网络机器人
触觉物体识别算法相关参数:学习率${\mu _t}$, 网络参数$w$和$b$,时间步长$T$,触觉脉冲数
据$S = \left\{ {{S_1},{S_2},\cdots,{S_T}} \right\}$,目标输出
$R = \left\{ {{R_1},{R_2},\cdots,{R_T}} \right\}$,权重衰减参数$\sigma $,损失函数
$L = L(R,S) + \dfrac{\sigma }{2}{\left\| w \right\|^2}$初始化:$w$,$b$,空列表$K = \{ \} $ for ${\rm{Epoch}} = 1,2, \cdots ,N$: for $t = 1,2, \cdots ,T$: (1) 输入${S_t}$到脉冲神经网络,获得输出脉冲${K_t}$,将${K_t}$添
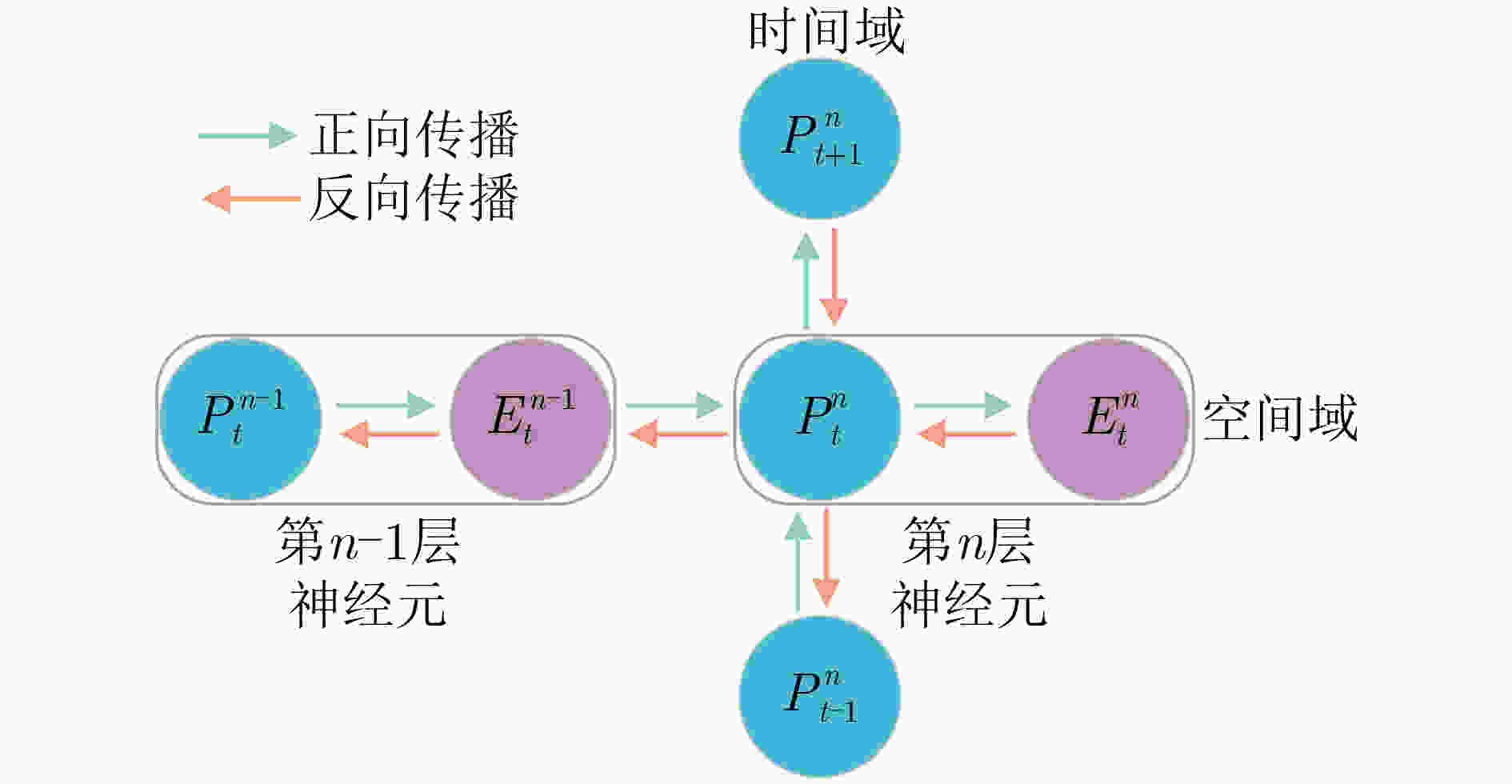
加到$K$;end (2) 计算损失$L = L(R,S) + \dfrac{\sigma }{2}{\left\| w \right\|^2}$; (3) 计算 $\dfrac{{\partial \left(L + \dfrac{\sigma }{2}{{\left\| w \right\|}^2}\right)}}{{\partial w}} = \displaystyle\sum\nolimits_{t = 1}^T {\dfrac{{\partial L}}{{\partial P_t^n}}E_t^{n - 1}} + \sigma w$,
$\dfrac{{\partial (L + \dfrac{\sigma }{2}{{\left\| w \right\|}^2})}}{{\partial b}} = \displaystyle\sum\nolimits_{t = 1}^T {\dfrac{{\partial L}}{{\partial P_t^n}}} $;(4) 根据Adam优化算法进行更新; (5) 通过余弦退火算法更新学习率${\mu _t}$; (6) 更新参数$w$,$b$; end 表 1 超参数设置表
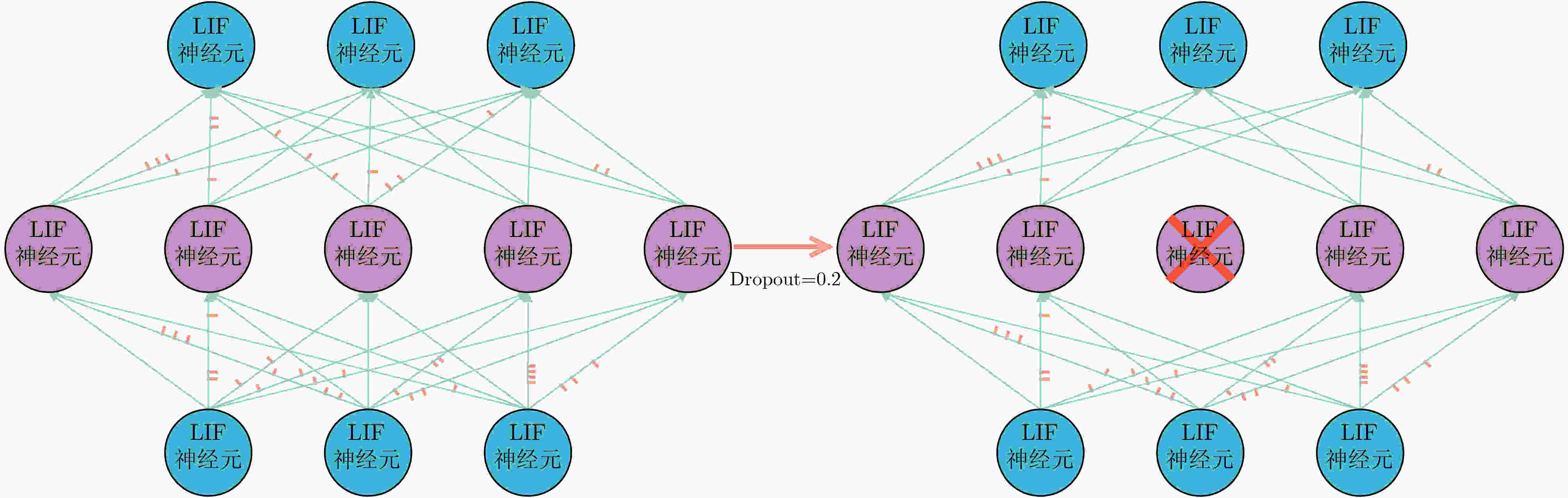
参数 值 参数 值 Epochs 100 宽度系数$a$ 0.5 初始学习率${\rm{lr}}$ 1×10–3 dropout1 0.2 学习率衰减因子$\alpha $ 0.1 dropout2 0.5 学习率衰减代数${\rm{lrEpochs}}$ 40 动量${\beta _1}$ 0.9 余弦退火最小学习率${{\rm{lr}}_{ {\text{min} } } }$ 5×10–6 均方根传播${\beta _2}$ 0.999 膜电位阈值${P_{{\text{TH}}}}$ 0.5 权重衰减$\sigma $ 0.01 表 2 EvTouch-Containers数据集实验结果
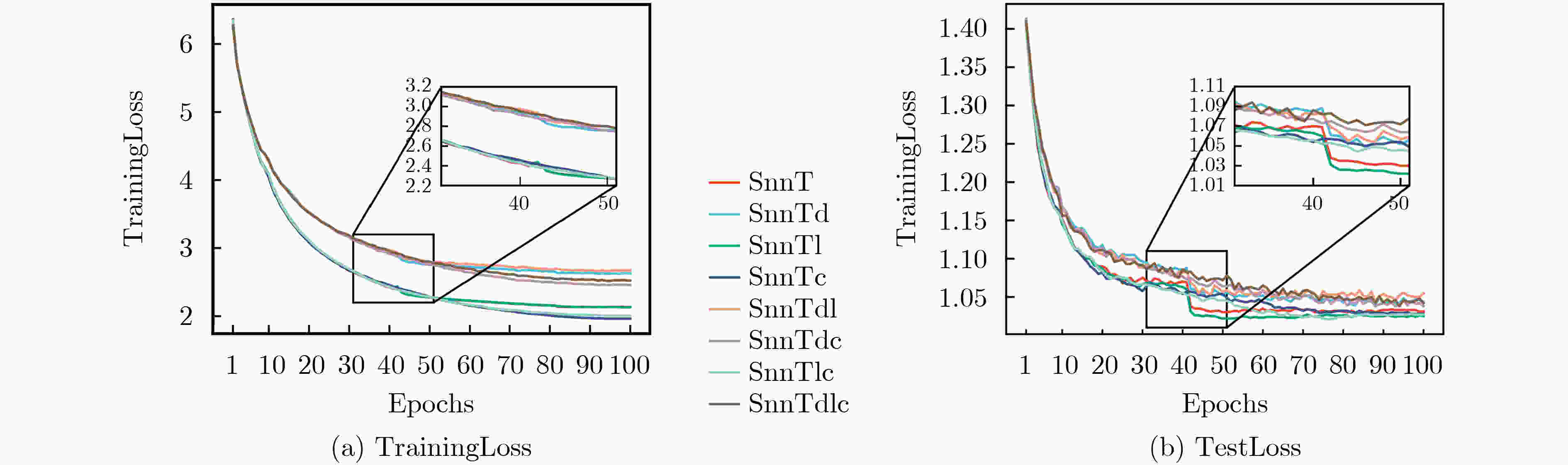
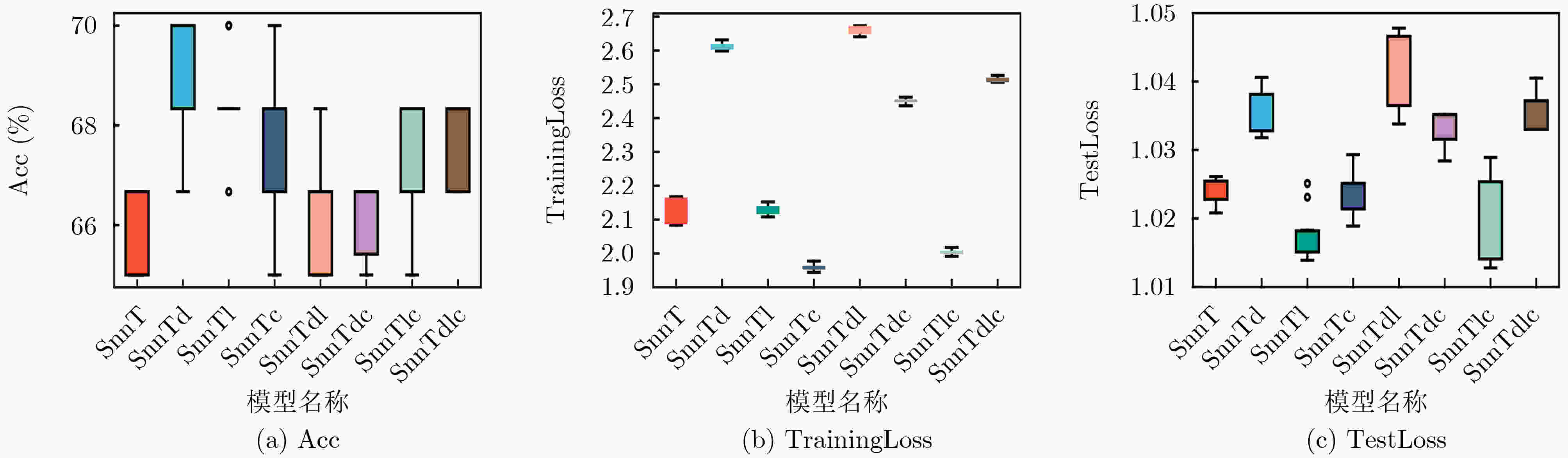
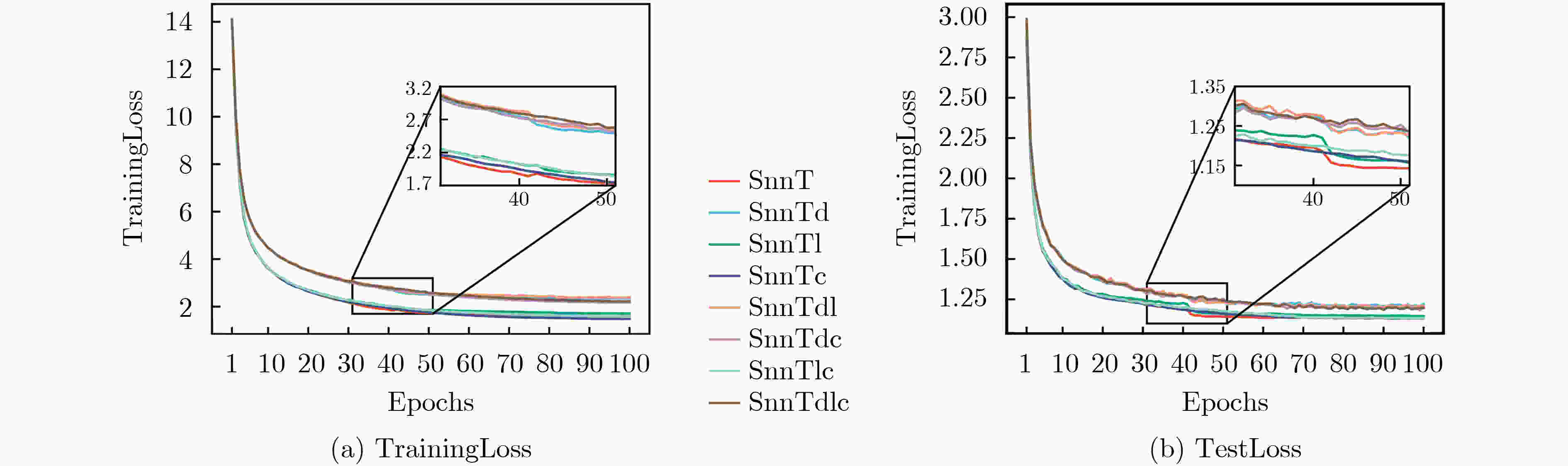
模型 方法 Acc(%) TrainingLoss TestLoss Dropout L2 Cosine Annealing SnnT 66.00±0.86 2.13±0.04 1.03±0.01 SnnTd √ 69.17±1.18 2.61±0.01 1.04±0.01 SnnTl √ 68.33±1.11 2.13±0.02 1.02±0.01 SnnTc √ 67.17±1.58 1.96±0.01 1.03±0.01 SnnTdl √ √ 66.33±1.32 2.67±0.01 1.04±0.01 SnnTdc √ √ 66.17±0.81 2.45±0.01 1.03±0.01 SnnTlc √ √ 67.17±1.37 2.01±0.01 1.02±0.01 SnnTdlc √ √ √ 67.33±0.86 2.51±0.01 1.04±0.01 表 3 EvTouch-Objects数据集实验结果
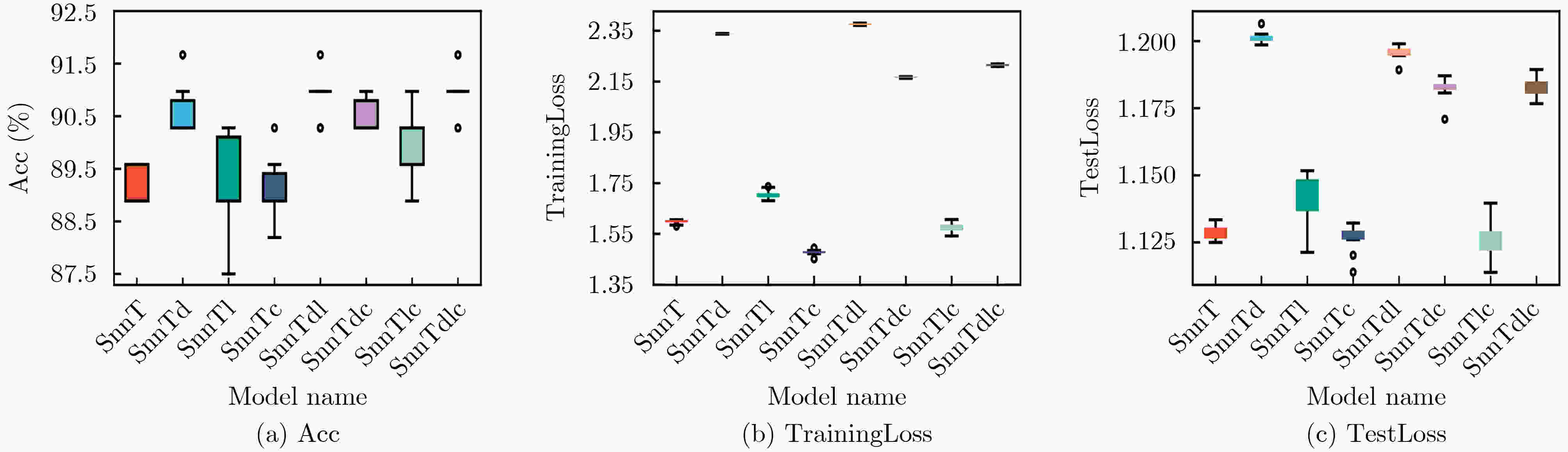
模型 方法 Acc(%) TrainingLoss TestLoss Dropout L2 Cosine Annealing SnnT 89.17±0.36 1.60±0.01 1.13±0.01 SnnTd √ 90.63±0.59 2.34±0.01 1.20±0.01 SnnTl √ 89.31±0.88 1.71±0.02 1.14±0.01 SnnTc √ 89.10±0.57 1.48±0.01 1.12±0.01 SnnTdl √ √ 90.90±0.39 2.38±0.01 1.20±0.01 SnnTdc √ √ 90.49±0.33 2.17±0.01 1.18±0.01 SnnTlc √ √ 89.86±0.67 1.58±0.02 1.12±0.01 SnnTdlc √ √ √ 91.04±0.39 2.22±0.01 1.18±0.01 表 4 SnnTdlc模型与经典方法在两个数据集下Acc的实验结果(%)
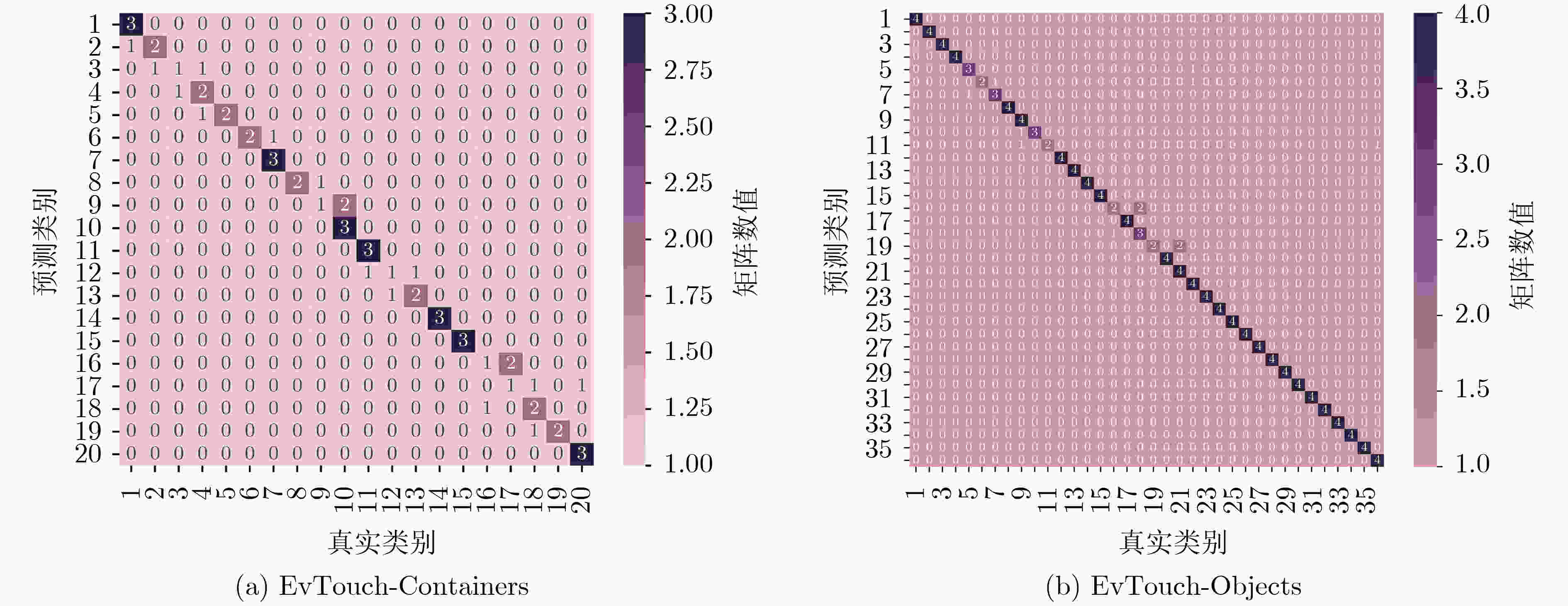
模型 EvTouch-Containers EvTouch-Objects TactileSGNet 64.17±2.75 89.44±0.55 Grid-based CNN 60.17±2.78 88.40±1.14 MLP 58.83±2.49 85.97±0.85 GCN 58.83±2.84 85.14±1.51 SnnTd 69.17±1.18 90.63±0.59 SnnTdlc 67.33±0.86 91.04±0.39 -
[1] LI Qiang, KROEMER O, SU Zhe, et al. A review of tactile information: Perception and action through touch[J]. IEEE Transactions on Robotics, 2020, 36(6): 1619–1634. doi: 10.1109/TRO.2020.3003230 [2] WANG Chunfeng, DONG Lin, PENG Dengfeng, et al. Tactile sensors for advanced intelligent systems[J]. Advanced Intelligent Systems, 2019, 1(8): 1900090. doi: 10.1002/aisy.201900090 [3] DAHIYA R S, METTA G, VALLE M, et al. Tactile sensing—from humans to humanoids[J]. IEEE Transactions on Robotics, 2010, 26(1): 1–20. doi: 10.1109/TRO.2009.2033627 [4] AHMADI R, PACKIRISAMY M, DARGAHI J, et al. Discretely loaded beam-type optical fiber tactile sensor for tissue manipulation and palpation in minimally invasive robotic surgery[J]. IEEE Sensors Journal, 2012, 12(1): 22–32. doi: 10.1109/JSEN.2011.2113394 [5] YEH S K, HSIEH M L, and FANG W. CMOS-based tactile force sensor: A review[J]. IEEE Sensors Journal, 2021, 21(11): 12563–12577. doi: 10.1109/JSEN.2021.3060539 [6] 程龙, 刘泽宇. 柔性触觉传感技术及其在医疗康复机器人的应用[J]. 控制与决策, 2022, 37(6): 1409–1432. doi: 10.13195/j.kzyjc.2021.1896CHENG Long and LIU Zeyu. Flexible tactile sensing technology and its application in medical rehabilitation robots[J]. Control and Decision, 2022, 37(6): 1409–1432. doi: 10.13195/j.kzyjc.2021.1896 [7] DAHIYA R, YOGESWARAN N, LIU Fengyuan, et al. Large-area soft e-skin: The challenges beyond sensor designs[J]. Proceedings of the IEEE, 2019, 107(10): 2016–2033. doi: 10.1109/JPROC.2019.2941366 [8] SUNDARAM S, KELLNHOFER P, LI Yunzhu, et al. Learning the signatures of the human grasp using a scalable tactile glove[J]. Nature, 2019, 569(7758): 698–702. doi: 10.1038/s41586-019-1234-z [9] KIM K, SIM M, LIM S H, et al. Tactile avatar: Tactile sensing system mimicking human tactile cognition[J]. Advanced Science, 2021, 8(7): 2002362. doi: 10.1002/advs.202002362 [10] ZHU Minglu, SUN Zhongda, ZHANG Zixuan, et al. Haptic-feedback smart glove as a creative human-machine interface (HMI) for virtual/augmented reality applications[J]. Science Advances, 2020, 6(19): z8693. doi: 10.1126/sciadv.aaz8693 [11] YAN Youcan, HU Zhe, YANG Zhengbao, et al. Soft magnetic skin for super-resolution tactile sensing with force self-decoupling[J]. Science Robotics, 2021, 6(51): c8801. doi: 10.1126/scirobotics.abc8801 [12] BARTOLOZZI C, ROS P M, DIOTALEVI F, et al. Event-driven encoding of off-the-shelf tactile sensors for compression and latency optimisation for robotic skin[C]. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver, Canada, 2017: 166–173. [13] DAVIES M, WILD A, ORCHARD G, et al. Advancing neuromorphic computing with Loihi: A survey of results and outlook[J]. Proceedings of the IEEE, 2021, 109(5): 911–934. doi: 10.1109/JPROC.2021.3067593 [14] DAVIES M, SRINIVASA N, LIN T H, et al. Loihi: A neuromorphic manycore processor with on-chip learning[J]. IEEE Micro, 2018, 38(1): 82–99. doi: 10.1109/MM.2018.112130359 [15] 胡一凡, 李国齐, 吴郁杰, 等. 脉冲神经网络研究进展综述[J]. 控制与决策, 2021, 36(1): 1–26. doi: 10.13195/j.kzyjc.2020.1006HU Yifan, LI Guoqi, WU Yujie, et al. Spiking neural networks A survey on recent advances and new directions[J]. Control and Decision, 2021, 36(1): 1–26. doi: 10.13195/j.kzyjc.2020.1006 [16] 张铁林, 徐波. 脉冲神经网络研究现状及展望[J]. 计算机学报, 2021, 44(9): 1767–1785. doi: 10.11897/SP.J.1016.2021.01767ZHANG Tielin and XU Bo. Research advances and perspectives on spiking neural networks[J]. Chinese Journal of Computers, 2021, 44(9): 1767–1785. doi: 10.11897/SP.J.1016.2021.01767 [17] BARBIER T, TEULIÈRE C, and TRIESCH J. Spike timing-based unsupervised learning of orientation, disparity, and motion representations in a spiking neural network[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 1377–1386. [18] PAREDES-VALLÉS F, SCHEPER K Y, and DE CROON G C. Unsupervised learning of a hierarchical spiking neural network for optical flow estimation: From events to global motion perception[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2051–2064. doi: 10.1109/TPAMI.2019.2903179 [19] HAN Bing, SRINIVASAN G, and ROY K. RMP-SNN: Residual membrane potential neuron for enabling deeper high-accuracy and low-latency spiking neural network[C]. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 13555–13564. [20] DENG Lei, WU Yujie, HU Xing, et al. Rethinking the performance comparison between SNNS and ANNS[J]. Neural Networks, 2020, 121: 294–307. doi: 10.1016/j.neunet.2019.09.005 [21] LEE J H, DELBRUCK T, and PFEIFFER M. Training deep spiking neural networks using backpropagation[J]. Frontiers in Neuroscience, 2016, 10: 508. doi: 10.3389/fnins.2016.00508 [22] WU Yujie, DENG Lei, LI Guoqi, et al. Direct training for spiking neural networks: Faster, larger, better[C]. Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, Honolulu, USA, 2019: 1311–1318. [23] SEE H H, LIM B, LI Si, et al. ST-MNIST-the spiking tactile MNIST neuromorphic dataset[J]. arXiv: 2005.04319, 2020. [24] TAUNYAZOV T, CHUA Yansong, GAO Ruihan, et al. Fast texture classification using tactile neural coding and spiking neural network[C]. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, USA, IEEE, 2020: 9890–9895. [25] TAUNYAZOV T, SNG W, SEE H H, et al. Event-driven visual-tactile sensing and learning for robots[J]. arXiv: 2009.07083, 2020. [26] GU Fuqaing, SNG Weicong, TAUNYAZOV T, et al. TactileSGNet: A spiking graph neural network for event-based tactile object recognition[C]. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, USA, 2020: 9876–9882. [27] SUSHKO V, GALL J, and KHOREVA A. One-shot GAN: Learning to generate samples from single images and videos[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 2596–2600. [28] 程曦, 张志勇. 基于人工神经网络的复杂介质中波的传播不确定性分析方法[J]. 电子与信息学报, 2021, 43(12): 3662–3670. doi: 10.11999/JEIT200755CHENG Xi and ZHANG Zhiyong. An uncertainty analysis method of wave propagation in complex media based on artificial neural network[J]. Journal of Electronics &Information Technology, 2021, 43(12): 3662–3670. doi: 10.11999/JEIT200755 [29] 曹毅, 费鸿博, 李平, 等. 基于多流卷积和数据增强的声场景分类方法[J]. 华中科技大学学报(自然科学版), 2022, 50(4): 40–46. doi: 10.13245/j.hust.220407CAO Yi, FEI Hongbo, LI Ping, et al. Acoustic scene classification method based on multi-stream convolution and data augmentation[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2022, 50(4): 40–46. doi: 10.13245/j.hust.220407 [30] GAL Y and GHAHRAMANI Z. Dropout as a Bayesian approximation: representing model uncertainty in deep learning[C]. Proceedings of the 33rd International Conference on Machine Learning, New York, USA, 2016: 1050–1059. [31] 李翔, 陈硕, 杨健. 泛化界正则项: 理解权重衰减正则形式的统一视角[J]. 计算机学报, 2021, 44(10): 2122–2134. doi: 10.11897/SP.J.1016.2021.02122LI Xiang, CHEN Shuo, and YANG Jian. Generalization bound Regularizer: A unified perspective for understanding weight decay[J]. Chinese Journal of Computers, 2021, 44(10): 2122–2134. doi: 10.11897/SP.J.1016.2021.02122 [32] KINGMA D P and BA J. Adam: A method for stochastic optimization[J]. arXiv: 1412.6980v9, 2014. [33] LOSHCHILOV I and HUTTER F. SGDR: Stochastic gradient descent with warm restarts[J]. arXiv: 1608.03983v3, 2016. -






 下载:
下载:


 下载:
下载:
