3D Parameters Estimation of Helicopter with Constant Speed Using Single Hydrophone
-
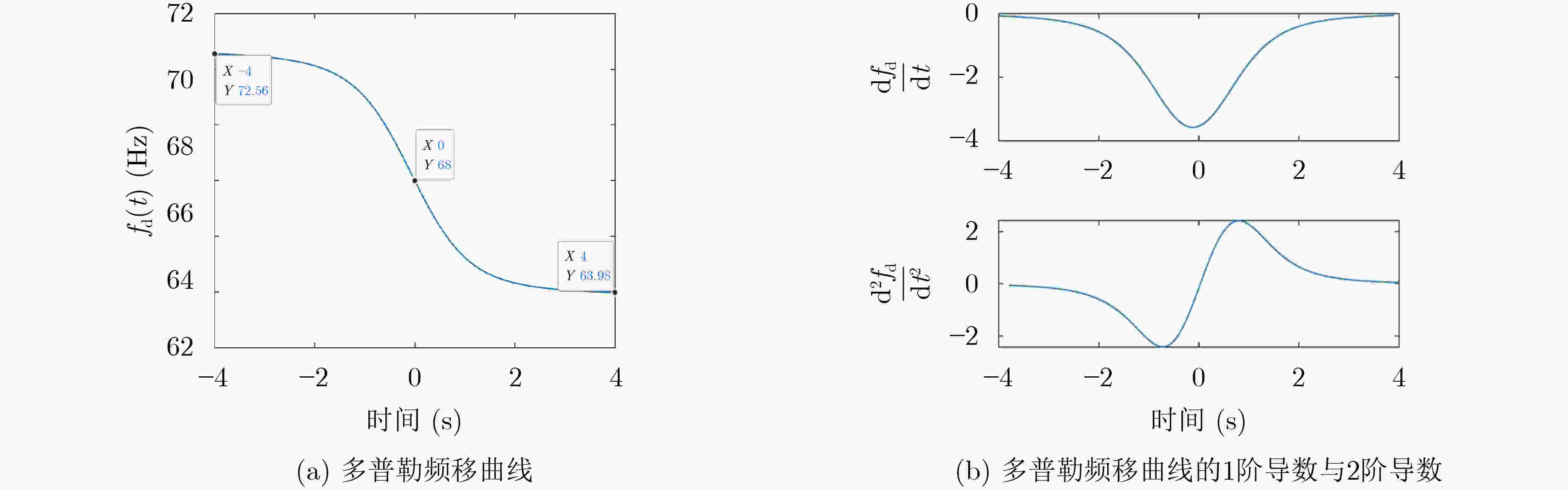
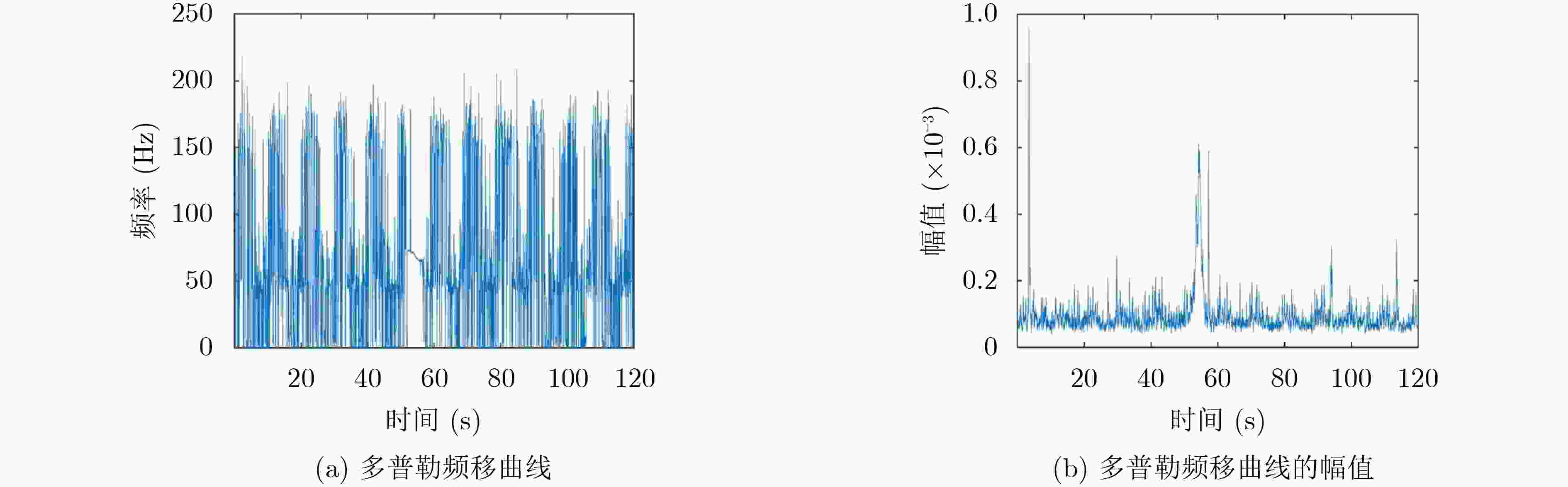
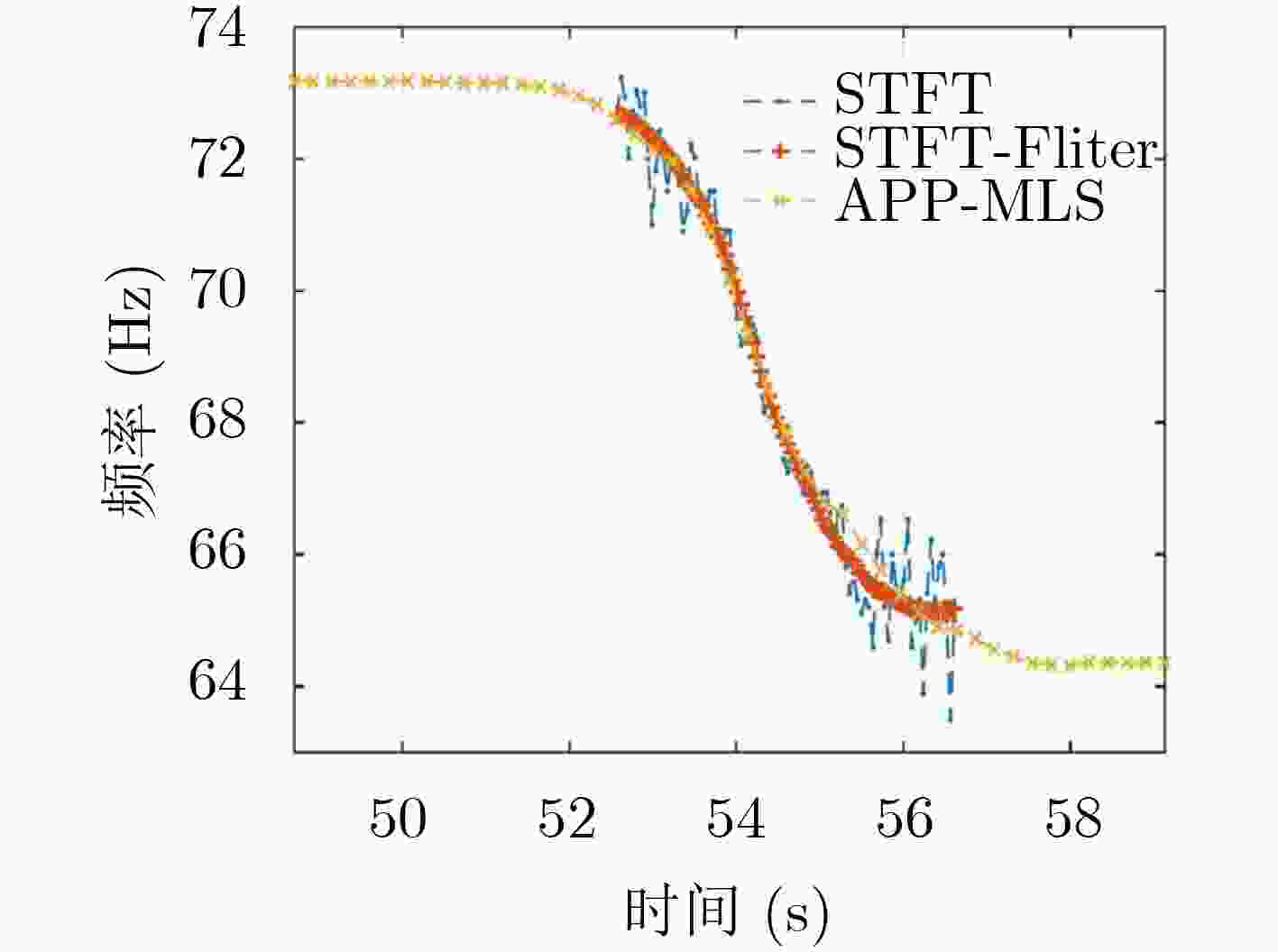
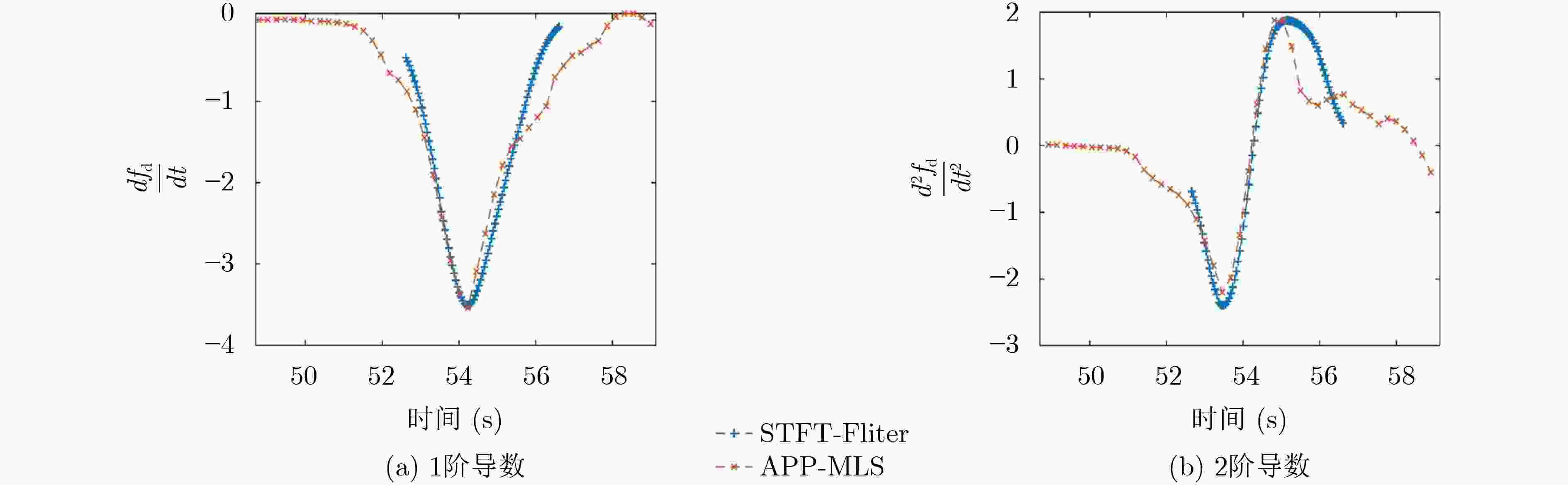
摘要: 针对空中匀速飞行运动目标所激发的水声信号特征,该文将传统的2维平面内估计目标飞行高度、速度等参数的问题扩展到3维空间,可以求解飞行时偏航距离,更符合实际情况,解决了空中快速飞行目标状态3维参数估计问题。该文首先以直升机离散线谱为特征声源,建立其在空气-水两层介质中声学多普勒的3维传播模型,考虑了目标的飞行速度、高度和偏离水听器的偏航距离。然后根据多普勒频移曲线及其1阶、2阶导数的不对称性,推导出水下探空应用中飞行器的3维参数估计方法。最后,通过分析单水听器接收的实测信号,验证了文章构建3维空间多普勒频移飞行参数估计模型的合理性及APP-LMS算法相较于短时傅里叶瞬时频率估计算法能够更准确反演直升机的航行参数。Abstract: The three-dimensional parameter estimation algorithm of the helicopter with constant speed flight from the underwater acoustic data with single hydrophone, which extended the traditional two-dimension flight parameters estimation is proposed. Firstly, the helicopter line spectrum is used as the exciting sound source, and its three-dimensional Doppler propagation model in two-layer air-water medium, including altitude, speed and deviation distance of the helicopter, is established. The asymmetry of the Doppler frequency curve and its first- and second-order derivatives is related with the three-dimensional motion parameter of the helicopter, which can be estimated from the received data. Finally, with the measured data, the rationality of the three-dimensional Doppler shift flight model is verified and the result is compared with short-time Fourier instantaneous frequency estimation algorithm, APP-LMS algorithm can more accurately retrieve the flight parameters such as natural frequency, velocity, altitude and yaw distance of the helicopter.
-
表 1 各参数在穿过CPA点前后的变化规律
位置 从负无穷至CPA CPA 从CPA至正无穷 $ t $(s) $ - \infty \to 0 $ 0 $ 0 \to + \infty $ $ \alpha \left( t \right) $(s) $ 0 \to {{\pi} \mathord{\left/ {\vphantom {{\pi} 2}} \right. } 2} $ $ {{\pi} \mathord{\left/ {\vphantom {{\pi} 2}} \right. } 2} $ $ {{\pi} \mathord{\left/ {\vphantom {{\pi} 2}} \right. } 2} \to {\pi} $ $ {\theta _{\text{I}}}\left( t \right) $(s) $ \arcsin {\text{n}} \to \dfrac{{\pi}}{{\text{2}}} - \arctan \dfrac{h}{{{w_{{\text{amin}}}}}} $ $ \dfrac{{\pi}}{2} - \arctan \dfrac{h}{{{w_{{\text{amin}}}}}} $ $\dfrac{ {\pi} }{2} - \arctan \dfrac{h}{ { {w_{ {\text{amin} } } } } } \to \arcsin {{n} }$ $ {\theta _{\text{T}}}\left( t \right) $(s) $ \dfrac{{\pi}}{2} \to \dfrac{{\pi}}{2} - \arctan \dfrac{d}{{{w_{{\text{wmin}}}}}} $ $ \dfrac{{\pi}}{2} - \arctan \dfrac{d}{{{w_{{\text{wmin}}}}}} $ $ \dfrac{{\pi}}{2} - \arctan \dfrac{d}{{{w_{{\text{wmin}}}}}} \to \dfrac{{\pi}}{2} $ -
[1] 修建娟, 张敬艳, 董凯. 基于动力学模型约束的空间目标精确跟踪算法研究[J]. 电子学报, 2021, 49(4): 781–787. doi: 10.12263/DZXB.20200336XIU Jianjuan, ZHANG Jingyan, and DONG Kai. Precise tracking algorithm of space target based on dynamic model[J]. Acta Electronica Sinica, 2021, 49(4): 781–787. doi: 10.12263/DZXB.20200336 [2] 穆森, 李京华, 张恒, 等. 基于谐波集检测的飞行目标水下声探测算法研究[J]. 兵工学报, 2019, 40(5): 1050–1057. doi: 10.3969/j.issn.1000-1093.2019.05.018MU Sen, LI Jinghua, ZHANG Heng, et al. Research on underwater acoustic detection algorithm of aerial targets based on harmonic set detection[J]. Acta Armamentarii, 2019, 40(5): 1050–1057. doi: 10.3969/j.issn.1000-1093.2019.05.018 [3] PENHALE M and BARNARD A. Direction of arrival estimation in practical scenarios using moving standard deviation processing for localization and tracking with acoustic vector sensors[J]. Applied Acoustics, 2020, 168: 107421. doi: 10.1016/j.apacoust.2020.107421 [4] BUCKINGHAM M J, GIDDENS E M, POMPA J B, et al. Sound from a light aircraft for underwater acoustics experiments?[J]. Acta Acustica United with Acustica, 2002, 88(5): 752–755. [5] BUCKINGHAM M J, GIDDENS E M, SIMONET F, et al. Propeller noise from a light aircraft for low-frequency measurements of the speed of sound in a marine sediment[J]. Journal of Computational Acoustics, 2002, 10(4): 445–464. doi: 10.1142/S0218396X02001760 [6] FERGUSON B G. A ground-based narrow-band passive acoustic technique for estimating the altitude and speed of a propeller-driven aircraft[J]. The Journal of the Acoustical Society of America, 1992, 92(3): 1403–1407. doi: 10.1121/1.403934 [7] 陈韶华, 陈川, 郑伟. 单矢量水听器线谱多目标分辨研究[J]. 电子与信息学报, 2010, 32(5): 1253–1256. doi: 10.3724/SP.J.1146.2009.00460CHEN Shaohua, CHEN Chuan, and ZHENG Wei. Multi-sources distinguishing by exploring line spectra with single acoustic vector sensor[J]. Journal of Electronics &Information Technology, 2010, 32(5): 1253–1256. doi: 10.3724/SP.J.1146.2009.00460 [8] 王彪, 陈宇, 徐千驰, 等. 非理想条件下基于矢量水听器阵列的一种快速方位估计算法[J]. 电子与信息学报, 2021, 43(3): 745–751. doi: 10.11999/JEIT200541WANG Biao, CHEN Yu, XU Qianchi, et al. A fast direction estimation algorithm based on vector hydrophone array under non-ideal conditions[J]. Journal of Electronics &Information Technology, 2021, 43(3): 745–751. doi: 10.11999/JEIT200541 [9] LO K W and FERGUSON B G. Broadband passive acoustic technique for target motion parameter estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(1): 163–175. doi: 10.1109/7.826319 [10] LO K W. Flight parameter estimation using instantaneous frequency and direction of arrival measurements from a single acoustic sensor node[J]. The Journal of the Acoustical Society of America, 2017, 141(3): 1332–1348. doi: 10.1121/1.4976091 [11] 刘凯悦, 彭朝晖, 张灵珊, 等. 水下水平阵对空中运动声源的线谱探测[J]. 声学学报, 2019, 44(4): 566–575. doi: 10.15949/j.cnki.0371-0025.2019.04.017LIU Kaiyue, PENG Zhaohui, ZHANG Lingshan, et al. Line spectrum detection of airborne moving source by underwater horizontal array[J]. Acta Acustica, 2019, 44(4): 566–575. doi: 10.15949/j.cnki.0371-0025.2019.04.017 [12] 安春莲, 杨古月, 杨延菊. 基于中值滤波预处理的强冲击噪声背景测向方法[J]. 电子学报, 2021, 49(6): 1159–1166. doi: 10.12263/DZXB.20200392AN Chunlian, YANG Guyue, and YANG Yanju. DOA estimation under strong impulsive noise based on median value filtering[J]. Acta Electronica Sinica, 2021, 49(6): 1159–1166. doi: 10.12263/DZXB.20200392 [13] URICK R J. Noise signature of an aircraft in level flight over a hydrophone in the sea[J]. The Journal of the Acoustical Society of America, 1972, 52(1A): 172. doi: 10.1121/1.1982074 [14] FERGUSON B G, CULVER R L, and GEMBA K L. International student challenge problem in acoustic signal processing 2019[J]. Acoustics Today, 2019, 15(1): 71–73. doi: 10.1121/AT.2019.15.1.73 [15] DIPASSIO III J. Tre DiPassio’s solution to the 2019 international student challenge problem in acoustic signal processing[EB/OL]. https://static1.squarespace.com/static/5d362ec264480900010504be/t/5d765d6527a38b3a5d5be508/1568038249817/TreDiPassio_ChallengeProblem2019Solution.pdf, 2019. [16] SUN Weitao, WANG Huigang, GU Qingyue, et al. Exact frequency estimation in the i. i. d. noise via KL divergence of accumulated power[J]. IEEE Communications Letters, 2021, 25(8): 2574–2578. doi: 10.1109/LCOMM.2021.3077315 [17] SUN Weitao, WANG Huigang, GU Qingyue, et al. Exact and robust time-frequency estimation via accumulation of phase-difference power on multiple log-sum[EB/OL]. https://doi.org/10.13140/RG.2.2.21036.59523, 2021. [18] SADEGHI M, BEHNIA F, and AMIRI R. Window selection of the Savitzky-Golay filters for signal recovery from noisy measurements[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(8): 5418–5427. doi: 10.1109/TIM.2020.2966310 -





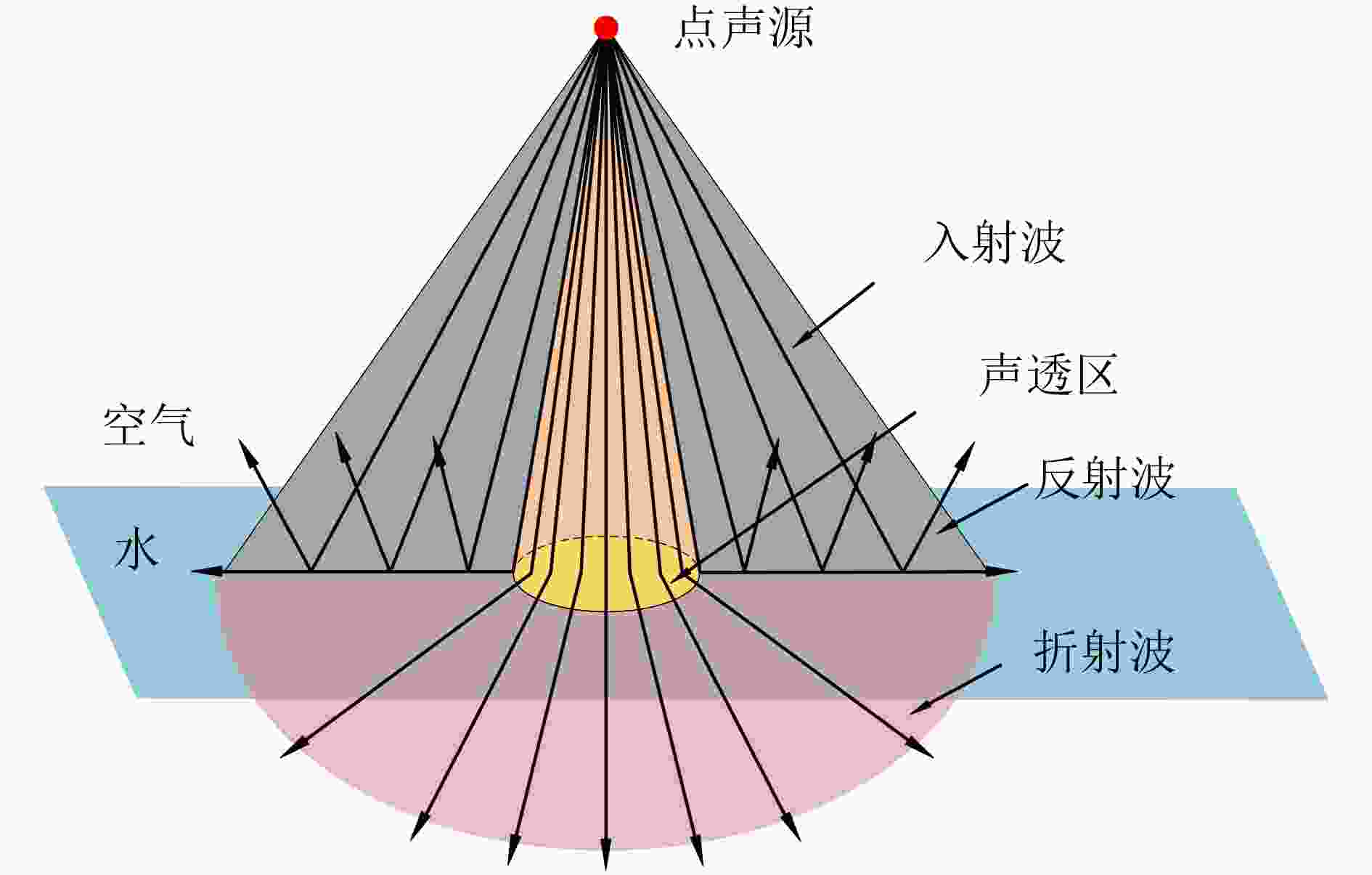
 下载:
下载:
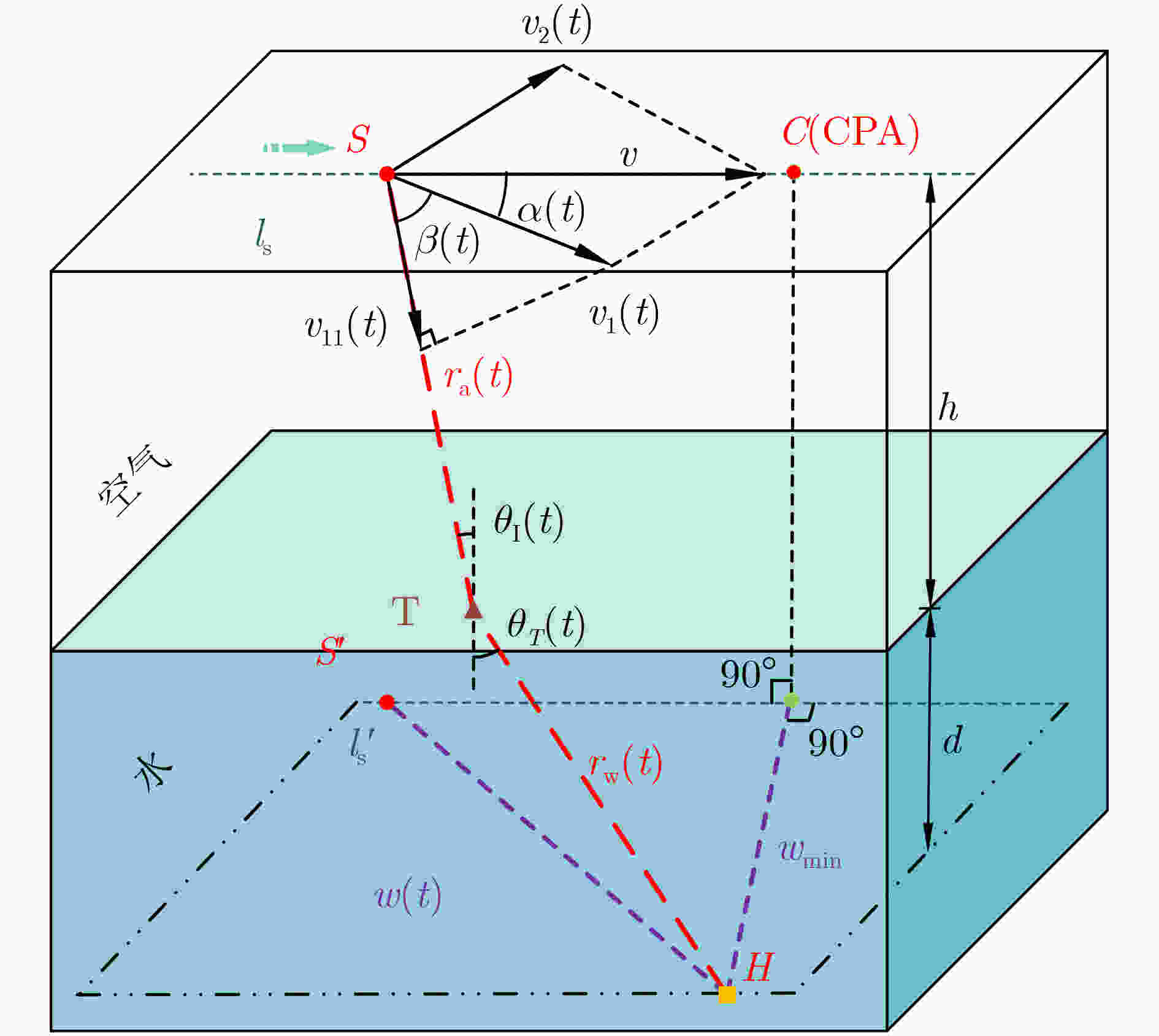
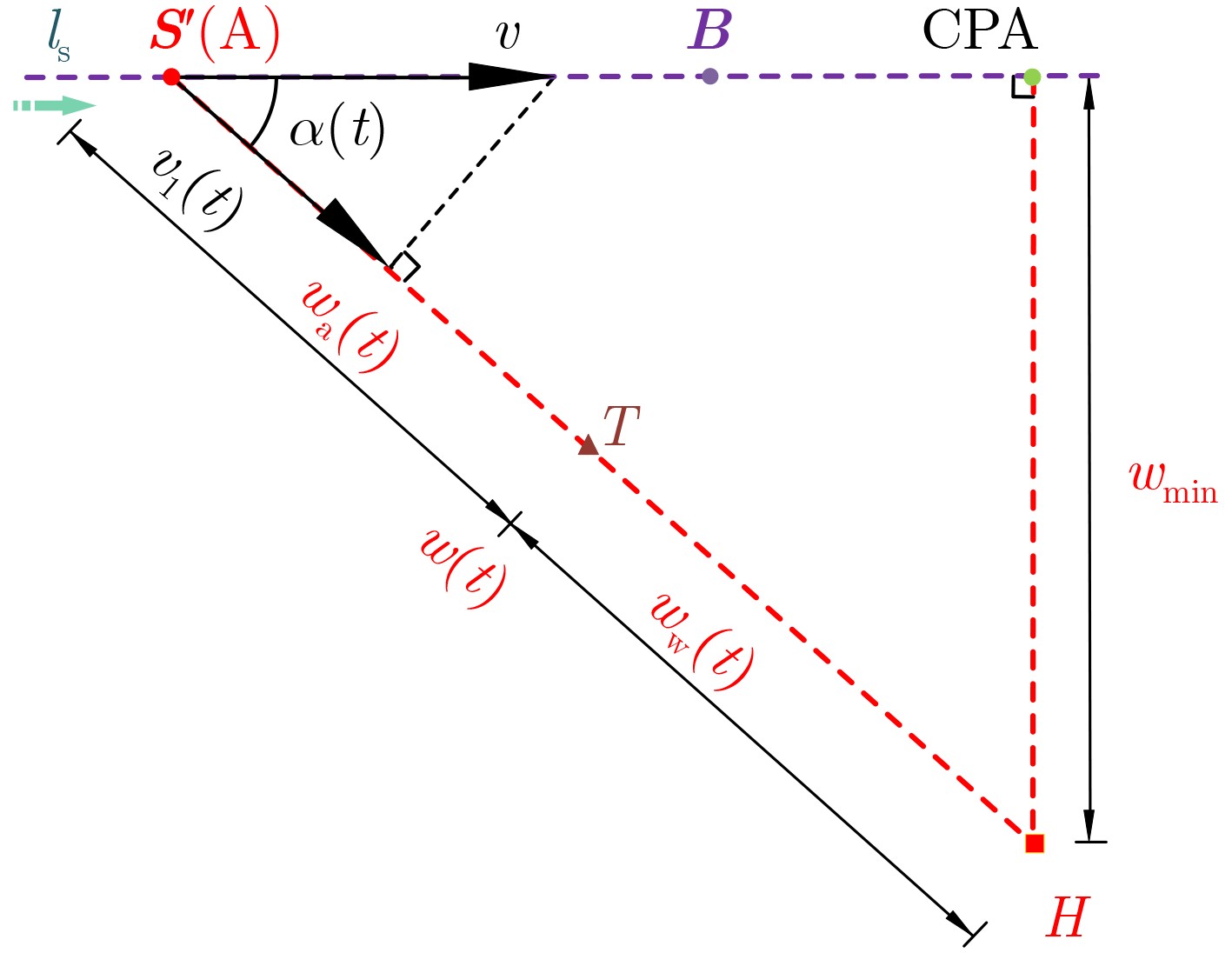
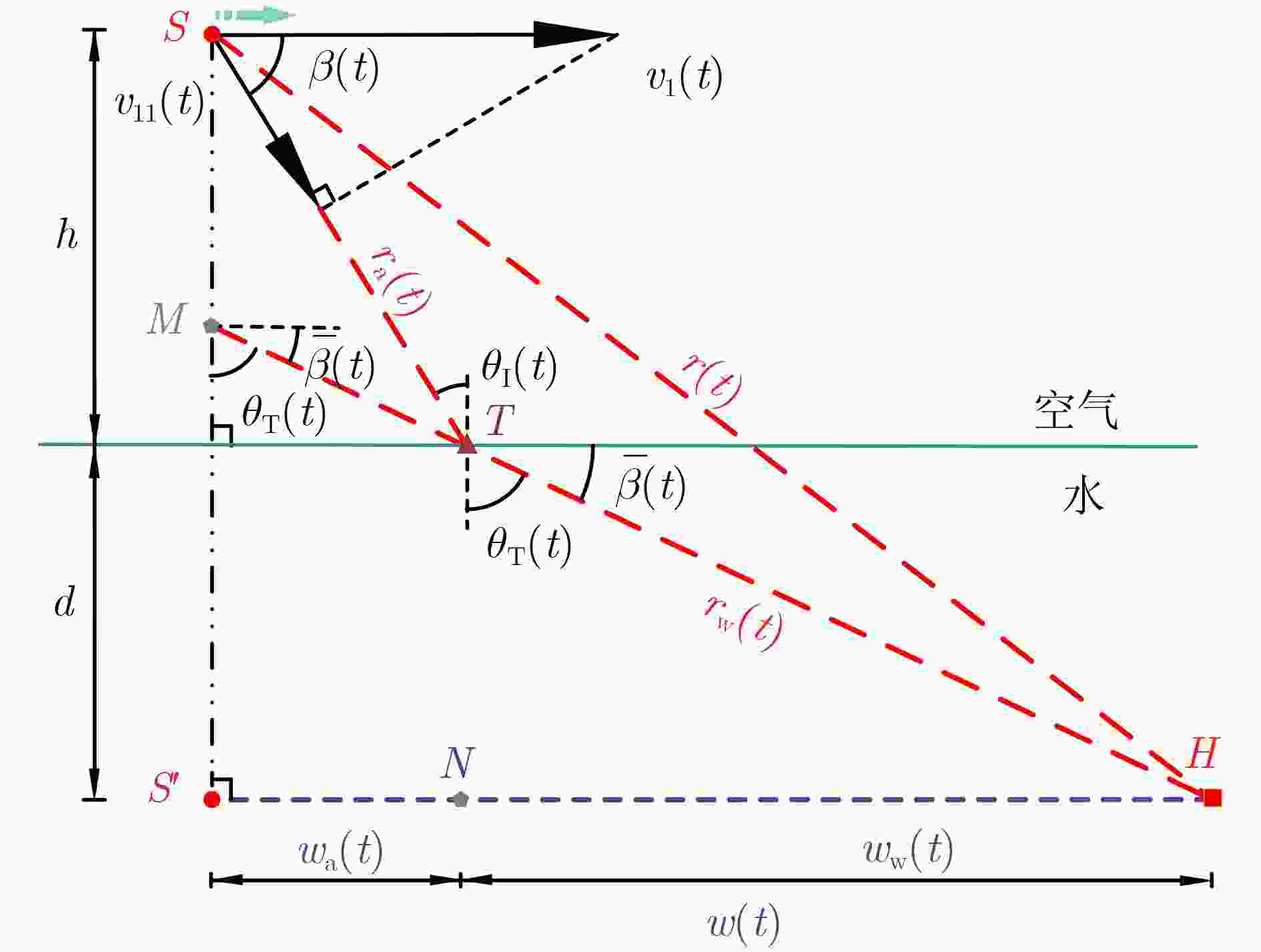


 下载:
下载:
