多方隐私集合交集计算技术综述

高莹; 王玮

doi:10.11999/JEIT220664

多方隐私集合交集计算技术综述

doi: 10.11999/JEIT220664

高莹^{1, 2, 3, ,},
王玮¹

1.
北京航空航天大学网络空间安全学院北京 100191
2.
中关村实验室北京 100094
3.
空天网络安全工业和信息化部重点实验室北京 100191

基金项目: 国家自然科学基金(61932011, 61972017)，北京市自然科学基金(M21033)

详细信息

作者简介:
高莹：女，副教授，研究方向为隐私计算与密码学应用

王玮：女，硕士生，研究方向为多方隐私集合交集计算

通讯作者:
高莹　gaoying@buaa.edu.cn

中图分类号: TN918; TP309.2
计量
- 文章访问数: 2015
- HTML全文浏览量: 1396
- PDF下载量: 613
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-23
- 修回日期: 2022-11-22
- 网络出版日期: 2022-11-25
- 刊出日期: 2023-05-10

A Survey of Multi-party Private Set Intersection

GAO Ying^{1, 2, 3
, ,},
WANG Wei¹

1.
School of Cyber Science and Technology, Beihang University, Beijing 100191, China
2.
Zhongguancun Laboratory, Beijing 100094, China
3.
Key Laboratory of Aerospace Network Security, Ministry of Industry and Information Technology, Beijing 100191, China

Funds: The National Natural Science Foundation of China (61932011, 61972017), The Natural Science Foundation of Beijing (M21033)

摘要

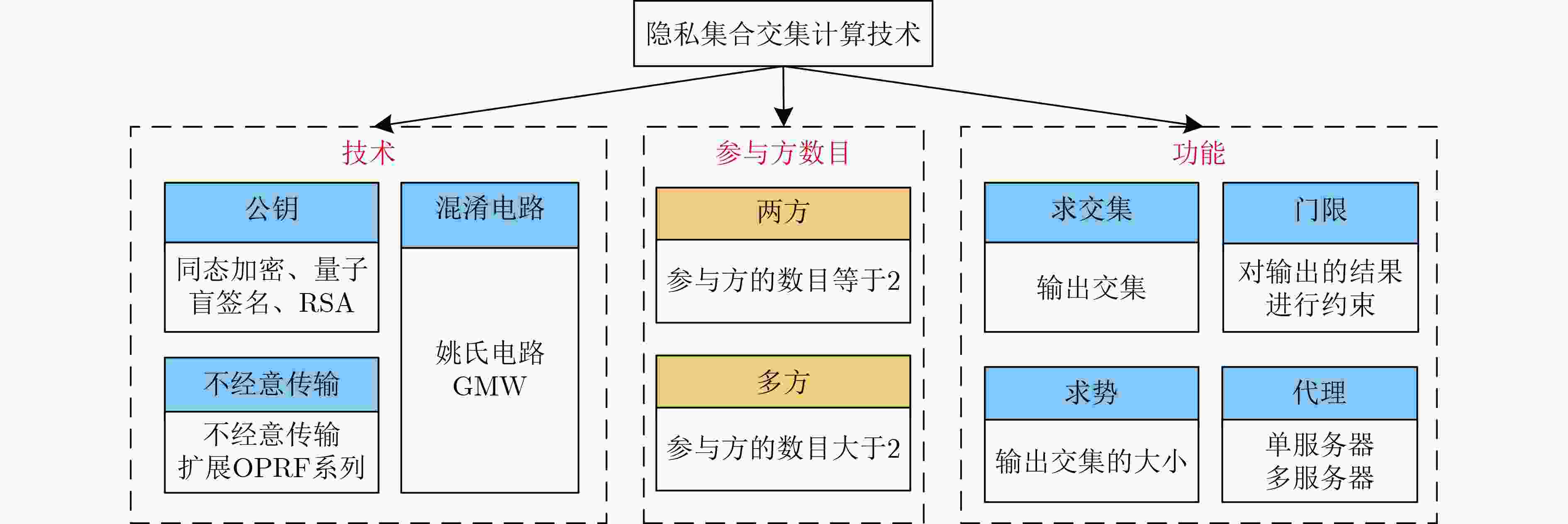
摘要: 随着互联网、大数据等新技术的快速发展，越来越多的分布式数据需要多方协作处理，隐私保护技术由此面临更大的挑战。安全多方计算是一种重要的隐私保护技术，可为数据的安全高效共享问题提供解决方案。作为安全多方计算的一个重要分支，隐私集合交集(PSI)计算技术可以在保护参与方的数据隐私性前提下计算两个或多个参与者私有数据集的交集，按照参与方数目可分为两方PSI和多方PSI。随着私人数据共享规模的扩大，多于两个参与方的应用场景越来越常见。多方PSI具有与两方PSI相似的技术基础但又有本质的不同。该文首先讨论了两方PSI的研究进展，其次详细梳理多方PSI技术的发展历程，将多方PSI技术依据应用场景的不同分为传统多方PSI技术以及门限多方PSI技术，并在不同场景下按照协议所采用密码技术和功能进行更细致的划分；对典型多方PSI协议进行分析，并对相关密码技术、敌手模型以及计算与通信复杂度进行对比。最后，给出了多方PSI技术的研究热点和未来发展方向。
- 隐私集合交集 /
- 不经意传输 /
- 不经意伪随机函数 /
- 加法同态加密 /
- 零秘密分享
Abstract: With the rapid development of new technologies, such as the Internet and big data, more and more distributed data need to be processed by multiple parties. Therefore, privacy protection technology is facing greater challenges. Secure multi-party computation is an important privacy protection technology, which can provide solutions for the secure and efficient sharing of data. As an important branch of secure multi-party computation, Private Set Intersection (PSI) technology can calculate the intersection of private data sets of two or more participants under the premise of protecting the data privacy of participants. It can be divided into two-party PSI and multi-party PSI according to the number of participants. With the expansion of private data sharing scale, application scenarios with more than two participants are more and more common. Multi party PSI has the same technical basis as the two party PSI, but has essential differences. Firstly, the research progress of the two-party PSI is discussed. Then the development processes of multi-party PSI are analyzed in detail. The multi-party PSI is divided into traditional multi-party PSI and threshold multi-party PSI according to the different scenarios. At the same time, protocols in different scenarios are divided more carefully according to the different basic cryptographic protocols they used and their different functions. The typical protocols are analyzed, and the cryptographic protocols, security model, computation and communication complexity of the protocols are discussed. Finally, the research hotspots and future development directions of multi-party PSI are pointed out.
- Private Set Intersection (PSI) /
- Oblivious Transfer (OT) /
- Oblivious pseudorandom function /
- Additively homomorphic encryption /
- Zero secret sharing

HTML全文

图 1 隐私集合交集计算技术分类图

下载: 全尺寸图片幻灯片

图 2 通信结构分类图

下载: 全尺寸图片幻灯片

表 1 基于公钥的多方PSI协议比较

协议	安全性	抗勾结	通信复杂度		计算复杂度
协议	安全性	抗勾结	Leader	Client	Leader	Client
文献[37]	半诚实	√	$O\left( {{n^2}{m^2}\lambda } \right)$	$O\left( {{n^2}{m^2}\lambda } \right)$	$O\left( {{n^2}m + n\lambda {m^2}} \right)$	$O\left( {{n^2}m + n\lambda {m^2}} \right)$
文献[38]	半诚实	√	$O\left( {nm\lambda } \right)$	$O\left( {m\lambda } \right)$	$ O\left( {nm{{\log }_2}^{m\kappa }} \right) $	$O\left( {m\kappa } \right)$
文献[38]	恶意	√	$O\left( {\left( {{n^2} + nm{{\log }_2}^m} \right)\kappa } \right)$	$O\left( {\left( {n + m{{\log }_2}^m} \right)\kappa } \right)$	$O\left( {{m^2}} \right)$	$O\left( {{m^2}} \right)$
文献[39]	半诚实	√	$O\left( {dn{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {d{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( d \right)$	$O\left( d \right)$
文献[39]	半诚实	√	$O\left( {d\ell {{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {d{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( d \right)$	$O\left( d \right)$
文献[40]	半诚实	√	$O\left( {m\ell {{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {\lambda m{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( m \right)$	$O\left( {\lambda m} \right)$
文献[41]	半诚实	√	$O\left( {nd} \right)$	$O\left( d \right)$	$O\left( {nd} \right)$	$O\left( d \right)$
文献[41]	半诚实	√	$O\left( {nm} \right)$	$O\left( m \right)$	$O\left( {nmk} \right)$	$O\left( m \right)$
文献[44]	恶意	√	$O\left( {\ell {n^2}{m^2}\kappa } \right)$	$O\left( {\ell {n^2}{m^2}\kappa } \right)$	$O\left( {{\ell ^2}{m^2}{\kappa ^3}} \right)$	$O\left( {{\ell ^2}{m^2}{\kappa ^3}} \right)$
文献[45]	恶意	√	$O\left( {n{m^2}\kappa } \right)$	$O\left( {n{m^2}\kappa } \right)$	$O\left( {n{m^2}\kappa } \right)$	$O\left( {n{m^2}{\kappa ^3}} \right)$
文献[46]	UC	√	$O\left( {n{m^2}\kappa } \right)$	$O\left( {n{m^2}\kappa } \right)$	$O\left( {\ell {m^2}{\kappa ^3}} \right)$	$O\left( {\ell {m^2}{\kappa ^3}} \right)$
文献[47]	恶意	√	$O\left( {\lambda {n^2}m} \right)$	$O\left( {\lambda {n^2}m} \right)$	$O\left( {{n^2}m + nm\lambda } \right)$	$O\left( {{n^2}m + nm\lambda } \right)$
文献[48]	恶意	√	$O\left( {\left( {{n^2} + nm} \right)\kappa } \right)$	$O\left( {\left( {{n^2} + nm} \right)\kappa } \right)$	$O\left( {nm{{\log }_2}^m} \right)$	$O\left( {m{{\left( {{{\log }_2}^m} \right)}^2}} \right)$
文献[49]	恶意	√	$O\left( {{n^2}\kappa + nm\left( {\kappa + \lambda + {{\log }_2}^m} \right)} \right)$	$O\left( {m\left( {\kappa + \lambda + {{\log }_2}^m} \right)} \right)$	$O\left( {nm} \right)$	$O\left( m \right)$
注：在复杂度对比中，$n$为参与方数目，$w$为腐败方数目，$m$为集合大小，$\lambda $和$\kappa $分别为统计和计算安全参数，$k$为哈希函数的个数，$d$为域的大小，$\ell $为同态公钥加密系统的门限值，${\log _2}^{\left\| X \right\|}$为二进制密文$X$的大小。补充说明的是：任意腐败方数目$w$的最大值应小于总参与方数目。

下载: 导出CSV

表 2 基于OT的多方PSI协议比较

协议	安全性	抗勾结	通信复杂度		计算复杂度
协议	安全性	抗勾结	Leader	Client	Leader	Client
文献[51]	半诚实	√	$O\left( {nm\lambda } \right)$	$O\left( {mw\lambda } \right)$	$O\left( {n\kappa } \right)$	$O\left( {w\kappa } \right)$
文献[51]	增强的半诚实	√	$O\left( {nm\lambda } \right)$	$O\left( {m\lambda } \right)$	$O\left( {n\kappa } \right)$	$O\left( \kappa \right)$
文献[52]	半诚实	√	$O\left( {nm\kappa } \right)$	$O\left( {m\kappa k} \right)$	$O\left( {nm\kappa } \right)$	$O\left( {m\kappa k} \right)$
文献[53]	半诚实	√	$O\left( {nm\kappa k} \right)$	$O\left( {nm\kappa k} \right)$	$O\left( {nm\kappa k} \right)$	$O\left( {nm\kappa k} \right)$
文献[53]	增强的半诚实	√	$O\left( {m\kappa k{{\log }_2}^n} \right)$	$O\left( {m\kappa k{{\log }_2}^n} \right)$	$O\left( {nm\kappa k} \right)$	$O\left( {nm\kappa k} \right)$
文献[54]	恶意	√	$ O\left( {nm{\lambda ^2} + nm\lambda {{\log }_2}^{\left( {m\lambda } \right)}} \right) $	$ O\left( {nm{\lambda ^2} + nm\lambda {{\log }_2}^{\left( {m\lambda } \right)}} \right) $	$O\left( {nmk} \right)$	$O\left( {nmk} \right)$
文献[55]	恶意	√	$O\left( {nm{\kappa ^2} + nm\kappa {{\log }_2}^{\left( {m\kappa } \right)}} \right)$	$O\left( {m{\kappa ^2} + m\kappa {{\log }_2}^{\left( {m\kappa } \right)}} \right)$	$O\left( {nm\kappa } \right)$	$O\left( {nm\kappa } \right)$
文献[56]	恶意	×	$O\left( {\left( {m + n} \right)\kappa } \right)$	$O\left( {m\kappa } \right)$	$O\left( {nm\kappa } \right)$	$O\left( {m\kappa } \right)$
文献[56]	恶意	√	$O\left( {m\kappa \cdot \max \left\{ {w,n - w} \right\}} \right)$	$O\left( {m\kappa } \right)$	$O\left( {m\kappa \left( {n - w} \right)} \right)$	$O\left( {mw\kappa } \right)$
文献[57]	恶意	√	$O\left( {nm\kappa + {n^2}\lambda \kappa {{\log }_2}^m} \right)$	$O\left( {m\kappa + n\lambda \kappa {{\log }_2}^m} \right)$	$O\left( {nm\kappa + m{{\left( {{{\log }_2}^m} \right)}^2}} \right)$	$O\left( {m\kappa + m{{\left( {{{\log }_2}^m} \right)}^2}} \right)$
注：在复杂度对比中，$n$为参与方数目，$w$为腐败方数目，$m$为集合大小，$\lambda $和$\kappa $分别为统计和计算安全参数，$k$为哈希函数的个数，$d$为域的大小，$\ell $为同态公钥加密系统的门限值，${\log _2}^{\left\| X \right\|}$为二进制密文$X$的大小。补充说明的是：任意腐败方数目$w$的最大值应小于总参与方数目。

下载: 导出CSV

表 3 代理多方PSI协议比较表

协议	敌手模型		公平性	可验证	服务器数量
协议	服务器	客户端	公平性	可验证	服务器数量
文献[58]	半诚实、恶意	恶意	√	√	1
文献[59]	诚实	半诚实	√	×	1
文献[60]	诚实	半诚实	√	×	1
文献[61]	半诚实	半诚实	×	×	1
文献[62]	半诚实	半诚实	×	×	1
文献[63]	恶意	半诚实	×	√	1
文献[64]	半诚实	半诚实	×	×	1
文献[65]	半诚实	半诚实	×	×	1
文献[66]	半诚实、社会理性	社会理性	√	×	2
文献[67]	半诚实	半诚实	√	×	2
文献[68]	半诚实	半诚实	√	×	1

下载: 导出CSV

表 4 约束元素出现次数的门限多方PSI协议比较

协议	安全性	抗勾结	通信复杂度		计算复杂度
协议	安全性	抗勾结	Leader	Client	Leader	Client
文献[40]	半诚实	√	$O\left( {mn\ell {{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {\max \left( {\lambda ,n} \right)m{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {mn} \right)$	$O\left( {\max \left( {\lambda ,n} \right)m} \right)$
文献[59]	半诚实	×	$O\left( {\lambda {n^2}m{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {{n^2}m{{\log }_2}^{\left\| X \right\|}} \right)$	$O\left( {\lambda nm{{\log }_2}^{\left\| X \right\|}} \right)$	$ O\left( {\lambda nm} \right) $
文献[78]	半诚实	√	$O\left( {{n^3}m\lambda } \right)$	$O\left( {{n^3}m\lambda } \right)$	$O\left( {{t^4}{n^2}{m^2}} \right)$	$O\left( {{t^4}{n^2}{m^2}} \right)$
文献[79]	半诚实	√	$O\left( {nmtw} \right)$	$O\left( {nmtw} \right)$	$O\left( {m{{\left( {n{{\log }_2}^{{m \mathord{\left/ {\vphantom {m t}} \right. } t}}} \right)}^{2t}}} \right)$	$O\left( {m{{\left( {n{{\log }_2}^{{m \mathord{\left/ {\vphantom {m t}} \right. } t}}} \right)}^{2t}}} \right)$
文献[83]	半诚实	√	$O\left( {nm\left( {\lambda + \kappa + {{\log }_2}^m} \right)} \right)$	$O\left( {m\left( {\lambda + \kappa + {{\log }_2}^m} \right)} \right)$	$O\left( {nm\kappa } \right)$	$O\left( {m\kappa } \right)$
注：在复杂度对比中，$n$为参与方数目，$w$为腐败方数目，$t$为协议门限值，$m$为集合大小，$\lambda $和$\kappa $分别为统计和计算安全参数，$\ell $为同态公钥加密系统的门限值，${\log _2}^{\left\| X \right\|}$为二进制密文$X$的大小。补充说明的是：任意腐败方数目$w$的最大值应小于总参与方数目。

下载: 导出CSV

表 5 约束交集大小的门限多方PSI协议比较

协议	安全性	抗勾结	通信轮数	通信复杂度
文献[86]	半诚实	×	$O\left( n \right)$	$O\left( {{{\left( {nt} \right)}^2}} \right)$
文献[90]	半诚实	√	$O\left( 1 \right)$	$O\left( {nt \cdot {\text{poly}}\left( \lambda \right)} \right)$
文献[91]	半诚实	√	$O\left( 1 \right)$	$O\left( {n{t^2}\kappa \lambda } \right)$
注：在复杂度对比中，$n$为参与方数目，$t$为协议门限值，$\lambda $和$\kappa $分别为统计和计算安全参数。

下载: 导出CSV

参考文献(91)

[1]	HALLGREN P, ORLANDI C, and SABELFELD A. PrivatePool: Privacy-preserving ridesharing[C]. 2017 IEEE 30th Computer Security Foundations Symposium, Santa Barbara, USA, 2017: 276–291.
[2]	European Union. Regulation (EU) 2016/679 of the European parliament and of the council[R]. Brussels: European Union, 2016.
[3]	ZHAO Chuan, ZHAO Shengnan, ZHAO Minghao, et al. Secure multi-party computation: Theory, practice and applications[J]. Information Sciences, 2019, 476: 357–372. doi: 10.1016/j.ins.2018.10.024
[4]	MEADOWS C. A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party[C]. 1986 IEEE Symposium on Security and Privacy, Oakland, USA, 1986: 134–134.
[5]	HUBERMAN B A, FRANKLIN M, and HOGG T. Enhancing privacy and trust in electronic communities[C]. The 1st ACM Conference on Electronic Commerce, Denver, USA, 1999: 78–86.
[6]	FREEDMAN M J, NISSIM K, and PINKAS B. Efficient private matching and set intersection[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 1–19.
[7]	DE CRISTOFARO E and TSUDIK G. Practical private set intersection protocols with linear complexity[C]. 14th International Conference on Financial Cryptography and Data Security, Tenerife, Spain, 2010: 143–159.
[8]	FREEDMAN M J, HAZAY C, NISSIM K, et al. Efficient set intersection with simulation-based security[J]. Journal of Cryptology, 2016, 29(1): 115–155. doi: 10.1007/s00145-014-9190-0
[9]	窦家维, 刘旭红, 周素芳, 等. 高效的集合安全多方计算协议及应用[J]. 计算机学报, 2018, 41(8): 1844–1860. doi: 10.11897/SP.J.1016.2018.01844 DOU Jiawei, LIU Xuhong, ZHOU Sufang, et al. Efficient secure multiparty set operations protocols and their application[J]. Chinese Journal of Computers, 2018, 41(8): 1844–1860. doi: 10.11897/SP.J.1016.2018.01844
[10]	周素芳, 李顺东, 郭奕旻, 等. 保密集合相交问题的高效计算[J]. 计算机学报, 2018, 41(2): 464–480. doi: 10.11897/SP.J.1016.2018.00464 ZHOU Sufang, LI Shundong, GUO Yimin, et al. Efficient secure set intersection problem computation[J]. Chinese Journal of Computers, 2018, 41(2): 464–480. doi: 10.11897/SP.J.1016.2018.00464
[11]	唐春明, 林旭慧. 隐私保护集合交集计算协议[J]. 信息网络安全, 2020, 20(1): 9–15. doi: 10.3969/j.issn.1671-1122.2020.01.002 TANG Chunming and LIN Xuhui. Protocol of privacy-preserving set intersection computation[J]. Netinfo Security, 2020, 20(1): 9–15. doi: 10.3969/j.issn.1671-1122.2020.01.002
[12]	HUANG Yan, EVANS D, and KATZ J. Private set intersection: Are garbled circuits better than custom protocols?[C]. 19th Annual Network and Distributed System Security Symposium, San Diego, USA, 2012.
[13]	PINKAS B, SCHNEIDER T, SEGEV G, et al. Phasing: Private set intersection using permutation-based hashing[C]. The 24th USENIX Conference on Security Symposium, Washington, USA, 2015: 515–530.
[14]	PINKAS B, SCHNEIDER T, WEINERT C, et al. Efficient circuit-based PSI via cuckoo hashing[C]. 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 2018: 125–157.
[15]	PINKAS B, SCHNEIDER T, TKACHENKO O, et al. Efficient circuit-based PSI with linear communication[C]. 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 2019: 122–153.
[16]	CHANDRAN N, GUPTA D, and SHAH A. Circuit-PSI with linear complexity via relaxed batch OPPRF[J]. Proceedings on Privacy Enhancing Technologies, 2022, 2022(1): 353–372. doi: 10.2478/popets-2022-0018
[17]	DONG Changyu, CHEN Liqun, and WEN Zikai. When private set intersection meets big data: An efficient and scalable protocol[C]. The 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 2013: 789–800.
[18]	PINKAS B, SCHNEIDER T, and ZOHNER M. Faster private set intersection based on OT extension[C]. The 23rd USENIX Conference on Security Symposium, San Diego, USA, 2014: 797–812.
[19]	KOLESNIKOV V, KUMARESAN R, ROSULEK M, et al. Efficient batched oblivious PRF with applications to private set intersection[C]. The 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 2016: 818–829.
[20]	ORRÙ M, ORSINI E, and SCHOLL P. Actively secure 1-out-of-N OT extension with application to private set intersection[C]. Cryptographers’ Track at the RSA Conference 2017, San Francisco, USA, 2017: 381–396.
[21]	RINDAL P and ROSULEK M. Improved private set intersection against malicious adversaries[C]. 36th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 2017: 235–259.
[22]	RINDAL P and ROSULEK M. Malicious-secure private set intersection via dual execution[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 1229–1242.
[23]	PINKAS B, SCHNEIDER T, and ZOHNER M. Scalable private set intersection based on OT extension[J]. ACM Transactions on Privacy and Security, 2018, 21(2): 7. doi: 10.1145/3154794
[24]	PINKAS B, ROSULEK M, TRIEU N, et al. SpOT-light: Lightweight private set intersection from sparse OT extension[C]. 39th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2019: 401–431.
[25]	PINKAS B, ROSULEK M, TRIEU N, et al. PSI from PaXoS: Fast, malicious private set intersection[C]. 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques on Advances in Cryptology, Zagreb, Croatia, 2020: 739–767.
[26]	CHASE M and MIAO Peihan. Private set intersection in the internet setting from lightweight oblivious PRF[C]. 40th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2020: 34–63.
[27]	RINDAL P and SCHOPPMANN P. VOLE-PSI: Fast OPRF and circuit-PSI from vector-OLE[C]. 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques on Advances in Cryptology, Zagreb, Croatia, 2021: 901–930.
[28]	程楠, 赵运磊. 一种高效的关于两方集合并/交集基数的隐私计算方法[J]. 密码学报, 2021, 8(2): 352–364. doi: 10.13868/j.cnki.jcr.000443 CHENG Nan and ZHAO Yunlei. Efficient approach regarding two-party privacy-preserving set union/intersection cardinality[J]. Journal of Cryptologic Research, 2021, 8(2): 352–364. doi: 10.13868/j.cnki.jcr.000443
[29]	申立艳, 陈小军, 时金桥, 等. 隐私保护集合交集计算技术研究综述[J]. 计算机研究与发展, 2017, 54(10): 2153–2169. doi: 10.7544/issn1000-1239.2017.20170461 SHEN Liyan, CHEN Xiaojun, SHI Jinqiao, et al. Survey on private preserving set intersection technology[J]. Journal of Computer Research and Development, 2017, 54(10): 2153–2169. doi: 10.7544/issn1000-1239.2017.20170461
[30]	崔泓睿, 刘天怡, 郁昱. 带隐私保护的集合交集计算协议的发展现状综述[J]. 信息安全与通信保密, 2019(3): 48–67. doi: 10.3969/j.issn.1009-8054.2019.03.010 CUI Hongrui, LIU Tianyi, and YU Yu. A survey on private set intersection[J]. Information Security and Communications Privacy, 2019(3): 48–67. doi: 10.3969/j.issn.1009-8054.2019.03.010
[31]	魏立斐, 刘纪海, 张蕾, 等. 面向隐私保护的集合交集计算综述[J]. 计算机研究与发展, 2022, 59(8): 1782–1799. doi: 10.7544/issn1000-1239.20210685 WEI Lifei, LIU Jihai, ZHANG Lei, et al. Survey of privacy preserving oriented set intersection computation[J]. Journal of Computer Research and Development, 2022, 59(8): 1782–1799. doi: 10.7544/issn1000-1239.20210685
[32]	黄翠婷, 张帆, 孙小超, 等. 隐私集合求交技术的理论与金融实践综述[J]. 信息通信技术与政策, 2021, 47(6): 50–56. doi: 10.12267/j.issn.2096-5931.2021.06.006 HUANG Cuiting, ZHANG Fan, SUN Xiaochao, et al. A survey of private set intersection technology and finance practice[J]. Information and Communications Technology and Policy, 2021, 47(6): 50–56. doi: 10.12267/j.issn.2096-5931.2021.06.006
[33]	RABIN M O. How to exchange secrets with oblivious transfer[R]. Cambridge: Harvard University, 2005.
[34]	ISHAI Y, KILIAN J, NISSIM K, et al. Extending oblivious transfers efficiently[C]. 23rd Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2003: 145–161.
[35]	KOLESNIKOV V and KUMARESAN R. Improved OT extension for transferring short secrets[C]. 33rd Annual Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2013: 54–70.
[36]	YANG Kang, WENG Chenkai, LAN Xiao, et al. Ferret: Fast extension for correlated OT with small communication[C/OL]. The 2020 ACM SIGSAC Conference on Computer and Communications Security, 2020: 1607–1626.
[37]	KISSNER L and SONG D. Privacy-preserving set operations[C]. 25th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2005: 241–257.
[38]	HAZAY C and VENKITASUBRAMANIAM M. Scalable multi-party private set-intersection[C]. 20th IACR International Conference on Practice and Theory in Public-Key Cryptography, Amsterdam, The Netherlands, 2017: 175–203.
[39]	BAY A, ERKIN Z, ALISHAHI M, et al. Multi-party private set intersection protocols for practical applications[C/OL]. The 18th International Conference on Security and Cryptography, 2021: 515–522.
[40]	BAY A, ERKIN Z, HOEPMAN J H, et al. Practical multi-party private set intersection protocols[J]. IEEE Transactions on Information Forensics and Security, 2022, 17: 1–15. doi: 10.1109/TIFS.2021.3118879
[41]	VOS J, CONTI M, and ERKIN Z. Fast multi-party private set operations in the star topology from secure ANDs and ORs[EB/OL].https://eprint.iacr.org/2022/721, 2022.
[42]	张蕾, 贺崇德, 魏立斐. 高效且恶意安全的三方小集合隐私交集计算协议[J]. 计算机研究与发展, 2022, 59(10): 2286–2298. doi: 10.7544/issn1000-1239.20220471 ZHANG Lei, HE Chongde, and WEI Lifei. Efficient and malicious secure three-party private set intersection computation protocols for small sets[J]. Journal of Computer Research and Development, 2022, 59(10): 2286–2298. doi: 10.7544/issn1000-1239.20220471
[43]	LI Ronghua and WU Chuankun. An unconditionally secure protocol for multi-party set intersection[C]. 5th International Conference on Applied Cryptography and Network Security, Zhuhai, China, 2007: 226–236.
[44]	SANG Yingpeng and SHEN Hong. Privacy preserving set intersection protocol secure against malicious behaviors[C]. Eighth International Conference on Parallel and Distributed Computing, Applications and Technologies, Adelaide, Australia, 2007: 461–468.
[45]	SANG Yingpeng and SHEN Hong. Privacy preserving set intersection based on bilinear groups[C]. The Thirty-First Australasian Conference on Computer Science, Wollongong, Australia, 2008: 47–54.
[46]	SANG Yingpeng and SHEN Hong. Efficient and secure protocols for privacy-preserving set operations[J]. ACM Transactions on Information and System Security, 2009, 13(1): 9. doi: 10.1145/1609956.1609965
[47]	CHEON J H, JARECKI S, and SEO J H. Multi-party privacy-preserving set intersection with quasi-linear complexity[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2012, E95.A(8): 1366–1378. doi: 10.1587/transfun.E95.A.1366
[48]	GHOSH S and NILGES T. An algebraic approach to maliciously secure private set intersection[C]. 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 2019: 154–185.
[49]	QIU Zhi, YANG Kang, YU Yu, et al. Maliciously secure multi-party PSI with lower bandwidth and faster computation[C]. 24th International Conference on Information and Communications Security, Canterbury, UK, 2022: 69–88.
[50]	DEBNATH S K, CHOUDHURY T, KUNDU N, et al. Post-quantum secure multi-party private set-intersection in star network topology[J]. Journal of Information Security and Applications, 2021, 58: 102731. doi: 10.1016/j.jisa.2020.102731
[51]	KOLESNIKOV V, MATANIA N, PINKAS B, et al. Practical multi-party private set intersection from symmetric-key techniques[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 1257–1272.
[52]	KAVOUSI A, MOHAJERI J, and SALMASIZADEH M. Efficient scalable multi-party private set intersection using oblivious PRF[C]. 17th International Workshop on Security and Trust Management, Darmstadt, Germany, 2021: 81–99.
[53]	INBAR R, OMRI E, and PINKAS B. Efficient scalable multiparty private set-intersection via garbled bloom filters[C]. 11th International Conference on Security and Cryptography for Networks, Amalfi, Italy, 2018: 235–252.
[54]	ZHANG En, LIU Fenghao, LAI Qiqi, et al. Efficient multi-party private set intersection against malicious adversaries[C]. The 2019 ACM SIGSAC Conference on Cloud Computing Security Workshop, London, England, 2019: 93–104.
[55]	BEN-EFRAIM A, NISSENBAUM O, OMRI E, et al. PSImple: Practical multiparty maliciously-secure private set intersection[C]. The 2022 ACM on Asia Conference on Computer and Communications Security, Nagasaki, Japan, 2022: 1098–1112.
[56]	NEVO O, TRIEU N, and YANAI A. Simple, fast malicious multiparty private set intersection[C]. The 2021 ACM SIGSAC Conference on Computer and Communications Security, Seoul, Korea, 2021: 1151–1165.
[57]	GORDON S D, HAZAY C, and LE P H. Fully secure PSI via MPC-in-the-head[EB/OL]. https://eprint.iacr.org/2022/379, 2022.
[58]	KAMARA S, MOHASSEL P, RAYKOVA M, et al. Scaling private set intersection to billion-element sets[C]. 18th International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 2014: 195–215.
[59]	MIYAJI A and NISHIDA S. A scalable multiparty private set intersection[C]. 9th International Conference on Network and System Security, New York, USA, 2015: 376–385.
[60]	ZHU Hongliang, CHEN Meiqi, SUN Maohua, et al. Outsourcing set intersection computation based on bloom filter for privacy preservation in multimedia processing[J]. Security and Communication Networks, 2018, 2018: 5841967. doi: 10.1155/2018/5841967
[61]	王勤, 魏立斐, 刘纪海, 等. 基于云服务器辅助的多方隐私交集计算协议[J]. 计算机科学, 2021, 48(10): 301–307. doi: 10.11896/jsjkx.210300308 WANG Qin, WEI Lifei, LIU Jihai, et al. Private set intersection protocols among multi-party with cloud server aided[J]. Computer Science, 2021, 48(10): 301–307. doi: 10.11896/jsjkx.210300308
[62]	ABADI A, TERZIS S, and DONG Changyu. O-PSI: Delegated private set intersection on outsourced datasets[C]. 30th IFIP TC 11 International Conference on ICT Systems Security and Privacy Protection, Hamburg, Germany, 2015: 3–17.
[63]	ABADI A, TERZIS S, and DONG Changyu. VD-PSI: Verifiable delegated private set intersection on outsourced private datasets[C]. 20th International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 2016: 149–168.
[64]	ABADI A, TERZIS S, METERE R, et al. Efficient delegated private set intersection on outsourced private datasets[J]. IEEE Transactions on Dependable and Secure Computing, 2019, 16(4): 608–624. doi: 10.1109/TDSC.2017.2708710
[65]	ABADI A, DONG Changyu, MURDOCH S J, et al. Multi-party updatable delegated private set intersection[C]. 26th International Conference on Financial Cryptography and Data Security, Grenada, Grenada, 2022: 100–119.
[66]	ZHANG En, LI Fenghua, NIU Ben, et al. Server-aided private set intersection based on reputation[J]. Information Sciences, 2017, 387: 180–194. doi: 10.1016/j.ins.2016.09.056
[67]	张恩, 金刚刚. 基于同态加密和Bloom过滤器的云外包多方隐私集合比较协议[J]. 计算机应用, 2018, 38(8): 2256–2260. doi: 10.11772/j.issn.1001-9081.2018010075 ZHANG En and JIN Ganggang. Cloud outsourcing multiparty private set intersection protocol based on homomorphic encryption and Bloom filter[J]. Journal of Computer Applications, 2018, 38(8): 2256–2260. doi: 10.11772/j.issn.1001-9081.2018010075
[68]	MIYAJI A, NAKASHO K, and NISHIDA S. Privacy-preserving integration of medical data[J]. Journal of Medical Systems, 2017, 41(3): 37. doi: 10.1007/s10916-016-0657-4
[69]	HU Keji and ZHANG Wensheng. mPSI: Many-to-one private set intersection[C]. 2017 IEEE 4th International Conference on Cyber Security and Cloud Computing, New York, USA, 2017: 187–192.
[70]	DEBNATH S K, STǍNICǍ P, KUNDU N, et al. Secure and efficient multiparty private set intersection cardinality[J]. Advances in Mathematics of Communications, 2021, 15(2): 365–386. doi: 10.3934/amc.2020071
[71]	SHI Runhua. Quantum multiparty privacy set intersection cardinality[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2021, 68(4): 1203–1207. doi: 10.1109/TCSII.2020.3032550
[72]	赵雪玲, 家珠亮, 李顺东. 集合交集问题的安全计算[J]. 密码学报, 2022, 9(2): 294–307. doi: 10.13868/j.cnki.jcr.000520 ZHAO Xueling, JIA Zhuliang, and LI Shundong. A secure multiparty intersection computation[J]. Journal of Cryptologic Research, 2022, 9(2): 294–307. doi: 10.13868/j.cnki.jcr.000520
[73]	TRIEU N, YANAI A, and GAO Jiahui. Multiparty private set intersection cardinality and its applications[EB/OL]. https://eprint.iacr.org/2022/735, 2022.
[74]	杨亚涛, 赵阳, 张卷美, 等. 同态密码理论与应用进展[J]. 电子与信息学报, 2021, 43(2): 475–487. doi: 10.11999/JEIT191019 YANG Yatao, ZHAO Yang, ZHANG Juanmei, et al. Recent development of theory and application on homomorphic encryption[J]. Journal of Electronics &Information Technology, 2021, 43(2): 475–487. doi: 10.11999/JEIT191019
[75]	DAVIDSON A and CID C. An efficient toolkit for computing private set operations[C]. 22nd Australasian Conference on Information Security and Privacy, Auckland, New Zealand, 2017: 261–278.
[76]	GARIMELLA G, PINKAS B, ROSULEK M, et al. Oblivious key-value stores and amplification for private set intersection[C/OL]. 41st Annual International Cryptology Conference on Advances in Cryptology, 2021: 395–425.
[77]	LU Linpeng and DING Ning. Multi-party private set intersection in vertical federated learning[C]. 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications, Guangzhou, China, 2020: 707–714.
[78]	KISSNER L and SONG D. Private and threshold set-intersection[R]. Pittsburgh: Carnegie Mellon University, 2004.
[79]	MAHDAVI R A, HUMPHRIES T, KACSMAR B, et al. Practical over-threshold multi-party private set intersection[C]. Annual Computer Security Applications Conference, Austin, USA, 2020: 772–783.
[80]	SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612–613. doi: 10.1145/359168.359176
[81]	PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes[C]. International Conference on the Theory and Application of Cryptographic Techniques, Prague, Czech Republic, 1999: 223–238.
[82]	KERSCHBAUM F, BISWAS D, and DE HOOGH S. Performance comparison of secure comparison protocols[C]. 2009 20th International Workshop on Database and Expert Systems Application, Linz, Austria, 2009: 133–136.
[83]	CHANDRAN N, DASGUPTA N, GUPTA D, et al. Efficient linear multiparty PSI and extensions to circuit/quorum PSI[C/OL]. The 2021 ACM SIGSAC Conference on Computer and Communications Security, 2021: 1182–1204.
[84]	ZHAO Yongjun and CHOW S S M. Are you the one to share? Secret transfer with access structure[J]. Proceedings on Privacy Enhancing Technologies, 2017, 2017(1): 149–169. doi: 10.1515/popets-2017-0010
[85]	ZHAO Yongjun and CHOW S S M. Can you find the one for me?[C]. The 2018 Workshop on Privacy in the Electronic Society, Toronto, Canada, 2018: 54–65.
[86]	GHOSH S and SIMKIN M. The communication complexity of threshold private set intersection[C]. 39th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2019: 3–29.
[87]	ZHANG En, CHANG Jian, and LI Yu. Efficient threshold private set intersection[J]. IEEE Access, 2021, 9: 6560–6570. doi: 10.1109/ACCESS.2020.3048743
[88]	ZHAO Shengnan, MA Ming, SONG Xiangfu, et al. Lightweight threshold private set intersection via oblivious transfer[C]. 16th International Conference on Wireless Algorithms, Systems, and Applications, Nanjing, China, 2021: 108–116.
[89]	BONEH D, GENNARO R, GOLDFEDER S, et al. Threshold cryptosystems from threshold fully homomorphic encryption[C]. 38th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2018: 565–596.
[90]	BADRINARAYANAN S, MIAO Peihan, RAGHURAMAN S, et al. Multi-party threshold private set intersection with sublinear communication[C/OL]. 24th IACR International Conference on Practice and Theory of Public Key Cryptography, 2021: 349–379.
[91]	BRANCO P, DÖTTLING N, and PU Sihang. Multiparty cardinality testing for threshold private intersection[C/OL]. 24th IACR International Conference on Practice and Theory of Public Key Cryptography, 2021: 32–60.