Transfer Fuzzy C-Means Clustering Based on Maximum Mean Discrepancy
-
摘要: 该文针对迁移聚类问题,提出一种基于最大平均差异的迁移模糊C均值(TFCM-MMD)聚类算法。TFCM-MMD解决了迁移模糊C均值聚类算法在源域与目标域数据分布差异大的情况下迁移学习效果减弱的问题。 该算法基于最大平均差异准则度量域间差异,通过学习源域和目标域的投影矩阵,以减小源域和目标域数据在公共子空间分布的差异,进而提升迁移学习的效果。最后,通过基于合成数据集和医学图像分割数据集的实验,进一步验证了TFCM-MMD算法在解决域间差异大的迁移聚类问题上的有效性。Abstract: In this paper, a Transfer Fuzzy C-Means clustering algorithm based on Maximum Mean Discrepancy (TFCM-MMD) is proposed. TFCM-MMD solves the problem that the transfer learning effect of the transfer fuzzy C-means clustering algorithm is weakened when the data distribution between source domain and target domain is very different. The algorithm measures inter-domain differences based on the maximum mean discrepancy criterion, and reduces the differences of data distribution between source domain and target domain in the common subspace by learning the projection matrix of source domain and target domain, so as to improve the effect of transfer learning. Finally, experiments based on synthetic datasets and medical image segmentation datasets verify further the effectiveness of TFCM-MMD algorithm in solving transfer clustering problems with large inter-domain differences.
-
Key words:
- Transfer learning /
- Fuzzy clustering /
- Maximum Mean Discrepancy(MMD)
-
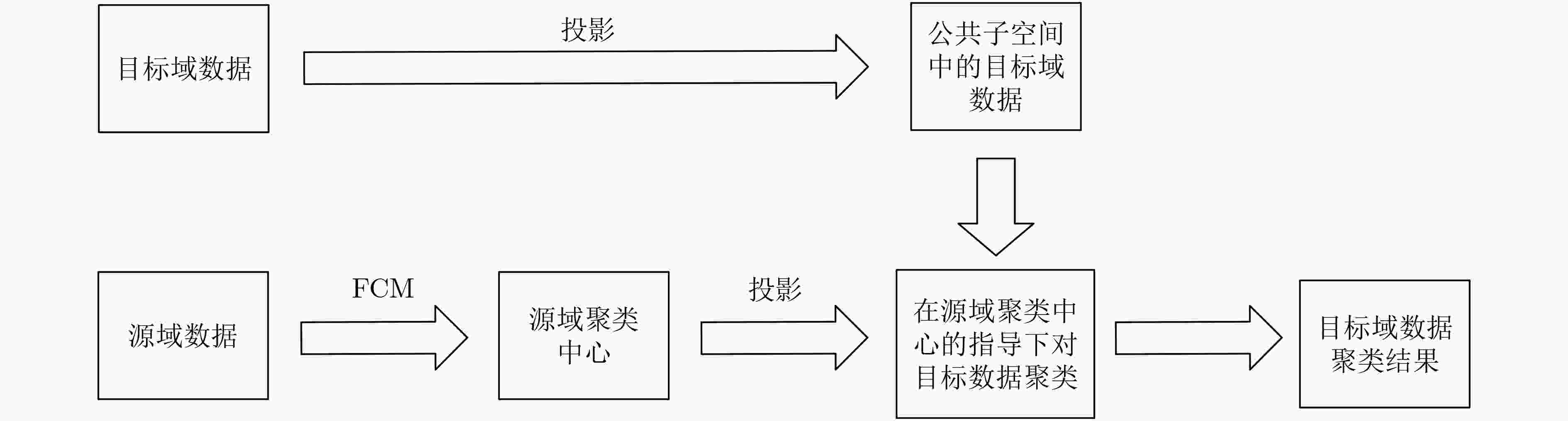
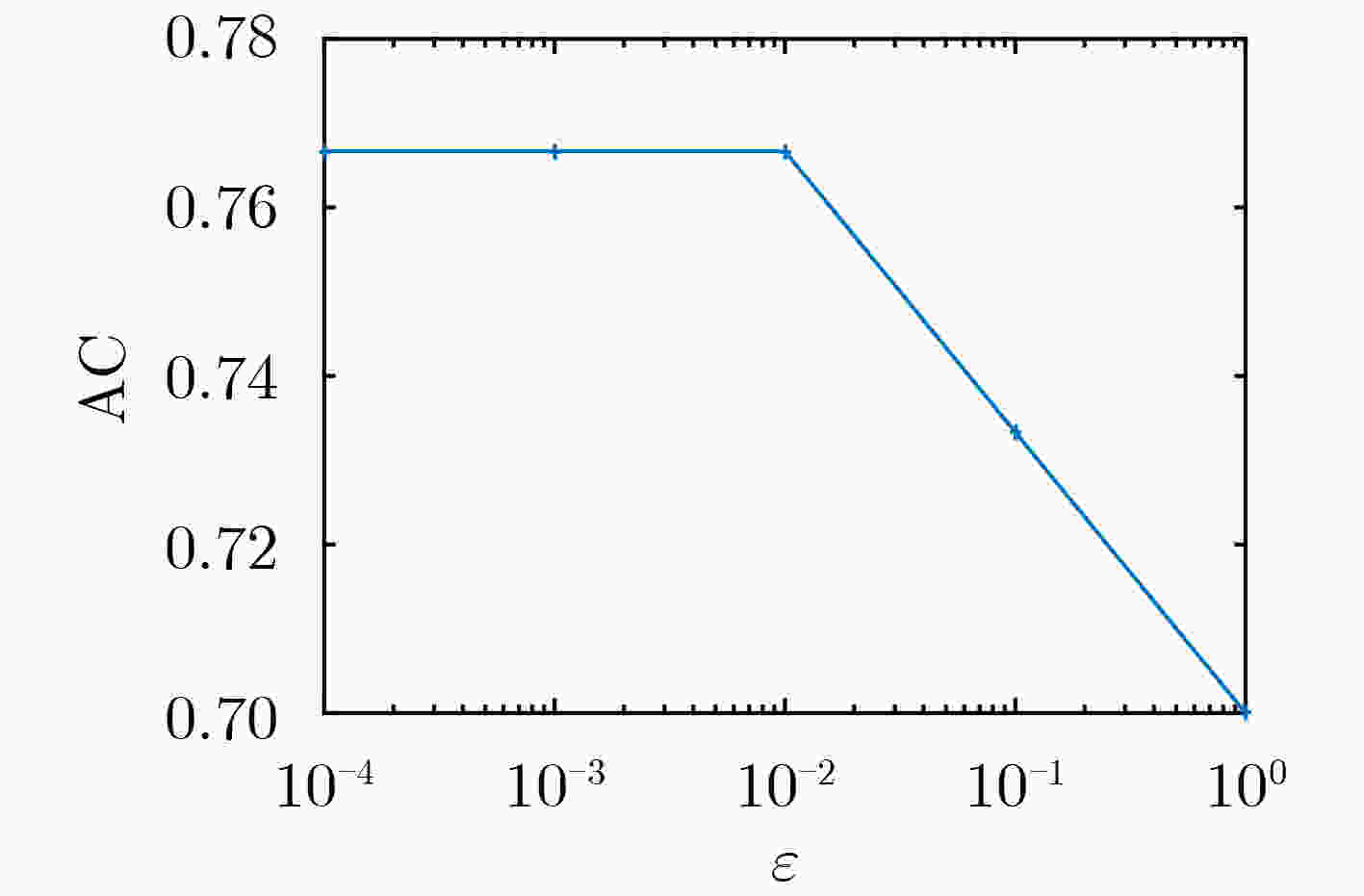
算法1 TFCM-MMD 输入:源域数据${{\boldsymbol{X}}_{\text{s} } }$, 目标域数据${{\boldsymbol{X}}_{\text{t} } }$,源域聚类数$ {C_{\text{s}}} $, 目标域聚类数$ {C_{\text{t}}} $,模糊加权系数$ {m_1} $, $ {m_2} $,迁移率λ,学习率η, 最大迭代次数nmax,
终止阈值$ \varepsilon $输出:目标域模糊隶属度矩阵${\boldsymbol{U}}$ (1) 根据源域聚类数$ {C_{\text{s}}} $, 利用FCM对源域数据${{\boldsymbol{X}}_{\text{s} } }$进行聚类, 获得源域的聚类中心${\tilde {\boldsymbol{V}}_k}$; (2) 根据目标域聚类数$ {C_{\text{t}}} $初始化模糊隶属度矩阵${\boldsymbol{U}}(0)$,聚类中心相关性矩阵${\boldsymbol{R}}(0)$,根据投影后矩阵的维数r初始化投影矩阵${\boldsymbol{H}}(0)$,迭代次
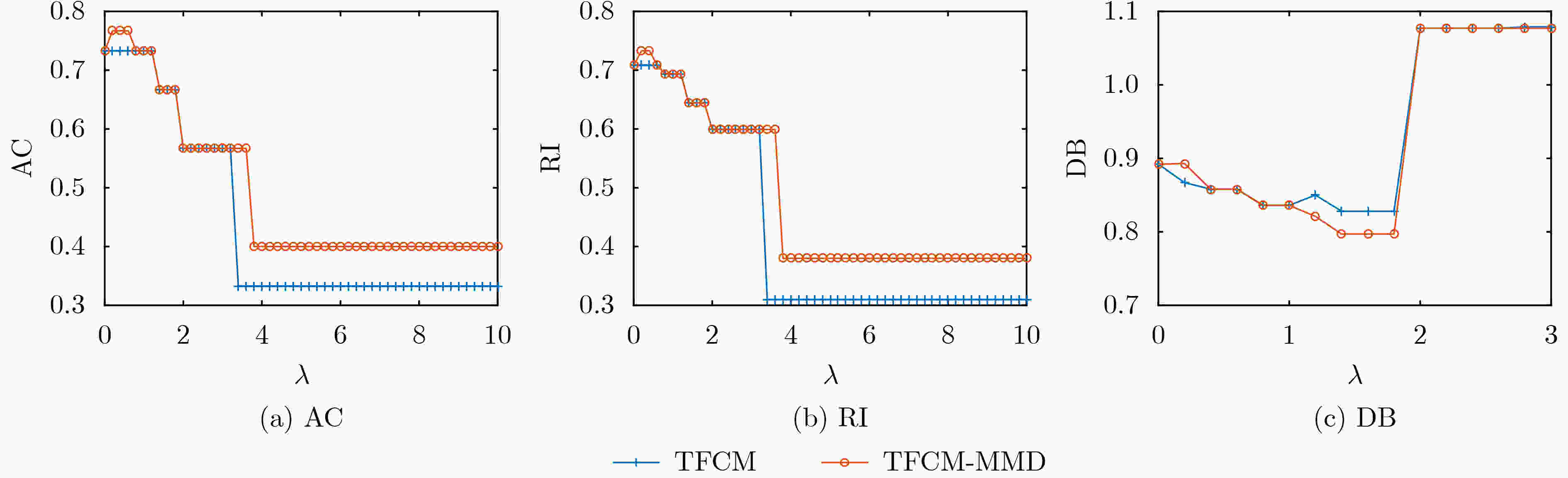
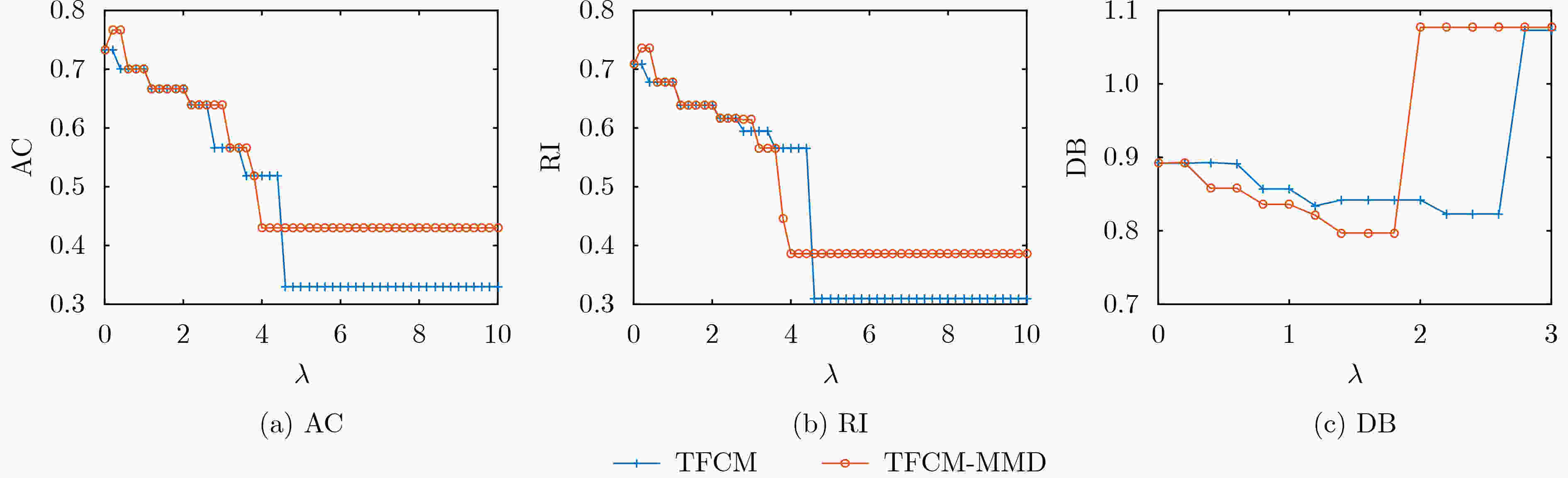
数t=0;(3) 重复; (4) t=t+1; (5) 利用式(7)计算聚类中心${\boldsymbol{V}}(t)$; (6) 利用式(8)计算模糊隶属度矩阵${\boldsymbol{U}}(t)$; (7) 利用式(9)计算聚类中心相关性矩阵${\boldsymbol{R}}(t)$; (8) 利用式(15)计算投影矩阵${\boldsymbol{H}}(t)$; (9) 直到$ |{J_{{\text{TFCM - MMD}}}}(t) - {J_{{\text{TFCM - MMD}}}}(t - 1)| < \varepsilon $或者 t>nmax 表 1 不同噪声水平下TFCM与TFCM-MMD抗负迁移性能比较(以AC为例)(%)
目标域数据 TFCM最差聚类结果 TFCM-MMD最差聚类结果 聚类性能提升 T2-1 69.86 70.36 0.5 T2-2 67.64 71.67 4.0 T2-3 61.21 67.40 6.2 表 2 FCM-MMD与TFCM-MMD聚类性能对比(AC)
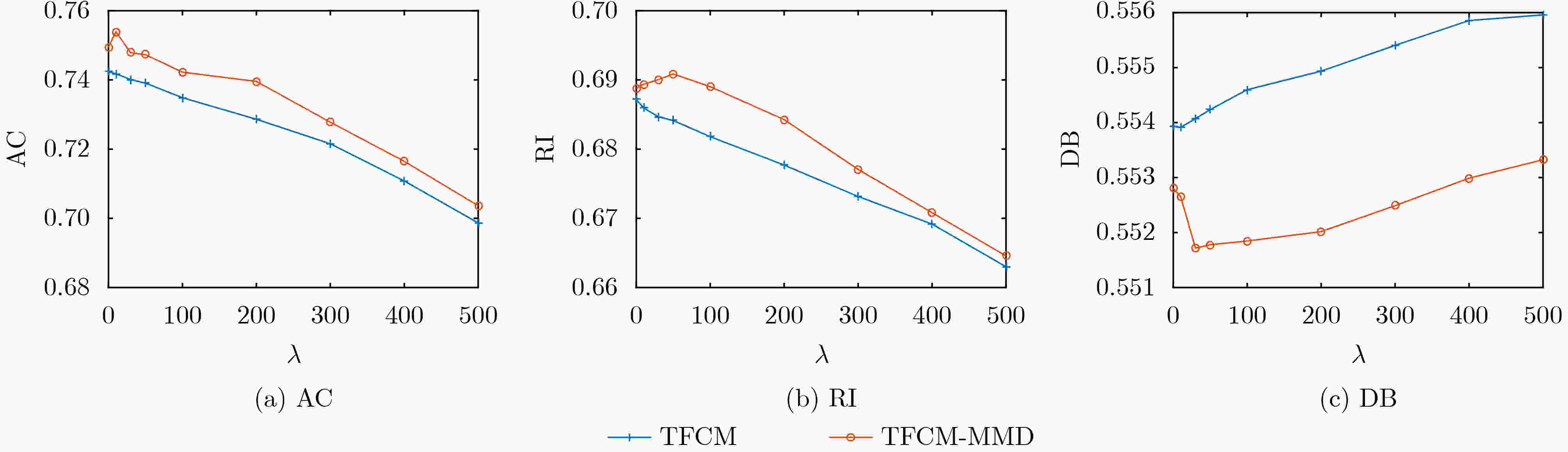
S1_1-T1_1 S1_2-T1_2 S2-T2_1 S2-T2_2 S2-T2_3 FCM-MMD 0.633 0.330 0.767 0.700 0.624 TFCM-MMD 0.767 0.767 0.747 0.744 0.739 CI* [0.6157, 0.9183] [0.6157, 0.9183] [0.7605, 0.7735] [0.7373, 0.7507] [0.7323, 0.7457] *最后一行是最佳方法的95%置信区间 表 3 FCM-MMD与TFCM-MMD聚类性能对比(RI)
S1_1-T1_1 S1_2-T1_2 S2-T2_1 S2-T2_2 S2-T2_3 FCM-MMD 0.639 0.310 0.694 0.660 0.611 TFCM-MMD 0.733 0.736 0.691 0.688 0.684 CI [0.5747, 0.8913] [0.5783, 0.8937] [0.6869, 0.7011] [0.6809, 0.6951] [0.6769, 0.6911] 表 4 FCM-MMD与TFCM-MMD聚类性能对比(DB)
S1_1-T1_1 S1_2-T1_2 S2-T2_1 S2-T2_2 S2-T2_3 FCM-MMD 0.923 \ 0.473 0.530 0.558 TFCM-MMD 0.797 0.797 0.552 0.550 0.556 CI [0.6531, 0.9409] [0.6531, 0.9409] [0.4654, 0.4806] [0.5224, 0.5376] [0.5484, 0.5636] -
[1] BORLEA I D, PRECUP R E, BORLEA A B, et al. A unified form of fuzzy c-means and k-means algorithms and its partitional implementation[J]. Knowledge-Based Systems, 2021, 214: 106731. doi: 10.1016/j.knosys.2020.106731 [2] 车杭骏, 陈科屹, 王雅娣, 等. 带有深度邻域信息的模糊C均值聚类算法[J]. 华中科技大学学报:自然科学版, 2022, 50(11): 135–141. doi: 10.13245/j.hust.221117CHE Hangjun, CHEN Keyi, WANG Yadi, et al. Fuzzy c-means clustering algorithm with deep neighborhood information[J]. Journal of Huazhong University of Science and Technology:Nature Science Edition, 2022, 50(11): 135–141. doi: 10.13245/j.hust.221117 [3] 白璐, 赵鑫, 孔钰婷, 等. 谱聚类算法研究综述[J]. 计算机工程与应用, 2021, 57(14): 15–26. doi: 10.3778/j.issn.1002-8331.2103-0547BAI Lu, ZHAO Xin, KONG Yuting, et al. Survey of spectral clustering algorithms[J]. Computer Engineering and Applications, 2021, 57(14): 15–26. doi: 10.3778/j.issn.1002-8331.2103-0547 [4] SHARMA K K and SEAL A. Multi-view spectral clustering for uncertain objects[J]. Information Sciences, 2021, 547: 723–745. doi: 10.1016/j.ins.2020.08.080 [5] 丁健宇, 祁云嵩, 赵呈祥. 类中心极大的多视角极大熵聚类算法[J]. 计算机应用研究, 2022, 39(4): 1019–1023,1059. doi: 10.19734/j.issn.1001-3695.2021.09.0399DING Jianyu, QI Yunsong, and ZHAO Chengxiang. Multi-view maximum entropy clustering algorithm with center distance maximization[J]. Application Research of Computers, 2022, 39(4): 1019–1023,1059. doi: 10.19734/j.issn.1001-3695.2021.09.0399 [6] 李烨桐, 郭洁, 祁霖, 等. 密度敏感模糊核最大熵聚类算法[J]. 控制理论与应用, 2022, 39(1): 67–82. doi: 10.7641/CTA.2021.10168LI Yetong, GUO Jie, QI Lin, et al. Density-sensitive fuzzy kernel maximum entropy clustering algorithm[J]. Control Theory &Applications, 2022, 39(1): 67–82. doi: 10.7641/CTA.2021.10168 [7] 卢娜, 张广涛, 刘付鑫, 等. 基于LTSA与谱聚类的水电机组振动故障诊断方法[J]. 武汉大学学报:工学版, 2021, 54(11): 1064–1069. doi: 10.14188/j.1671-8844.2021-11-011LU Na, ZHANG Guangtao, LIU Fuxin, et al. Vibrant fault diagnosis method for hydroelectric unit based on LTSA and spectral clustering[J]. Engineering Journal of Wuhan University, 2021, 54(11): 1064–1069. doi: 10.14188/j.1671-8844.2021-11-011 [8] 徐金东, 赵甜雨, 冯国政, 等. 基于上下文模糊C均值聚类的图像分割算法[J]. 电子与信息学报, 2021, 43(7): 2079–2086. doi: 10.11999/JEIT200263XU Jindong, ZHAO Tianyu, FENG Guozheng, et al. Image segmentation algorithm based on context fuzzy c-means clustering[J]. Journal of Electronics &Information Technology, 2021, 43(7): 2079–2086. doi: 10.11999/JEIT200263 [9] WANG Feng, JIAO Lianmeng, and PAN Quan. A survey on unsupervised transfer clustering[C]. 2021 Chinese Control Conference, Shanghai, China, 2021: 7361–7365. [10] KONG Shu and WANG Donghui. Transfer heterogeneous unlabeled data for unsupervised clustering[C]. The 21st International Conference on Pattern Recognition, Tsukuba, Japan, 2012: 1193–1196. [11] DENG Zhaohong, JIANG Yizhang, CHUNG F L, et al. Transfer prototype-based fuzzy clustering[J]. IEEE Transactions on Fuzzy Systems, 2016, 24(5): 1210–1232. doi: 10.1109/TFUZZ.2015.2505330 [12] GARGEES R, KELLER J M, and POPESCU M. TLPCM: Transfer learning possibilistic C-means[J]. IEEE Transactions on Fuzzy Systems, 2021, 29(4): 940–952. doi: 10.1109/tfuzz.2020.3005273 [13] JIAO Lianmeng, WANG Feng, LIU Zhunga, et al. TECM: Transfer learning-based evidential c-means clustering[J]. Knowledge-Based Systems, 2022, 257: 109937. doi: 10.1016/j.knosys.2022.109937 [14] WANG Rongrong, ZHOU Jin, LIU Xiangdao, et al. Transfer clustering based on Gaussian mixture model[C]. 2019 IEEE Symposium Series on Computational Intelligence, Xiamen, China, 2019: 2522–2526. [15] DANG Bozhan, ZHOU Jin, LIU Xiangdao, et al. Transfer learning based kernel fuzzy clustering[C]. 2019 International Conference on Fuzzy Theory and Its Applications, New Taipei, China, 2019: 21–25. [16] 秦军, 张远鹏, 蒋亦樟, 等. 多代表点自约束的模糊迁移聚类[J]. 山东大学学报:工学版, 2019, 49(2): 107–115. doi: 10.6040/j.issn.1672-3961.0.2018.458QIN Jun, ZHANG Yuanpeng, JIANG Yizhang, et al. Transfer fuzzy clustering based on self-constraint of multiple medoids[J]. Journal of Shandong University:Engineering Science, 2019, 49(2): 107–115. doi: 10.6040/j.issn.1672-3961.0.2018.458 [17] 王丽娟, 丁世飞, 丁玲. 基于迁移学习的软子空间聚类算法[J]. 南京大学学报:自然科学, 2020, 56(4): 515–523. doi: 10.13232/j.cnki.jnju.2020.04.009WANG Lijuan, DING Shifei, and DING Ling. Soft subspace clustering algorithm based on transfer learning[J]. Journal of Nanjing University:Natural Science, 2020, 56(4): 515–523. doi: 10.13232/j.cnki.jnju.2020.04.009 [18] 陈爱国, 王士同. 具有隐私保护功能的知识迁移聚类算法[J]. 电子与信息学报, 2016, 38(3): 523–531. doi: 10.11999/JEIT150645CHEN Aiguo and WANG Shitong. Knowledge transfer clustering algorithm with privacy protection[J]. Journal of Electronics &Information Technology, 2016, 38(3): 523–531. doi: 10.11999/JEIT150645 [19] 聂飞, 高艳丽, 邓赵红, 等. 可能性匹配知识迁移原型聚类算法[J]. 智能系统学报, 2020, 15(5): 978–989. doi: 10.11992/tis.201810028NIE Fei, GAO Yanli, DENG Zhaohong, et al. Possibility-matching based knowledge transfer prototype clustering algorithm[J]. CAAI Transactions on Intelligent Systems, 2020, 15(5): 978–989. doi: 10.11992/tis.201810028 [20] 夏洋洋, 刘渊, 黄亚东. 中心约束的跨源学习可能性C均值聚类算法[J]. 计算机工程与应用, 2018, 54(5): 72–78. doi: 10.3778/j.issn.1002-8331.1610-0055XIA Yangyang, LIU Yuan, and HUANG Yadong. Central-constraints possibilistic C-means algorithms based on source domain[J]. Computer Engineering and Applications, 2018, 54(5): 72–78. doi: 10.3778/j.issn.1002-8331.1610-0055 [21] DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Self-taught clustering[C]. The 25th International Conference on Machine Learning, Helsinki, Finland, 2008: 200–207. [22] YANG Liu, JING Liping, LIU Bo, et al. Common latent space identification for heterogeneous co-transfer clustering[J]. Neurocomputing, 2017, 269: 29–39. doi: 10.1016/j.neucom.2016.08.148 [23] JIANG Yizhang, GU Xiaoqing, WU Dongrui, et al. A novel negative-transfer-resistant fuzzy clustering model with a shared cross-domain transfer latent space and its application to brain CT image segmentation[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2021, 18(1): 40–52. doi: 10.1109/TCBB.2019.2963873 [24] XIA Kaijian, YIN Hongsheng, JIN Yong, et al. Cross-domain brain CT image smart segmentation via shared hidden space transfer FCM clustering[J]. ACM Transactions on Multimedia Computing, Communications, and Applications, 2020, 16(2s): 61. doi: 10.1145/3357233 [25] 齐晓轩, 都丽, 洪振麒. 基于流形距离核的自适应迁移谱聚类算法[J]. 计算机应用与软件, 2020, 37(8): 265–273. doi: 10.3969/j.issn.1000-386x.2020.08.046Qi Xiaoxuan, DU Li, and HONG Zhenqi. An adaptive transfer spectral clustering algorithm based on manifold distance kernel[J]. Computer Applications and Software, 2020, 37(8): 265–273. doi: 10.3969/j.issn.1000-386x.2020.08.046 [26] 张晓彤, 张宪超, 刘晗. 基于特征和实例迁移的加权多任务聚类[J]. 计算机学报, 2019, 42(12): 2614–2630. doi: 10.11897/SP.J.1016.2019.02614ZHANG Xiaotong, ZHANG Xianchao, and LIU Han. Weighed multi-task clustering by feature and instance transfer[J]. Chinese Journal of Computers, 2019, 42(12): 2614–2630. doi: 10.11897/SP.J.1016.2019.02614 [27] 王丽娟, 张霖, 尹明, 等. 基于正交基的多视图迁移谱聚类[J]. 计算机工程, 2022, 48(10): 37–44,54. doi: 10.19678/j.issn.1000-3428.0063091WANG Lijuan, ZHANG Lin, YIN Ming, et al. Orthogonal basis-based multiview transfer spectral clustering[J]. Computer Engineering, 2022, 48(10): 37–44,54. doi: 10.19678/j.issn.1000-3428.0063091 [28] YU Litao, DANG Yanzhong, and YANG Guangfei. Transfer clustering via constraints generated from topics[C]. 2012 IEEE International Conference on Systems, Man, and Cybernetics, Seoul, Korea (South), 2012: 3203–3208. [29] LIU Yang, JING Liping, and YU Jian. Heterogeneous co-transfer spectral clustering[C]. The 9th International Conference on Rough Sets and Knowledge Technology, Shanghai, China, 2014: 352–363. [30] LI Sheng and FU Yun. Unsupervised transfer learning via low-rank coding for image clustering[C]. 2016 International Joint Conference on Neural Networks, Vancouver, Canada, 2016: 1795–1802. [31] PAL N R and BEZDEK J C. On cluster validity for the fuzzy c-means model[J]. IEEE Transactions on Fuzzy Systems, 1995, 3(3): 370–379. doi: 10.1109/91.413225 [32] HATHAWAY R J, BEZDEK J C, and TUCKER W T. An improved convergence theory for the fuzzy c-means clustering algorithms[J]. Analysis of Fuzzy Information, 1987, 3: 123–131. [33] GAN G and WU J. A convergence theorem for the fuzzy subspace clustering (FSC) algorithm[J]. Pattern Recognition, 2008, 41(6): 1939–1947. doi: 10.1016/j.patcog.2007.11.011 [34] COCOSCO C A, KOLLOKIAN V, KWAN R K S, et al. BrainWeb: Online interface to a 3D MRI simulated brain database[J]. NeuroImage, 1997, 5(4): 425. -





 下载:
下载:

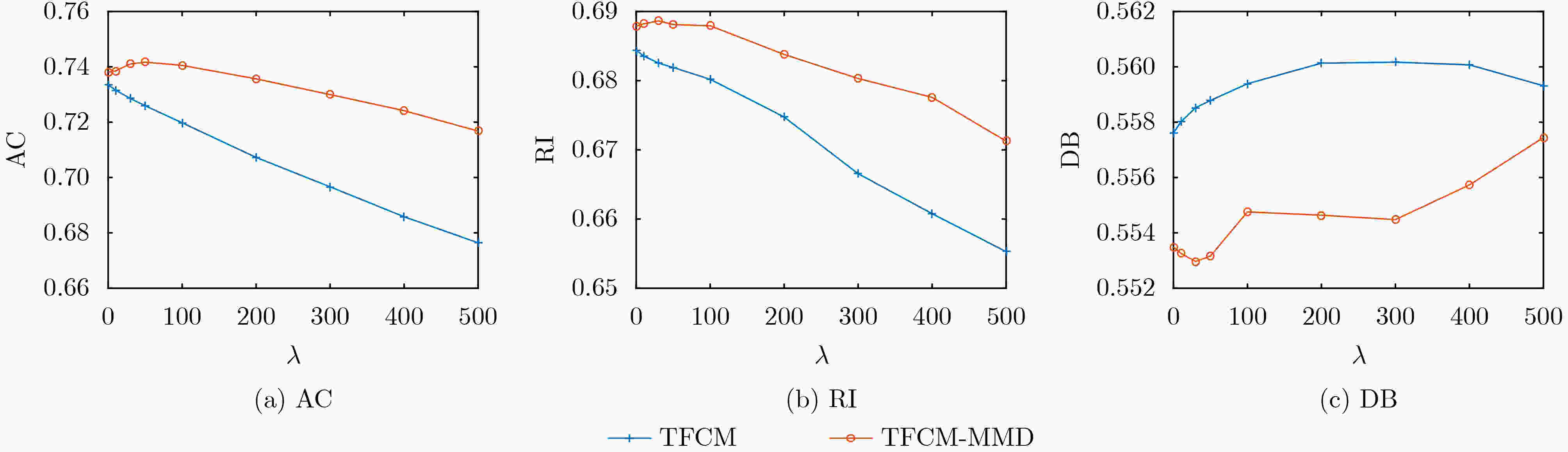
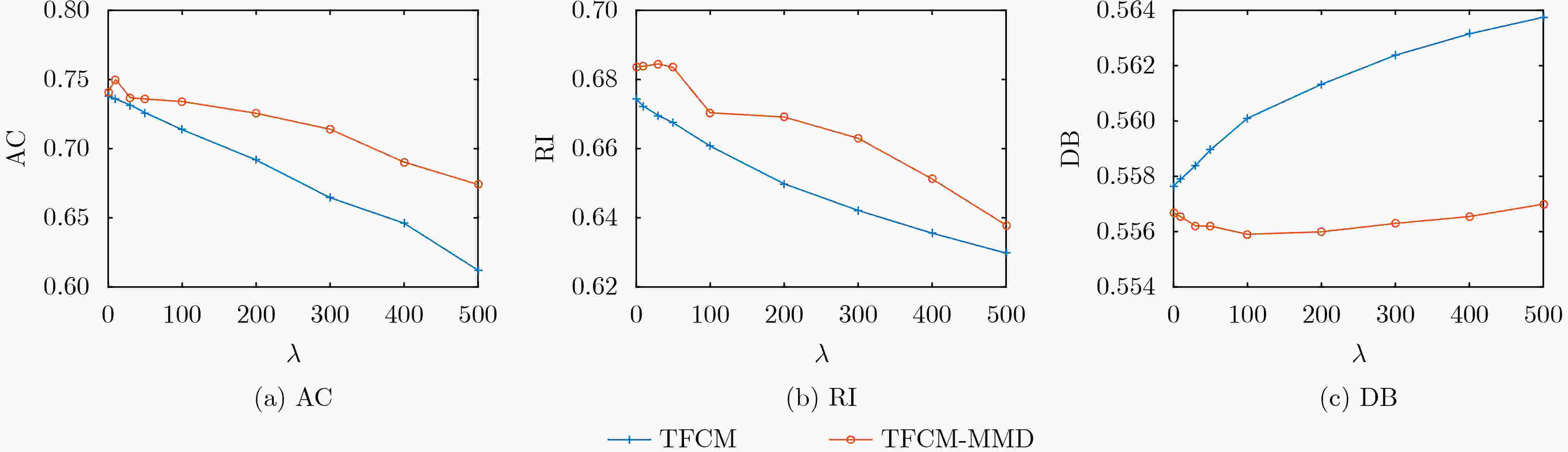
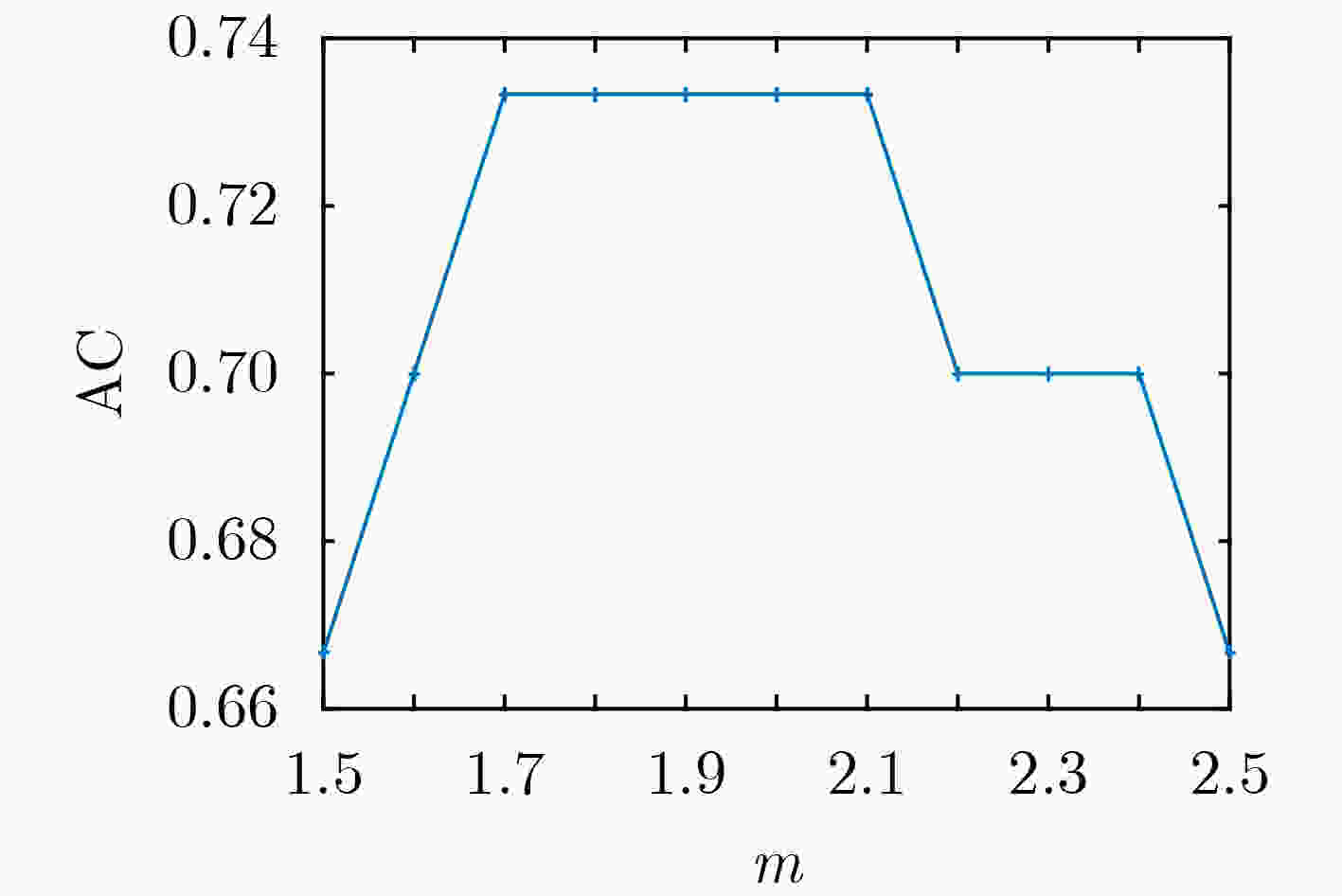
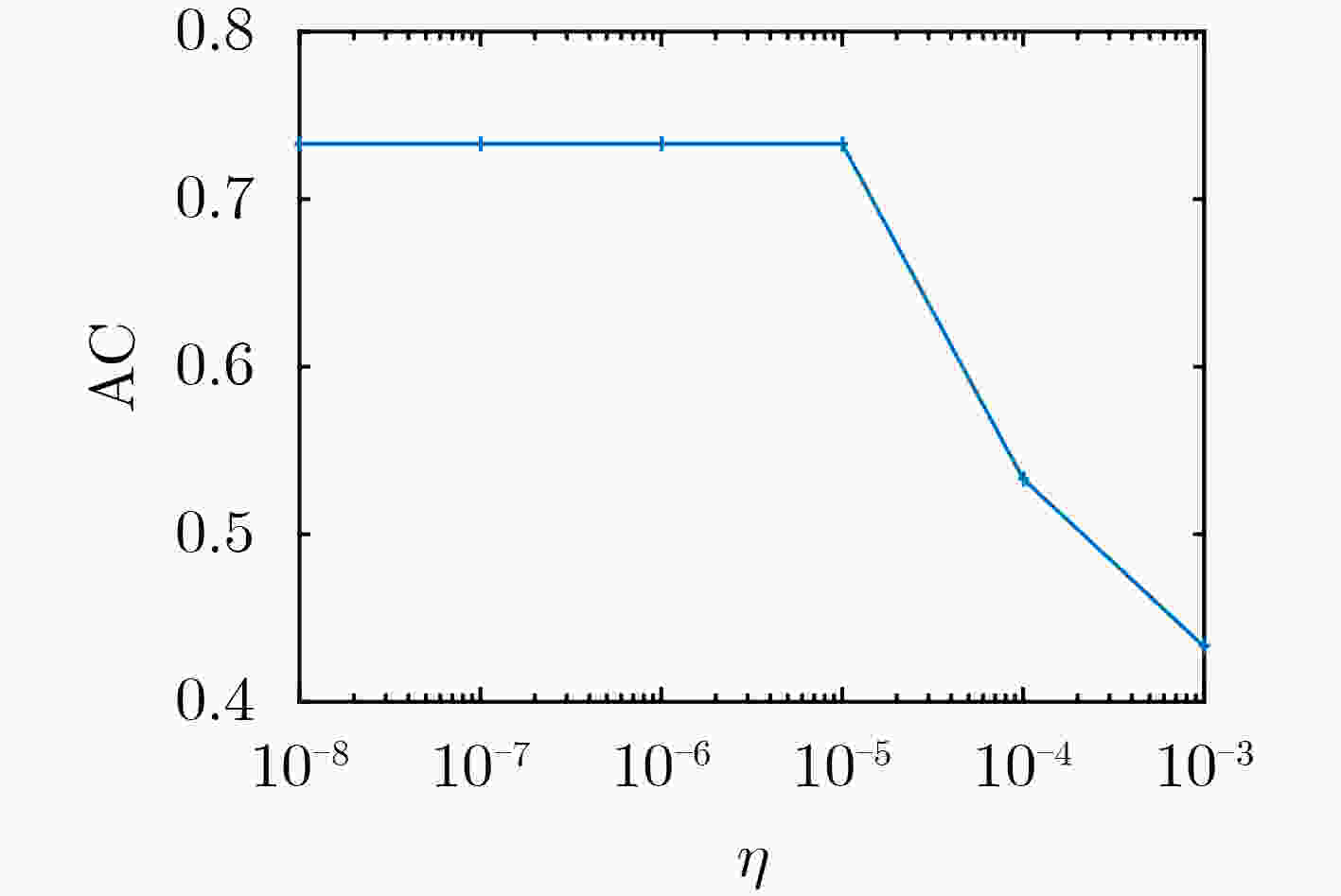



 下载:
下载:
