基于生成对抗数据增强支持向量机的小样本信号调制识别算法

谢智东; 谭信; 袁昕旺; 杨刚; 韩裕

doi:10.11999/JEIT220624

基于生成对抗数据增强支持向量机的小样本信号调制识别算法

doi: 10.11999/JEIT220624

军事科学院国防科技创新研究院北京 100071

详细信息

作者简介:
谢智东：男，副研究员，研究方向为无人集群电磁对抗、无人集群通信、卫星通信

谭信：男，硕士生，研究方向为智能信息感知处理与传输

袁昕旺：男，硕士生，研究方向为网络通信安全

杨刚：男，硕士生，研究方向为信号处理

韩裕：男，硕士生，研究方向为信号处理

通讯作者:
谭信　tanxin2017@163.com

中图分类号: TP391.4; TN911.3
计量
- 文章访问数: 711
- HTML全文浏览量: 302
- PDF下载量: 183
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-17
- 修回日期: 2022-10-07
- 网络出版日期: 2022-10-11
- 刊出日期: 2023-06-10

Small Sample Signal Modulation Recognition Algorithm Based on Support Vector Machine Enhanced by Generative Adversarial Networks Generated Data

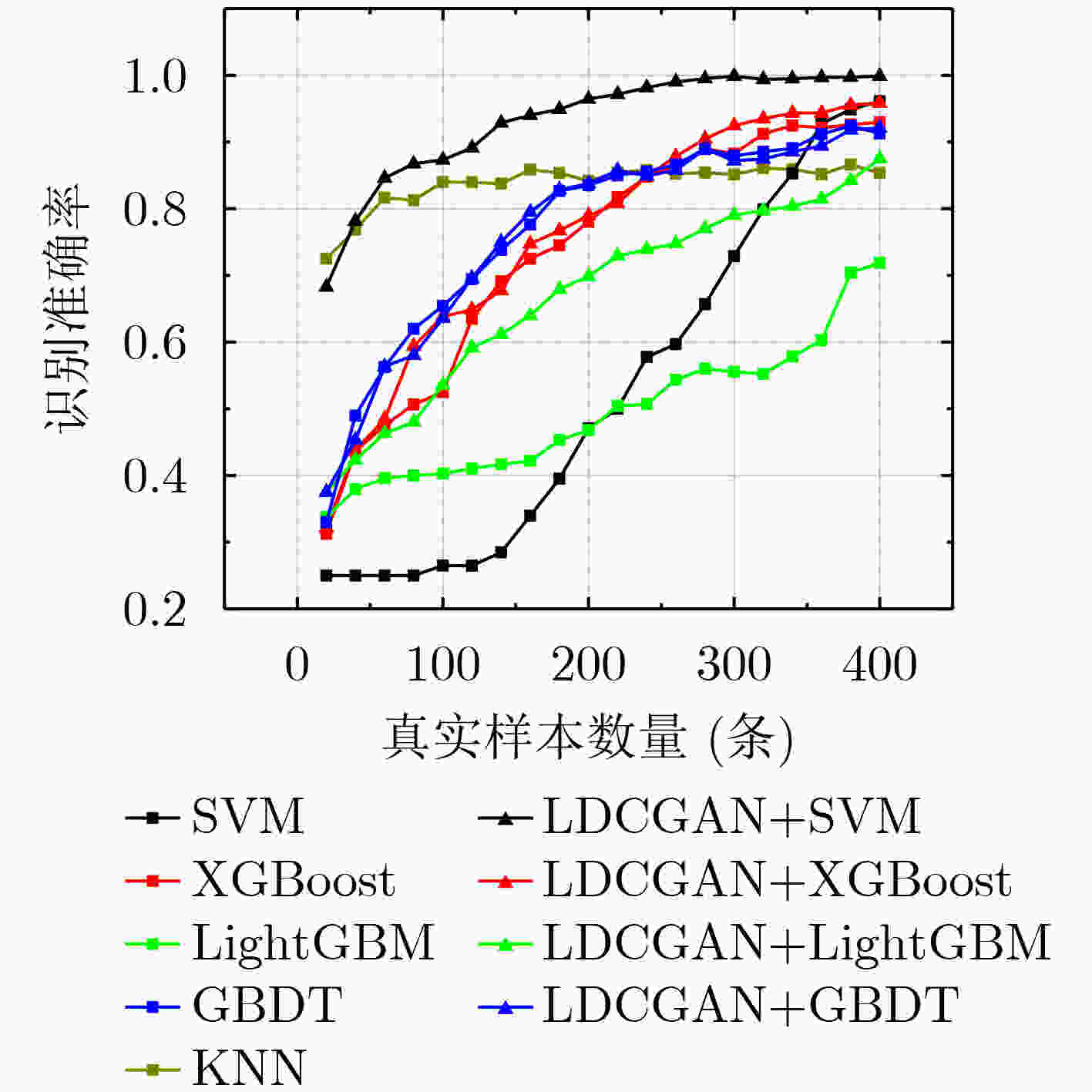
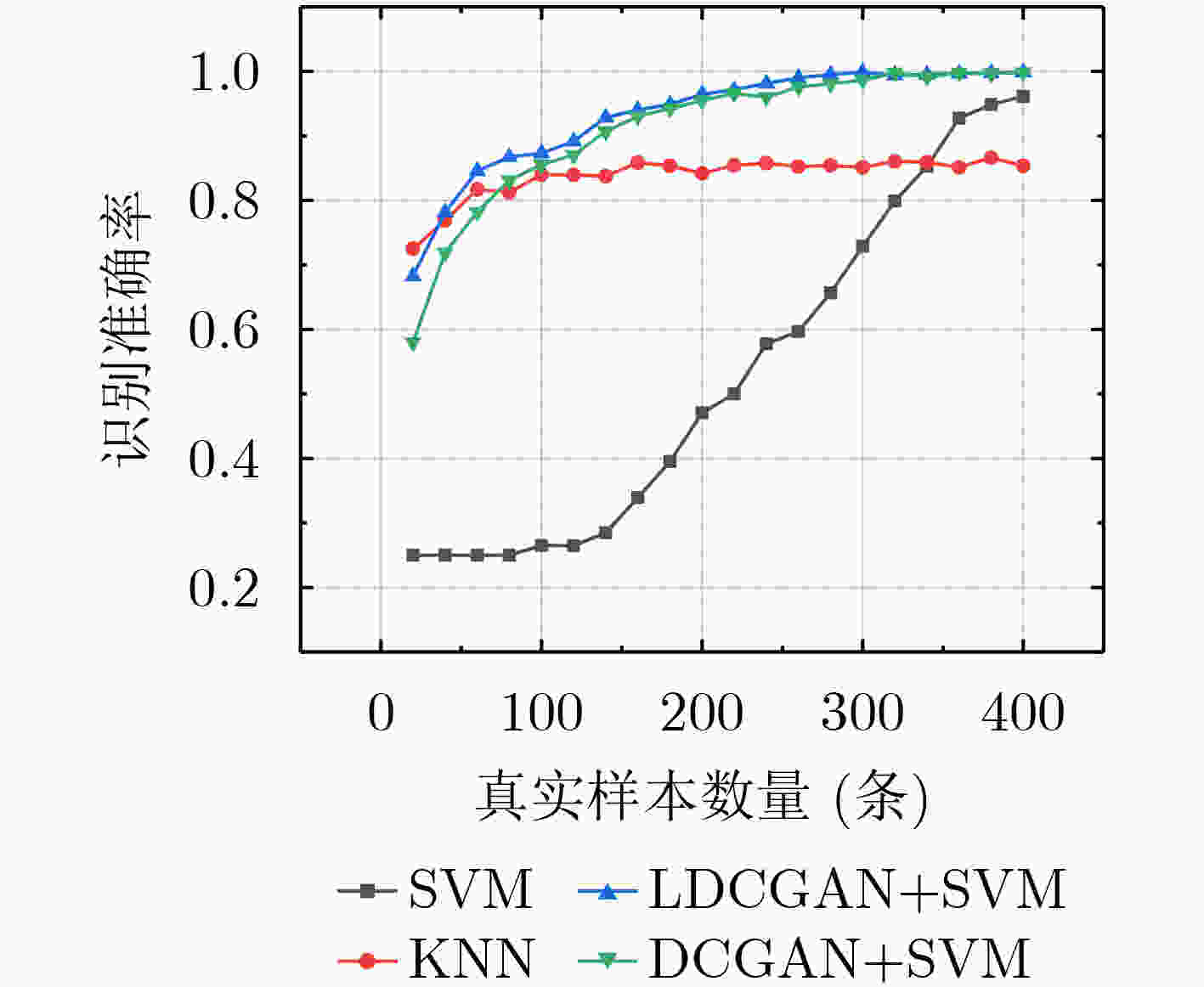
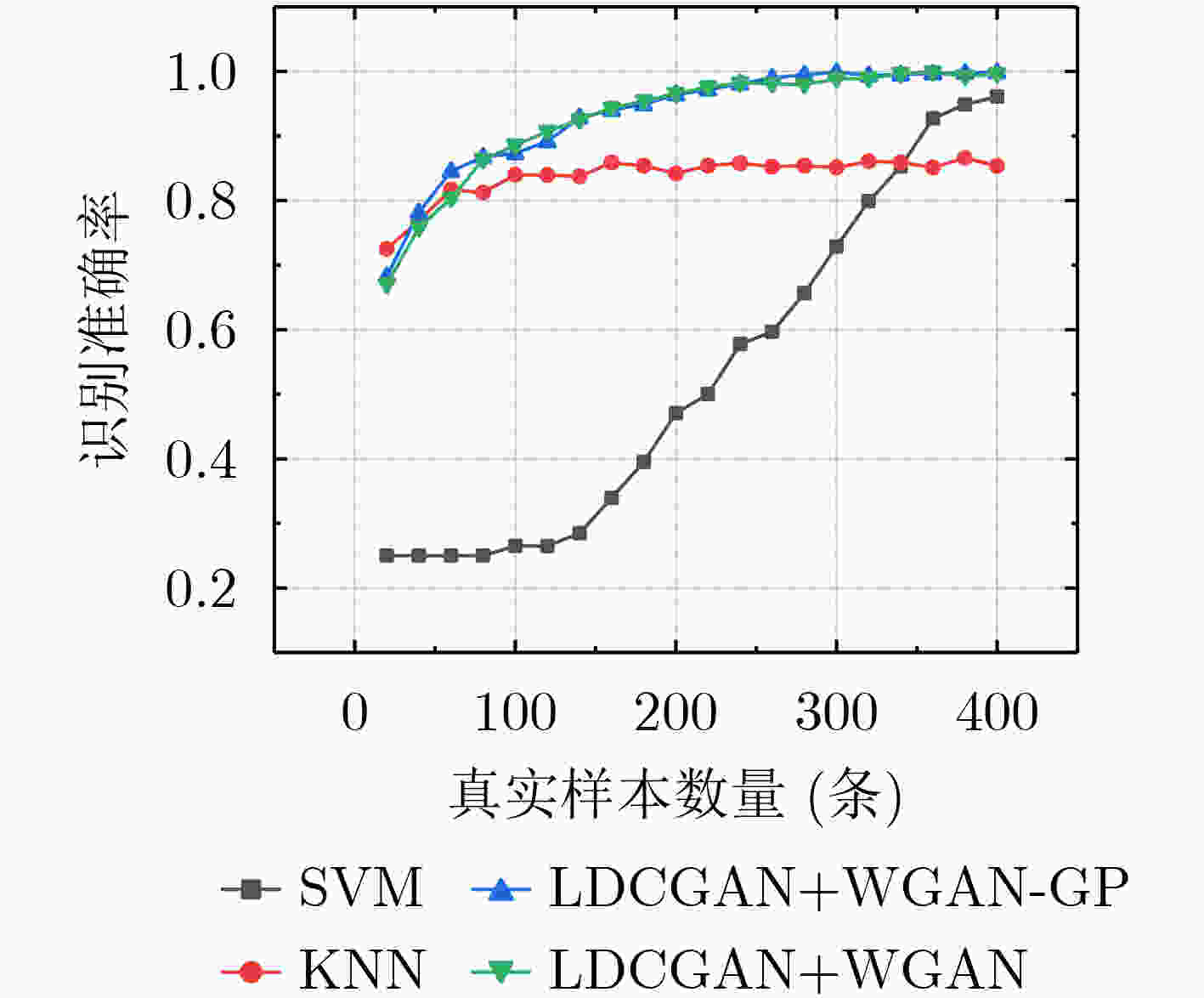
College of National Defense Technology and Innovation, Academic of Military Science, Beijing 100071, China

摘要

摘要: 着眼于解决小样本信号调制识别问题，该文首先研究了利用支持向量机(SVM)进行分类识别的理论可行性；其次根据统计学习理论，对利用生成对抗网络(GAN)生成数据增强支持向量机分类识别能力进行了理论分析；最后通过构建包含层归一化的深度卷积生成对抗网络(LDCGAN)，与普通深度卷积生成对抗网络相比，其生成数据映射至高维空间后特征更加明显，更有利于支持向量机的分类，实验验证了该生成对抗网络生成数据可以在小样本条件下实现对支持向量机分类识别能力的有效增强。
- 调制识别 /
- 生成对抗网络 /
- 支持向量机 /
- 小样本
Abstract: Focusing on solving the problem of small sample signal modulation recognition, the theoretical feasibility of using Support Vector Machine (SVM) for modulation recognition is investigated firstly; Secondly, based on statistical learning theory, a theoretical analysis of using Generative Adversarial Networks (GAN) generated data to enhance the classification ability of SVM is conducted; And finally, a Deep Convolutional Generative Adversarial Network based on Layer normalization (LDCGAN) is constructed , whose generated data has more obvious features than Deep Convolutional Generative Adversarial Networks (DCGAN) after mapping to a high-dimensional space, so the generated data is more conducive to the classification of SVM. The experiments verify that LDGAN generated data can achieve an effective enhancement of the classification ability of SVM under the condition of small samples.
- Modulation recognition /
- Generative Adversarial Networks (GAN) /
- Support Vector Machine (SVM) /
- Small samples

HTML全文

图 1 LDCGAN-SVM信号调制识别算法流程

下载: 全尺寸图片幻灯片

图 2 真实样本数量对传统机器学习算法识别效果的影响

下载: 全尺寸图片幻灯片

图 3 FM,QPSK真实样本与扩充样本时频图

下载: 全尺寸图片幻灯片

图 4 FM,QPSK真实样本与扩充样本频谱

下载: 全尺寸图片幻灯片

图 5 FM,QPSK真实样本与扩充样本同相正交信息时域图

下载: 全尺寸图片幻灯片

图 6 LDCGAN混合不同机器学习算法识别对比

下载: 全尺寸图片幻灯片

图 7 不同训练epoch次数对LDCGAN+SVM扩充识别影响

下载: 全尺寸图片幻灯片

图 8 层归一化对模型识别效果的影响

下载: 全尺寸图片幻灯片

图 9 WGAN-GP与WGAN损失函数识别效果对比

下载: 全尺寸图片幻灯片

图 10 WGAN-GP与WGAN损失函数收敛速度对比

下载: 全尺寸图片幻灯片

图 11 FM,QPCK不同损失函数频谱图

下载: 全尺寸图片幻灯片

图 12 FM,QPCK不同损失函数同相正交信息时域图

下载: 全尺寸图片幻灯片

图 13 LDCGAN+SVM在不同真实样本数量时识别准确率

下载: 全尺寸图片幻灯片

图 14 真实样本数量、扩充样本数量与信噪比对识别准确率的影响

下载: 全尺寸图片幻灯片

图 15 识别效果受信噪比影响

下载: 全尺寸图片幻灯片

表 1 LDCGAN整体网络结构

生成网络		鉴别网络
输入	输出维度	输入	输出维度
Noise = Input(shape=(100,))	[(None,100)]	Input(shape=(1024,1,1))	[(None,1024,2,1)]
Dense(256×2×128,activation='relu')	(None,65536)	Con2D(16,(2,2),padding='same',strides=2), LeakyReLU(alpha=0.2)	(None,512,1,16)
Reshape((256,2,128))	(None,256,2,128)	LayerNormalization	(None,512,1,16)
UpSampling2D((2,1))	(None,512,2,128)	Con2D(32,(2,1),padding='same',strides=(2,1)), LeakyReLU(alpha=0.2)	(None,256,1,32)
Conv2D(128,(2,1),strides=1,padding='same', activation='relu')	(None,512,2,128)	LayerNormalization	(None,256,1,32)
BatchNormalization	(None,512,2,128)	ZeroPadding2D(padding=((1,1),(1,1)))	(None,258,3,32)
UpSampling2D((2,1))	(None,1024,2,128)	Con2D(64,(2,2),padding='valid',strides=1), LeakyReLU(alpha=0.2)	(None,257,2,64)
Conv2D(64,(2,1),strides=1,padding='same', activation='relu')	(None,1024,2,64)	LayerNormalization	(None,257,2,64)
BatchNormalization	(None,1024,2,64)	Con2D(128,(2,2),padding='same',strides=2), LeakyReLU(alpha=0.2)	(None,129,1,128)
Conv2D(32,(2,1),strides=1,padding='same', activation='relu')	(None,1024,2,32)	LayerNormalization	(None,129,1,128)
BatchNormalization	(None,1024,2,32)	Con2D(256,(2,1),padding='same',strides=1), LeakyReLU(alpha=0.2)	(None,129,1,256)
Conv2D(1,(2,1),strides=1,padding='same', activation='tanh')	(None,1024,2,1)	GlobalAveragePooling2D()	(None,256)
		Dense(1)	(None,1)

下载: 导出CSV

表 2 传统机器学习算法训练耗时(s)

	SVM	KNN	MLP	Random Forest	LightGBM	GBDT	XGBoost	AdaBoost
耗时	1.8	0.1	2.5	0.3	11.0	188.0	7.0	9.0

下载: 导出CSV

表 3 LDCGAN训练耗时(h)

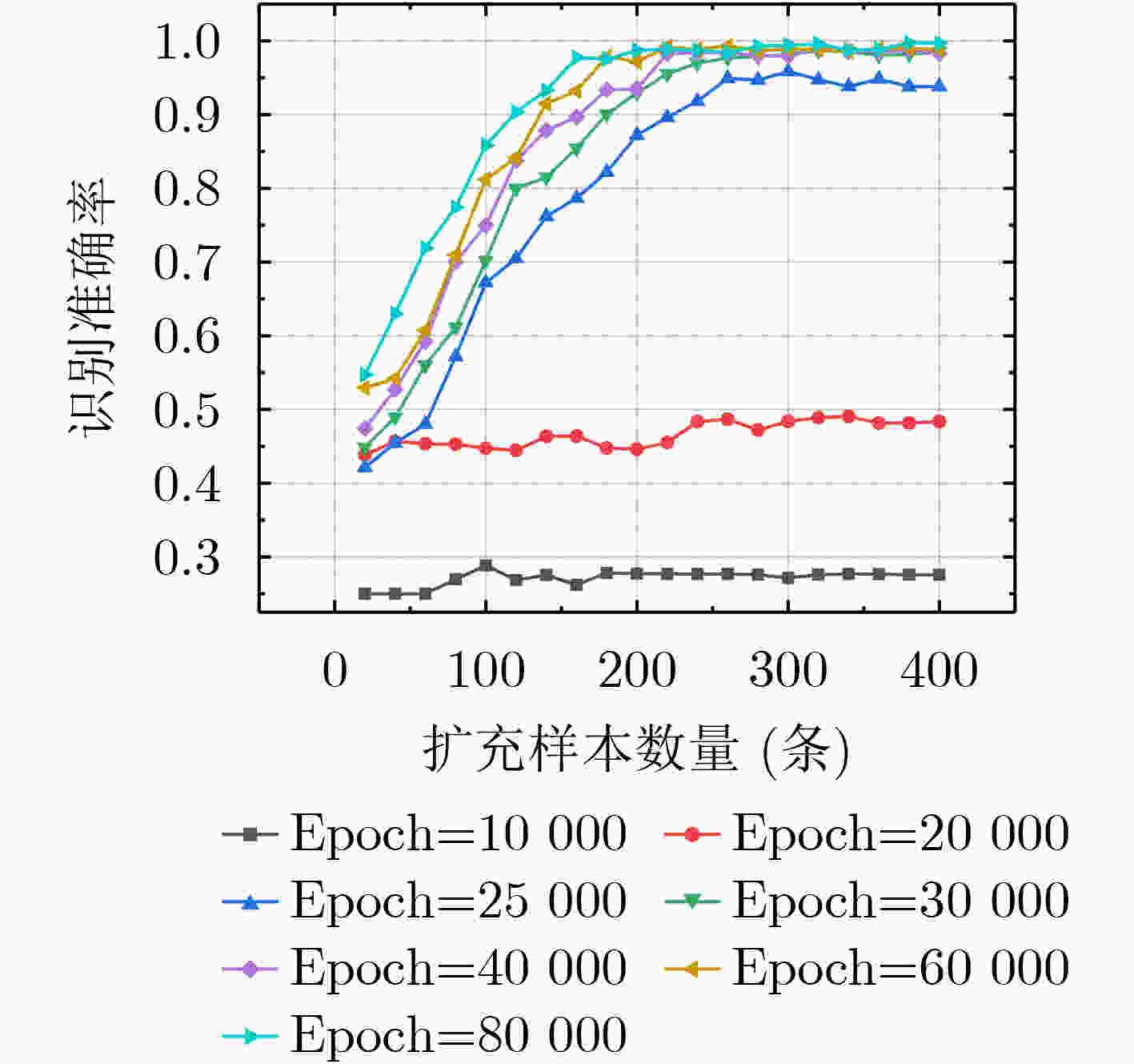
训练epoch	10000	20000	25000	30000	40000	60000	80000
耗时	0.6	1.2	1.5	1.8	2.4	3.6	4.8

下载: 导出CSV

参考文献(25)

[1]	丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2–10. doi: 10.3969/j.issn.1001-0548.2011.01.001 DING Shifei, QI Bingjuan, and TAN Hongyan. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2–10. doi: 10.3969/j.issn.1001-0548.2011.01.001
[2]	BOUTTE D and SANTHANAM B. ISI effects in a hybrid ICA-SVM modulation recognition algorithm[C]. 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2008: 457–460.
[3]	VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995.
[4]	张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32–42. doi: 10.16383/j.aas.2000.01.005 ZHANG Xuegong. Introduction to statistical learning theory and support vector machines[J]. Acta Automatica Sinica, 2000, 26(1): 32–42. doi: 10.16383/j.aas.2000.01.005
[5]	REN Mingqiu, CAI Jinyan, ZHU Yuanqing, et al. Radar emitter signal classification based on mutual information and fuzzy support vector machines[C]. 2008 9th International Conference on Signal Processing, Beijing, China, 2008: 1641–1646.
[6]	LIN Chunfu and WANG Shengde. Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 464–471. doi: 10.1109/72.991432
[7]	SUN Xiaoyong, SU Shaojing, HUANG Zhiping, et al. Blind modulation format identification using decision tree twin support vector machine in optical communication system[J]. Optics Communications, 2019, 438: 67–77. doi: 10.1016/j.optcom.2019.01.025
[8]	JAYADEVA, KHEMCHANDANI R, and CHANDRA S. Twin support vector machines for pattern classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(5): 905–910. doi: 10.1109/TPAMI.2007.1068
[9]	QIAN Chen, ZENG Zhixin, and WANG Hua. Study on the impacts of feature indexes on intelligent identification of communication modulation mode[C]. 2021 6th International Symposium on Computer and Information Processing Technology (ISCIPT), Changsha, China, 2021: 325–332.
[10]	XIONG Wei, ZHANG Lin, MCNEIL M, et al. SYMMeTRy: Exploiting MIMO self-similarity for under-determined modulation recognition[J]. IEEE Transactions on Mobile Computing, 2022, 21(11): 4111–4124. doi: 10.1109/TMC.2021.3065891
[11]	LI Shitong, QUAN Daying, WANG Xiaofeng, et al. LPI Radar signal modulation recognition with feature fusion based on time- frequency transforms[C]. 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 2021: 1–6.
[12]	LIU Gaohui and CAO Jiakun. Research on modulation recognition of OFDM signal based on hierarchical iterative support vector machine[C]. 2020 International Conference on Communications, Information System and Computer Engineering (CISCE), Kuala Lumpur, Malaysia, 2020: 38–44.
[13]	DONG Shuli, LI Zhipeng, and ZHAO Linfeng. A modulation recognition algorithm based on cyclic spectrum and SVM classification[C]. 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 2020: 2123–2127.
[14]	HOSSEINZADEH H, EINALOU Z, and RAZZAZI F. A weakly supervised representation learning for modulation recognition of short duration signals[J]. Measurement, 2021, 178: 109346. doi: 10.1016/j.measurement.2021.109346
[15]	FU Ying and WANG Xing. Radar signal recognition based on modified semi-supervised SVM algorithm[C]. 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 2017: 2336−2340.
[16]	GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672−2680.
[17]	RATLIFF L J, BURDEN S A, and SASTRY S S. Characterization and computation of local Nash equilibria in continuous games[C]. 2013 51st Annual Allerton Conference on Communication, Control, and Computing, Monticello, USA, 2013: 917–924.
[18]	王坤峰, 苟超, 段艳杰, 等. 生成式对抗网络GAN的研究进展与展望[J]. 自动化学报, 2017, 43(3): 321–332. doi: 10.16383/j.aas.2017.y000003 WANG Kunfeng, GOU Chao, DUAN Yanjie, et al. Generative adversarial networks: The state of the art and beyond[J]. Acta Automatica Sinica, 2017, 43(3): 321–332. doi: 10.16383/j.aas.2017.y000003
[19]	RADFORD A, METZ L, and CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[C]. 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016.
[20]	ARJOVSKY M, CHINTALA S, and BOTTOU L. Wasserstein GAN[J]. arXiv: 1701.07875, 2017.
[21]	SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 1–9.
[22]	KHODJA H A and BOUDJENIBA O. Application of WGAN-GP in recommendation and Questioning the relevance of GAN-based approaches[J]. arXiv: 2204.12527, 2022.
[23]	LIU Fenglin, REN Xuancheng, ZHANG Zhiyuan, et al. Rethinking skip connection with layer normalization in transformers and resNets[J]. arXiv: 2105.07205, 2021.
[24]	DeepSig. DATASET: RADIOML 2018.01A (NEW)[EB/OL]. https://www.deepsig.ai/datasets, 2021.
[25]	FRIEDMAN J H. Greedy function approximation: A gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189–1232. doi: 10.1214/aos/1013203451