Robustness Enhancement Method of Deep Learning Model Based on Information Bottleneck
-
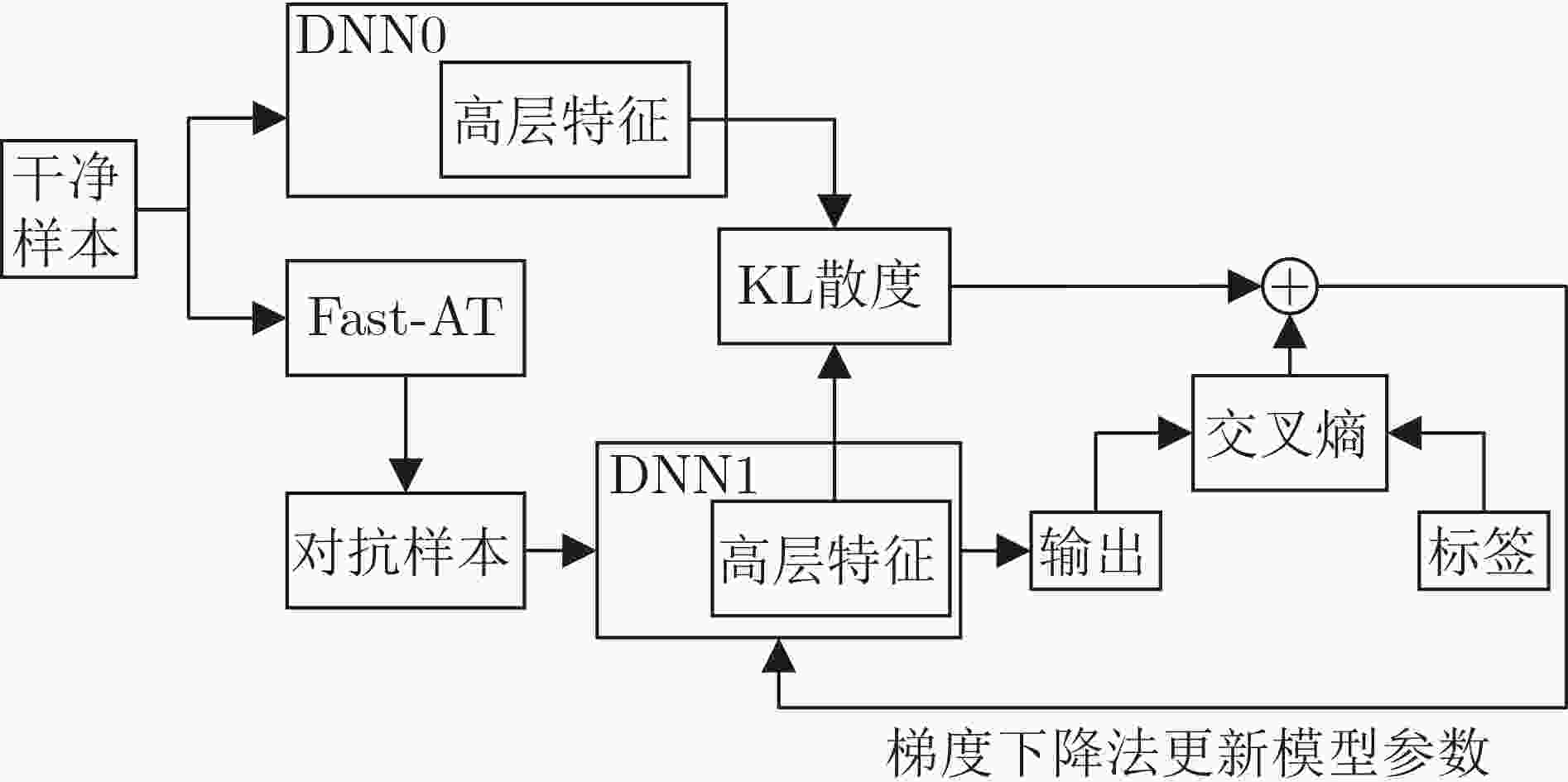
摘要: 作为深度学习技术的核心算法,深度神经网络容易对添加了微小扰动的对抗样本产生错误的判断,这种情况的出现对深度学习模型的安全性带来了新的挑战。深度学习模型对对抗样本的抵抗能力被称为鲁棒性,为了进一步提升经过对抗训练算法训练的模型的鲁棒性,该文提出一种基于信息瓶颈的深度学习模型对抗训练算法。其中,信息瓶颈以信息论为基础,描述了深度学习的过程,使深度学习模型能够更快地收敛。所提算法使用信息瓶颈理论提出的优化目标推导出的结论,将模型中输入到线性分类层的张量加入损失函数,通过样本交叉训练的方式将干净样本与对抗样本输入模型时得到的高层特征对齐,使模型在训练过程中能够更好地学习输入样本与其真实标签的关系,最终对对抗样本具有良好的鲁棒性。实验结果表明,所提算法对多种对抗攻击均具有良好的鲁棒性,并且在不同的数据集与模型中具有泛化能力。Abstract: As the core algorithm of deep learning technology, deep neural network is easy to make wrong judgment on the adversarial examples with imperceptive perturbation. This situation brings new challenges to the security of deep learning model. The resistance of deep learning model to adversarial examples is called robustness. In order to improve the robustness of the model trained by adversarial training algorithm, an adversarial training algorithm of deep learning model based on information bottleneck is proposed. Among this, information bottleneck describes the process of deep learning based on information theory, so that the deep learning model can converge faster. The proposed algorithm uses the conclusions derived from the optimization objective proposed based on the information bottleneck theory, adds the tensor input to the linear classification layer in the model to the loss function, and aligns the clean samples with the high-level features obtained when the adversarial samples are input to the model by means of sample cross-training, so that the model can better learn the relationship between the input samples and their true labels during the training process and has finally good robustness to the adversarial samples. Experimental results show that the proposed algorithm has good robustness to a variety of adversarial attacks, and has generalization ability in different data sets and models.
-
Key words:
- Deep learning /
- Adversarial training /
- Information bottleneck /
- Adversarial example /
- Robustness
-
表 1 公式变量对照表
公式变量 名称 公式变量 名称 $L$ 目标函数 $p\left( {{\cdot}} \right)$ 边缘概率分布 $ \tilde x $ 对抗样本 $q\left( {{\cdot}} \right)$ 边缘概率分布 $y$ 网络输出 $\beta $ 信息瓶颈通过率 $z$ 隐藏变量 $H\left( {{\cdot}} \right)$ 熵 $I\left( {{\cdot}} \right)$ 互信息 ${\rm{KL}}\left( { {\cdot} } \right)$ KL散度 ${L_{{\rm{IB}}} }$ 损失函数 ${\rm{CE}}\left( { {\cdot} } \right)$ 交叉熵 表 2 使用的数据集信息
数据集名称 图片大小 是否彩色 数量(104张) 类别(种) β CIFAR100 32×32 是 6 20 10–5 CIFAR10 32×32 是 6 10 10–5 MNIST 28×28 否 7 10 10–3 Fashion-MNIST 28×28 否 7 10 10–3 表 3 不同防御方法在CIFAR10数据集上的鲁棒性(%)
干净样本 FGSM PGD-20 PGD-100 C&W DeepFool 无防御 93.0 65.9 54.2 49.7 92.0 41.9 TRADES(1/λ=6) 84.9 61.0 56.6 56.4 81.2 61.3 TRADES(1/λ=1) 88.6 56.3 49.1 48.9 84.0 59.1 ADT 86.8 60.4 52.1 51.6 52.4 – Feature Scatter 90.0 78.4 70.5 68.6 62.6 – Fast_AT 78.6 72.4 72.3 72.2 78.5 71.1 本文 85.0 79.0 78.8 78.7 84.9 73.5 表 4 Resnet18与VGG16模型在CIFAR10数据集上的鲁棒性(%)
无防御 (Resnet18) 本文 (Resnet18) 无防御 (VGG16) 本文 (VGG16) 干净样本(ε=0) 93.0 85.0 92.1 81.4 FGSM(ε=2/8/16) 83.1/65.9/66.4 84.9/79.0/78.7 83.6/47.8/28.3 81.4/79.8/75.9 PGD-40(ε=2/8/16) 79.1/51.5/45.2 84.9/78.7/77.6 81.3/24.3/11.8 81.4/79.7/74.6 C&W(ε=2/8/16) 92.7/92.0/91.0 85.0/84.9/84.8 92.0/91.5/90.7 81.3/81.2/81.2 DeepFool(ε=2/8/16) 78.3/41.9/16.5 83.5/78.5/71.5 78.6/31.8/5.1 79.2/73.5/67.0 表 5 ResNet18模型在CIFAR100数据集20分类任务上的鲁棒性(%)
攻击算法 无防御 本文 干净样本(ε=0) 76.74 66.02 FGSM(ε=2/8/16) 51.71/34.73/30.64 64.28/59.18/52.78 PGD-20(ε=2/8/16) 46.10/14.34/5.25 64.26/58.96/51.91 PGD-100(ε=2/8/16) 44.12/8.73/2.56 64.26/58.94/51.62 C&W(ε=2/8/16) 49.64/16.55/3.66 64.05/58.22/50.48 DeepFool(ε=2/8/16) 76.21/74.42/72.19 66.00/65.86/57.00 表 6 CNN网络在MNIST数据集上的鲁棒性(%)
攻击算法 无防御 本文 干净样本(ε=0) 99.1 99.1 FGSM(ε=2/8/16) 98.9/96.3/88.9 99.1/98.1/94.9 PGD(ε=2/8/16) 98.8/90.8/67.0 99.1/97.8/91.4 C&W(ε=2/8/16) 99.1/99.0/99.0 99.1/99.0/99.0 DeepFool(ε=2/8/16) 98.4/93.4/64.2 98.8/97.5/93.7 表 7 CNN网络在Fashion-MNIST数据集上的鲁棒性(%)
攻击算法 无防御 本文 干净样本(ε=0) 93.47 87.41 FGSM(ε=2/8/16) 80.13/48.09/35.17 86.18/82.74/78.40 PGD-20(ε=2/8/16) 76.27/32.76/24.23 86.14/81.90/75.04 PGD-100(ε=2/8/16) 75.41/29.11/23.88 86.14/81.78/74.10 C&W(ε=2/8/16) 93.25/91.95/90.28 87.35/87.21/86.96 DeepFool(ε=2/8/16) 77.67/25.64/0.36 86.09/82.26/76.69 -
[1] SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]. The 2nd International Conference on Learning Representations (ICLR), Banff, Canada, 2014: 1–10. [2] GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. The 3rd International Conference on Learning Representations (ICLR), San Diego, USA, 2015: 1–11. [3] MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks[C]. 6th International Conference on Learning Representations (ICLR), Vancouver, Canada, 2018: 1–28. [4] MOOSAVI-DEZFOOLI S M, FAWZI A, and FROSSARD P. DeepFool: A simple and accurate method to fool deep neural networks[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 2574–2582. [5] CARLINI N and WAGNER D. Towards evaluating the robustness of neural networks[C]. IEEE Symposium on Security and Privacy (SP), San Jose, USA, 2017: 39–57. [6] WONG E, RICE L, and KOLTER J Z. Fast is better than free: Revisiting adversarial training[C]. The 8th International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 2020: 1–17. [7] ZHENG Haizhong, ZHANG Ziqi, GU Juncheng, et al. Efficient adversarial training with transferable adversarial examples[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 1178–1187. [8] DONG Yinpeng, DENG Zhijie, PANG Tianyu, et al. Adversarial distributional training for robust deep learning[C]. The 34th International Conference on Neural Information Processing Systems (NeurIPS), Vancouver, Canada, 2020: 693. [9] WANG Hongjun, LI Guanbin, LIU Xiaobai, et al. A Hamiltonian Monte Carlo method for probabilistic adversarial attack and learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(4): 1725–1737. doi: 10.1109/TPAMI.2020.3032061 [10] CHEN Sizhe, HE Zhengbao, SUN Chengjin, et al. Universal adversarial attack on attention and the resulting dataset DAmageNet[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(4): 2188–2197. doi: 10.1109/TPAMI.2020.3033291 [11] FAN Jiameng and LI Wenchao. Adversarial training and provable robustness: A tale of two objectives[C/OL]. The 35th AAAI Conference on Artificial Intelligence, 2021: 7367–7376. [12] GOKHALE T, ANIRUDH R, KAILKHURA B, et al. Attribute-guided adversarial training for robustness to natural perturbations[C/OL]. The 35th AAAI Conference on Artificial Intelligence, 2021: 7574–7582. [13] LI Xiaoyu, ZHU Qinsheng, HUANG Yiming, et al. Research on the freezing phenomenon of quantum correlation by machine learning[J]. Computers, Materials & Continua, 2020, 65(3): 2143–2151. doi: 10.32604/cmc.2020.010865 [14] SALMAN H, SUN Mingjie, YANG G, et al. Denoised smoothing: A provable defense for pretrained classifiers[C]. The 34th International Conference on Neural Information Processing Systems (NeurIPS), Vancouver, Canada, 2020: 1841. [15] SHAO Rui, PERERA P, YUEN P C, et al. Open-set adversarial defense with clean-adversarial mutual learning[J]. International Journal of Computer Vision, 2022, 130(4): 1070–1087. doi: 10.1007/s11263-022-01581-0 [16] MUSTAFA A, KHAN S H, HAYAT M, et al. Image super-resolution as a defense against adversarial attacks[J]. IEEE Transactions on Image Processing, 2020, 29: 1711–1724. doi: 10.1109/TIP.2019.2940533 [17] GU Shuangchi, YI Ping, ZHU Ting, et al. Detecting adversarial examples in deep neural networks using normalizing filters[C]. The 11th International Conference on Agents and Artificial Intelligence (ICAART), Prague, Czech Republic, 2019: 164–173. [18] TISHBY N, PEREIRA F C, and BIALEK W. The information bottleneck method[EB/OL]. https://arxiv.org/pdf/physics/0004057.pdf, 2000. [19] TISHBY N and ZASLAVSKY N. Deep learning and the information bottleneck principle[C]. IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 2015: 1–5. [20] SHWARTZ-ZIV R and TISHBY N. Opening the black box of deep neural networks via information[EB/OL]. https://arXiv.org/abs/1703.00810, 2017. [21] KOLCHINSKY A, TRACEY B D, and WOLPERT D H. Nonlinear information bottleneck[J]. Entropy, 2019, 21(12): 1181. doi: 10.3390/e21121181 [22] ALEMI A A, FISCHER I, DILLON J V, et al. Deep variational information bottleneck[C]. The 5th International Conference on Learning Representations (ICLR), Toulon, France, 2017: 1–19. [23] SHAMIR O, SABATO S, and TISHBY N. Learning and generalization with the information bottleneck[J]. Theoretical Computer Science, 2010, 411(29/30): 2696–2711. doi: 10.1016/j.tcs.2010.04.006 [24] STILL S and BIALEK W. How many clusters? An information-theoretic perspective[J]. Neural Computation, 2004, 16(12): 2483–2506. doi: 10.1162/0899766042321751 [25] KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations (ICLR), San Diego, USA, 2015: 1–15. [26] ZHANG Hongyang, YU Yaodong, JIAO Jiantao, et al. Theoretically principled trade-off between robustness and accuracy[C]. The 36th International Conference on Machine Learning (ICML), Long Beach, USA, 2019: 7472–7482. [27] ZHANG Haichao and WANG Jianyu. Defense against adversarial attacks using feature scattering-based adversarial training[C]. The 33rd International Conference on Neural Information Processing Systems (NeurIPS), Vancouver, Canada, 2019: 164. [28] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. [29] LIU Shuying and DENG Weihong. Very deep convolutional neural network based image classification using small training sample size[C]. The 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 2015: 730–734. -






 下载:
下载:


 下载:
下载:
