Design of Luneburg Lens Antenna Based on Novel Foam Materials
-
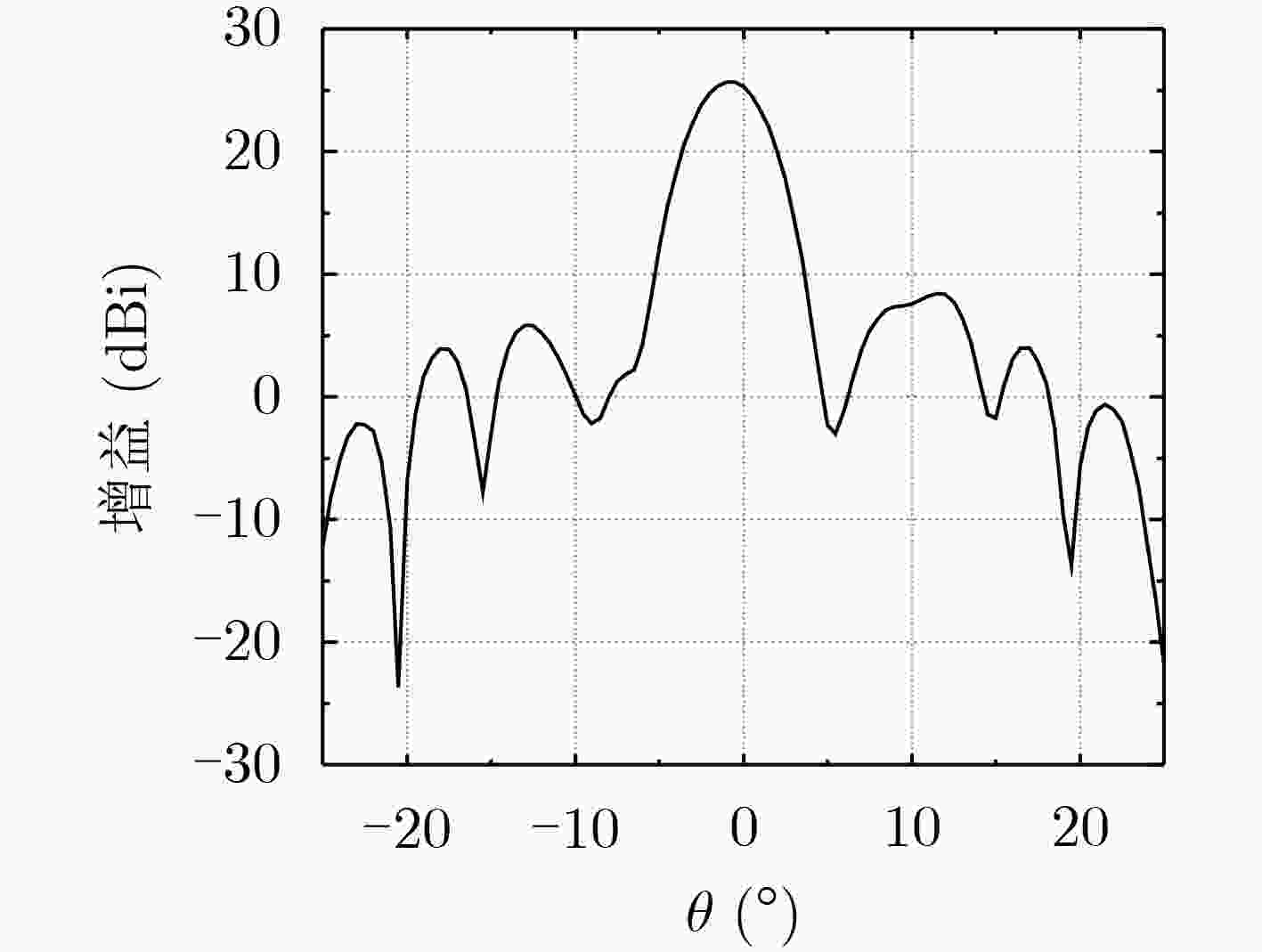
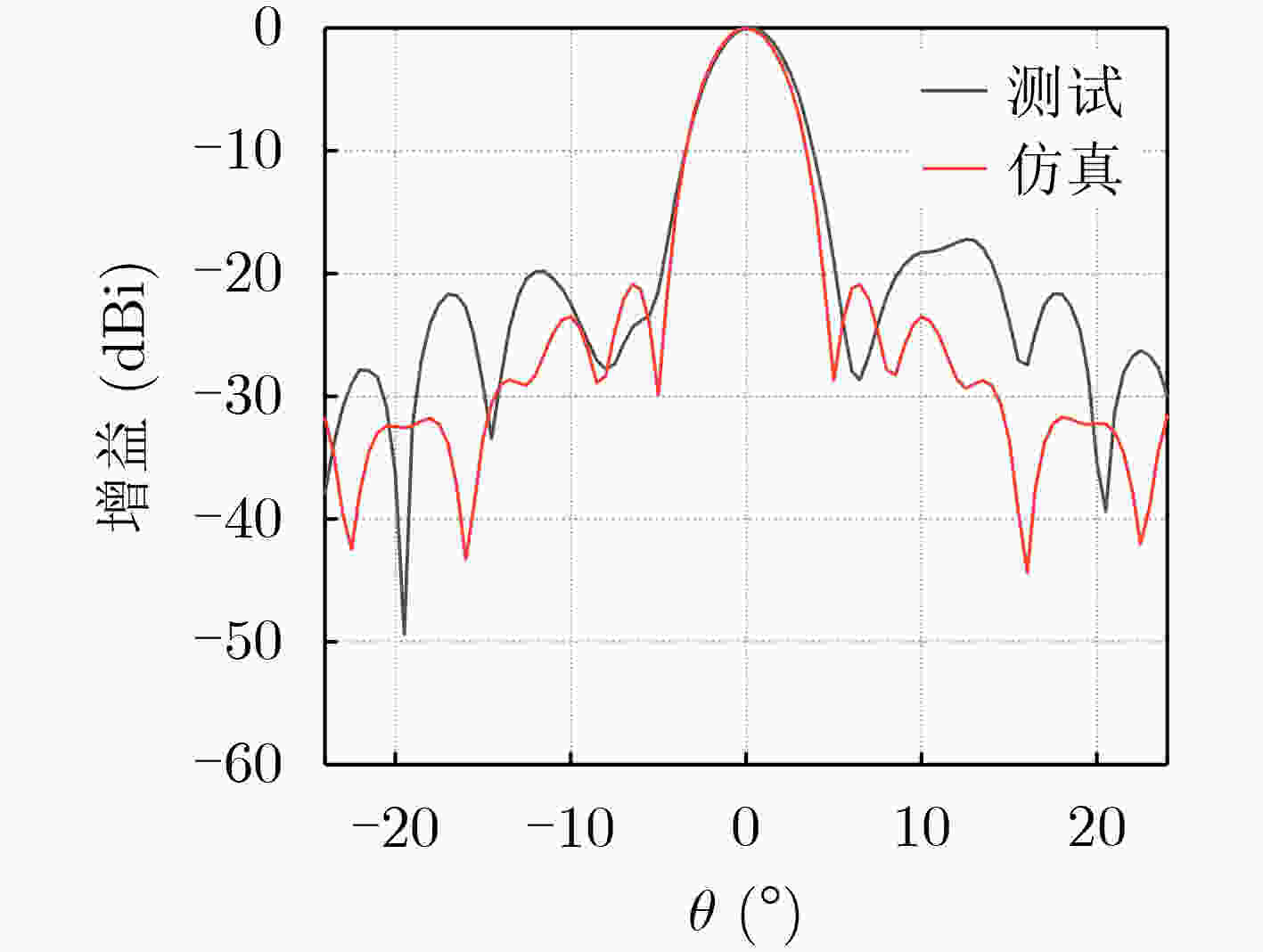
摘要: 该文利用新型泡沫材料聚甲基丙烯酰亚胺(PMI),设计了一种适用于复杂太空环境探测的毫米波龙伯透镜天线,通过将泡沫材料的密度与介电常数相关联,结合传统龙伯透镜天线的工作原理进行仿真优化,实现了小型化高增益多波束的功能。仿真结果表明:该天线工作于33.7 GHz,增益可以达到25.65 dBi,波束宽度4.17°。该设计方法为将来小型化高增益的龙伯透镜的实现提供了新的思路。Abstract: In this paper, a new type of foam material PolyMethacrylimIde (PMI) is used to design a millimeter-wave Luneburg lens antenna for the detection of complex space environment. By correlating the density of the foam material with the dielectric constant, combined with the working principle of the traditional Luneburg lens antenna, the simulation optimization is carried out, and the function of miniaturized high-gain multi-beam is realized. The simulation results show that the antenna works at 33.7 GHz, the gain can reach 25.65 dBi, and the beam width is 4.17°. This design method provides a new idea for the realization of miniaturized high-gain Luneburg lenses in the future.
-
Key words:
- Antenna /
- PMI foam /
- Luneburg lens antenna /
- High-gain antenna
-
表 1 PMI泡沫密度与其电性能参数
序号 1 2 3 4 5 6 7 8 9 密度(kg/m3) 49.75 75.72 123.64 170.69 256.88 413.76 468.34 544.68 634.62 相对介电常数 1.065 1.100 1.170 1.230 1.340 1.560 1.640 1.750 1.880 损耗正切 0.0011 0.0016 0.0031 0.0036 0.0043 0.0085 0.0092 0.0099 0.0110 -
[1] 王从思, 段宝岩, 仇原鹰, 等. 一种抛物面天线形状误差的合理评价方法[J]. 上海理工大学学报, 2006, 28(1): 14–18. doi: 10.3969/j.issn.1007-6735.2006.01.004WANG Congsi, DUAN Baoyan, QIU Yuanying, et al. Improved evaluation for calculating shape errors of parabolic antennas[J]. Journal of University of Shanghai for Science and Technology, 2006, 28(1): 14–18. doi: 10.3969/j.issn.1007-6735.2006.01.004 [2] 田小永, 吴玲玲, 殷鸣, 等. 宽频大角度新型龙勃透镜设计与快速制造[J]. 机械工程学报, 2016, 52(21): 175–181. doi: 10.3901/JME.2016.21.175TIAN Xiaoyong, WU Lingling, YIN Ming, et al. Design and rapid fabrication of broadband wide-angle flattened Luneburg lens[J]. Journal of Mechanical Engineering, 2016, 52(21): 175–181. doi: 10.3901/JME.2016.21.175 [3] 刘璟. 多波束龙伯透镜天线技术研究[D]. [硕士论文], 电子科技大学, 2010.LIU Jing. Research on multi-beam Luneburg lens antenna technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2010. [4] 钟鸣海. 分层龙伯透镜天线技术研究[D]. [硕士论文], 电子科技大学, 2009.ZHONG Minghai. Research on layered Luneburg lens antenna technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2009. [5] 郑洪振, 高黎明. 多频多波束龙伯透镜天线在海域覆盖场景下的应用[J]. 移动通信, 2022, 46(3): 87–92. doi: 10.3969/j.issn.1006-1010.2022.03.015ZHENG Hongzhen and GAO Liming. Application of multi-frequency and multi-beam Luneburg lens antennas for sea area coverage scenarios[J]. Mobile Communications, 2022, 46(3): 87–92. doi: 10.3969/j.issn.1006-1010.2022.03.015 [6] LUNEBERG R K. Mathematical Theory of Optics[M]. Providence: Brown University Press, 1944. [7] PEELER G and COLEMAN H. Microwave stepped-index Luneberg lenses[J]. IRE Transactions on Antennas and Propagation, 1958, 6(2): 202–207. doi: 10.1109/TAP.1958.1144575 [8] KOROTKOV A N, SHABUNIN S N, and CHECHETKIN V A. The cylindrical Luneburg lens discretization influence on its radiation parameters[C]. 2017 International Multi-Conferance on Engineering, Computer and Information Sciences (SIBIRCON). IEEE, Novosiboirsk, Russia, 2017, 394–398. [9] BOR J, LAFOND O, MERLET H, et al. Foam based Luneburg lens antenna at 60 GHz[J]. Progress in Electromagnetics Research Letters, 2014, 44: 1–7. doi: 10.2528/PIERL13092405 [10] RHYS T A. The design of radially symmetric lenses[J]. IEEE Transactions on Antennas and Propagation, 1970, 18(4): 497–506. doi: 10.1109/TAP.1970.1139721 [11] RONDINEAU S, HIMDI M, and SORIEUX J. A sliced spherical Luneburg lens[J]. IEEE Antennas and Wireless Propagation Letters, 2003, 2: 163–166. doi: 10.1109/LAWP.2003.819045 [12] 张广成, 刘伟, 张璋, 等. 聚甲基丙烯酰亚胺(PMI)泡沫的进展[J]. 橡塑技术与装备, 2021, 47(10): 23–30. doi: 10.13520/j.cnki.rpte.2021.10.005ZHANG Guangcheng, LIU Wei, ZHANG Zhang, et al. Progress in polymethacrylimide (PMI) foam[J]. China Rubber/Plastics Technology and Equipment, 2021, 47(10): 23–30. doi: 10.13520/j.cnki.rpte.2021.10.005 [13] KAZANTSEV O A, SHIRSHIN K V, KORNIENKO P V, et al. Achievements and prospects for the synthesis of poly(meth)acrylimide foams. Stage of the thermal imidisation of polymer precursors[J]. Cellular Polymers, 2021, 40(1): 31–52. doi: 10.1177/0262489320934258 [14] LI Jianwei, WANG Aifeng, QIN Jianbin, et al. Lightweight polymethacrylimide@copper/nickel composite foams for electromagnetic shielding and monopole antennas[J]. Composites Part A:Applied Science and Manufacturing, 2021, 140: 106144. doi: 10.1016/j.compositesa.2020.106144 [15] LUNEBURG R K. Mathematical Theory of Optics[M]. Berkeley: University of California Press, 1964: 1–448. [16] SCHRANK H E. Precision spherical Luneberg lenses for microwave antennas[C]. 1967 Seventh Electrical Insulation Conference, Chicago, USA, 1967: 179–181. -





 下载:
下载:




 下载:
下载:
