Research on OTSM Iterative Detection Algorithm in High-speed Mobile Environment
-
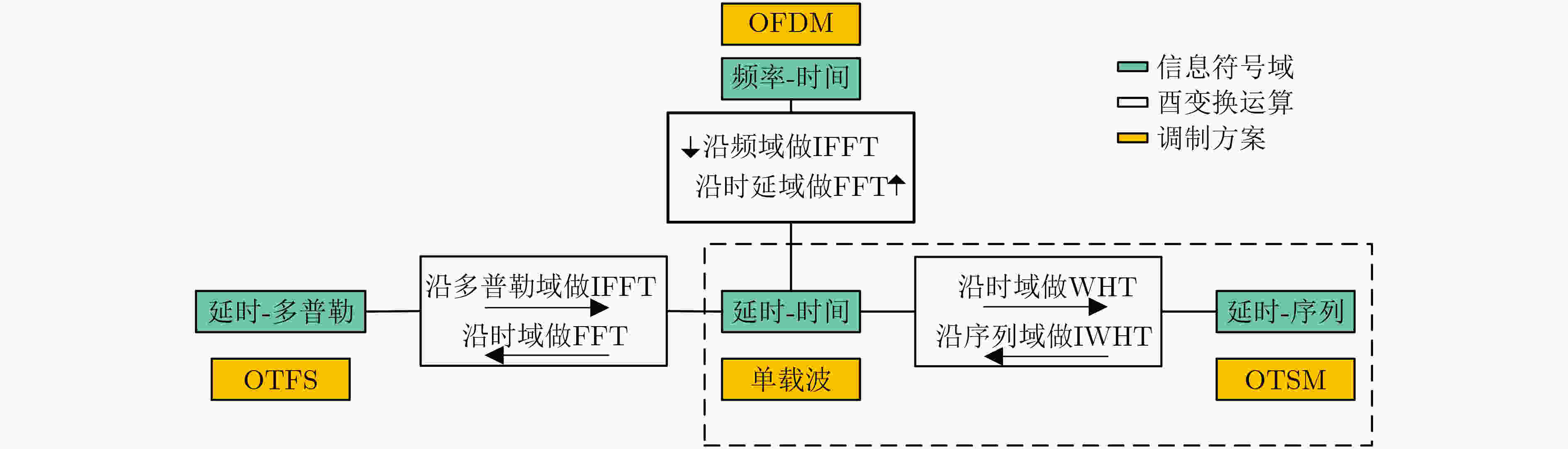
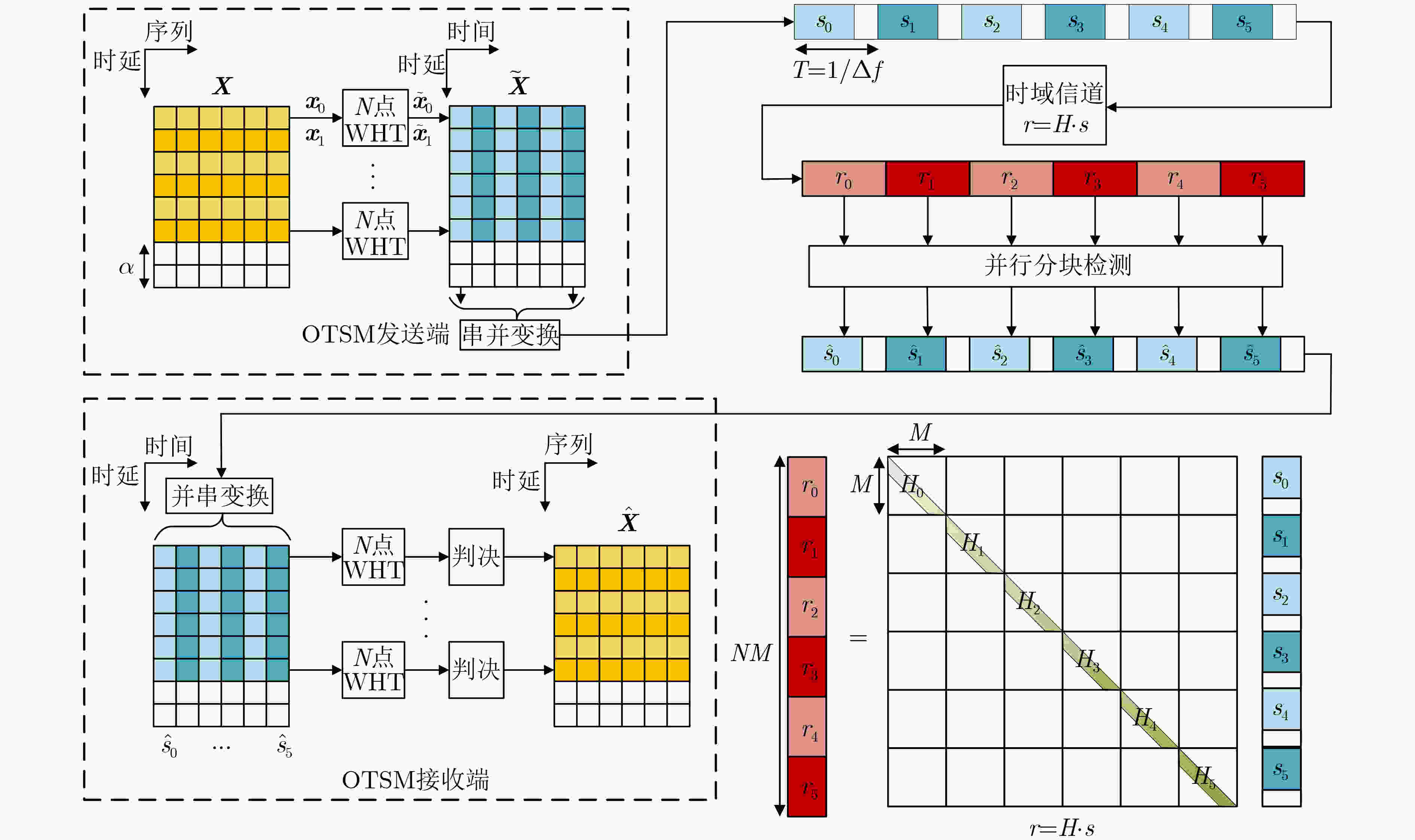
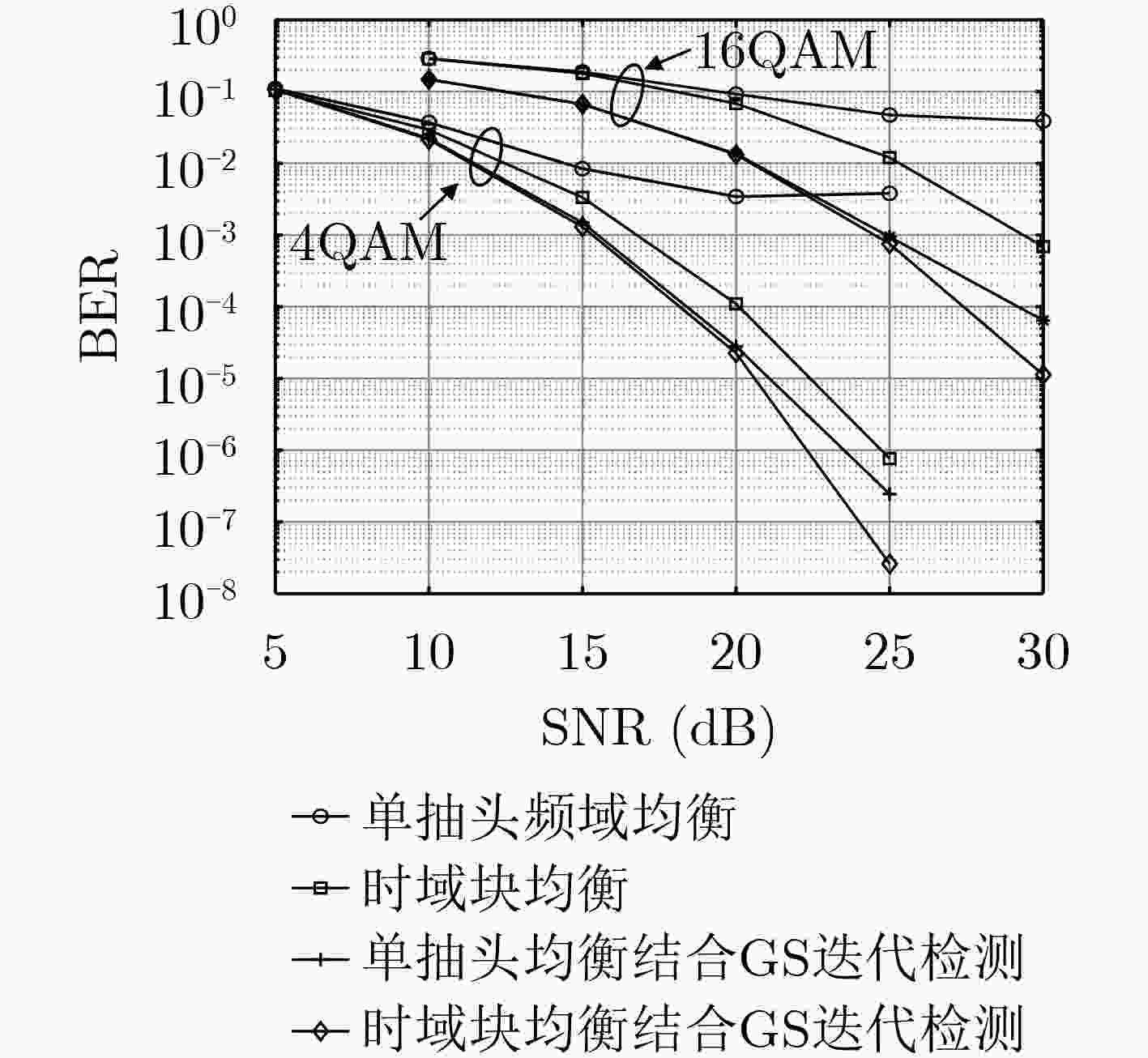
摘要: 正交时序复用( Orthogonal Time Sequency Multiplexing, OTSM)通过级联时分和沃尔什-哈达玛(WHT)复用将信息符号在时延和序列域进行复用。由于WHT在调制解调过程不需要进行复杂的乘法运算,相比于正交时频空(OTFS)调制有更低的调制复杂度。该文针对高速移动环境下的OTSM系统提出了一种二级均衡器:首先利用信道矩阵的稀疏性和带状结构在时域逐块进行低复杂度MMSE检测;随后采用高斯-赛德尔(GS)迭代检测进一步消除残余符号干扰。仿真结果表明,所提算法与基于单抽头频域均衡的GS迭代检测算法相比,采用16QAM调制且误码率为10–4时有1.8 dB性能增益。
-
关键词:
- 正交时序复用 /
- 时延-序列域 /
- 沃尔什-哈达玛变换 /
- 高斯-赛德尔迭代检测
Abstract: Orthogonal Time Sequency Multiplexing (OTSM) multiplexes information symbols in the delay-sequence domain through concatenated time division and Walsh-Hadamard multiplexing. Due to the Walsh-Hadamard Transform (WHT) does not require complex multiplication operations in the modulation and demodulation process, it has lower modulation complexity than Orthogonal Time-Frequency Space (OTFS). In this paper, a two-stage equalizer is proposed for OTSM systems in high-speed mobile environments. First, low-complexity MMSE detection is performed block-by-block in the time domain by utilizing the sparsity and band structure of the channel matrix; Then Gauss-Seid (GS) iterative detection further removes residual symbol interference. The simulation results show that, compared with the GS iterative detection algorithm based on single-tap frequency domain equalization, the proposed algorithm has a performance gain of 1.8 dB when 16QAM modulation is used and the bit error rate is 10–4. -
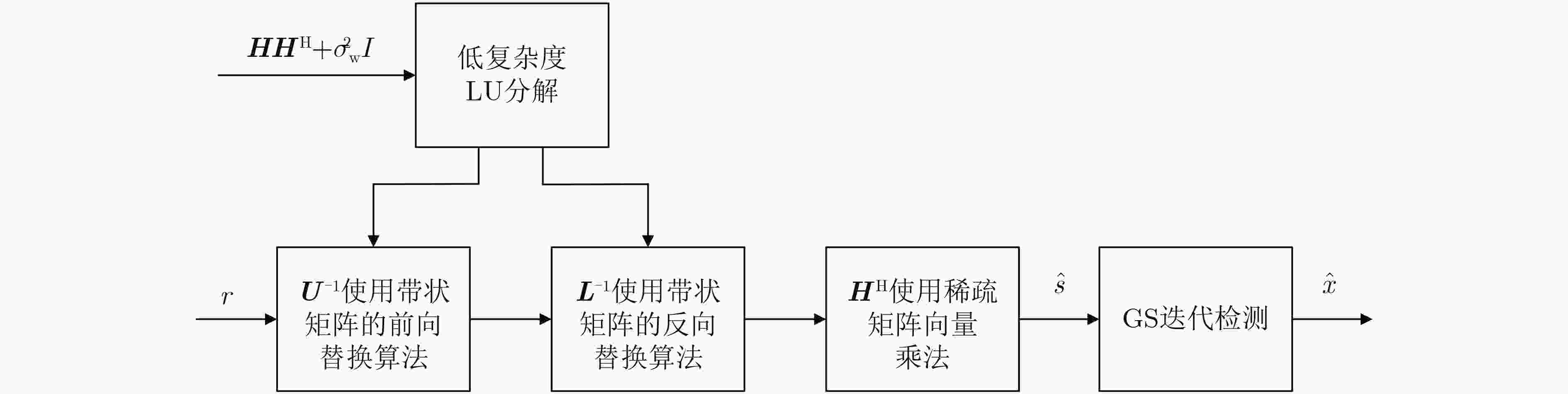
算法1 前向替换算法 计算${{\boldsymbol{r}}^{(1)} } = {{\boldsymbol{L}}^{ - 1} }{\boldsymbol{r}}$ 1:输入:下三角矩阵${{\boldsymbol{L}}_{M \times M} }$和${{\boldsymbol{r}}_{M \times 1} }$ 2:输出:${\boldsymbol{r}}_{M \times 1}^{(1)} = {\boldsymbol{L}}_{M \times M}^{ - 1}{{\boldsymbol{r}}_{M \times 1} }$ 3:${{\boldsymbol{r}}^{(1)} }(0) = {\boldsymbol{r}}(0)$ 4:for$k = 1:\alpha - 1$ do
5:${{\boldsymbol{r}}^{(1)} }(k) = {\boldsymbol{r}}(k) - \displaystyle\sum _{i = 1}^k{\boldsymbol{L}}(k,k - i){{\boldsymbol{r}}^{(1)} }(k - i)$6:end 7:for$k = \alpha :M - 1$ do
8:${{\boldsymbol{r}}^{(1)} }(k) = {\boldsymbol{r}}(k) - \displaystyle\sum _{i = 1}^{\alpha - 1}{\boldsymbol{L}}(k,k - i){{\boldsymbol{r}}^{(1)} }(k - i)$9:end 算法2 后向替换算法 计算${{\boldsymbol{r}}^{(2)} } = {{\boldsymbol{U}}^{ - 1} }{{\boldsymbol{r}}^{(1)} }$ 1:输入:上三角矩阵${{\boldsymbol{U}}_{M \times M} }$和${{\boldsymbol{r}}^{(1)} }_{M \times 1}$ 2:输出:${\boldsymbol{r}}_{M \times 1}^{(2)} = {\boldsymbol{U}}_{M \times M}^{ - 1}{\boldsymbol{r}}_{M \times 1}^{(1)}$ 3:${{\boldsymbol{r}}^{(2)} }(M - 1) = \frac{ { {{\boldsymbol{r}}^{(1)} }(M - 1)} }{ {{\boldsymbol{U}}(M - 1,M - 1)} }$ 4:for$k = M - 2:M - \alpha $do
5:${ {\boldsymbol{r} }^{(2)} }(k) = \dfrac{1}{ { {\boldsymbol{U} }(k,k)} }[{ {\boldsymbol{r} }^{(1)} }(k) - \displaystyle\sum _{i = 1}^{M - k - 1}{\boldsymbol{U} }(k,k + i){ {\boldsymbol{r} }^{(2)} }(k + i)]$6:end 7:for$k = M - \alpha - 1:0$do 8:${ {\boldsymbol{r} }^{(2)} }(k) = \dfrac{1}{ { {\boldsymbol{U} }(k,k)} }[{ {\boldsymbol{r} }^{(1)} }(k) - \displaystyle\sum _{i = 1}^{\alpha - 1}{\boldsymbol{U} }(k,k + i){ {\boldsymbol{r} }^{(2)} }(k + i)]$ 9:end 表 1 所提接收机中不同操作的计算复杂度
操作 所需复乘次数 低复杂度LU分解 $[{\alpha ^2} + 2\alpha ]MN$ 前向替换算法 $N \left[M\alpha - \dfrac{ { {\alpha ^2} } }{2} + \dfrac{\alpha }{2} - 1 \right]$ 反向替换算法 $N \left[M(\alpha - 1) - \dfrac{ { {\alpha ^2} } }{2} + \dfrac{\alpha }{2}\right]$ 稀疏矩阵向量乘法 $P(\beta + 1)MN$ 表 2 仿真参数
参数 值 调制方式 16QAM $N$ 16 $M$ 128 载波频率 4 GHz 子载波间隔 15 kHz 信道模型 EVA[20] 用户移动速度 500 km/h 信道估计 理想估计 -
[1] WANG Chengxiang, HUANG Jie, WANG Haiming, et al. 6G wireless channel measurements and models: Trends and challenges[J]. IEEE Vehicular Technology Magazine, 2020, 15(4): 22–32. doi: 10.1109/MVT.2020.3018436 [2] SAYED A, KHATUN M, AHMED T, et al. Performance analysis of OFDM system on multipath fading and inter symbol interference (ISI) using AWGN[M]. DAS A K, NAYAK J, NAIK B, et al. Computational Intelligence in Pattern Recognition. Singapore: Springer, 2022: 25–36. doi: 10.1007/978-981-16-2543-5_3. [3] JIANG T, CHEN H H, WU H C, et al. Channel modeling and inter-carrier interference analysis for V2V communication systems in frequency-dispersive channels[J]. Mobile Networks and Applications, 2010, 15(1): 4–12. doi: 10.1007/s11036-009-0177-2 [4] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. Proceedings of 2017 IEEE Wireless Communications and Networking Conference, San Francisco, USA, 2017: 1–6. [5] RAMACHANDRAN M K, SURABHI G D, and CHOCKALINGAM A. OTFS: A new modulation scheme for high-mobility use cases[J]. Journal of the Indian Institute of Science, 2020, 100(2): 315–336. doi: 10.1007/s41745-020-00167-4 [6] NAVEEN C and SUDHA V. Peak-to-average power ratio reduction in OTFS modulation using companding technique[C]. Proceedings of the 2020 5th International Conference on Devices, Circuits and Systems, Coimbatore, India, 2020: 140–143. doi: 10.1109/ICDCS48716.2020.243567. [7] LI Shuangyang, YUAN Jinhong, YUAN Weijie, et al. Performance analysis of coded OTFS systems over high-mobility channels[J]. IEEE Transactions on Wireless Communications, 2021, 20(9): 6033–6048. doi: 10.1109/TWC.2021.3071493 [8] RAVITEJA P, HONG Yi, VITERBO E, et al. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 957–961. doi: 10.1109/TVT.2018.2878891 [9] ZEMEN T, HOFER M, LÖSCHENBRAND D, et al. Iterative detection for orthogonal precoding in doubly selective channels[C]. Proceedings of the 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 2018: 1–7. doi: 10.1109/PIMRC.2018.8580716. [10] THAJ T, VITERBO E, and HONG Yi. Orthogonal time sequency multiplexing modulation: Analysis and low-complexity receiver design[J]. IEEE Transactions on Wireless Communications, 2021, 20(12): 7842–7855. doi: 10.1109/TWC.2021.3088479 [11] STOFFER D S. Walsh-Fourier analysis and its statistical applications[J]. Journal of the American Statistical Association, 1991, 86(414): 461–479. doi: 10.1080/01621459.1991.10475067 [12] HARMUTH H F. Applications of Walsh functions in communications[J]. IEEE Spectrum, 1969, 6(11): 82–91. doi: 10.1109/MSPEC.1969.5214175 [13] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011 [14] RAVITEJA P, PHAN K T, JIN Qianyu, et al. Low-complexity iterative detection for orthogonal time frequency space modulation[C]. Proceedings of 2018 IEEE Wireless Communications and Networking Conference, Barcelona, Spain, 2018: 1–6. doi: 10.1109/WCNC.2018.8377159. [15] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276 [16] LI Li, WEI Hua, HUANG Yao, et al. A simple two-stage equalizer with simplified orthogonal time frequency space modulation over rapidly time-varying channels[J]. arXiv: 1709.02505, 2017. [17] WALKER D W, ALDCROFT T, CISNEROS A, et al. LU decomposition of banded matrices and the solution of linear systems on hypercubes[C]. Proceedings of the Third Conference on Hypercube Concurrent Computers and Applications, Pasadena, USA, 1989: 1635–1655. doi: 10.1145/63047.63124. [18] BJÖRCK Å. Numerical Methods for Least Squares Problems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1996: 274–283. [19] SAAD Y. Iterative Methods for Sparse Linear Systems[M]. 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics, 2003: 95–116. [20] AHMADI S, SRINIVASAN R, CHOI H, et al. Channel models for IEEE 802.16 m evaluation methodology document[J]. IEEE 802. 16 Broadband Wireless Access Working Group, 2007: 03–12. -





 下载:
下载:
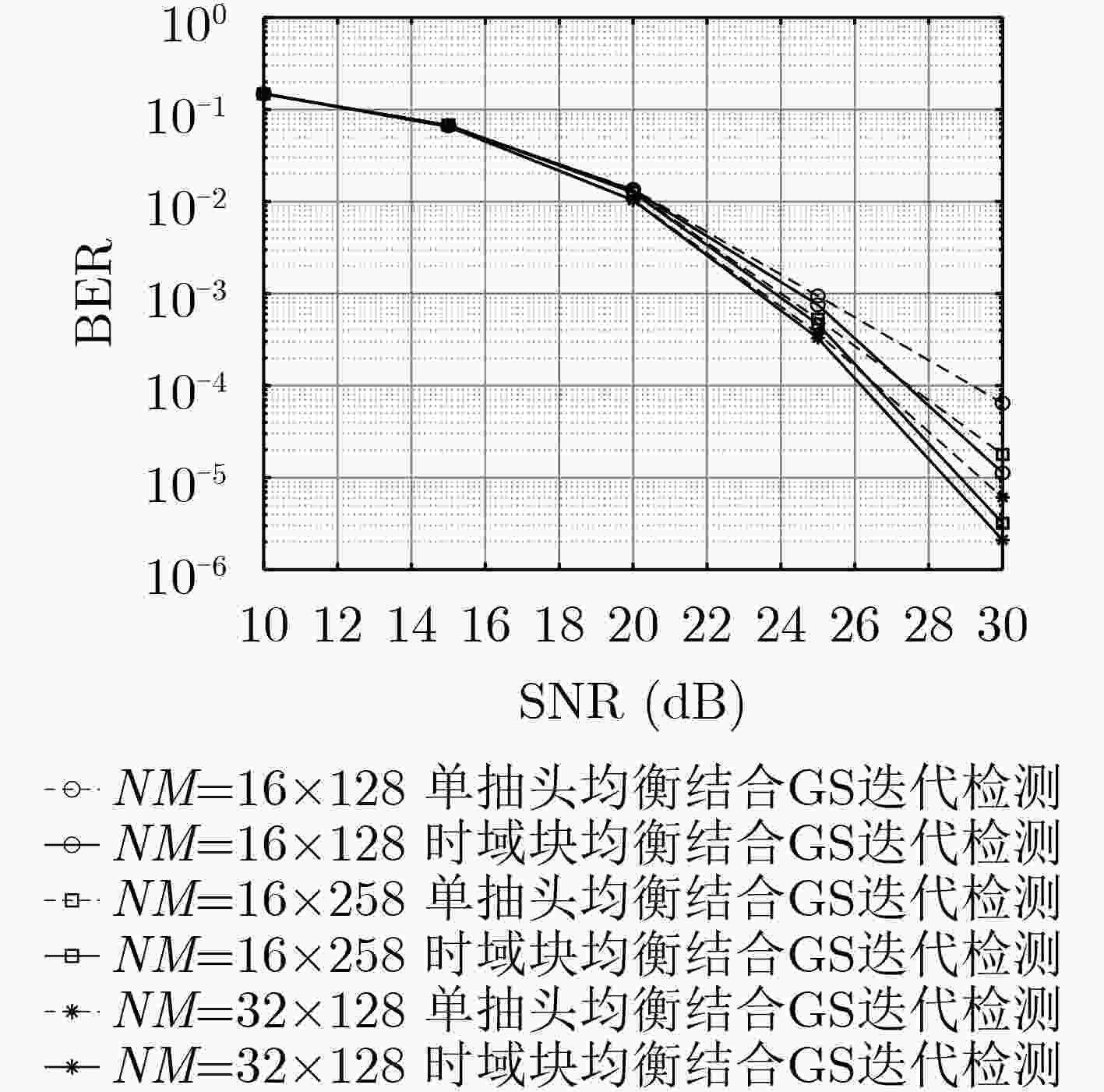
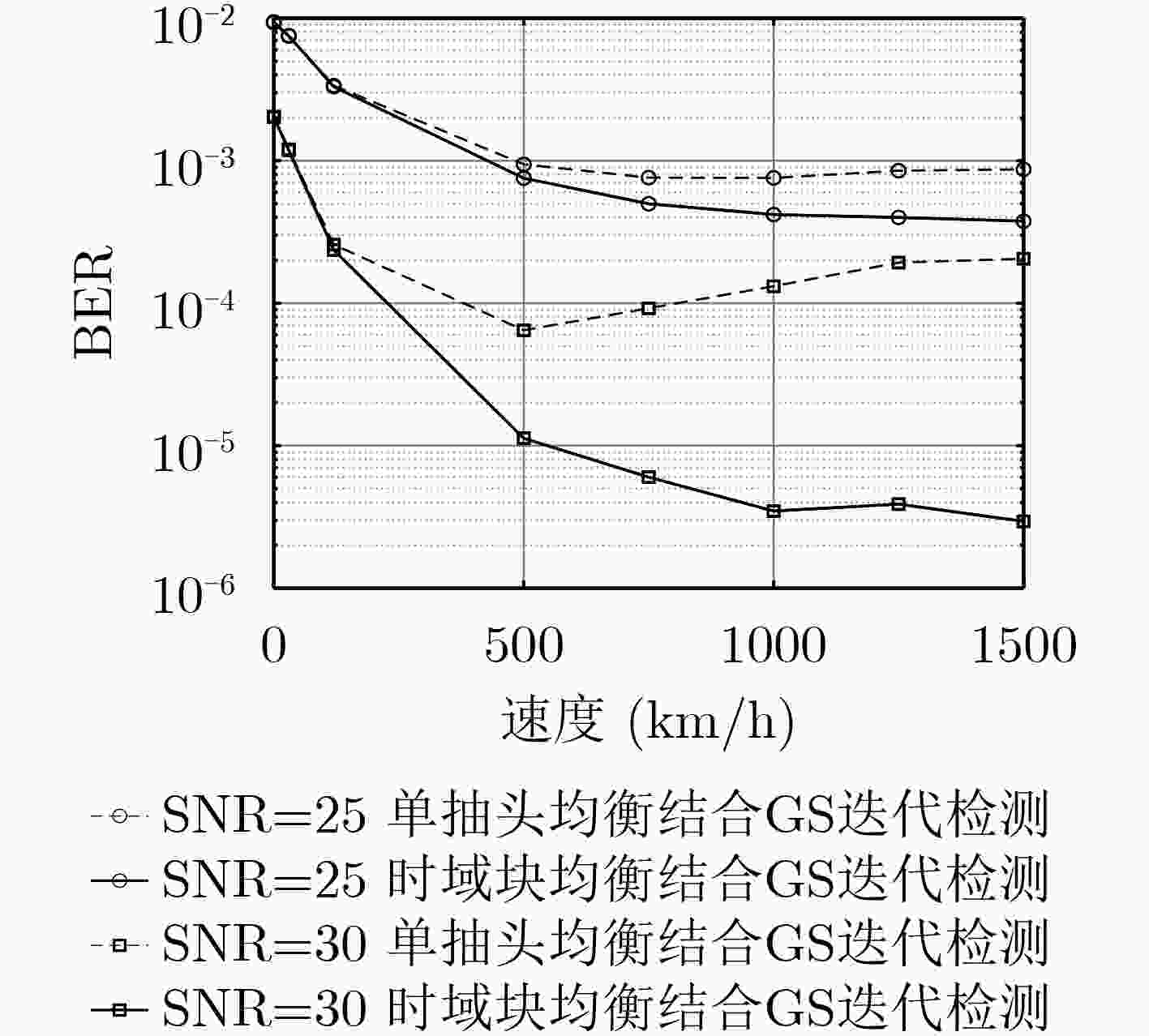
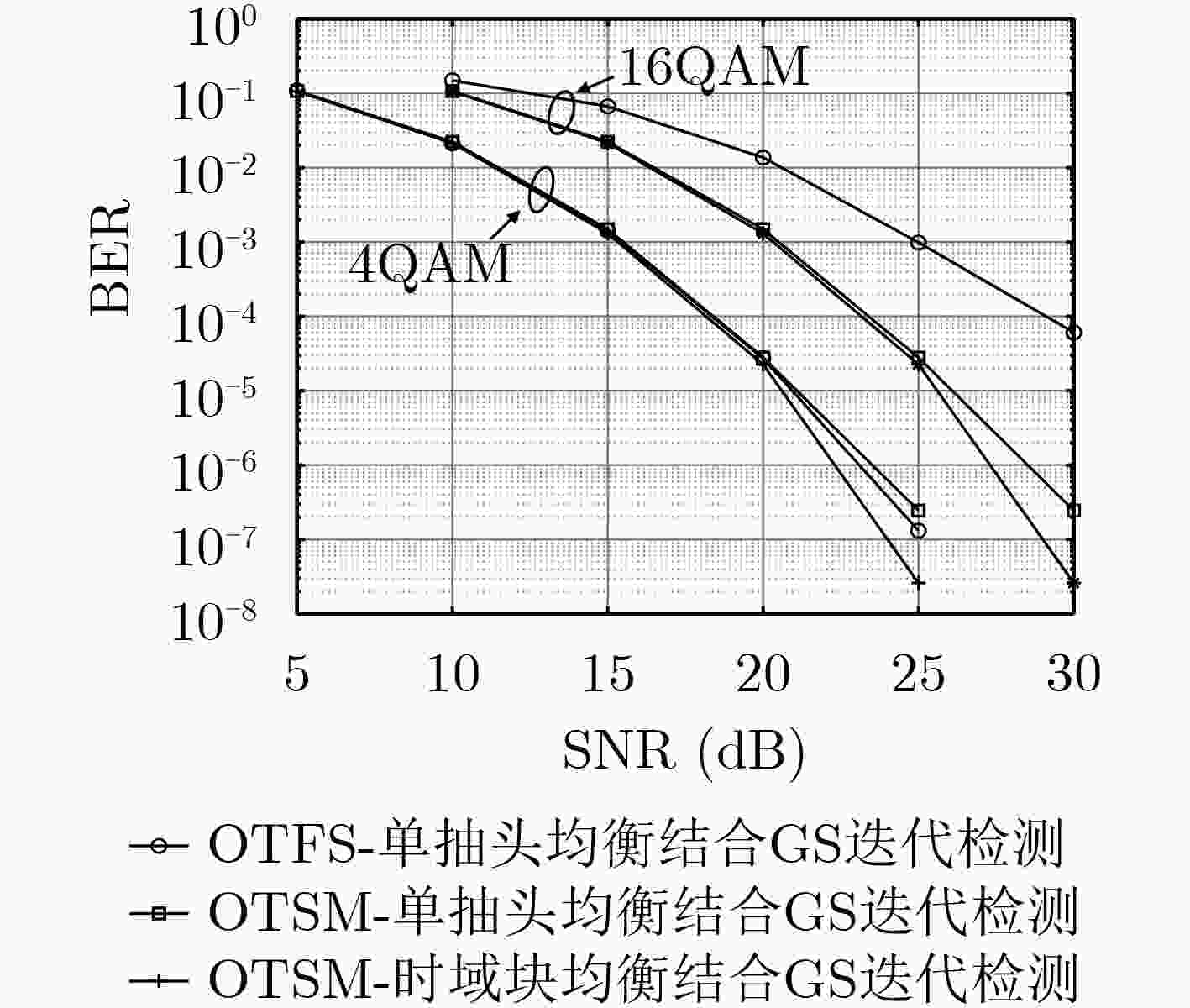
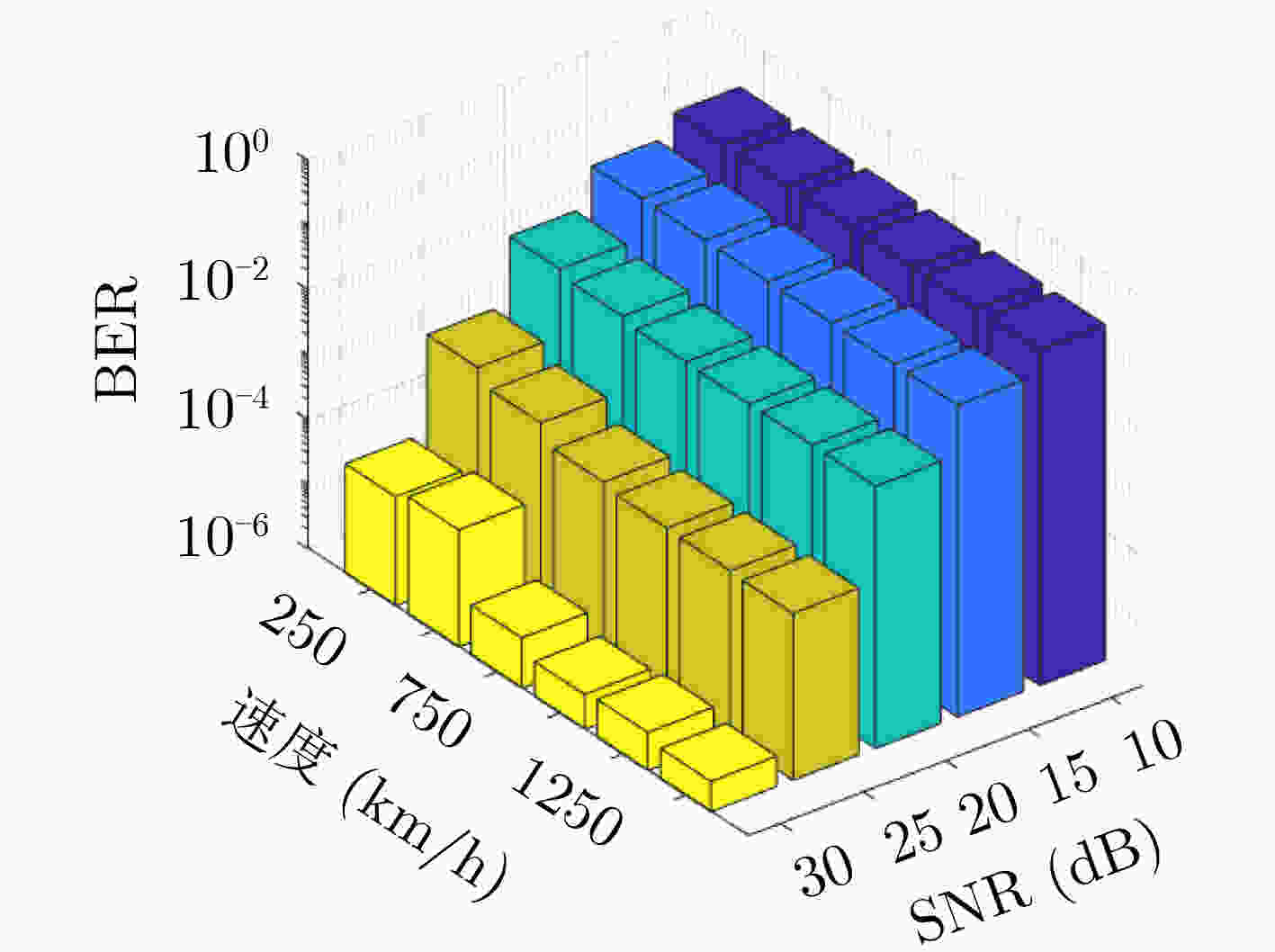


 下载:
下载:
