Traffic Shaping Mechanism Based on Time Slot-Aware Cyclic Queuing and Forwarding in Time-Sensitive Networking
-
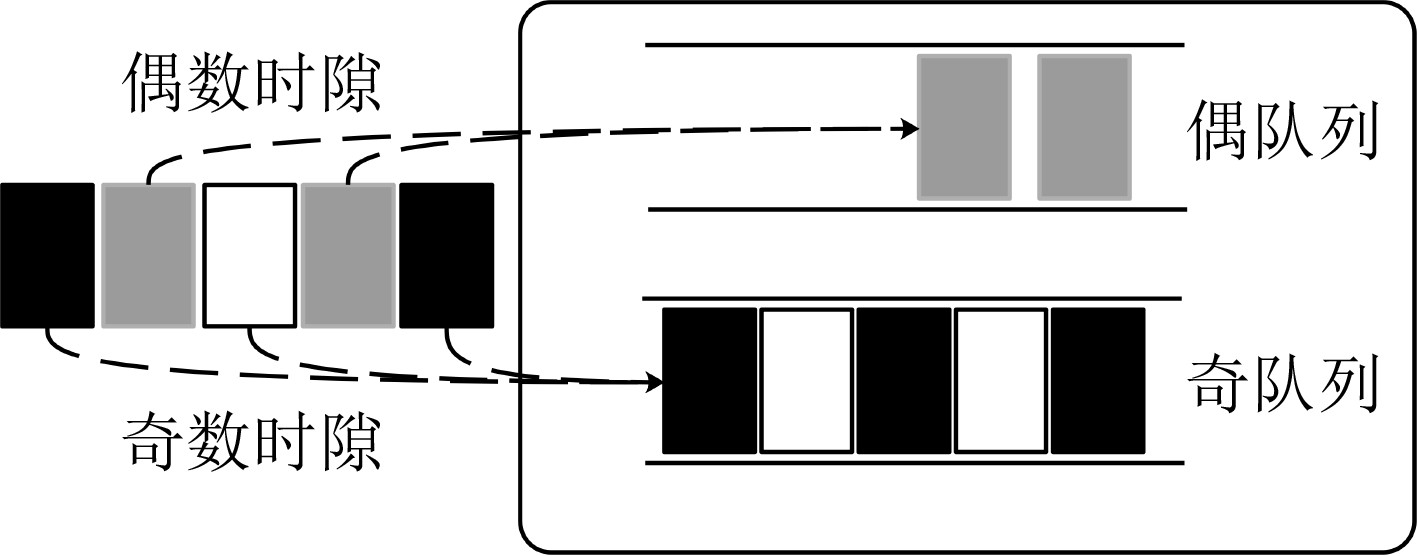
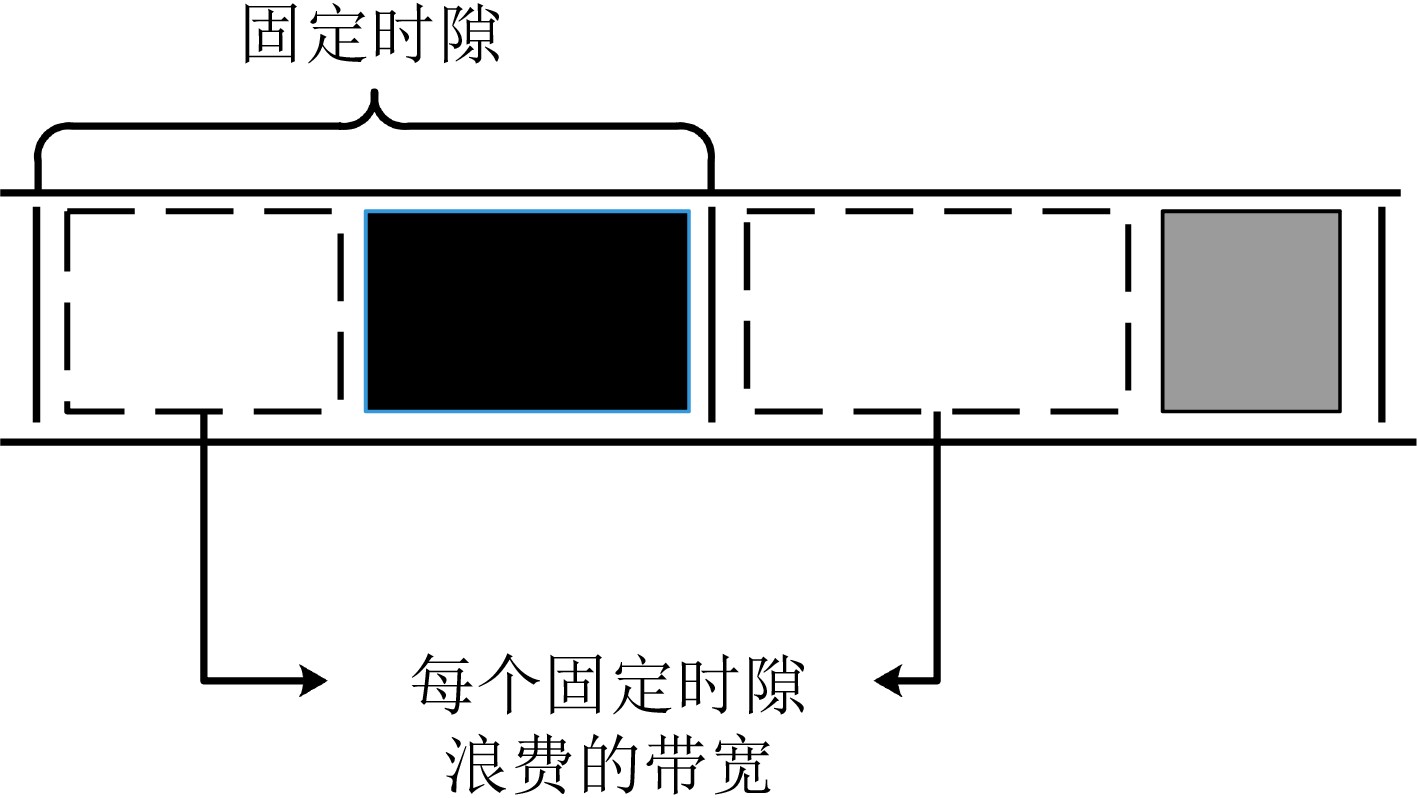
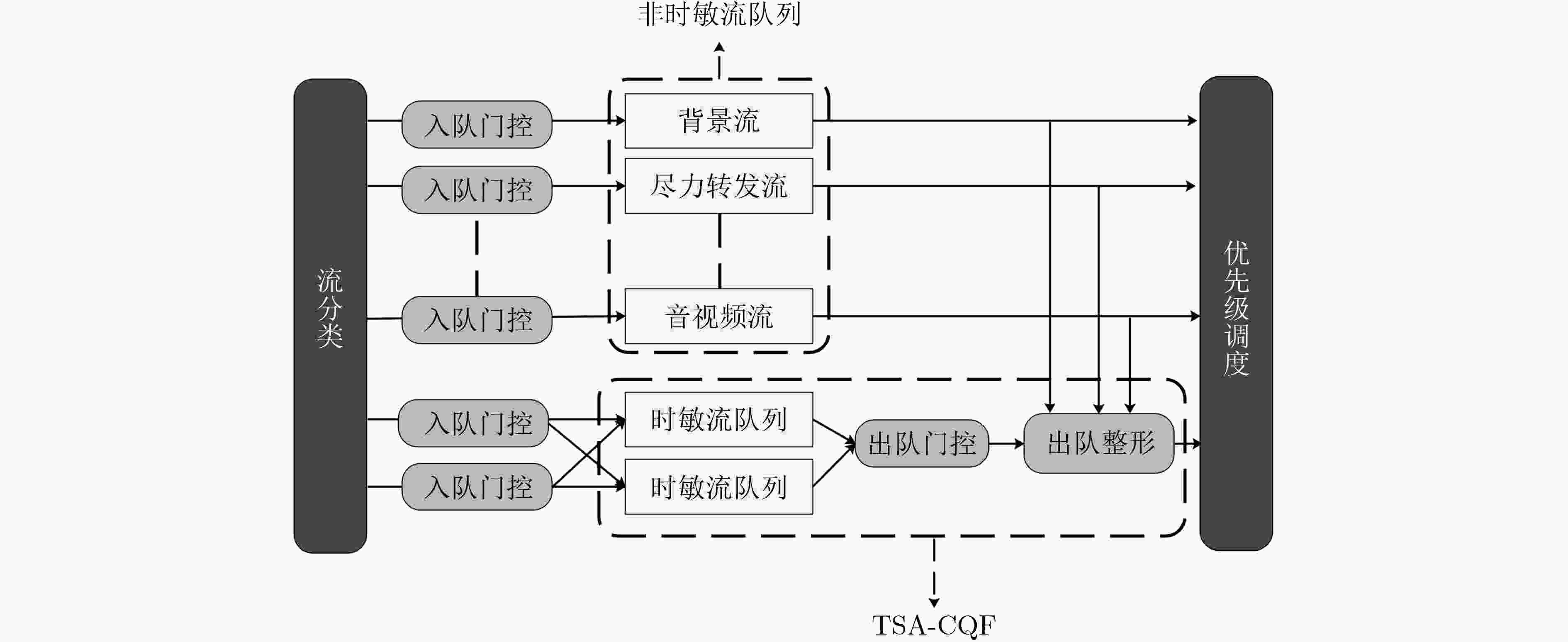
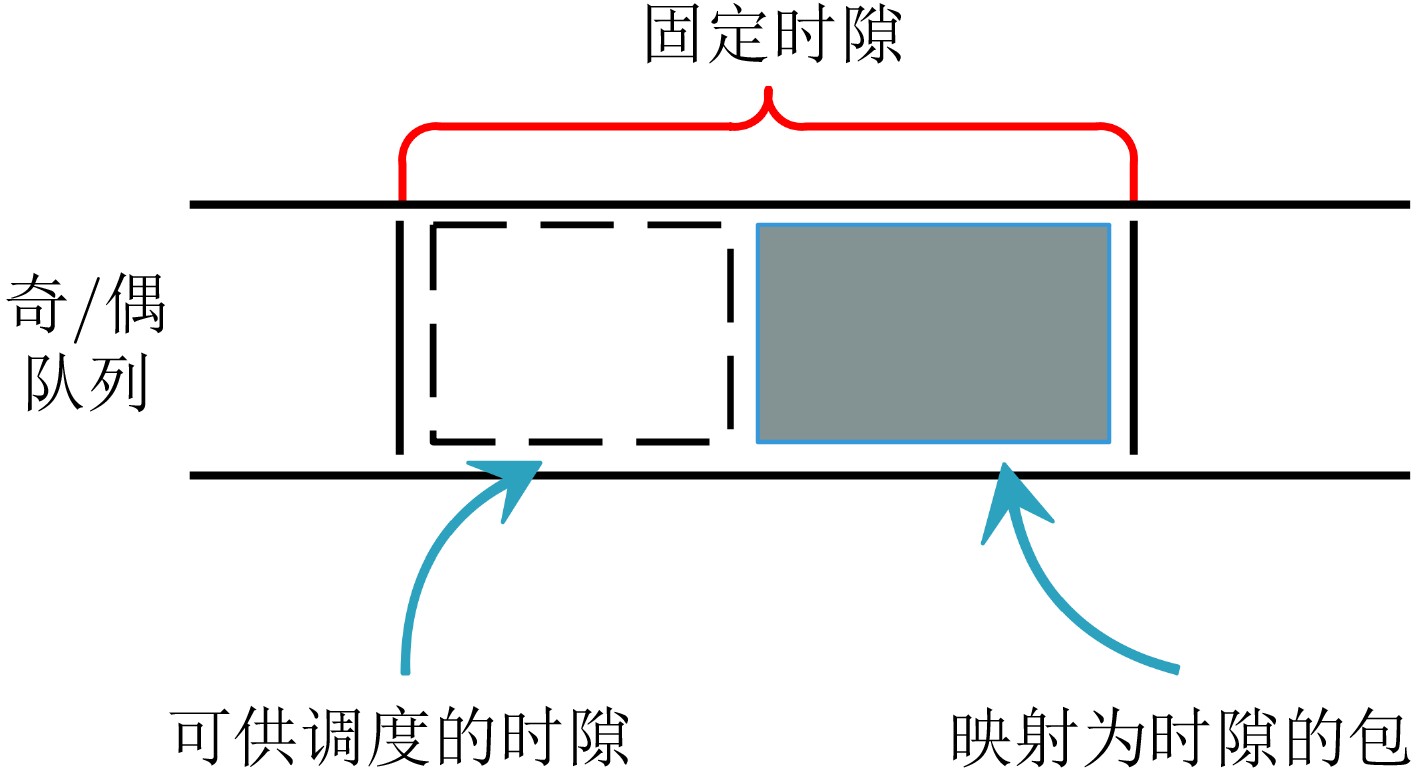
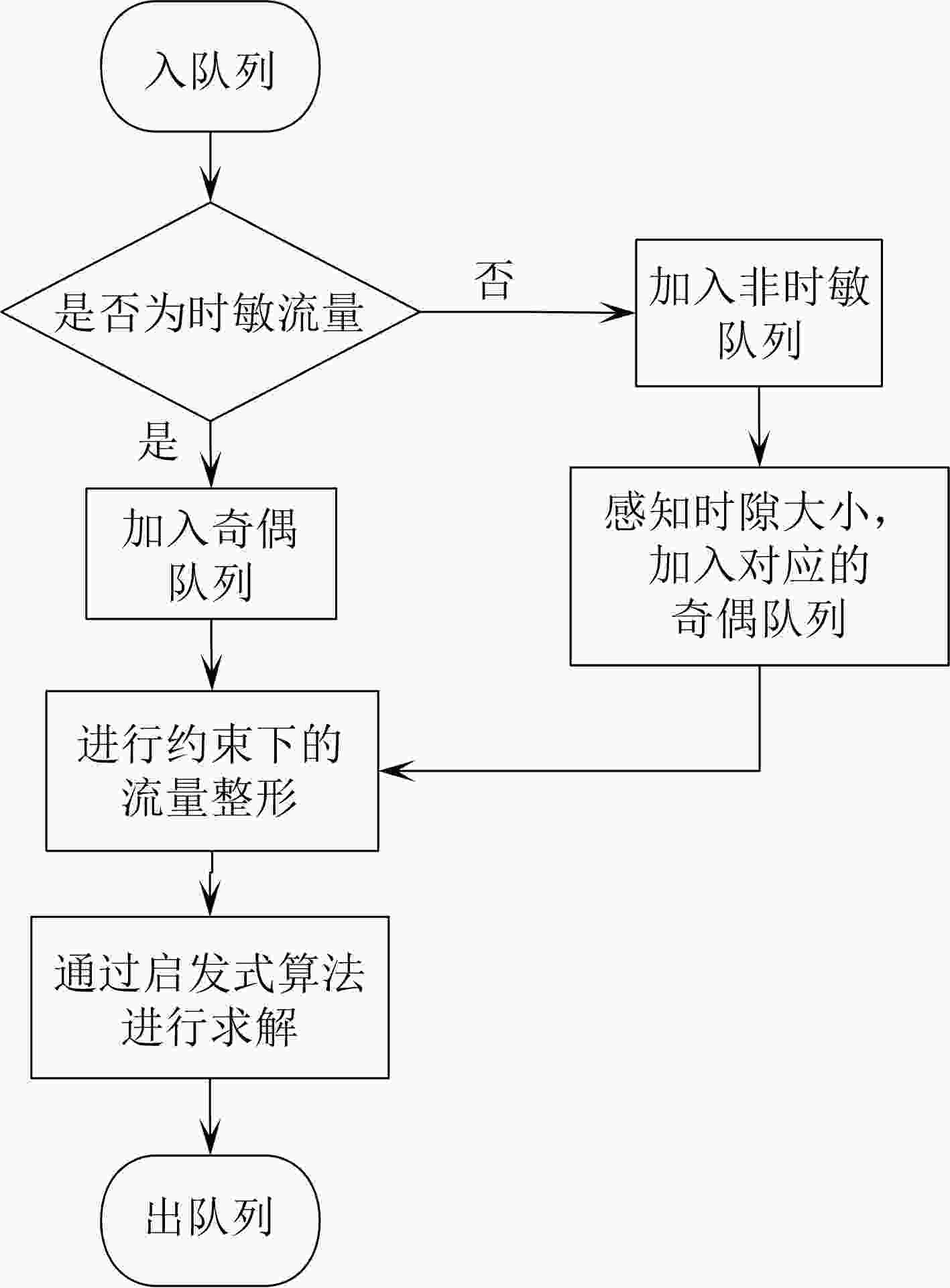
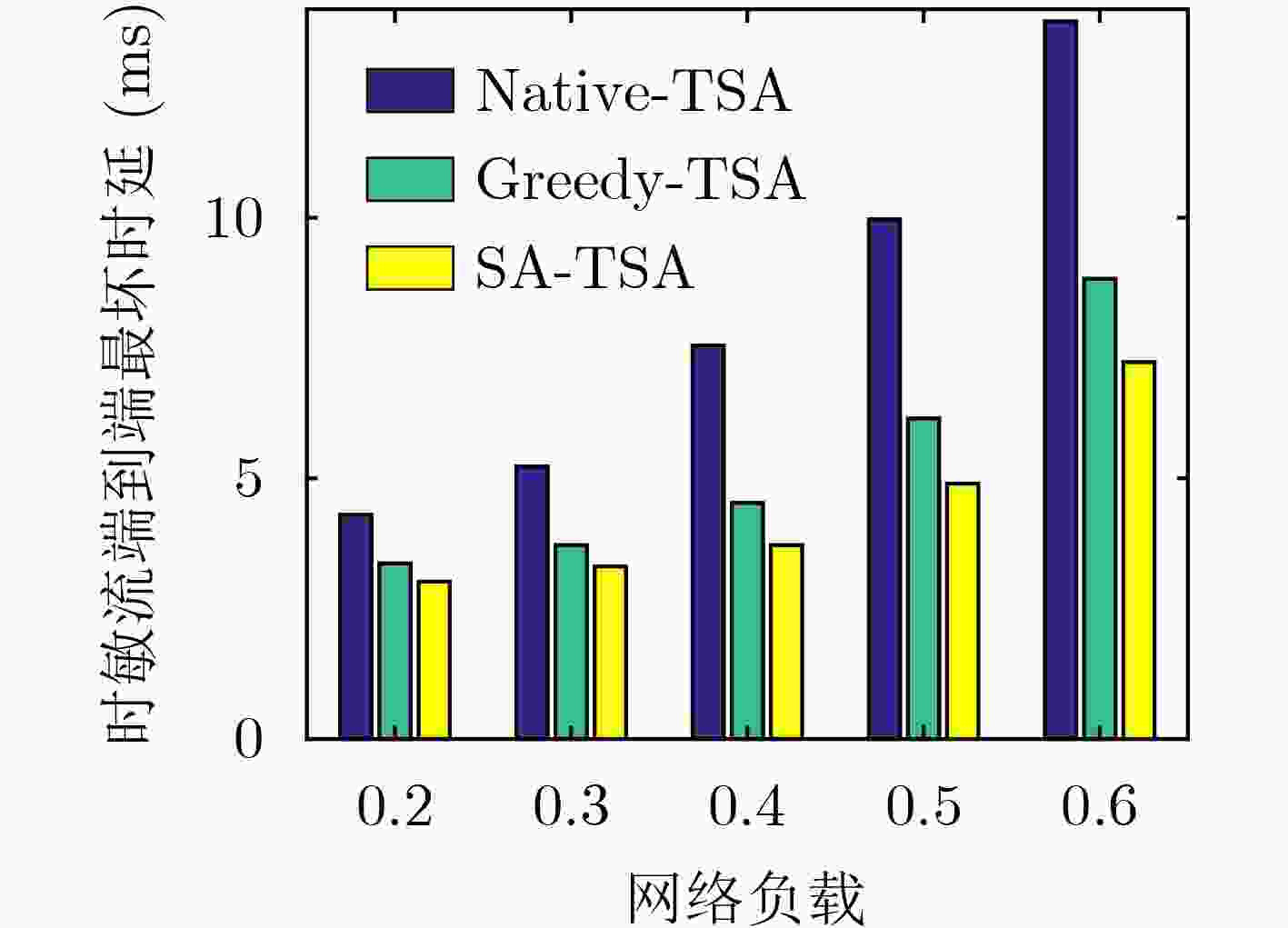
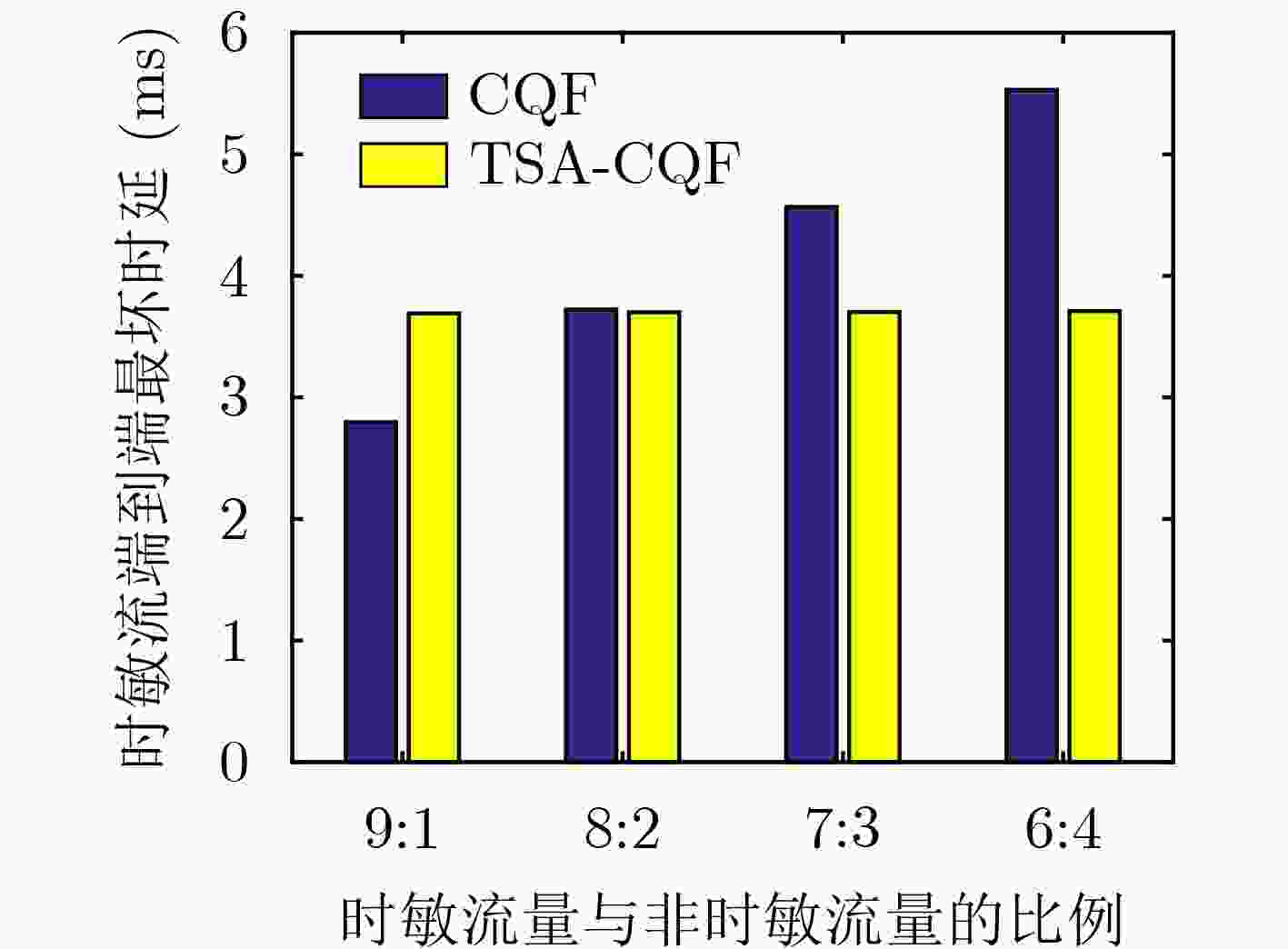
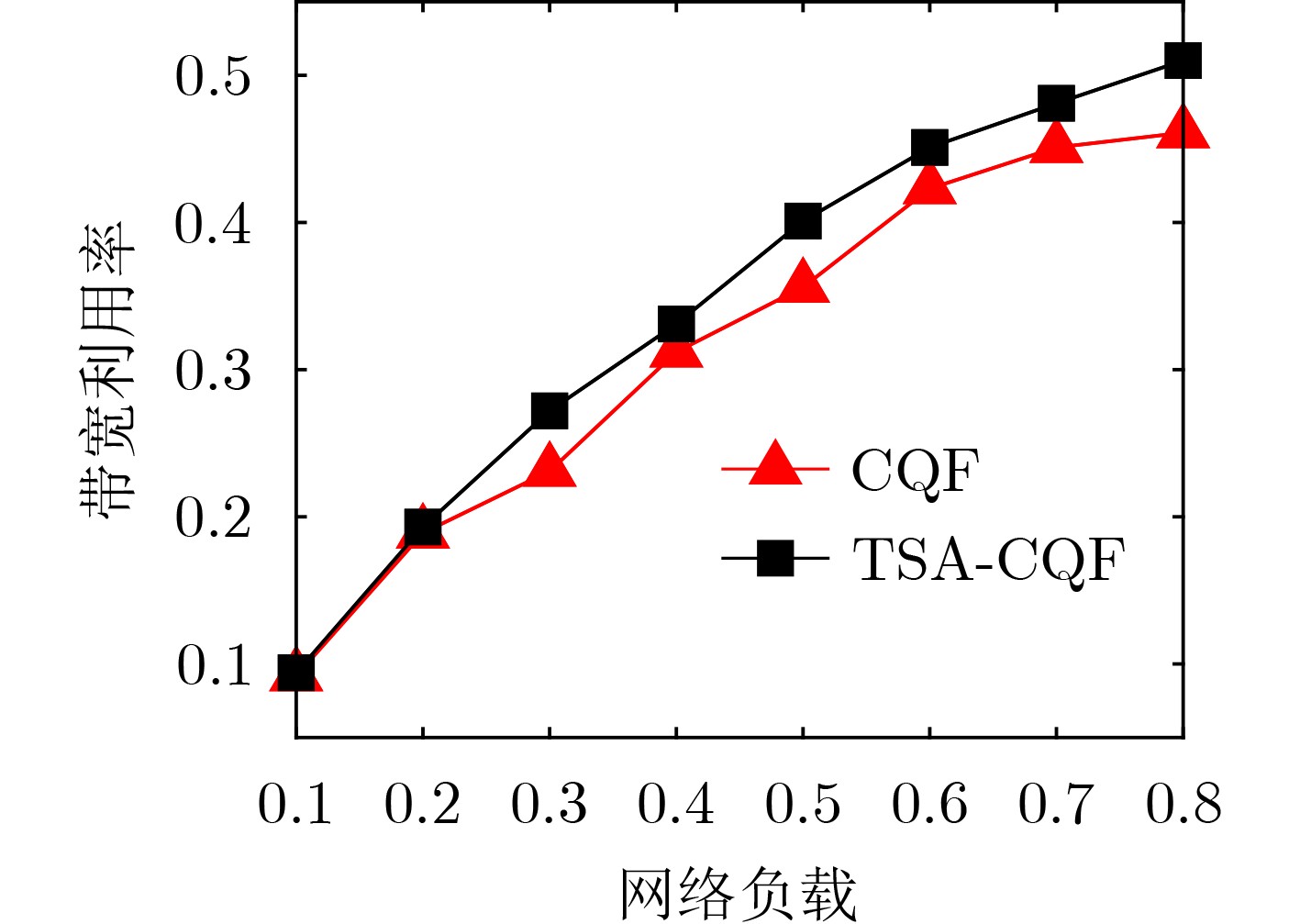
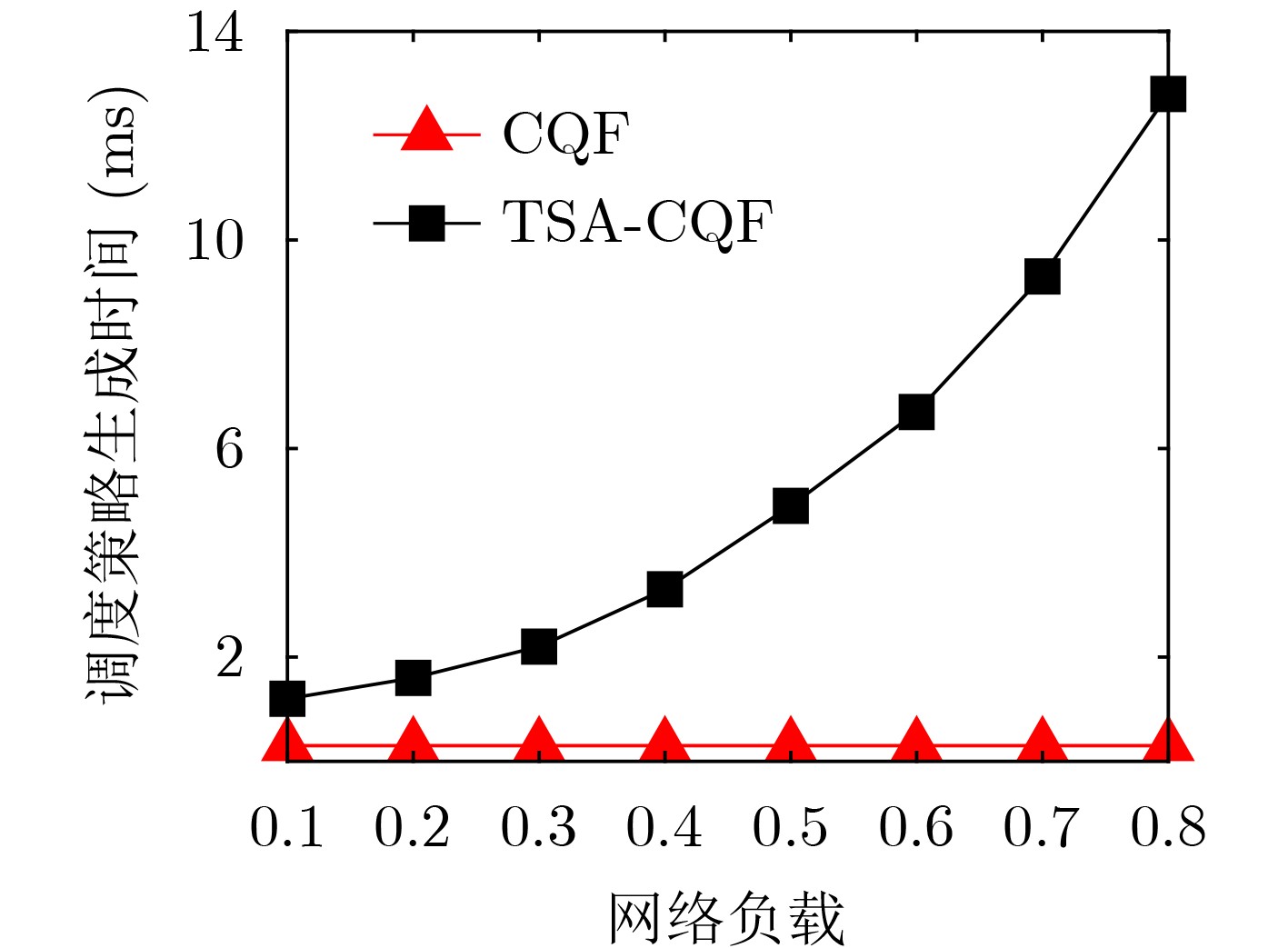
摘要: 时间敏感网络是智能工厂内网的核心技术之一。智能工厂内存在多种需求各异的业务流。为保证关键业务流的性能,同时提升网络带宽利用率,该文提出一种时隙感知循环排队转发流量整形机制(TSA-CQF)。TSA-CQF通过将低优先级流量插入CQF奇偶队列中剩余可用时隙中传输提高带宽利用率。TSA-CQF机制包括低优先级流量的时隙感知插入和全局流量规划两个部分。低优先级流量的时隙感知插入是在CQF队列出队时,通过感知奇偶队列剩余时隙的大小,将低优先级流量插入到奇偶队列的剩余时隙进行传输。将全局流量规划建模为多条件约束目标优化问题,通过模拟退火算法求解,完成全局流量的调度,提高可调度流数目,进一步提高资源利用率。仿真结果表明,在混合流量条件下TSA-CQF比传统CQF机制平均提高了带宽利用率11.29%。与传统的CQF相比,TSA-CQF在牺牲一定调度策略生成时间的前提下,能明显提高带宽利用率并且降低最坏端到端时延。Abstract: Time sensitive network is one of the core technologies of future smart factories. There are multiple business flows with different requirements in smart factories. To ensure the performance of critical traffic flows and improve network bandwidth utilization, a Time Slot-Aware Cyclic Queuing and Forwarding (TSA-CQF) mechanism is proposed. TSA-CQF improves bandwidth utilization by inserting low-priority traffic into the remaining available time slots of the CQF queues. TSA-CQF mechanism includes slot-aware insertion of low-priority traffic and global traffic planning for low-priority traffic. The first part of TSA-CQF is to insert low-priority traffic into the remaining time slots of the CQF queues. The global traffic planning is modeled as a multi-conditional objective optimization problem, and it is solved by the simulated annealing algorithm to accept as many flows as possible to increase the bandwidth utilization. Simulation results show that TSA-CQF improves the bandwidth utilization by 11.29% on average compared with the traditional CQF mechanism under mixed traffic conditions.
-
表 1 约束参数说明
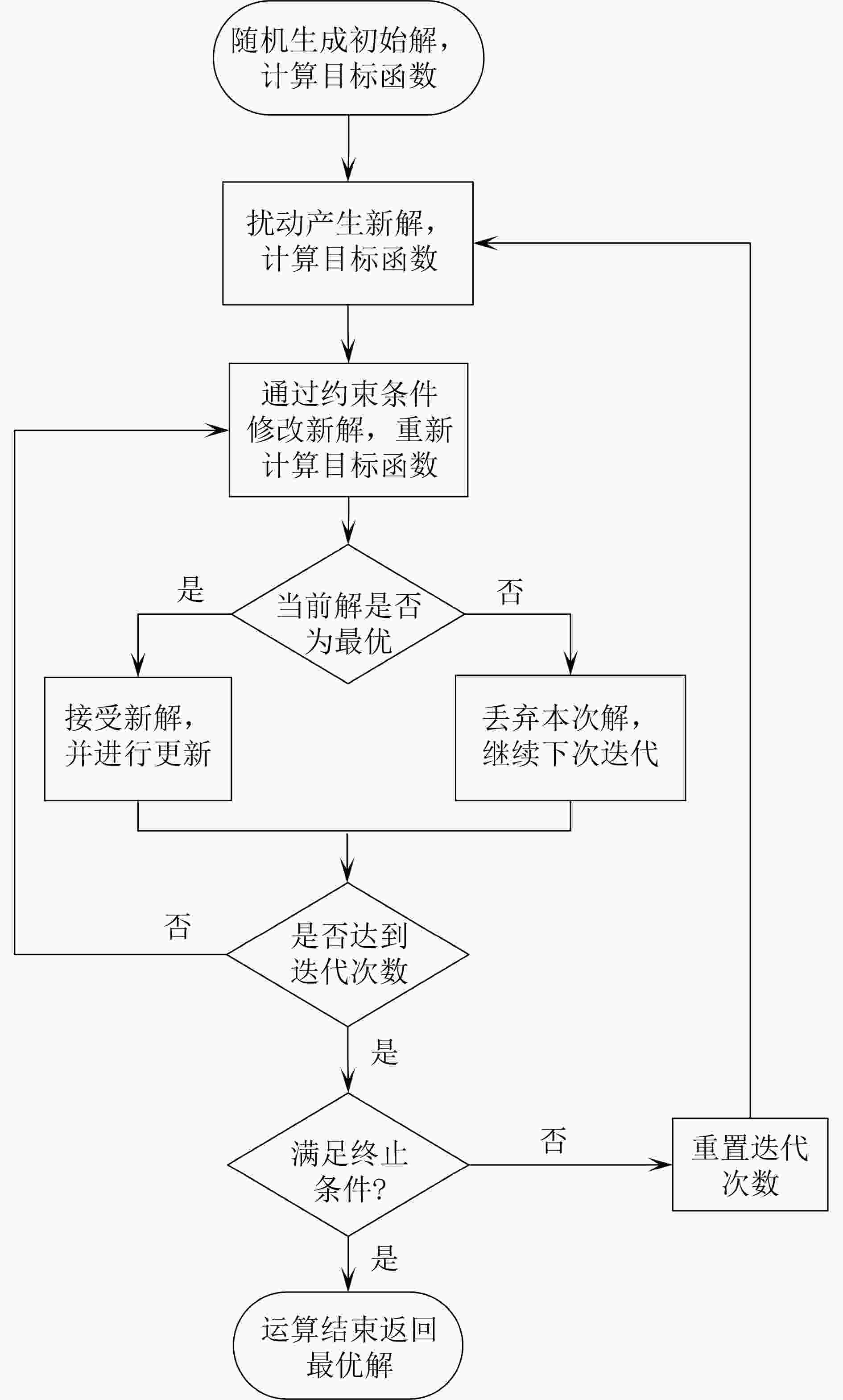
参数 描述 $S$ 流的集合 ${S_{[a,b]}}$ 流从发出节点a到接收节点b ${T_{{s_i}}}$ 最坏端到端时延 ${L_{{s_i}}}$ 数据大小(以字节为单位) ${C_{{s_i}}}$ 流的周期 ${f_{[a,b]}}$ 流中的帧从节点a到节点b ${f_{[a,b]}}{\text{ }} \cdot {\text{ }}\phi $ 流从节点a到b的帧映射到时钟上的偏移量 ${f_{[a,b]}}{\text{ }} \cdot {\text{ }}T$ 流从节点a到b的帧映射到时钟上的周期 ${f_{[a,b]}}{\text{ }} \cdot {\text{ }}L$ 流从节点a到b的帧映射到时钟上传输大小 ${F_{[{\text{a}},b]}}$ 流${S_{[a,b]}}$和帧${f_{[a,b]}}$的集合 算法1 SA-TSA 算法 输入:G //网络拓扑 F //流资源设置 Q //队列资源设置 Ri //流约束设置,i∈[1,5] 输出:Foffset //流偏移量 Fcur←{G,F,R}_init; //通过输入初始化当前解 for (i=0;i<N;i++) //循环每一个流 for (j=1;j<=5;j++) //循环每一个约束条件 if Fi contain Rj //判断是否满足约束条件 Qcur←Qfresh; //满足则更新可用资源数 Continue; else while Fi contain Rj //不满足则进行偏移循环 Fcur←F do offset; end while; end if end for end for while numcur <numitera AND Fi contain Ri //迭代 Fnew←SA random() compute; //扰动产生新解 if Fnew better than Fcur //对最优解进行更新 Fcur =Fnew ; end if numcur++; //当前迭代次数加1 end while return Fcur; //完成迭代,输出最优解 表 2 仿真参数
参数 分布 取值 链路带宽(Mbit/s) – 1 000 网络负载 – [0.1,1] 帧数量 – 5×104 帧大小(Byte) 均匀分布 [64,500] 帧到达过程 泊松分布 500 奇偶时隙大小(µs) – 250 队列长度(MByte) – 1 -
[1] NIKISHIN K and KONNOV N. Schedule time-triggered ethernet[C]. 2020 International Conference on Engineering Management of Communication and Technology, Vienna, Austria, 2020: 1–5. [2] LI Ziyang, ZHANG Yiming, ZHAO Yunxiang, et al. Efficient semantic-aware coflow scheduling for data-parallel jobs[C]. 2016 IEEE International Conference on Cluster Computing, Taipei, China, 2016: 154–155. [3] LI Ziyang, ZHANG Yiming, ZHAO Yunxiang, et al. Best effort task scheduling for data parallel jobs[C]. 2016 ACM SIGCOMM Conference, Florianopolis, Brazil, 2016: 555–556. [4] FINN N. Introduction to time-sensitive networking[J]. IEEE Communications Standards Magazine, 2018, 2(2): 22–28. doi: 10.1109/MCOMSTD.2018.1700076 [5] SAHOO S, BAO Ninghai, BIGO S, et al. Deterministic dynamic network-based just-in-time delivery for distributed edge computing[C]. 2020 European Conference on Optical Communications, Brussels, Belgium, 2020: 1–4. [6] IEEE. IEEE std 802.1QchTM-2017 IEEE standard for local and metropolitan area networks - bridges and bridged networks - amendment 29: Cyclic queuing and forwarding[S]. New York: IEEE, 2017. [7] IEEE. IEEE Std 802.1QbvTM-2015. IEEE standard for local and metropolitan area networks - bridges and bridged networks - amendment 25: Enhancements for scheduled traffic[S]. New York: IEEE, 2016. [8] GARDINER E. The Avnu alliance theory of operation for TSN-enabled industrial systems[J]. IEEE Communications Standards Magazine, 2018, 2(1): 5. doi: 10.1109/MCOMSTD.2018.8334911 [9] NASRALLAH A, THYAGATURU A S, ALHARBI Z, et al. Ultra-Low Latency (ULL) networks: The IEEE TSN and IETF DetNet standards and related 5G ULL research[J]. IEEE Communications Surveys & Tutorials, 2019, 21(1): 88–145. [10] MESSENGER J L. Time-sensitive networking: An introduction[J]. IEEE Communications Standards Magazine, 2018, 2(2): 29–33. doi: 10.1109/MCOMSTD.2018.1700047 [11] BIGO S, BENZAOUI N, CHRISTODOULOPOULOS K, et al. Dynamic deterministic digital infrastructure for time-sensitive applications in factory floors[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2021, 27(6): 6000314. doi: 10.1109/JSTQE.2021.3093281 [12] FINN N, LE BOUDEC J Y, MOHAMMADPOUR E, et al. DetNet bounded latency[EB/OL]. https://datatracker.ietf.org/doc/draft-ietf-detnet-bounded-latency/, 2022. [13] SEAMAN M. Paternoster policing and scheduling[EB/OL]. https://grouper.ieee.org/groups/802/1/files/public/docs2017/cr-seaman-paternoster-policing-scheduling-0317-v03.pdf, 2017. [14] YAN Jinli, WEI Quan, JIANG Xuyan, et al. Injection time planning: Making CQF practical in time-sensitive networking[C]. 2020 IEEE Conference on Computer Communications, Toronto, Canada, 2020: 616–625. [15] HUANG Yudong, WANG Shuo, WU Binwei, et al. TACQ: Enabling zero-jitter for cyclic-queuing and forwarding in time-sensitive networks[C]. 2021 IEEE International Conference on Communications, Montreal, Canada, 2021: 1–6. [16] WANG Guangjun, XU Caifeng, and LIU Gang. The transient electromagnetic inversion based on the simplex-simulated annealing algorithm[C]. The 37th Chinese Control Conference, Wuhan, China, 2018: 4321–4324. [17] 谢维, 关嘉欣, 周游, 等. 基于改进模拟退火算法的登机口分配问题[J]. 计算机系统应用, 2021, 30(5): 157–163. doi: 10.15888/j.cnki.csa.007903XIE Wei, GUAN Jiaxin, ZHOU You, et al. Gate distribution problem based on improved simulated annealing algorithm[J]. Computer Systems &Applications, 2021, 30(5): 157–163. doi: 10.15888/j.cnki.csa.007903 [18] YERA Y G, LILLO R E, NIELSEN B F, et al. A bivariate two-state Markov modulated Poisson process for failure modeling[J]. Reliability Engineering & System Safety, 2021, 208: 107318. doi: 10.1016/j.ress.2020.107318 -





 下载:
下载:


 下载:
下载:
