基于迭代交替优化的图像盲超分辨率重建

陈洪刚; 李自强; 张永飞; 王正勇; 卿粼波; 何小海

doi:10.11999/JEIT220380

基于迭代交替优化的图像盲超分辨率重建

doi: 10.11999/JEIT220380

四川大学电子信息学院成都 610065

基金项目: 国家自然科学基金(62001316, 61871279)，四川省自然科学基金(2022NSFSC0922)，中央高校基本科研业务费专项资金(2021SCU12061)

详细信息

作者简介:
陈洪刚：男，副研究员，研究方向为图像与视频处理

李自强：男，硕士生，研究方向为图像超分辨率重建

张永飞：男，硕士生，研究方向为图像超分辨率重建

王正勇：女，副教授，研究方向为图像与视频处理

卿粼波：男，教授，研究方向为图像与视频处理

何小海：男，教授，研究方向为图像与视频处理

通讯作者:
王正勇　wangzheny@scu.edu.cn

中图分类号: TN911.73; TP391
计量
- 文章访问数: 836
- HTML全文浏览量: 466
- PDF下载量: 255
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-01
- 修回日期: 2022-05-21
- 网络出版日期: 2022-07-01
- 刊出日期: 2022-10-19

Blind Image Super-resolution Reconstruction via Iterative and Alternative Optimization

College of Electronics and Information Engineering, Sichuan University, Chengdu 610065, China

Funds: The National Natural Science Foundation of China (62001316, 61871279), The Natural Science Foundation of Sichuan Province (2022NSFSC0922), The Fundamental Research Foundation for the Central Universities (2021SCU12061)

摘要

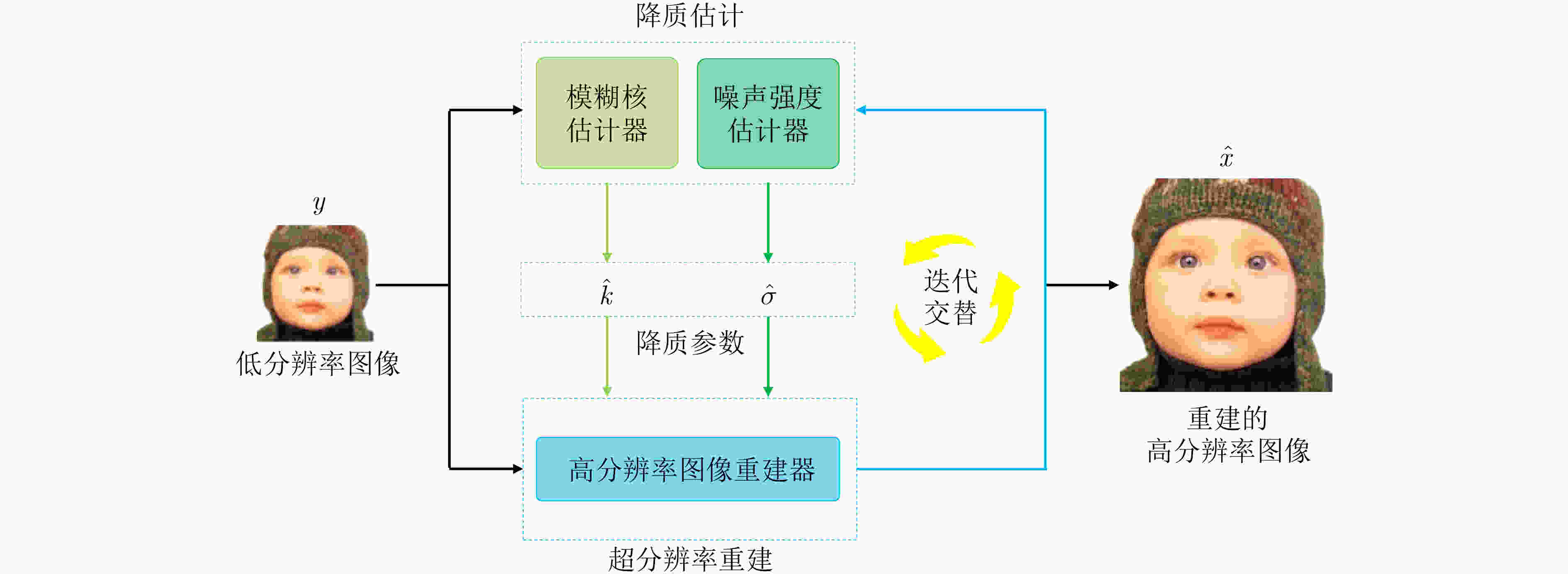
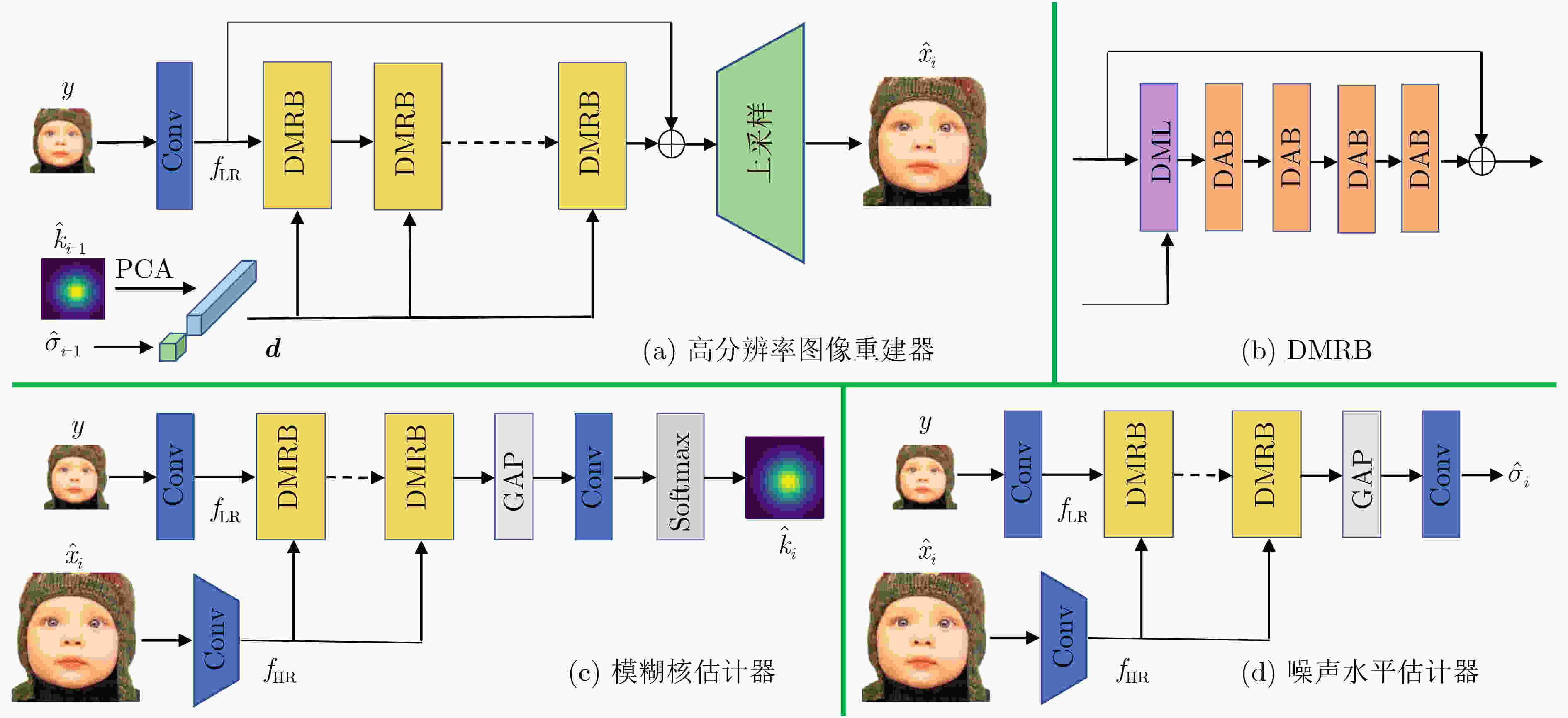
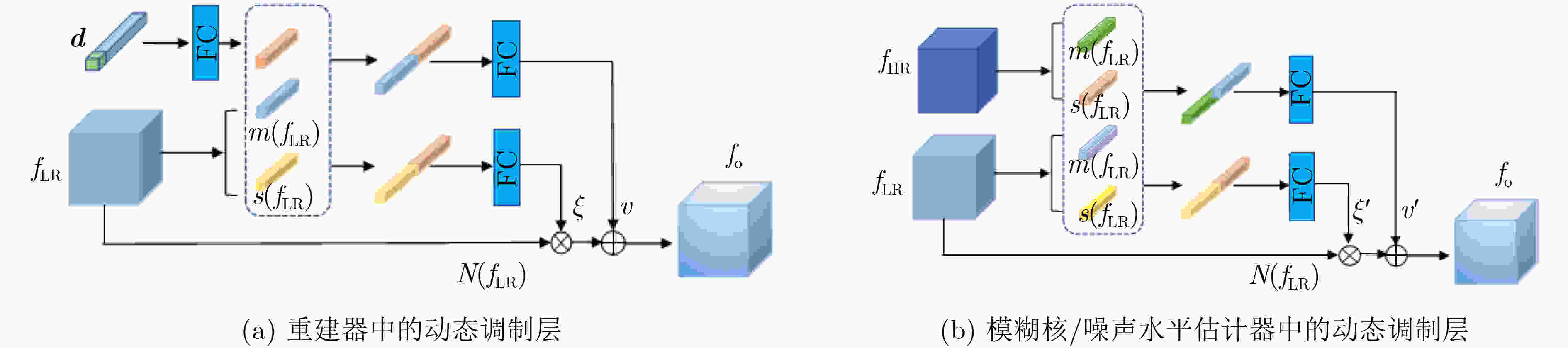
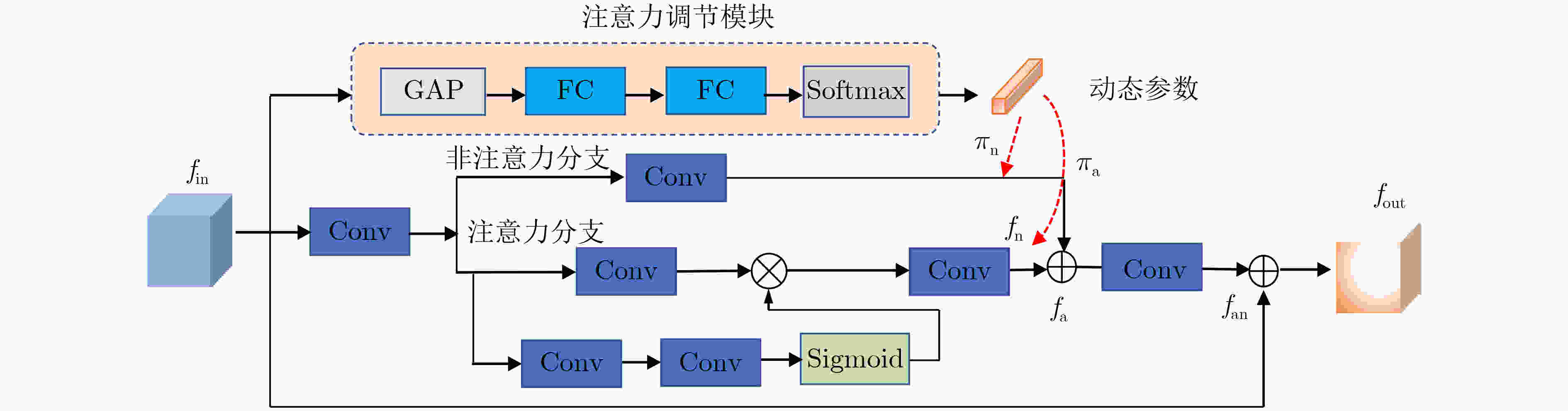
摘要: 基于深度卷积神经网络的图像超分辨率重建算法通常假设低分辨率图像的降质是固定且已知的，如双3次下采样等，因此难以处理降质(如模糊核及噪声水平)未知的图像。针对此问题，该文提出联合估计模糊核、噪声水平和高分辨率图像，设计了一种基于迭代交替优化的图像盲超分辨率重建网络。在所提网络中，图像重建器以估计的模糊核和噪声水平作为先验信息，由低分辨率图像重建出高分辨率图像；同时，综合低分辨率图像和估计的高分辨率图像，模糊核及噪声水平估计器分别实现模糊核和噪声水平的估计。进一步地，该文提出对模糊核/噪声水平估计器及图像重建器进行迭代交替的端对端优化，以提高它们的兼容性并使其相互促进。实验结果表明，与IKC, DASR, MANet, DAN等现有算法相比，提出方法在常用公开测试集(Set5, Set14, B100, Urban100)及真实场景图像上都取得了更优的性能，能够更好地对降质未知的图像进行重建；同时，提出方法在参数量或处理效率上也有一定的优势。
- 图像盲超分辨率重建 /
- 卷积神经网络 /
- 模糊核估计 /
- 噪声水平估计 /
- 迭代交替优化
Abstract: Deep convolutional neural network-based image Super-Resolution (SR) methods assume generally that the degradations of Low-Resolution (LR) images are fixed and known (e.g., bicubic downsampling). Thus, they are almost unable to super-resolve images with unknown degradations (e.g., blur kernel and noise level). To address this problem, an iterative and alternative optimization-based blind image SR network is proposed, in which the blur kernel, noise level, and High-Resolution (HR) image are jointly estimated. Specifically, in the proposed method, the image reconstruction network reconstructs an HR image from the given LR image using the estimated blur kernel and noise level as prior knowledge. Correspondingly, the blur kernel and noise level estimators estimate the blur kernel and noise level respectively from the given LR image and the reconstructed HR image. To improve compatibility and promote each other mutually, the blur kernel estimator, noise level estimator, and image reconstruction network are iteratively and alternatively optimized in an end-to-end manner. The proposed network is compared with state-of-the-art methods (i.e., IKC, DASR, MANet, DAN) on commonly used benchmarks (i.e., Set5, Set14, B100, and Urban100) and real-world images. Results show that the proposed method achieves better performance on LR images with unknown degradations. Moreover, the proposed method has advantages in model size or processing efficiency.
- Blind image super-resolution reconstruction /
- Convolutional neural network /
- Blur kernel estimation /
- Noise level estimation /
- Iterative and alternative optimization

HTML全文

图 1 提出算法的原理框图

下载: 全尺寸图片幻灯片

图 2 构建的图像重建器、模糊核估计器及噪声水平估计器的网络结构

下载: 全尺寸图片幻灯片

图 3 动态调制层(DML)

下载: 全尺寸图片幻灯片

图 4 动态注意力模块(DAB)

下载: 全尺寸图片幻灯片

图 5 不同算法对Urban100中“img097”图像的重建结果

下载: 全尺寸图片幻灯片

图 6 不同算法对真实场景图像“chip”的重建结果(重建尺度为4)

下载: 全尺寸图片幻灯片

图 7 Set5中图像的重建结果、模糊核估计及噪声水平估计随迭代次数的动态变化过程

下载: 全尺寸图片幻灯片

图 8 不同迭代次数下对Set5中“baby”图像的重建结果

下载: 全尺寸图片幻灯片

图 9 参数量与运行时间

下载: 全尺寸图片幻灯片

表 1 2倍重建结果的客观参数PSNR(dB)/SSIM比较

方法	噪声水平	Set5^[27]	Set14^[28]	B100^[29]	Urban100^[30]
Bicubic	5	30.07/0.8442	27.61/0.7620	27.23/0.7262	24.61/0.7253
Bicubic	10	28.85/0.7709	26.85/0.6979	26.51/0.6601	24.19/0.6637
MANet^[12]	5	33.60/0.9101	30.53/0.8407	29.45/0.8056	28.31/0.8513
MANet^[12]	10	32.15/0.8871	29.42/0.8048	28.40/0.7629	27.31/0.8202
DASR^[14]	5	33.35/0.9078	30.22/0.8325	29.12/0.7947	27.66/0.8364
DASR^[14]	10	31.95/0.8855	29.21/0.8003	28.21/0.7563	26.89/0.8107
DnCNN^[31]+IKC^[15]	5	31.69/0.8824	29.27/0.8118	28.67/0.7826	26.79/0.8089
DnCNN^[31]+IKC^[15]	10	30.85/0.8652	28.53/0.7817	27.90/0.7463	26.12/0.7830
DAN^[17]	5	33.83/0.9132	30.69/0.8430	29.52/0.8081	28.62/0.8566
DAN^[17]	10	32.32/0.8902	29.53/0.8072	28.45/0.7650	27.56/0.8256
本文算法	5	33.98/0.9153	30.85/0.8492	29.66/0.8140	28.79/0.8609
本文算法	10	32.39/0.8912	29.64/0.8110	28.54/0.7683	27.68/0.8283

下载: 导出CSV

表 2 4倍重建结果的客观参数PSNR(dB)/SSIM比较

方法	噪声水平	Set5^[27]	Set14^[28]	B100^[29]	Urban100^[30]
Bicubic	5	25.84/0.7162	24.29/0.6144	24.53/0.5825	21.70/0.5644
Bicubic	10	25.30/0.6728	23.91/0.5768	24.12/0.5438	21.48/0.5286
MANet^[12]	5	29.01/0.8242	26.59/0.6983	26.01/0.6507	24.01/0.6922
MANet^[12]	10	27.77/0.7928	25.74/0.6672	25.37/0.6207	23.36/0.6605
DASR^[14]	5	28.85/0.8214	26.46/0.6966	25.94/0.6494	23.72/0.6880
DASR^[14]	10	27.73/0.7921	25.69/0.6676	25.32/0.6207	23.16/0.6605
DnCNN^[31]+IKC^[15]	5	27.26/0.7619	25.51/0.6604	25.38/0.6218	22.92/0.6332
DnCNN^[31]+IKC^[15]	10	26.65/0.7493	25.03/0.6390	24.96/0.6008	22.53/0.6140
DAN^[17]	5	29.01/0.8238	26.62/0.6980	26.02/0.6507	24.02/0.6903
DAN^[17]	10	27.84/0.7947	25.85/0.6698	25.39/0.6223	23.44/0.6630
本文算法	5	29.32/0.8300	26.82/0.7060	26.16/0.6584	24.29/0.7036
本文算法	10	28.05/0.7999	25.98/0.6738	25.48/0.6260	23.61/0.6712

下载: 导出CSV

参考文献(31)

[1]	蔡文郁, 张美燕, 吴岩, 等. 基于循环生成对抗网络的超分辨率重建算法研究[J]. 电子与信息学报, 2022, 44(1): 178–186. doi: 10.11999/JEIT201046 CAI Wenyu, ZHANG Meiyan, WU Yan, et al. Research on cyclic generation countermeasure network based super-resolution image reconstruction algorithm[J]. Journal of Electronics &Information Technology, 2022, 44(1): 178–186. doi: 10.11999/JEIT201046
[2]	ZHANG Xiangjun and WU Xiaolin. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation[J]. IEEE Transactions on Image Processing, 2008, 17(6): 887–896. doi: 10.1109/TIP.2008.924279
[3]	ZHANG Kaibing, GAO Xinbo, TAO Dacheng, et al. Single image super-resolution with non-local means and steering kernel regression[J]. IEEE Transactions on Image Processing, 2012, 21(11): 4544–4556. doi: 10.1109/TIP.2012.2208977
[4]	DONG Chao, LOY C C, HE Kaiming, et al. Learning a deep convolutional network for image super-resolution[C]. Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 184–199.
[5]	CHEN Hanting, WANG Yunhe, GUO Tianyu, et al. Pre-trained image processing transformer[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 12299–12310.
[6]	LIANG Jingyun, CAO Jiezhang, SUN Guolei, et al. SwinIR: Image restoration using swin transformer[C]. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops, Montreal, Canada, 2021: 1833–1844.
[7]	ZHANG Kai, LIANG Jingyun, VAN GOOL L, et al. Designing a practical degradation model for deep blind image super-resolution[C]. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 4791–4800.
[8]	WANG Xintao, XIE Liangbin, DONG Chao, et al. Real-ESRGAN: Training real-world blind super-resolution with pure synthetic data[C]. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 1905–1914.
[9]	BELL-KLIGLER S, SHOCHER A, and IRANI M. Blind super-resolution kernel estimation using an internal-GAN[C]. Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 284–293.
[10]	LIANG Jingyun, ZHANG Kai, GU Shuhang, et al. Flow-based kernel prior with application to blind super-resolution[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 10601–10610.
[11]	TAO Guangpin, JI Xiaozhong, WANG Wenzhuo, et al. Spectrum-to-kernel translation for accurate blind image super-resolution[C/OL]. Advances in Neural Information Processing Systems, 2021: 34.
[12]	LIANG Jingyun, SUN Guolei, ZHANG Kai, et al. Mutual affine network for spatially variant kernel estimation in blind image super-resolution[C]. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 4096–4105.
[13]	KIM J, JUNG C, and KIM C. Dual back-projection-based internal learning for blind super-resolution[J]. IEEE Signal Processing Letters, 2020, 27: 1190–1194. doi: 10.1109/LSP.2020.3005043
[14]	WANG Longguang, WANG Yingqian, DONG Xiaoyu, et al. Unsupervised degradation representation learning for blind super-resolution[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 10581–10590.
[15]	GU Jinjin, LU Hannan, ZUO Wangmeng, et al. Blind super-resolution with iterative kernel correction[C]. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 1604–1613.
[16]	LUO Zhengxiong, HUANG Yan, LI Shang, et al. Unfolding the alternating optimization for blind super resolution[C/OL]. Advances in Neural Information Processing Systems, 2020: 5632–5643.
[17]	LUO Zhengxiong, HUANG Yan, LI Shang, et al. End-to-end alternating optimization for blind super resolution[EB/OL]. https://arxiv.org/abs/2105.06878v1, 2021.
[18]	WANG Zhihao, CHEN Jian, and HOI S C H. Deep learning for image super-resolution: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(10): 3365–3387. doi: 10.1109/TPAMI.2020.2982166
[19]	CHEN Honggang, HE Xiaohai, QING Linbo, et al. Real-world single image super-resolution: A brief review[J]. Information Fusion, 2022, 79: 124–145. doi: 10.1016/j.inffus.2021.09.005
[20]	LIU Anran, LIU Yihao, GU Jinjin, et al. Blind image super-resolution: A survey and beyond[EB/OL]. https://arxiv.org/abs/2107.03055, 2021.
[21]	HUI Zheng, LI Jie, WANG Xiumei, et al. Learning the non-differentiable optimization for blind super-resolution[C]. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 2093–2102.
[22]	CHEN Haoyu, GU Jinjin, and ZHANG Zhi. Attention in attention network for image super-resolution[EB/OL]. https://arxiv.org/abs/2104.09497v3, 2021.
[23]	GUO Shi, YAN Zifei, ZHANG Kai, et al. Toward convolutional blind denoising of real photographs[C]. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 1712–1722.
[24]	AGUSTSSON E and TIMOFTE R. NTIRE 2017 challenge on single image super-resolution: Dataset and study[C]. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, USA, 2017: 126–135.
[25]	TIMOFTE R, AGUSTSSON E, VAN GOOL L, et al. NTIRE 2017 challenge on single image super-resolution: Methods and results[C]. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, USA, 2017: 114–125.
[26]	KINGMA D P and BA J. ADAM: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2014.
[27]	BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]. British Machine Vision Conference, Surrey, United Kingdom, 2012.
[28]	ZEYDE R, ELAD M, and PROTTER M. On single image scale-up using sparse-representations[C]. 7th International Conference on Curves and Surfaces, Avignon, France, 2010: 711–730.
[29]	MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]. Proceedings Eighth IEEE International Conference on Computer Vision, Vancouver, Canada, 2001: 416–423.
[30]	HUANG J B, SINGH A, and AHUJA N. Single image super-resolution from transformed self-exemplars[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 5197–5206.
[31]	ZHANG Kai, ZUO Wangmeng, CHEN Yunjin, et al. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142–3155. doi: 10.1109/TIP.2017.2662206