A Digital Predistortion Technique Based on Improved Sparse Least Squares Twin Support Vector Regression
-
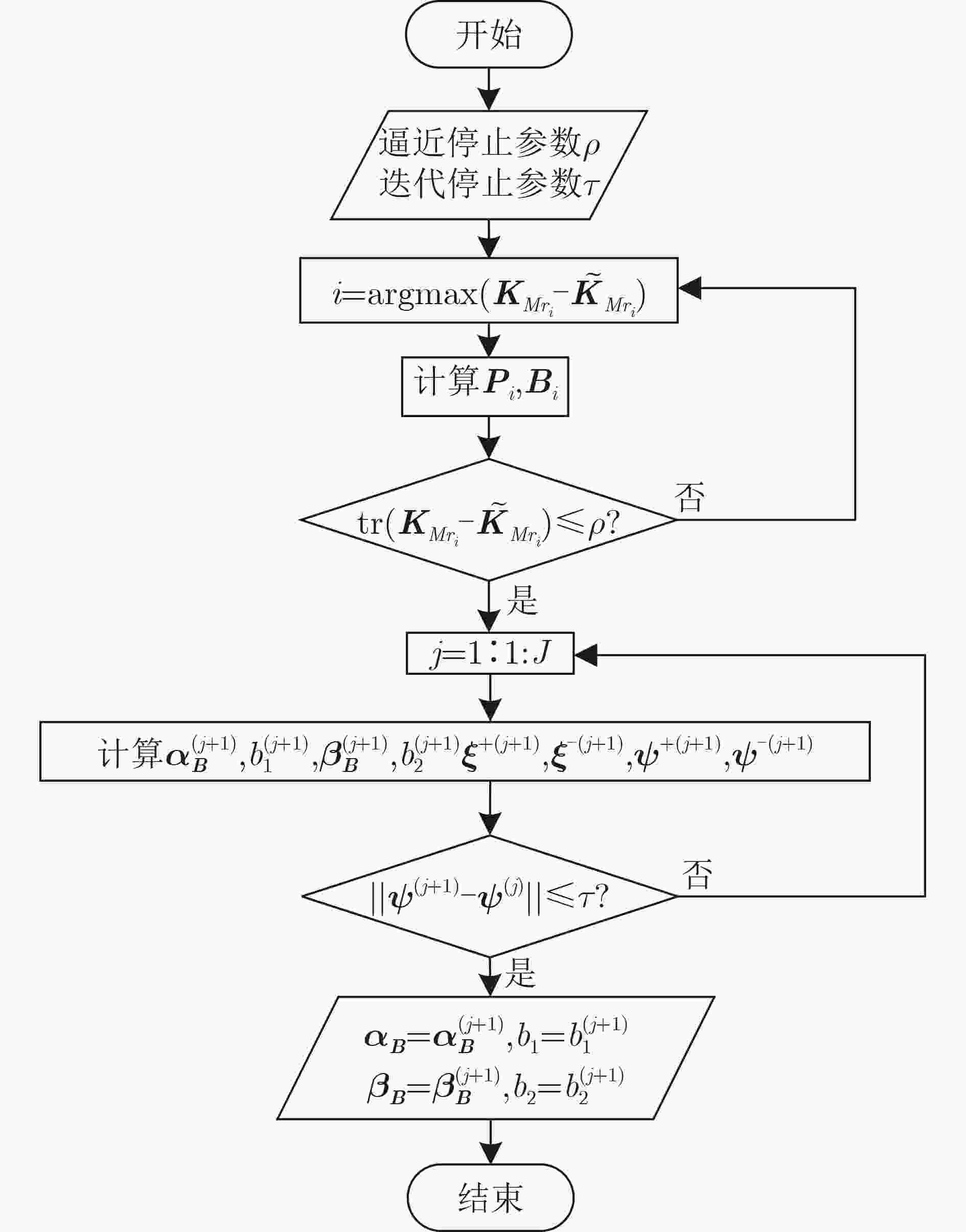
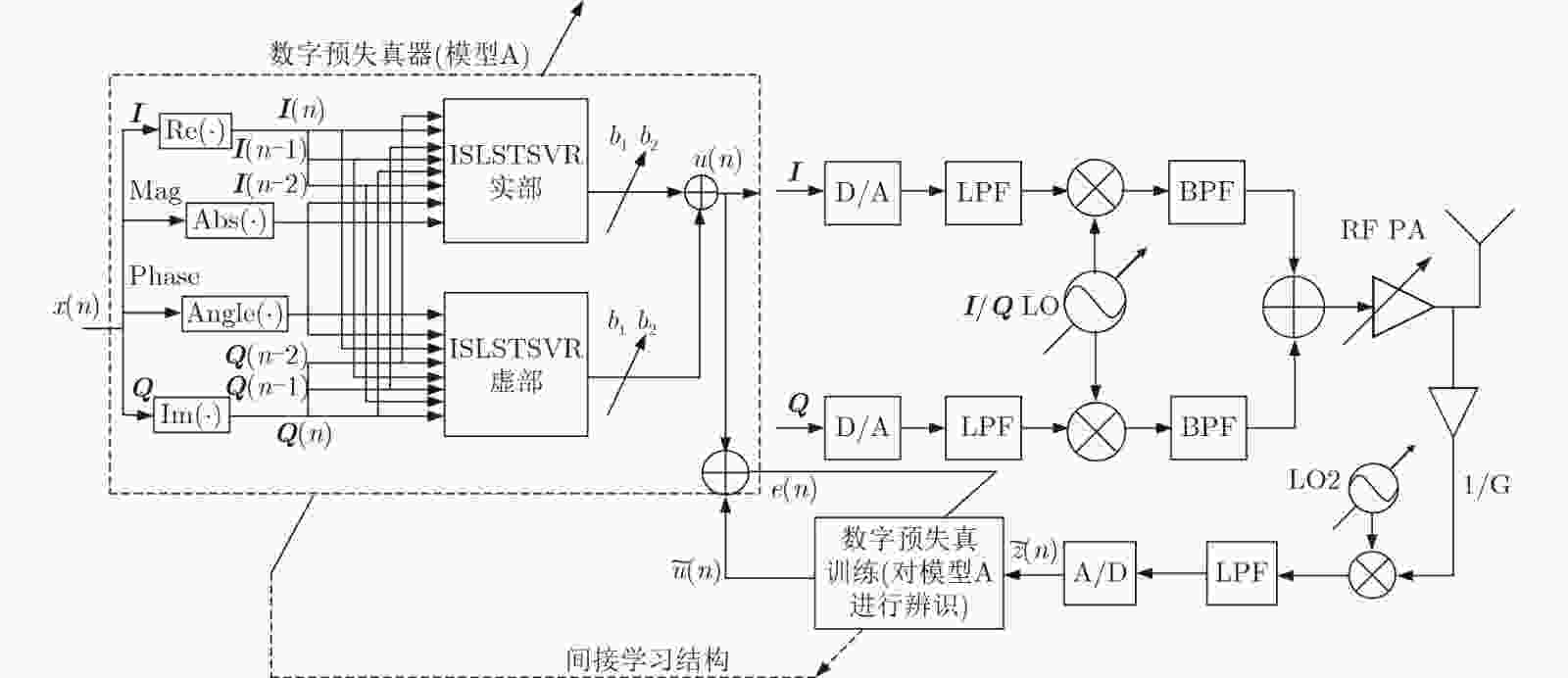
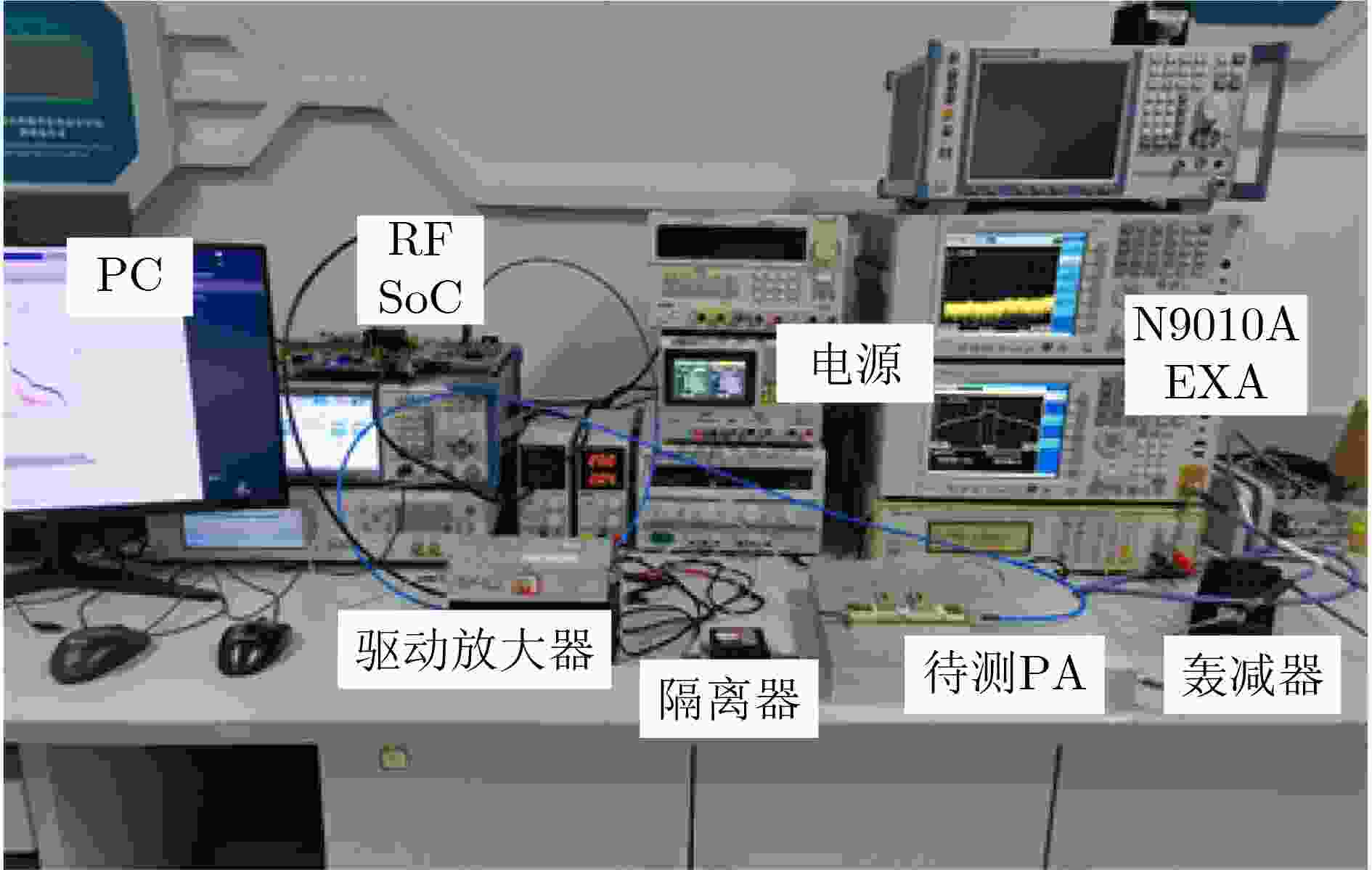
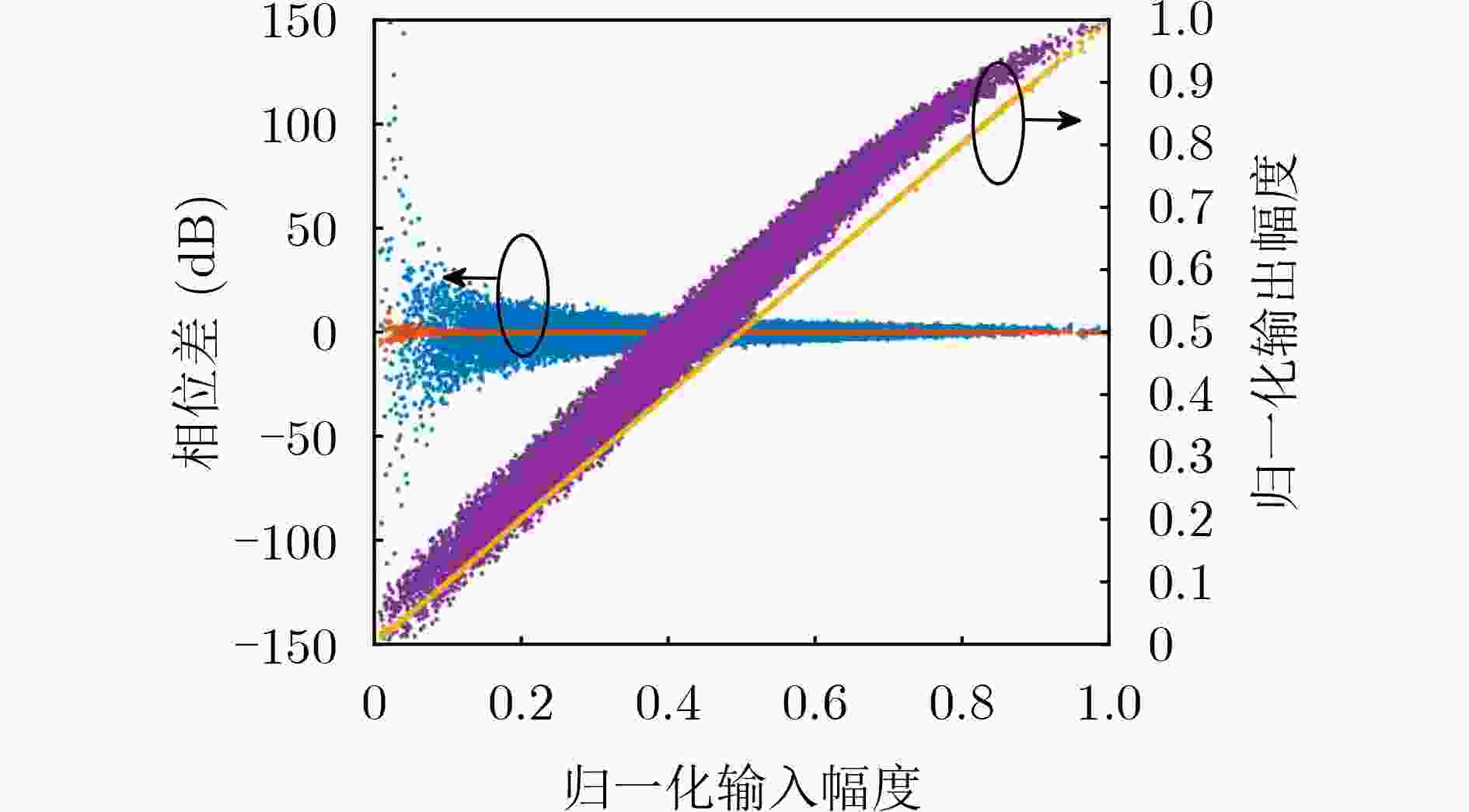
摘要: 为了补偿大容量卫星通信射频前端的功率放大器的非线性,传统的数字预失真(DPD)模型需要更多的系数和更高的阶次,严重影响预失真前馈路径的资源消耗。为了解决这一问题,该文提出一种基于改进的稀疏最小二乘双子支撑向量回归(ISLSTSVR)的低复杂度DPD方法。首先通过构建原空间的决策函数解决最小二乘双子支撑向量回归(LSTSVR)模型解不稀疏的问题;同时引用截断最小二乘损失函数增加模型的鲁棒性;然后采用Nystrom逼近方法得到核矩阵的低秩近似,进一步采用Cholesky分解降低核矩阵的运算复杂度;最后由低秩的核矩阵求得模型稀疏解。实验选用基于单管氮化镓(GaN)器件的宽带AB类功率放大器,以40 MHz的32QAM信号进行激励。预失真实验表明,该方法能在保证模型精度的情况下大幅减少DPD模型系数和计算复杂度,为星载射频前端的预失真技术提供了有效的系数降维思路和方法。
-
关键词:
- 数字预失真 /
- 稀疏LSTSVR /
- Cholesky分解 /
- 功率放大器
Abstract: To compensate for the nonlinearity of the power amplifier in the RF front-end of high-capacity satellite communication, more coefficients and higher orders are required in the conventional Digital PreDistortion (DPD) model, which affects severely the resource consumption of the predistortion feedforward path. In this paper, a low-complexity DPD approach based on Improved Sparse Least Squares Twin Support Vector Regression (ISLSTSVR) modeling theory is presented to address this problem. Firstly, the problem that the solution of the Least Squares Twin Support Vector Regression(LSTSVR)model is not sparse is solved by constructing decision function in the original space; At the same time, the truncated least squares loss function is used to increase robustness of the model; Then the low-rank approximation of the kernel matrix is obtained by using Nystrom approximation method, and further Cholesky decomposition is used to reduce the operational complexity of the kernel matrix; Finally, the sparse solution of the model is obtained from low-rank kernel matrix. To verify the effectiveness of the proposed method, experiments are performed using a single-tube gallium nitride (GaN) broadband AB-class power amplifier with a 40 MHz 32 QAM signal for excitation. The experiment result shows that this method can greatly reduce the DPD model coefficients and computational complexity while ensuring the model accuracy, and provides an effective coefficient dimension reduction idea and method for the predistortion technology of the spaceborne RF front-end. -
表 1 不同样本集大小的机器学习模型建模效果对比
模型 样本数 训练时间(s) NMSE(dB) 模型系数 GMP 8000 0.63 –44.13 148 12000 0.73 –45.15 148 SVR 8000 1319.00 –46.29 7386 12000 2599.70 –48.02 11081 TSVR 8000 531.43 –46.91 7332 12000 2024.80 –47.61 10753 16000 5017.10 –47.89 14316 STSVR 8000 156.02 –47.27 2002 12000 456.54 –48.12 3002 16000 940.72 –48.98 4002 ISLSTSVR 8000 19.97 –47.23 788 12000 49.37 –48.19 874 16000 96.95 –48.92 940 表 2 不同模型预失真性能比较
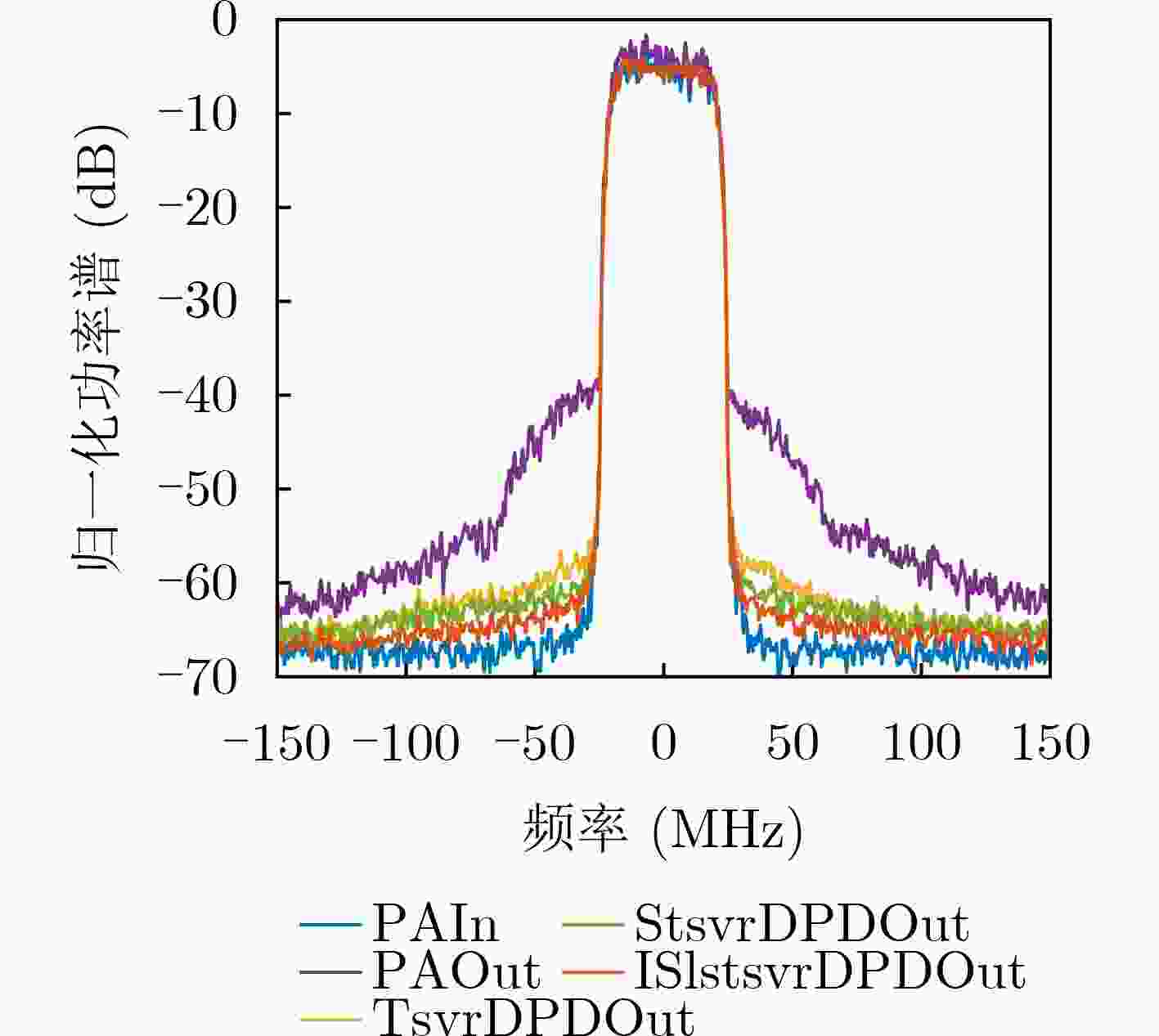
预失真器 ACPR(dB) –30 MHz +30 MHz 原始功放输出 –39.68 –41.23 TSVR预失真输出 –57.19 –57.20 STSVR预失真输出 –58.89 –58.95 ISLSTSVR预失真输出 –60.28 –61.00 -
[1] BEIDAS B F. Radio-frequency impairments compensation in ultra high-throughput satellite systems[J]. IEEE Transactions on Communications, 2019, 67(9): 6025–6038. doi: 10.1109/TCOMM.2019.2926031 [2] DOSHI R J, GHODGAONKAR D, BHARDHWAJ P S, et al. Accurate characterization of high power SSPA under multicarrier operation for satellite communications[C]. 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kerala, India, 2017: 818–823. [3] 黄明光, 朱丹, 何俊, 等. Ka波段宽频带高线性空间行波管研制[J]. 电子与信息学报, 2017, 39(11): 2777–2781. doi: 10.11999/JEIT161267HUANG Mingguang, ZHU Dan, HE Jun, et al. Development of Ka-band broadband, high-linearity space traveling wave tube[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2777–2781. doi: 10.11999/JEIT161267 [4] CHEN Wenhua, ZHANG Silong, LIU Youjiang, et al. Efficient pruning technique of memory polynomial models suitable for PA behavioral modeling and digital predistortion[J]. IEEE Transactions on Microwave Theory and Techniques, 2014, 62(10): 2290–2299. doi: 10.1109/TMTT.2014.2351779 [5] ABDELHAFIZ A, KWAN A, HAMMI O, et al. Digital predistortion of LTE-A power amplifiers using compressed-sampling-based unstructured pruning of Volterra series[J]. IEEE Transactions on Microwave Theory and Techniques, 2014, 62(11): 2583–2593. doi: 10.1109/TMTT.2014.2360845 [6] REINA-TOSINA J, ALLEGUE-MARTÍNEZ M, CRESPO-CADENAS C, et al. Behavioral modeling and predistortion of power amplifiers under sparsity hypothesis[J]. IEEE Transactions on Microwave Theory and Techniques, 2015, 63(2): 745–753. doi: 10.1109/TMTT.2014.2387852 [7] LI Mingyu, YANG Zhenxing, ZHANG Zhongming, et al. Sparsity adaptive estimation of memory polynomial based models for power amplifier behavioral modeling[J]. IEEE Microwave and Wireless Components Letters, 2016, 26(5): 370–372. doi: 10.1109/LMWC.2016.2549024 [8] BECERRA J A, MADERO-AYORA M J, REINA-TOSINA J, et al. A doubly orthogonal matching pursuit algorithm for sparse predistortion of power amplifiers[J]. IEEE Microwave and Wireless Components Letters, 2018, 28(8): 726–728. doi: 10.1109/LMWC.2018.2845947 [9] 赵辉, 莫谨荣, 王薇, 等. OFDM系统中基于压缩感知的非线性失真恢复研究[J]. 电子与信息学报, 2021, 43(7): 1907–1912. doi: 10.11999/JEIT200374ZHAO Hui, MO Jinrong, WANG Wei, et al. Research on nonlinear distortion recovery based on compressed sensing in OFDM system[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1907–1912. doi: 10.11999/JEIT200374 [10] BECERRA J A, MADERO-AYORA M J, REINA-TOSINA J, et al. A reduced-complexity doubly orthogonal matching pursuit algorithm for power amplifier sparse behavioral modeling[C]. 2019 IEEE Topical Conference on RF/Microwave Power Amplifiers for Radio and Wireless Applications (PAWR), Orlando, USA, 2019: 1–3. [11] BECERRA J A, AYORA M J M, REINA-TOSINA J, et al. Sparse identification of Volterra models for power amplifiers without pseudoinverse computation[J]. IEEE Transactions on Microwave Theory and Techniques, 2020, 68(11): 4570–4578. doi: 10.1109/TMTT.2020.3016967 [12] CRESPO-CADENAS C, MADERO-AYORA M J, BECERRA J A, et al. A fast sparse Bayesian pursuit approach for power amplifier linearization[C]. 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 2021: 1–3. [13] PENG Jun, HE Songbai, WANG Bingwen, et al. Digital predistortion for power amplifier based on sparse Bayesian learning[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2016, 63(9): 828–832. doi: 10.1109/TCSII.2016.2534718 [14] BECERRA J A, MADERO-AYORA M J, NOGUER R G, et al. On the optimum number of coefficients of sparse digital predistorters: A Bayesian approach[J]. IEEE Microwave and Wireless Components Letters, 2020, 30(12): 1117–1120. doi: 10.1109/LMWC.2020.3027878 [15] LIU Zhijun, HU Xin, WANG Weidong, et al. A joint PAPR reduction and digital predistortion based on real-valued neural networks for OFDM systems[J]. IEEE Transactions on Broadcasting, 2022, 68(1): 223–231. doi: 10.1109/TBC.2021.3132158 [16] WANG Zonghao, CHEN Wenhua, SU Gongzhe, et al. Low computational complexity digital predistortion based on direct learning with covariance matrix[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(11): 4274–4284. doi: 10.1109/TMTT.2017.2690290 [17] ZHANG Yikang, LI Gang, LI Hongmin, et al. Simplified vector decomposition time-delay neural network model for RF power amplifier modeling and digital predistortion[C]. 2021 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Nanjing, China, 2021: 1–3. [18] CAI Jialin, YU Chao, SUN Lingling, et al. Dynamic behavioral modeling of RF power amplifier based on time-delay support vector regression[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(2): 533–543. doi: 10.1109/TMTT.2018.2884414 [19] XU Jin, JIANG Weiliang, MA Linhua, et al. Augmented time-delay twin support vector regression-based behavioral modeling for digital predistortion of RF power amplifier[J]. IEEE Access, 2019, 7: 59832–59843. doi: 10.1109/ACCESS.2019.2915281 [20] CAI Tianfu, LI Mingyu, YAO Yao, et al. An improved nonlinear smooth twin support vector regression based-behavioral model for joint compensation of frequency-dependent transmitter nonlinearities[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2021, 31(6): e22636. doi: 10.1002/mmce.22636 [21] CHAPELLE O. Training a support vector machine in the primal[J]. Neural Computation, 2007, 19(5): 1155–1178. doi: 10.1162/neco.2007.19.5.1155 [22] SUYKENS J A K and VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293–300. doi: 10.1023/A:1018628609742 [23] CHEN Li and ZHOU Shuisheng. Sparse algorithm for robust LSSVM in primal space[J]. Neurocomputing, 2018, 275: 2880–2891. doi: 10.1016/j.neucom.2017.10.011 [24] ZHOU Shuisheng. Sparse LSSVM in primal using Cholesky factorization for large-scale problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(4): 783–795. doi: 10.1109/TNNLS.2015.2424684 -





 下载:
下载:


 下载:
下载:
