Digital Self-Interference Cancellation Based on Bounded Component Analysis for In-Band Full-Duplex
-
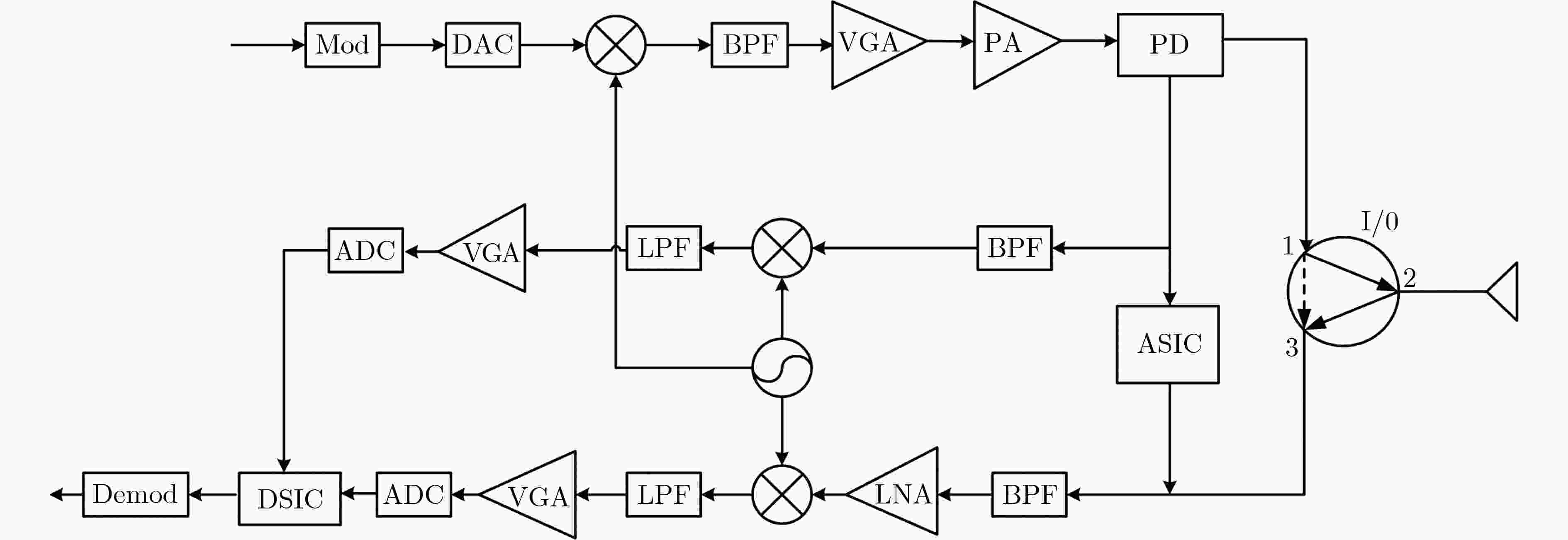
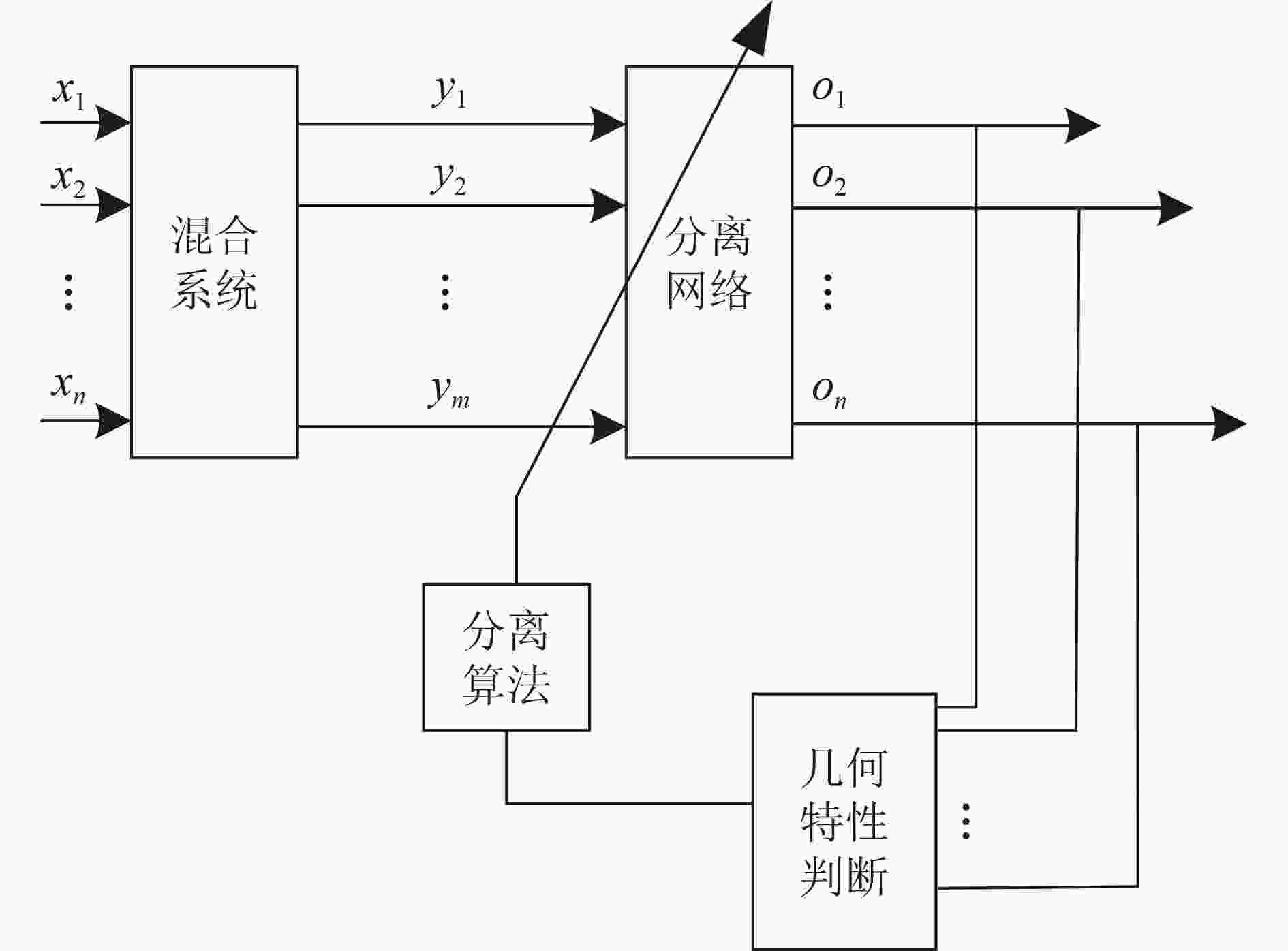
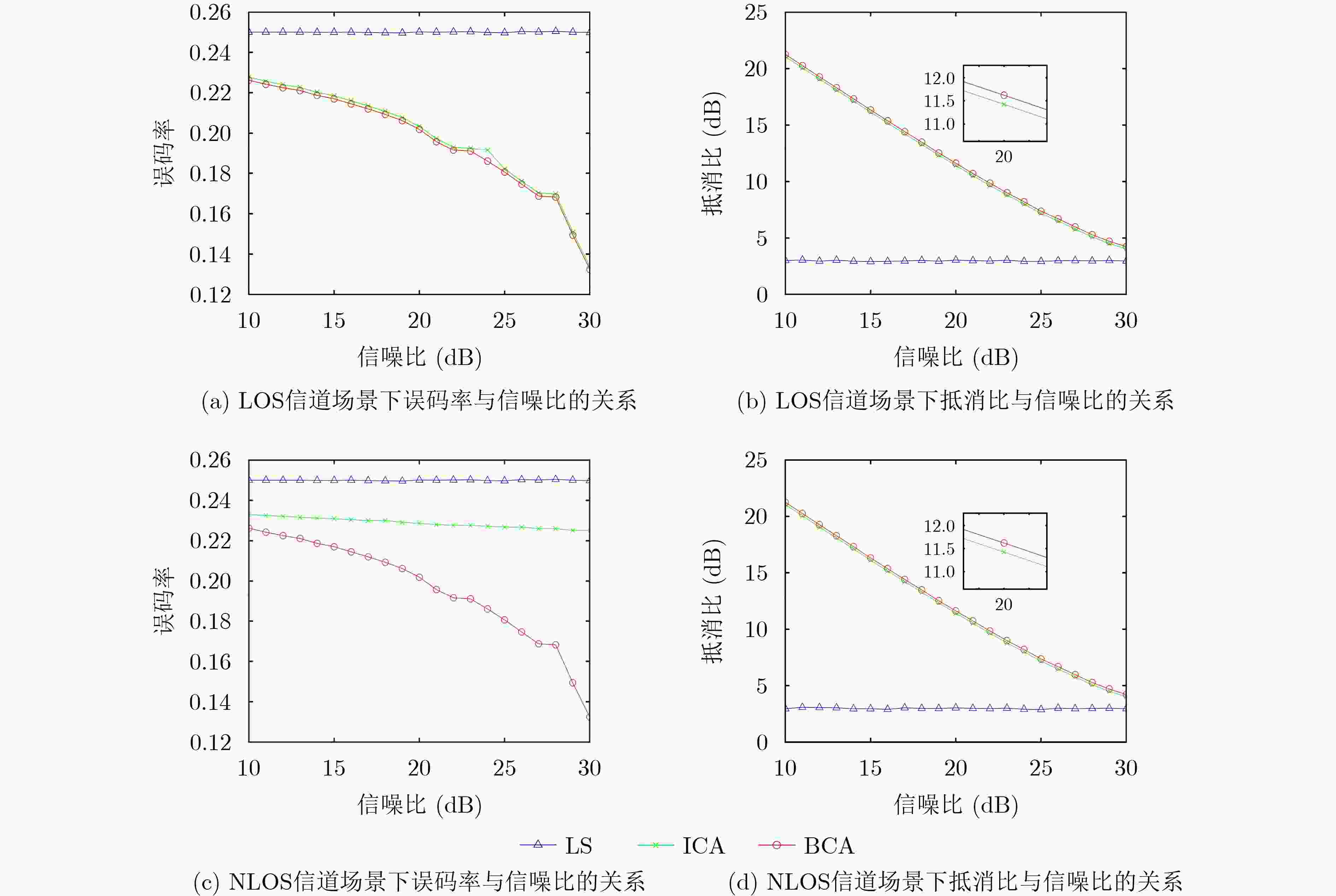
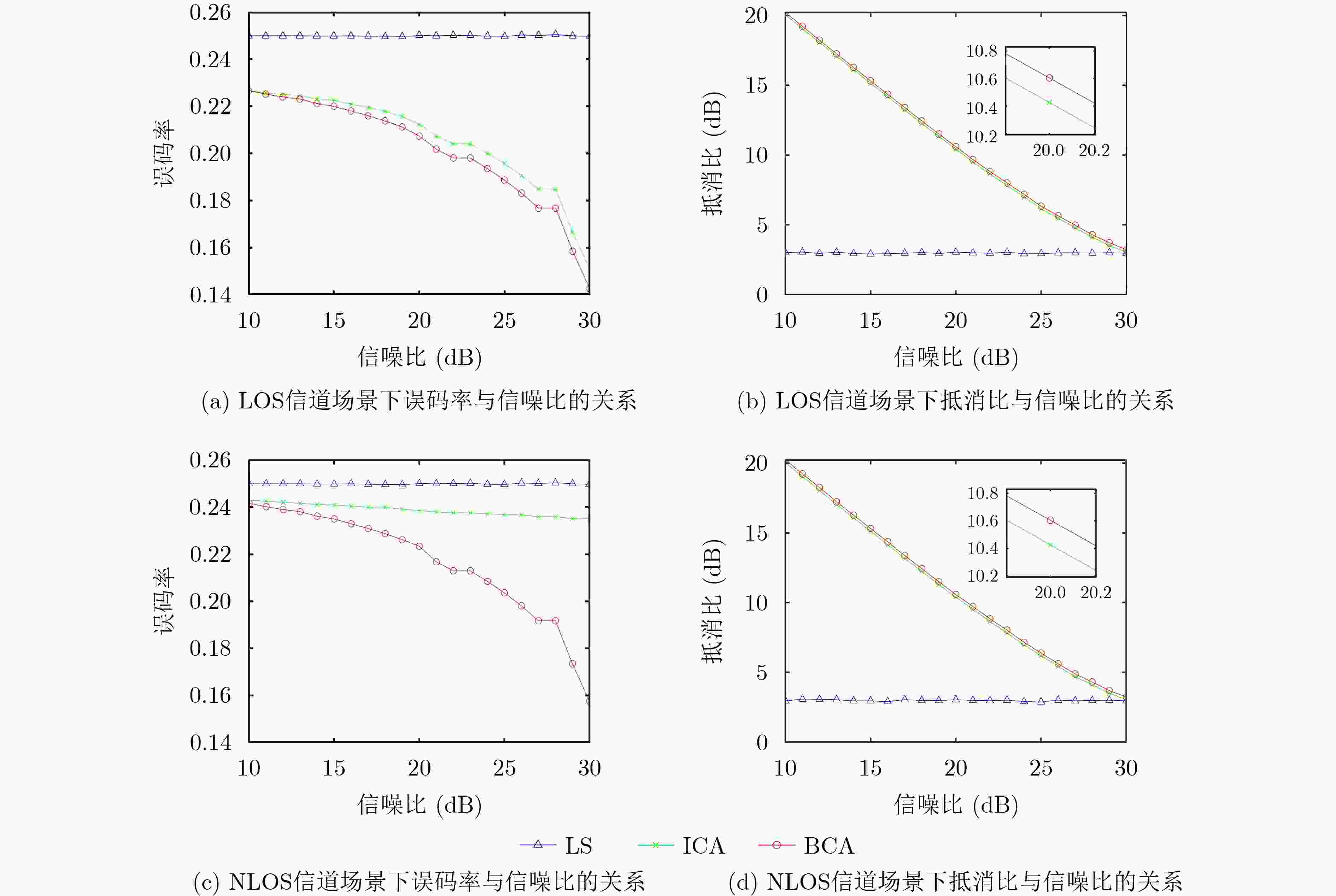
摘要: 凭借能够提升频谱利用率的优势,带内全双工(In-Band Full Duplex, IBFD)技术有望成为现代无线通信系统的潜在方案。然而,在应用过程中却面临自干扰抵消(Self-Interference Cancellation, SIC)的巨大挑战。SIC可以从空域、模拟域和数字域3个方面来单独或组合实现。该文重点研究了IBFD数字SIC。针对传统数字SIC性能受到收发链路器件非理想因素限制的问题,该文建立了一种射频辅助链路的IBFD系统,利用有用信号和自干扰信号的有界性,设计了一种基于有界成分分析的数字SIC方法。在视距(Line Of Sight, LOS)和非视距(Non-Line Of Sight, NLOS)两种信道场景下,利用仿真和实测数据进行了验证分析。结果表明,相比较于最小二乘方法和独立成分分析方法,所提有界成分分析方法改善了SIC效果,并提高了系统误码率性能。Abstract: In-Band Full Duplex (IBFD) technique is expected to be the most potential scheme for modern wireless communication system, since it can prove the spectral efficiency. However, in the application process, it faces the great challenge of Self-Interference Cancellation (SIC). SIC can be realized separately or in combination from three aspects: propagation domain, analog domain and digital domain. This paper focuses on digital SIC in the IBFD. To solve the problem that the performance of the traditional digital SIC is limited by the non-ideality of the components of transceiver link, this paper adopts an IBFD system of Radio Frequency (RF) auxiliary link. By exploiting the boundedness of signal of interest and self-interfering signal, a digital SIC algorithm based on bounded component analysis is developed. Under the two channel scenarios of the Line Of Sight (LOS) and the Non-Line Of Sight (NLOS), the simulation and measured data are used to verify and analyze. The results show that compared with the least square method and independent component analysis method, the proposed bounded component analysis method improves the SIC effect and improves the bit error rate performance of the system.
-
表 1 系统参数设置
系统参数 数值 自干扰噪声比(dB) 30 调制方式 QPSK 样本长度 1000 底部噪声功率(dBm) –90 仿真多径数 3 -
[1] 郝越凡. 同时同频全双工数字域深度学习自干扰抑制技术研究[D]. [硕士论文], 电子科技大学, 2020.HAO Yuefan. Full-duplex digital self-interference cancellation based on deep learning[D]. [Master dissertation], University of Electronic Science and Technology of China, 2020. [2] ERDEM M, GURBUZ O, and OZKAN H. A residual scheme for digital self-interference cancellation in full duplex communication[C]. 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 2020: 1–6. [3] XIE Mingcong, WEI Xizhang, TANG Yanqun, et al. A robust design for aperture-level simultaneous transmit and receive with digital phased array[J]. Sensors, 2022, 22(1): 109. doi: 10.3390/s22010109 [4] MOHAMMADIAN A, TELLAMBURA C, and VALKAMA M. Analysis of self-interference cancellation under phase noise, CFO, and IQ imbalance in GFDM full-duplex transceivers[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 700–713. doi: 10.1109/TVT.2019.2953623 [5] HE Meng and HUANG Chuan. Self-interference cancellation for full-duplex massive MIMO OFDM with single RF chain[J]. IEEE Wireless Communications Letters, 2020, 9(1): 26–29. doi: 10.1109/LWC.2019.2940433 [6] LEE D and MIN B W. Demonstration of self-interference antenna suppression and RF cancellation for full duplex MIMO communications[C]. 2020 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Seoul, Korea (South), 2020: 1–4. [7] AHMED E and ELTAWIL A M. All-digital self-interference cancellation technique for full-duplex systems[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3519–3532. doi: 10.1109/TWC.2015.2407876 [8] ADAMS M and BHARGAVA V K. Use of the recursive least squares filter for self interference channel estimation[C]. IEEE 84th Vehicular Technology Conference, Montréal, Canada, 2016: 1–4. [9] 董方亮. 同时收发系统中自干扰抑制算法研究[D]. [硕士论文], 西安电子科技大学, 2019.DONG Fangliang. Research on self-interference suppression algorithms in simultaneous transceiver system[D]. [Master dissertation], Xidian Universtioity, 2019. [10] CARDOSO J F. Blind signal separation: Statistical principles[J]. Proceedings of the IEEE, 1998, 86(10): 2009–2025. doi: 10.1109/5.720250 [11] LI Jiong, ZHANG Hang, and FAN Menglan. Digital self-interference cancellation based on independent component analysis for Co-time Co-frequency full-duplex communication systems[J]. IEEE Access, 2017, 5: 10222–10231. doi: 10.1109/ACCESS.2017.2712614 [12] CRUCES S, DURÁN I, SARMIENTO A, et al. Bounded component analysis of linear mixtures[C]. 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, USA, 2010: 1930–1933. [13] HUANGFU Yafan, LIU Youjiang, ZHANG Qi, et al. Nonlinear digital self-interference cancellation for full duplex systems in frequency agility mode[C]. 2019 IEEE 19th International Conference on Communication Technology, Xi'an, China, 2019: 16–19. [14] INAN H A and ERDOGAN A T. A bounded component analysis approach for the separation of convolutive mixtures of dependent and independent sources[C]. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013: 3223–3227. [15] 苏巧, 沈越泓, 徐鹏程. 有界混合信号的快速分离算法[J]. 计算机工程, 2016, 42(2): 86–92. doi: 10.3969/j.issn.1000-3428.2016.02.016SU Qiao, SHEN Yuehong, and XU Pengcheng. Fast separation algorithm for bounded mixed signals[J]. Computer Engineering, 2016, 42(2): 86–92. doi: 10.3969/j.issn.1000-3428.2016.02.016 -





 下载:
下载:


 下载:
下载:
